基于动态偏置分配PD-PWM的变桥臂换流器子单元电容均压策略
2016-08-30韦统振霍群海杨晓丹韩立博
朱 晋 韦统振 霍群海 杨晓丹 韩立博
(中国科学院电工研究所 北京 100190)
基于动态偏置分配PD-PWM的变桥臂换流器子单元电容均压策略
朱晋韦统振霍群海杨晓丹韩立博
(中国科学院电工研究所北京100190)
变桥臂多电平变流拓扑(A2MC)是一类采用全桥子单元级联结构和IGBT串联型导向开关结构相结合的新型多电平变流器拓扑。针对其全桥子单元级联结构电容电压均衡的问题,提出了一种新型简单有效的PD-PWM桥臂调制方法。与传统的调制策略相比,该调制方法更容易实现,具备更好的动态特性,并且大幅降低计算时间,该调制策略在各类全桥子单元级联结构中具备强可移植性。仿真和实验结果验证了这种新型调制策略的简单性和有效性。
全桥子单元变桥臂多载波调制策略动态载波偏置分配
0 引言
柔性直流输电技术(Voltoge Source Converter-High Voltage DC,VSC-HVDC)由于其特有的优势,引起了众多学者的广泛关注[1-3]。基于MMC结构的变流拓扑在世界上多个工程中得到了实际应用,各类文献也不断地提出了各种新型拓扑与控制策略[5-18]。
阿尔斯通公司提出的变桥臂多电平变流拓扑(Alternate-Arm Multi-Level Converter,A2MC)结构由于其独有的优势受到广泛关注[11,12],由于采用了独特的变桥臂变流方案,相对于半桥型模块化多电平换流器(Half bridge sub-Modular Multilevel Converter,H-MMC),其子单元数量最多可减少一半,在成本降低的同时,具备了直流侧故障隔离能力。文献[11,12]提出一种全桥变桥臂变流拓扑(Full-bridge Alternate-Arm Voltage Source Converter,FA2MC),如图1所示,该结构直流母线电压等级和子单元级联模块数量降为A2MC结构的一半,半桥型MMC(H-MMC)结构的四分之一,同时延续了变桥臂结构损耗低并且具备了直流侧故障隔离能力的优势。
目前,已有较多文献针对MMC结构控制策略进行了广泛的研究,对变桥臂拓扑结构的调制策略设计具有一定的参考性。文献[13]采用了载波移相控制策略,然而当这种策略应用于多子单元结构时,为了平衡子单元电容电压,每个子单元需要独立的PI模块控制其参考波电压偏置。当子模块数较多时,将大大增加控制系统的复杂度[14]。并且由于无法使每相子单元数量保持为n,导致各相环流较大,需要增加缓冲电感[15]。文献[16,17]采用了预测控制策略,能够在保证子单元电压均衡的同时有效抑制环流,但是由于预测控制计算量较大,不适用于子单元数量成百上千的直流输电变电站。文献[18-20]采用了阶梯波调制方法,以及改进的电平逼近调制策略,控制策略较为简单,但是大量子单元电容电压排序问题大幅增大了控制器的负担,成为了一个亟待解决的问题。
文献[21]提出一种循环分配载波偏置的多载波(Phase-Disposition Pulse Width Modulation,PD-PWM)调制策略,能够在对称稳态条件下均衡各子单元电压,但是不具备容错机制和快速纠错能力。文献[22]提出一种基于选择性循环多载波调制策略,充分利用FPGA并行计算的优点,大幅节省了CPU计算时间,从而减少了控制延迟误差。然而文献[22]提出的调制策略仅适用于半桥子单元的MMC结构。当这种单参考波的调制策略应用于基于H全桥子单元的变桥臂模块化多电平结构时,每个全桥子单元仅能输出+Vc和-Vc两种电平,缺少了输出0电平的自由度,使得整个级联阀组输出电平数少,控制自由度降低,输出交流谐波含量大。
与文献[22]中用于半桥型MMC的调制策略相比,本文在FA2MC结构基本阀控策略的基础上,重点分析了单极性多载波全桥子单元级联结构的子单元电容电压波动规律与载波分配关系。既能充分利用了全桥子单元输出三个自由度的优点,使输出电压电平数更多,又能在各电容参数不对称的情况下也同样具备子单元电容电压均衡能力和较强的抗干扰能力。并以文献[11,12]中所提出的全桥型变桥臂拓扑为对象,系统阐述了该调制策略的原理,仿真与实验结果验证了该调制策略的简单高效。
1 FA2MC结构与工作原理
图1a所示的系统单相变流拓扑主要分为三部分:级联阀组部分、缓冲电感和波形导向部分。

图1 FA2MC单相变流原理图Fig.1 Single phase converter of FA2MC
当图1中的拓扑结构输出正弦交流电压时,其波形导向部分S1~S4开关组合两端需要输出如图2所示的Uds电压波形,表达式为
(1)
式中,Uds为正弦半波波形,然后通过S1~S4的导向作用,使交流侧输出正弦波形,S1~S4开通关断均处于零电压环境,并且切换频率为100 Hz,有效降低开关损耗。忽略缓冲电感上的压降,则级联阀组部分Ucs输出电压波形表达式为
(2)
其波形如图2c所示。根据文献[26]中的推导,桥臂上的级联阀组每半个周期内的能量是否平衡与流过级联阀组的电流无关,只需要Udc与Uac满足
(3)
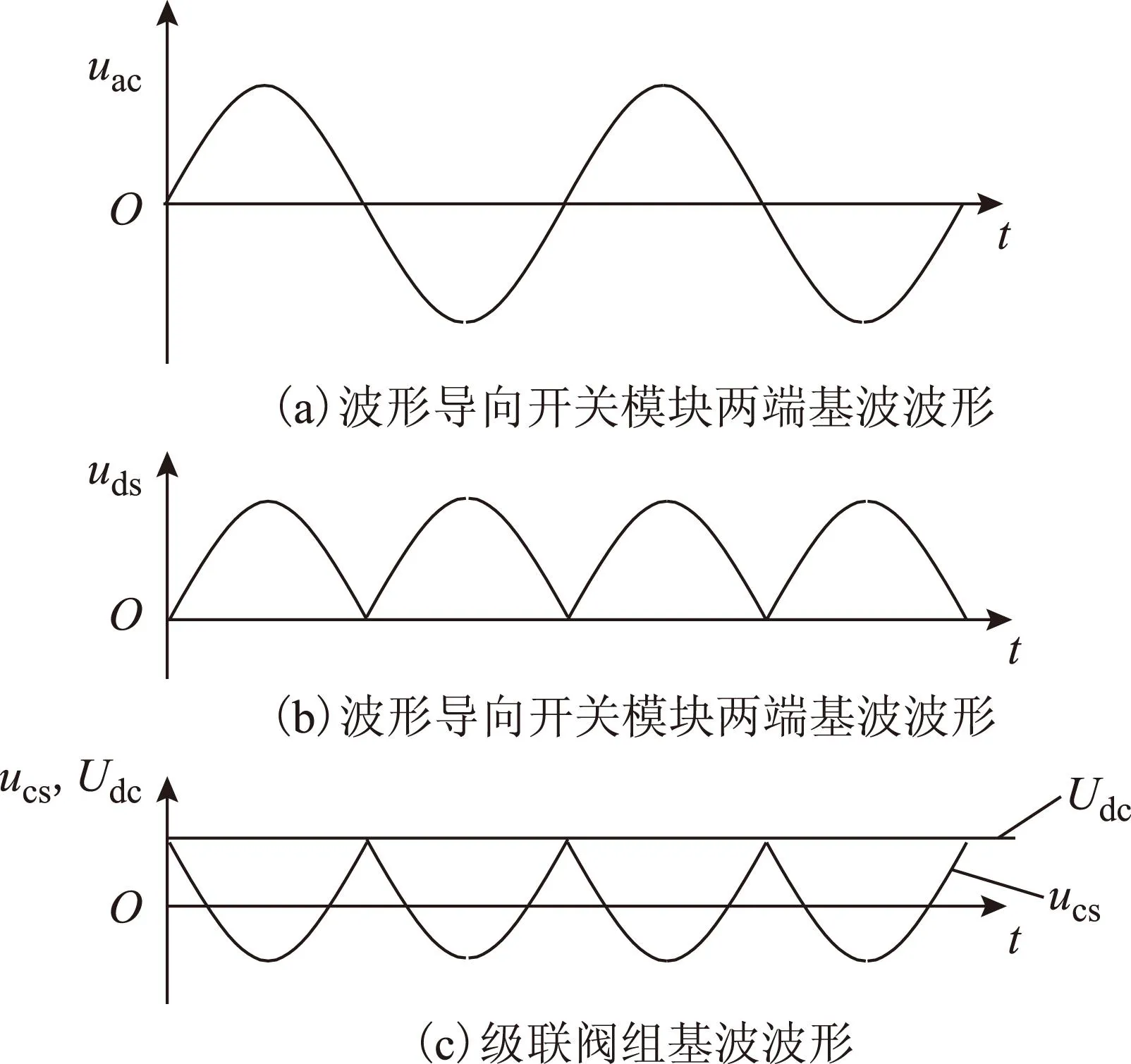
图2 单相逆变拓扑输出交流电压时对应波形Fig.2 Waveforms of single phase inverter
2 选择性排序多载波调制策略
2.1基于传统多载波PD-PWM的调制策略
根据上述工作原理,为了充分利用全桥子单元的三种输出电平优势,本文采用类似单极性级联型PWM调制方法中的双参考波产生策略。
在桥臂接收到变流站站控核心控制器输出的单相交流电压指令后,根据第1节的工作原理,如果逆变输出正弦交流电压,桥臂级联阀组就应该输出如图2c中所示电压波形,因此,桥臂级联阀组的两组调制波utz1、utz2与站控核心控制单元输出的交流电压Uac指令关系如图3所示。调制波1与调制波2的表达式为
(4)
(5)
式中,Umax为多载波中偏置最大的载波波动峰值;Umin为多载波中偏置最小的载波波动谷值,上述表达式将根据Udc与uac计算出的双调制波波动范围与多载波波动范围相匹配。
双调制波多载波调制方法的工作原理如下:
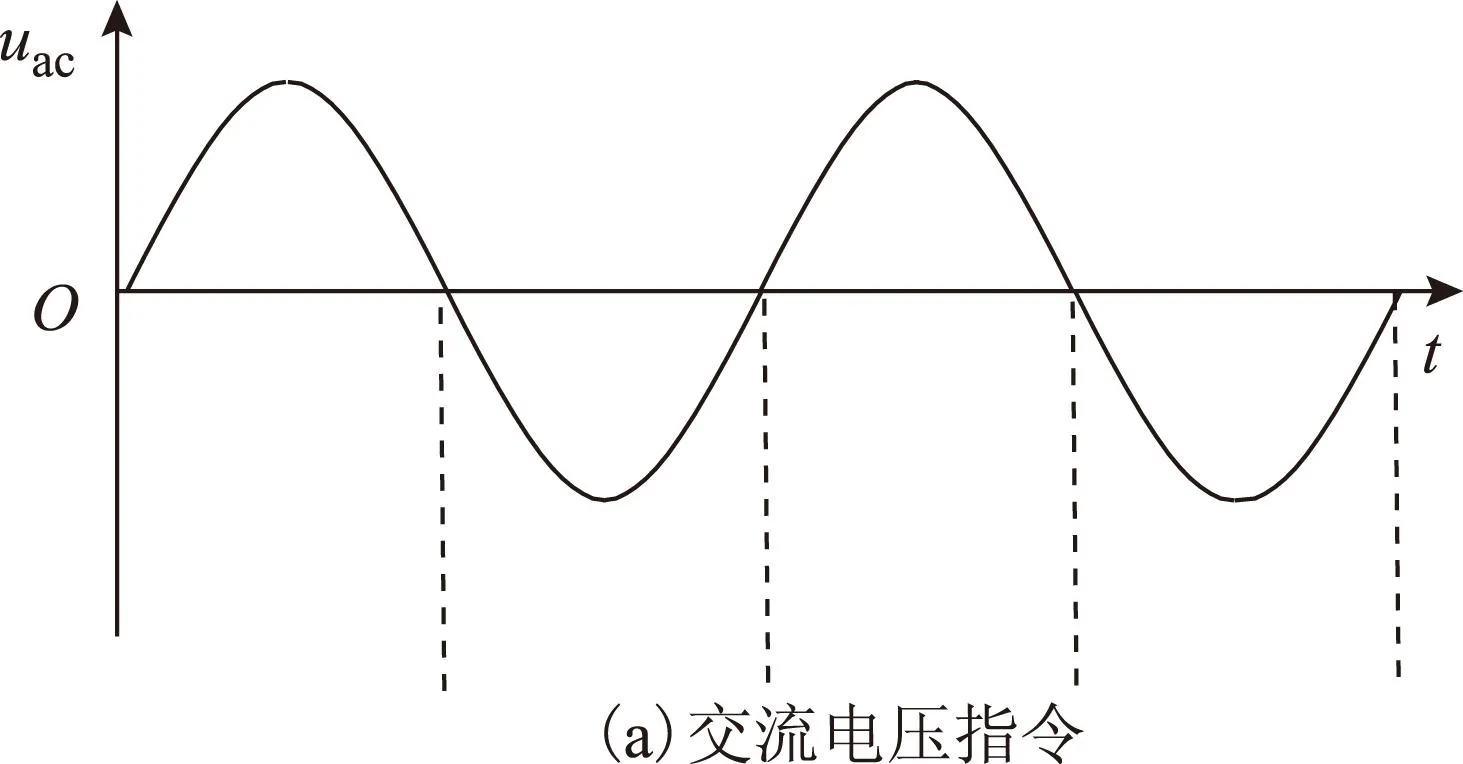
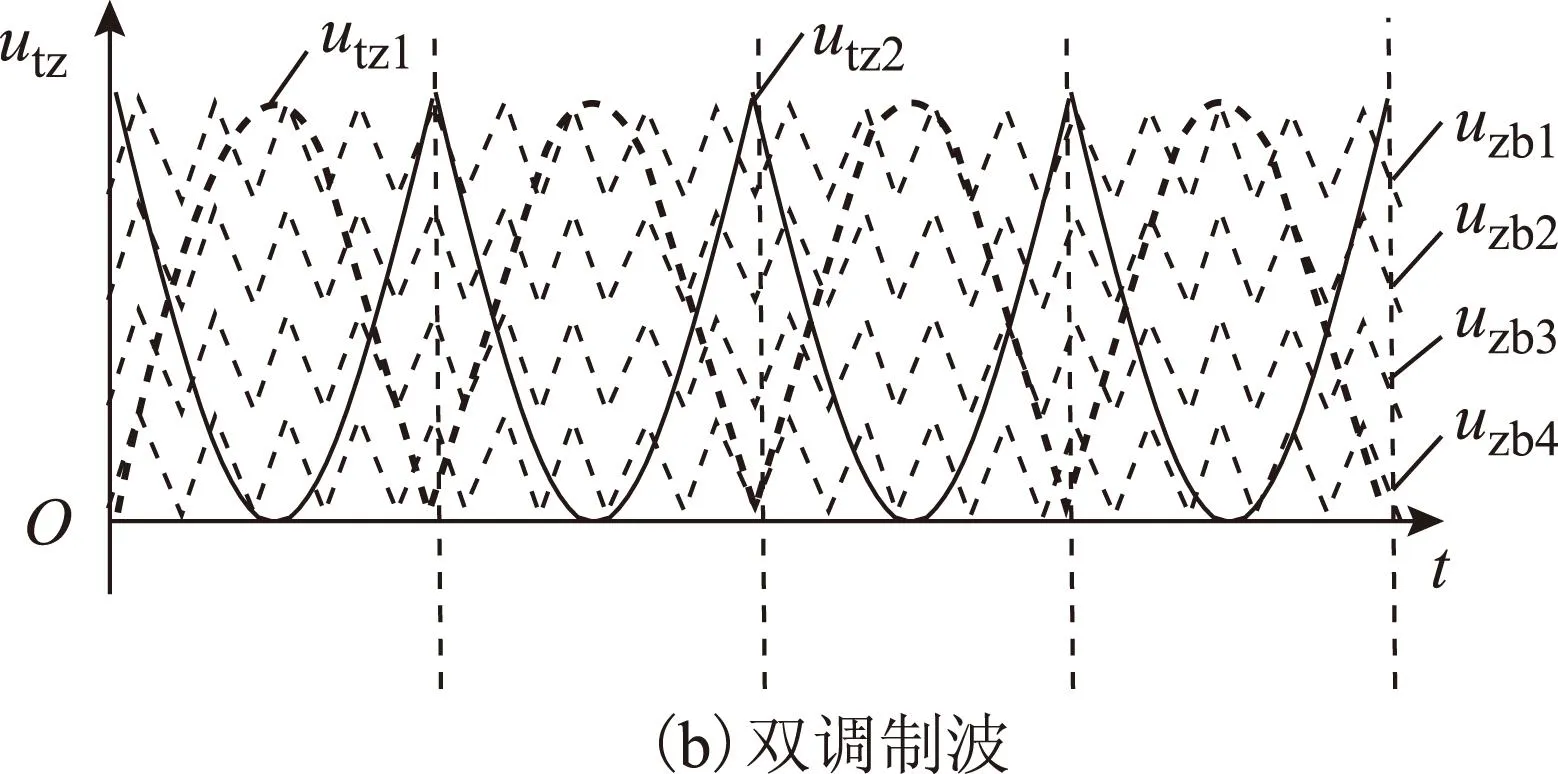
图3 交流电压参考指令与级联阀组双参考波Fig.3 Reference voltage of AC side and cascade valve group
以子单元1对应的载波1为例进行说明,其输出电平与调制策略的关系见表1。

表1 子单元输出电平Tab.1 Output level of SM
上述双调制波策略能够在采用PD-PWM多载波的同时,充分发挥H全桥子模块三个电平输出自由度的优势,并且无需每个周期计算输出零电平的子单元数。但是如何引入子单元电容电压均衡策略是模块化多电平变流拓扑采用PD-PWM时的一大难点。
如图3b和表1所示,由于各子单元对应载波位置的固定及其偏置量的不同,导致各子单元在一个调制波周期内接入电路充放电的时间必然不等。因此造成了各子单元电容电压的不均等,这也是传统多载波PD-PWM调制策略通常仅适用于具备独立直流电源的全桥结构的原因。
2.2基于循环载波偏置PD-PWM的调制策略
与传统多载波PD-PWM相比,循环载波偏置PD-PWM在每个载波周期开始时对各子单元载波偏置进行变更。如图4所示,子单元1对应载波(zb1)第一载波周期时偏置为0,第二载波周期时偏置为2,以此类推。当频率足够高时,这种调制策略能够使一个周期内充放电功率在各子单元尽可能均分。但是,由于其分配策略和循环方式已经固定,该调制方法并不具备根据子单元电容电压实时情况调整功率分配的能力,因此也无法对子单元电容电压实现动态闭环均衡,同时也无法适用于当子单元电容参数存在差异的实际工况。
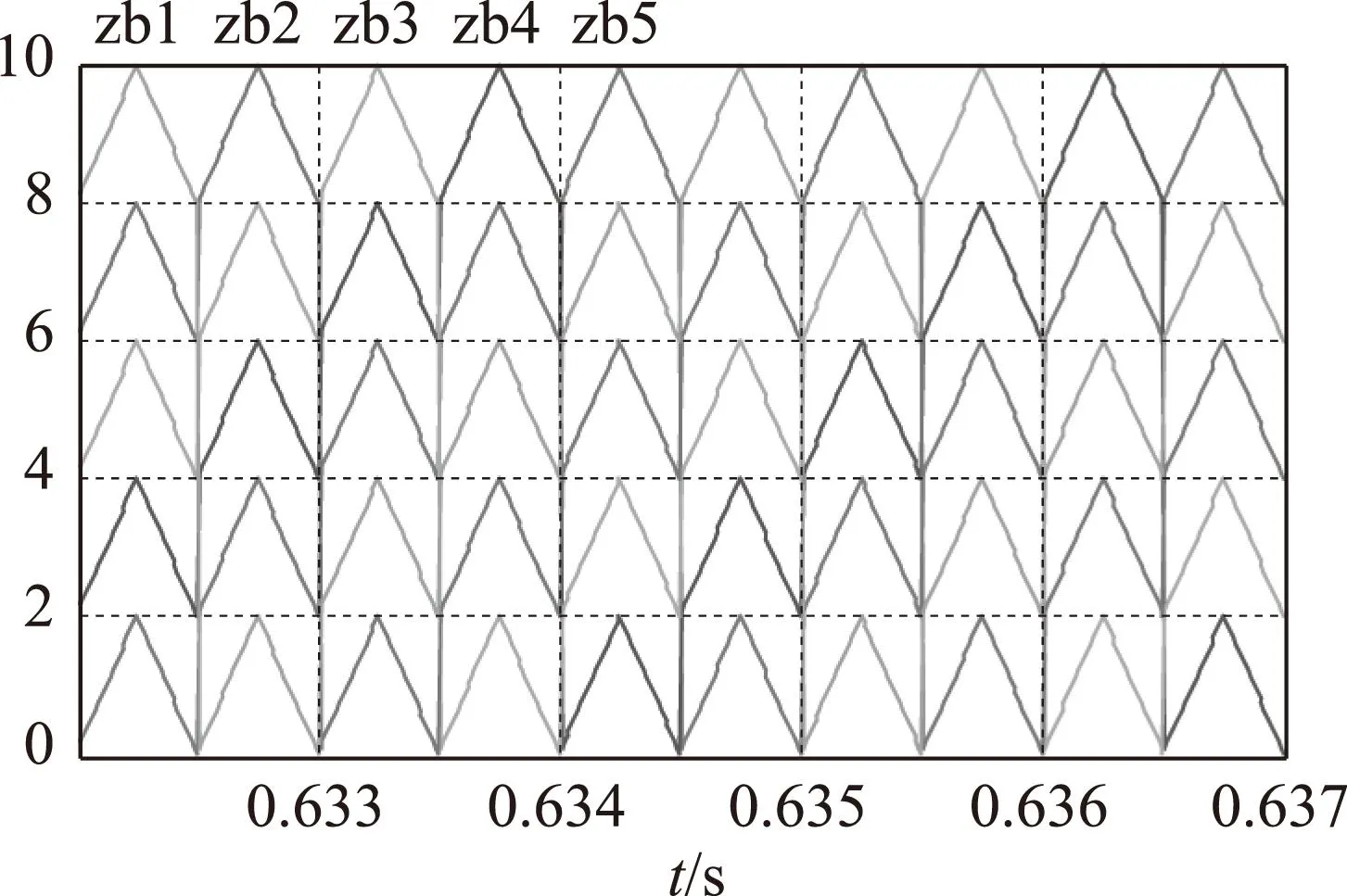
图4 循环载波偏置PD-PWM载波分配示意图Fig.4 Schematic diagram of PD-PWM carrier allocation for cyclic carrier offset
2.3动态载波偏置型PD-PWM调制策略
假设调制比为1,采用上一小节的双调制波产生方法之后,产生了tz1和tz2两路调制信号如图5所示。在半个交流周期中,根据两组调制波的大小将其按照时间刻度分为两个部分:区域1和区域2。

图5 半个周期内载波调制波坐标图区域划分Fig.5 Region division of the carrier modulated wave in half cycle
图5的区域1中,utz1
本文中阀组级联子单元数量为5,因此将纵坐标分为Ⅰ-Ⅳ五个区间。叠加了bias 1信号的三角载波在纵坐标Ⅰ区间波动,叠加了bias 2信号的三角载波在纵坐标Ⅱ区间波动,以此类推。
根据表1所述的调制方法,各子单元调制真值表与调制波tz1落在的区域关系见表2。

表2 各载波偏置对应子单元输出开关信号Tab.2 Output switching signal of corresponding carrier offset of each SM output switching signal
例如区域1中,tz1落在I时,bias 1对应子单元输出真值表为-1与0之间变化的PWM波(-P1),bias 2~bias 4对应子单元输出-1,bias 5对应子单元输出真值表为0到-1之间变化的PWM波(-P5)。
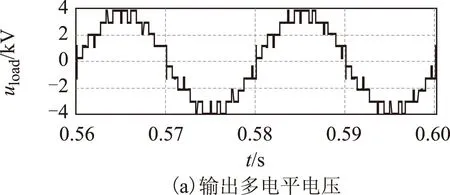
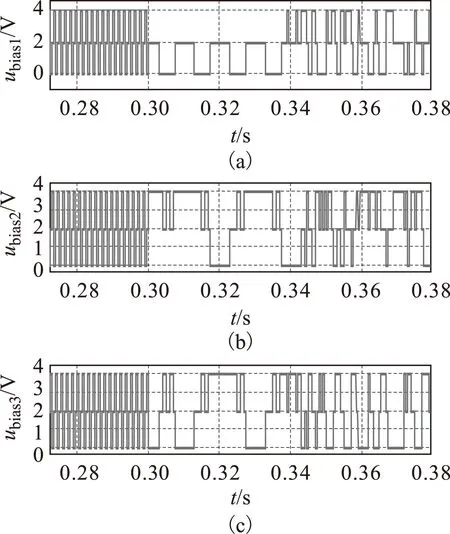
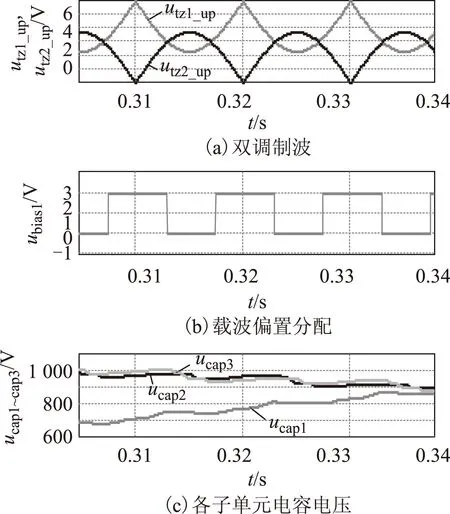
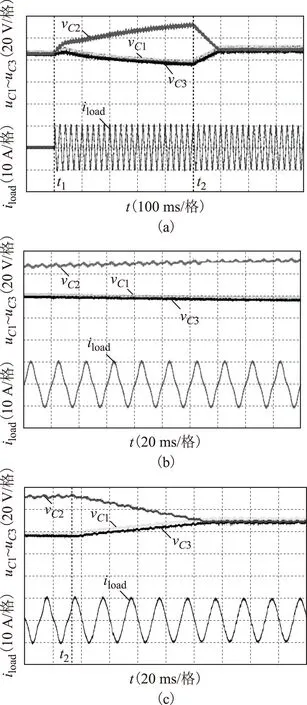
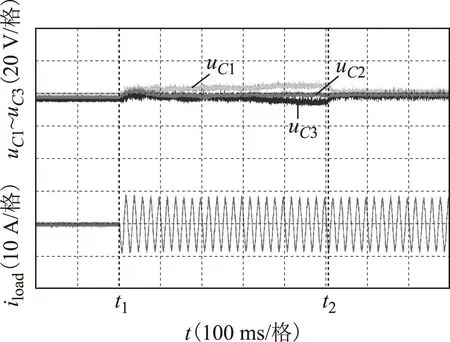
根据表3所示,在区域1中,即utz1 在区域2中,即utz2 根据上述规律,结合电流方向,以子单元电容电压充点或放电时间长短可将阀组划分为以下两种工况。 表3 工况分类Tab.3 Classification of working conditions 根据表3中的工况划分,在每一个三角载波周期,可以采用以下步骤计算各子单元所应该叠加的偏置信号: (1)通过FPGA并行计算,选择当前时刻最大子单元电容电压和最小子单元电容电压。 (2)根据当前实时检测的电流和上级控制器(直流输电变流站站控系统)给出的调制信号,以及本文2.1节所述的双调制波产生方法,判断此时阀组处于表3中的哪种工况。 若处于工况Ⅰ,将最小电容电压对应子单元的载波信号叠加bias 3偏置信号。将最大电容电压对应子单元载波信号叠加bias 1或bias 5信号。其余子单元载波与其余偏置信号一一对应,或按照文献[21]中的LSM策略循环分配偏置信号,组成图3所示的层叠多载波。 若处于工况Ⅱ,将最大电容电压对应子单元的载波信号叠加bias 3偏置信号。将最小电容电压对应子单元载波信号叠加bias 1或bias 5信号。其余子单元载波与其余偏置信号一一对应,或按照文献[21]中的LSM策略循环分配偏置信号,组成图4所示的层叠多载波。整个阀组各子单元对应载波产生办法与调制波产生策略框图如图6所示。 图6 调制策略总原理框图Fig.6 General principle block diagram of modulation strategy 本文在电磁暂态仿真软件PSIM中搭建了FA2MC变流拓扑的单相逆变模型,根据式(3)确定调制比,根据文献[12]中推导的子单元电容参数选择依据,选择电容值,仿真参数见表4所示。 表4 仿真参数表Tab.4 Simulation parameters 载波频率的选择对均压效果有显著影响,然而,载波频率升高将直接导致IGBT开关频率升高,导致装置损耗增大。本文在相同的载波频率下,对几种类型的PD-PWM进行了仿真和实验对比,各类载波偏置分配方法频率均设置为2 kHz。 三个载波波动范围分别为0~2,2~4,4~6,因此各载波对应的偏置量应该设为表5所示值。 表5 仿真中各载波偏置信号对应的偏置值Tab.5 The offset value of each carrier signal in simulation 为了测试本文所述方法的动态电压均衡特性,本文在子单元1的两端并联了100 Ω的电阻,在仿真的前0.3 s首先采用了类似文献[21]中所述的LSM循环分配偏置策略,0.3 s时切换至本文所述的调制策略,图7为仿真结果。图7a为各个子单元电容电压波形,图7b和图7c为切换前后的逆变器输出电流波形。 图7 从LSM策略切换至本文所述调制策略前后各点电压电流波形Fig.7 Voltage and current waveform before and after the switching from LSM to the proposed modulation strategy 由图7a可以看出,循环多载波控制策略无法满足这种各子单元电容参数差异较大时的均衡需求,各子单元电容电压偏差较大,在0.3 s切换至本文所述的控制策略时,各子单元电容电压在0.05 s内迅速趋于相当,并最终都在给定值1 000 V左右波动。图7b和图7c显示输出电压电流波形在本文所述调制方法作用下受到子单元电压波动影响较小,图8为变流器输出电压波形的放大图。 图8 0.4 s之后输出电压电流放大波形Fig.8 Output voltage and current waveform after 0.4 s 图9 0.3 s子单元1投入并联电阻时,各子单元载波偏置分配值变化波形Fig.9 The distribution value of the carrier offset of each SM when the resistance of SM1 is connected in 0.3 s 图10 0.3 s子单元1投入并联电阻时,各子单元输出PWM电压波形Fig.10 The PWM output voltage of each SM when the resistance of SM1 is connected in 0.3 s 图9为并联电阻10 Ω时,各子单元载波偏置分配情况,图10为对应的子单元电容输出PWM电压。与文献中的规律循环偏置配置方法以及传统的恒定偏置配置型PD、PWM不同,本文所述的方法在每个载波周期起始时刻根据上述小节中的区域划分和电容电压Min/Max原则灵活分配载波偏置。 图11所示为并联10 Ω电压导致子单元1电容电压跌落为三个子单元的最小值,此时子单元1载波偏置分配状况,以及对应的调制波某时刻放大波形,由于此时负载情况接近纯阻性负载,阀组电流持续为正,因此在utz1>utz2时,子单元1的载波偏置(bias 1)持续分配为2(表5中的bias 2);utz2>utz1,子单元1的载波偏置(bias 1)持续分配为0(表5中的bias 1)。与本文理论分析所述相同,每个周期达到了最大限度地对子单元1进行充电和放电时间为0,整个算法执行简单有效。 图11 子单元1载波偏置分配放大情况Fig.11 The distribution of carrier bias of SM1 在仿真验证之后,搭建了基于该拓扑结构三子单元单相小型样机逆变实验平台。实验结果如图12所示,图12中,vC1~vC3是三个子单元的电容电压波形,iload是负载电流波形。在图12中的t1时刻之前,实验平台闭锁,子单元电容被预充电至40 V。在t1时刻解除实验平台的闭锁状态,使逆变实验平台开始运行,t1~t2时间段内采用传统PD-PWM调制策略,如图12a所示,由于传统PD-PWM调制策略特性,子单元悬浮电容电压越来越不平衡,图12b为子单元电容不平衡时的子单元电容电压和负载电流放大波形,由图12b可以看出,当子单元电容不平衡时,负载电流波形同时会受到严重影响。图12c为t1时刻之后采用本文所提出的改进型PD-PWM调制策略后的放大波形,随着子单元电容电压被迅速均衡,输出电流波形也随之改善。 图12 传统PD-PWM与本文PD-PWM实验波形对比Fig.12 Comparison of experimental waveforms between traditional PD-PWM and PD-PWM proposed in this paper 在与传统PD-PWM调制策略进行对比之后,在调制波频率为2 kHz时,将这种调制策略与循环PD-PWM调制策略进行了比较实验,实验结果如图13所示,在t1时刻解除实验平台闭锁,t1~t2时刻采用循环载波偏置分配PD-PWM调制策略,在t2时刻以后采用本文所提出的改进型PD-PWM调制策略。对比图12a与图13中t1~t2时刻,采用循环载波偏置分配PD-PWM调制策略时子单元电容电压的不平衡情况比采用传统PD-PWM调制策略时明显减小,但是依然存在不平衡情况,这是因为载波频率为2 kHz时,各自单元电容采用循环载波分配策略时并不能完全做到功率的均衡分配,此外,电容的细微参数差异也会导致不均衡情况的出现。t2时刻启动本文的调制策略,子单元电容电压严格平衡。上述两个实验有效证明了本文所提改进型PD-PWM调制策略的可行性,以及与其他类型PD-PWM调制策略相比的优越性。 图13 载波频率为2 kHz时,循环偏置分配型PD-PWM与本文PD-PWM实验波形对比Fig.13 When the carrier frequency is 2 kHz,comparison of experimental waveforms between the distribution cyclic bias PD-PWM and the PD-PWM proposed in this paper 本文首先讨论了当前各种多电平调制策略在全桥子单元变桥臂变流拓扑中应用面临的问题,在PDPWM调制策略的基础上,提出一种基于调制波区域划分的多载波偏置选择性分配方法。该调制策略在最大限度发挥全桥子单元多电平自由度,低谐波输出电压优势的同时,能够有效均衡各子单元电容电压,且有效降低了阀组控制器的运算负担,易于工程实现。仿真与实验结果验证了该调制策略的有效性与可行性。 [1]胡鹏飞,江道灼,郭捷,等.基于混合型多电平换流器的柔性直流输电系统[J].电力系统保护与控制,2013,41(10):33-38. Hu Pengfei,Jiang Daozhuo,Guo Jie,et al.VSC-HVDC system based on hybrid multilevel voltage sourced converters[J].Power System Protection and Control,2013,41(10):33-38. [2]孙晓云,同向前,高鑫.柔性直流输电系统中IGBT阀的故障诊断方法[J].电工技术学报,2014,29(8):235-241,264. Sun Xiaoyun,Tong Xiangqian,Gao Xin.Research on the fault diagnosis of IGBT valve in VSC-HVDC[J].Transactions of China Electrotechnical Society,2014,29(8):235-241,264. [3]涂小刚,罗海云,程晓绚,等.多端柔性直流输电工程控保系统接口设计[J].电力系统保护与控制,2015,43(5):124-128. Tu Xiaogang,Luo Haiyun,Cheng Xiaoxuan,et al.Control and protection system interface design for multi-terminal HVDC flexible project[J].Power System Protection and Control,2015,43(5):124-128. [4]楚遵方,李耀华,王平,等.柔性直流输电系统中模块化多电平变流器的直流侧充电策略分析[J].电工技术学报,2015,30(12):136-142. Chu Zunfang,Li Yaohua,Wang Ping,et al.Analysis of charging strategy by dc grid of modular multilevel converter in high voltage direct current transmission system[J].Transactions of China Electrotechnical Society,2015,30(12):136-142. [5]范心明,管霖,何健明,等.风电接入下柔性直流输电的无源解耦控制[J].电工技术学报,2013,28(10):311-319. Fan Xinming,Guan Lin,He Jianming,et al.Decoupling passivity control of VSC-HVDC connected wind power[J].Transactions of China Electrotechnical Society,2013,28(10):311-319. [6]李爽,王志新,王国强.海上风电柔性直流输电变流器P-DPC控制研究[J].电工技术学报,2013,28(2):264-270. Li Shuang,Wang Zhixin,Wang Guoqiang.Predictive direct power control strategy for offshore wind power VSC-HVDC converter[J].Transactions of China Electrotechnical Society,2013,28(2):264-270. [7]Debnath S,Saeedifard M.A new hybrid modular multilevel converter for grid connection of large wind turbines[J].IEEE Transactions on Sustainable Energy,2013,4 (4):1051-1064. [8]Feldman R,Tomasini M,Amankwah E,et al.A hybrid modular multilevel voltage source converter for HVDC power transmission[J].IEEE Transactions on Industry Applications,2013,49 (4):1577-1588. [9]Fujin D,Zhe C.A control method for voltage balancing in modular multilevel converters[J].IEEE Transactions on Power Electronics,2014,29(1):66-76. [10]Jiangchao Q,Saeedifard M.Reduced switching-frequency voltage-balancing strategies for modular multilevel HVDC converters[J].IEEE Transactions on Power Delivery,2013,28 (4):2403-2410. [11]朱晋,韦统振,霍群海.一种新型全桥变桥臂型VSC-HVDC变流拓扑[J].中国电机工程学报,2013,33(3):52-61. Zhu Jin,Wei Tongzhen,Huo Qunhai.A new full-bridge alternative arm based VSC-HVDC converter[J].Proceedings of the CSEE,2013,33(3):52-61. [12]朱晋,韦统振,李东,等.全桥变桥臂电压源变流器拓扑参数及恒压策略研究[J].中国电机工程学报,2013,33(21):26-35. Zhu Jin,Wei Tongzhen,Li Dong,et al.A parameter and voltage balancing scheme for full-bridge alternate arm voltage source converters[J].Proceedings of the CSEE,2013,33(21):26-35. [13]Hagiwara M,Nishimura K,Akagi H.A medium-voltage motor drive with a modular multilevel PWM inverter[J].IEEE Transactions on Power Electronics,2010,25(7):1786-1799. [14]Wang Kui,Li Yongdong,Zheng Zedong,et al.Voltage balancing and fluctuation-suppression methods of floating capacitors in a new modular multilevel converter[J].IEEE Transactions on Industrial Electronics,2013,60 (5):1943-1954. [15]Li Zixin,Wang Ping,Zhu Haibin,et al.An improved pulse width modulation method for chopper-cell-based modular multilevel converters[J].IEEE Transactions on Power Electronics,2012,27 (8):3472-3781. [16]Perez M A,Rodriguez J,Fuentes E J,et al.Predictive control of AC-AC modular multilevel converters[J].IEEE Transactions on Industrial Electronics,2012,59 (7):2832-2839. [17]Qin jiangchao,saeedifard M.Predictive control of a modular multilevel converter for a back-to-back HVDC system[J].IEEE Transactions on Power Delivery,2012,27(3):1538-1547. [18]Guan M,Xu Z.Optimized capacitor voltage balancing control for modular multilevel converter based VSC-HVDC system[J].Proceedings of the CSEE,2011,31(12):9-14. [19]Rohner S,Bernet S,Hiller M,et al.Modulation,losses,and semiconductor requirements of modular multilevel converters[J].IEEE Transactions on Industrial Electronics,2010,57(8):2633-2642. [20]Wang K,Li Y,Zheng Z,et al.Voltage balancing and fluctuation suppression method of floating capacitors in a new modular multilevel converter[J].IEEE Transactions on Industrial Electronics,2013,60(5):1943-1954. [21]Sedghi S,Dastfan A,Ahmadyfard A.A new multilevel carrier based pulse width modulation method for modular multilevel inverter[C]//Proceedings of ICPE/ECCE,Jeju,Korea,2011:1432-1439. [22]Jun M,Ke S,Bailu X,et al.A new selective loop bias mapping phase disposition PWM with dynamic voltage balance capability for modular multilevel converter[J].IEEE Transactions on Industrial Electronics,2014,61 (2):798-807. A Dynamic Bias Distribution PD-PWM Strategy for Alternate Arm Modular Multilevel Converter Zhu JinWei TongzhenHuo QunhaiYang XiaodanHan Libo (The Institute of Electrical EngineeringChinese Academy of SciencesBeijing100190China) Alternate arm multilevel converter (A2MC) is a new voltage source converter topology which is suitable for high voltage direct current transmission(VSC-HVDC).This paper presents an improved phase disposition pulse width modulation suited for full-bridge cells in this topology.Compared to conventional carrier phase-shifted PWM,this modulation method is more easily to be realized and increase the robustness of system,the computation burden is also reduced.This method can be transfer to any other full bridge cells cascaded structure.Simulation and experimental results demonstrate the simplicity and effectiveness of this new type of modulation strategy. Full-bridge sub-module,alternate-arm voltage source converter,novel PD-PWM strategy,dynamic bias distribution 2014-12-17改稿日期2015-08-25 TM46 朱晋男,1987年生,博士研究生,主要从事大功率电力电子装置在电力系统中的应用研究。 E-mail:zhujin@mail.iee.ac.cn 韦统振男,1976年生,研究员,研究方向为定制电力技术、电能质量分析和治理、超级电容器储能系统和应用、高压大功率变流器以及直流固态断路器。 E-mail:tzwei@mail.iee.ac.cn(通信作者)

3 仿真与实验





4 结论
