基于改进差分进化算法的潮流发电机组微观选址

王丛佼　王锡淮　陈国初　陈建民　陈　晶

(1.上海海事大学物流工程学院　上海　201306 2.上海电机学院电气学院　上海　200240 3.中国石油大学石油工程学院海工系　青岛　266580)



基于改进差分进化算法的潮流发电机组微观选址

王丛佼1，2王锡淮1陈国初2陈建民3陈晶1

(1.上海海事大学物流工程学院上海201306 2.上海电机学院电气学院上海200240 3.中国石油大学石油工程学院海工系青岛266580)

针对潮流能发电机组布局依赖经验法、缺乏自主优化而导致微观选址难度大的问题，提出了一种基于差分进化算法并结合流场仿真模型的微观选址优化方法。通过对流场的有限元仿真，获取选址区域在原始状态下的流速分布；在充分考虑地形、潮汐和尾流效应等因素的前提下，以仿真结果为依据，以潮流发电机组群输出功率最大为优化目标，以机组间距及水深限制为约束，建立微观选址优化的数学模型；采用差分进化算法进行模型求解，同时为更利于最优解的搜索，提出了对其变异算子及参数设置的改进策略。以龟山水道为例进行微观选址优化计算，验证了所提模型的准确性与算法的高效性。

潮流发电微观选址差分进化算法自适应潮流仿真

0　引言

近年来为应对常规化石能源面临枯竭及环境污染问题，开发可再生的清洁能源受到世界各国的高度重视。纵观各类清洁能源，潮流能能量密度大(远大于风能和太阳能)、可预测性高、不占用土地和不受气候影响等特点，实为可利用价值极高、潜力巨大的可开发能源[1]。我国海域辽阔，潮流能资源居世界前列，发展潮流能利用技术具有先天优势[2]。利用潮流能发电可解决海岛区域无电或缺电难题[3，4]，同时对推动智能电网建设、提高我国能源安全及改善能源结构具有深远意义。

规模化、产业化运行是潮流发电的现实趋势，随之带来的如何排布发电机组以提高能源利用率及发电经济性的微观选址问题[5]，成为国内外都亟待解决的关键环节之一。在实际流场中，发电机组的出力大小主要受具体地形条件、流速分布及上、下游机组间的尾流效应[6]等因素影响。其中尾流不仅会降低下游机组的出力，其产生的强大湍流还会影响发电机的使用寿命，因此微观选址不仅要求每个机组所在位置的潮流能密度尽可能高，而且需考虑如何保持相邻机组之间的距离从而使尾流的总体损耗最小。然而，目前工程中多采用的等间距“田”字形布放的经验法[7]不能充分考虑到上述因素，导致潮流能得不到合理、充分的利用，使发电效益受损。相比风力发电的研究[8-11]，针对潮流发电的微观选址问题的研究还在起步阶段。文献[12-14]基于水槽试验和数值模拟对机组的排布间距与形式进行了研究分析，但由于缺乏成熟、统一的计算软件与方法，所得结论存在一定差异，实用价值还尚未可知。文献[15]则借鉴风电场优化技术给出了适用于潮流发电机的尾流模型，建立了以产能为目标的机组布局优化模型，进而利用粒子群算法进行求解，并在算法中引入自适应罚系数来处理约束。该方法具有一定实用意义，但文中只基于规则矩形水道和理论流速公式进行计算，其流场模型过于理想，忽视了复杂地形海况对约束条件和流速分布的影响。针对上述局限，本文选取符合装机要求的实际水道进行高精度的流场仿真，以充分考虑地理的不规则性及流速分布的非均衡性，由此建立更符合实际情况的微观选址优化的数学模型。

由于模型精确性的提高，计算工作量也随之增大，从而需要高效的求解算法。差分进化算法(Differential Evolution，DE)作为一种新兴的优化计算技术，在电力系统相关领域已得到越来越多的应用[16-21]。独特的差分变异算子和贪婪选择机制使其具有强大的搜索能力，自提出以来在所有国际进化计算竞赛中都取得了极具竞争力的排名，这是其他任何一种单一的智能优化算法所不能比肩的[22]。然而经典DE算法存在种群多样性与收敛速度的矛盾及对参数敏感的不足，为此本文拟对其进行改进以进一步提高微观选址优化效果，实现水域潜能的最大发挥。同时，本文设计了符合流场特性的流体网格坐标系，给出了该坐标系下的变量表达形式及约束处理机制，进一步帮助算法提高求解效率。

1　潮流发电的流场建模

潮流发电机组的出力与其所在位置的潮流流速密切相关，获取流速分布是进行机组微观选址优化的必要前提。对流速的准确掌握可有效提高选址的合理性与经济性。本文在确定微观选址的区域范围之后，通过计算流体动力学(Computational Fluid Dynamics，CFD)技术[23]对该流场建模以得到所选区域的潮流流速分布，并进行实潮验证，控制误差在可允许范围内，从而为发电机组微观选址的最优化设计提供精确、可靠的潮流数据。

1.1流场区划

我国潮流能资源丰富，根据对130个主要水道的统计，理论平均功率可达13 948 MW[2]。其中舟山群岛的龟山水道储能巨大，其流向稳定，流速大(最大可达4 m/s)且能量密度高，水深、海床及通航条件均可满足装机的基本要求，因而具有可观的开发价值。本文选取该水道作为机组的选址区域。

1.2流速分布

本文基于CFD技术对上述流场区域进行潮流数值模拟。水动力模型采用正交性较好的四边形单元格，水动力推算引擎采用基于ADI的三维水动力差分模型。同时鉴于潮流仿真原理及模型的复杂性，本文从地理规模上分3个层次(东海大区域—舟山群岛—龟山水道)进行逐级的模拟计算，并根据国家海洋局的历史实测数据进行实潮验证，将通过验证的大区域中计算的模型参数，作为小区域的激励边界，以使所得流速分布结果更为准确。

龟山水道流场网格(规模为318×102)建模如图1a所示，水深分布如图1b所示。由于潮流根据潮汐运动而呈规律性变化，通常以一个朔望月(平均为29.53 d)为周期[1]进行计算。在一个周期内，为满足模型精确性，以10 min为一计算步长，即每隔10 min计算一次该流场模型内每一个网格节点的流速矢量，则最终输出为一个朔望月内每个计算步长下流场流速的矢量分布。如图2a、图2b所示，分别为某涨急和落急时刻(未放置机组时)的流速计算结果，可用于微观选址最优化计算的输入参数。

图1　龟山水道网格模型与水深分布Fig.1　The mesh model and water depth distribution of Guishan waterway

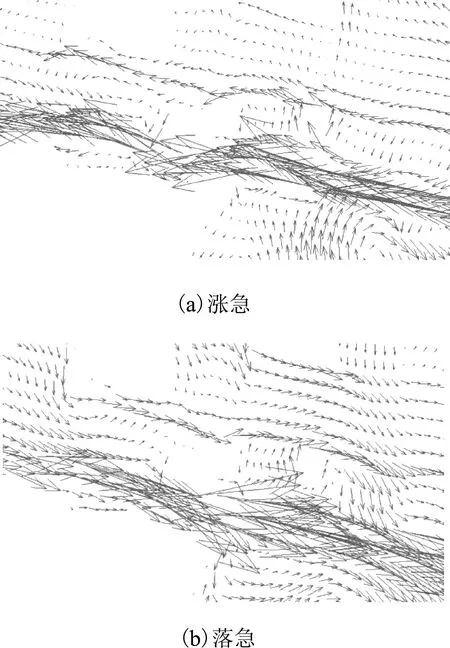
图2　龟山水道流速分布Fig.2　The velocity distribution of the maximum speed

2　微观选址优化的数学模型

2.1发电机组的功率模型

(1)

式中，t0、 t1分别为一个朔望月的起、止时间点；Pi(t，x，y，h)为机组i在三维坐标(x，y，h)位置、实际入流速度为Vi(t，x，y，h)时的发电功率。

对于Pi(t，x，y，h)与Vi(t，x，y，h)之间的关系，本文基于潮流发电机组的运行特性，参考风力机功率曲线，将其近似描述为一个分段线性函数

Pi(t，x，y，h)=

(2)

式中，A为水轮机桨叶的扫掠面积；ρ为海水密度，一般取1 025 kg/m3；Cp为功率系数；Vcutin、 Vcutout和Vrated分别为潮流发电机组的切入流速、切出流速和额定流速；P0为额定功率；Vi(t，x，y，h)为第i台机组的入流速度，该速度不仅与机组所处的地理位置(即初始状态下的潮流流速分布)有关，还受到与其他机组的相对位置引起的尾流效应影响[5]。

到目前为止，针对潮流能发电机组，还没有确切的尾流模型方程。文献[15]则将风力发电最常用的Jensen模型和Larsen模型应用于潮流发电中，并对两个尾流模型的测试数据与仿真所得数据之间的误差进行分析，进而发现Jensen模型的速度值偏差仅在0.01 m/s级别左右，能够较为实际地反映出潮流的尾流变化。应用于潮流发电的Jensen模型方程为

Vi，j(t，x，y，h)=

(3)

式中，Vi，j(t，x，y，h)为潮流经过机组j逐渐衰减而到达机组i时的速度(假设机组j在机组i上游)；Vj(t，x，y，h)为机组j的入流速度；CT为机组的推力系数；α为尾流衰减系数；X为两台机组在来流方向上投影的距离。

在实际流场中，任意潮流发电机均可能受到周围多台机组不同程度的尾流影响，假设动能损失与尾流损失守恒，则机组i的入流速度Vi(t，x，y，h)为

Vi(t，x，y，h)=VCFD(t，x，y，h)-

(4)

式中，VCFD(t，x，y，h)为由1.2节所获取的在未布置发电机组的情况下对应于坐标位置(x，y，h)的潮流速度；φj为影响因子，与两台机组的相对位置有关[13]。

2.2目标函数与约束条件

微观选址优化的目标是在保证机组可靠运行的前提下，确定各台发电机的具体位置，尽可能减小机组之间的潮流能损失，实现整体输出功率的最大化。鉴于DE算法用于求解全局最小化问题，则本文的目标函数为

(5)

即所有N台机组总平均功率的倒数。

该优化问题的基本约束条件为：

1)边界约束，即所有潮流发电机的位置都必须在所划定的水流场范围内。

2)水深约束，即

hi-ho>0

(6)

式中，hi为第i台机组桩脚所处深度；ho为海域水深下限，ho=R+hleg， hleg为机组桩脚至机轴的高度，R为水轮机叶片半径。

3)间距约束，即任意两台潮流发电机之间的距离都不能小于安全运行距离

(7)

式中，do为两机组间最小可行距离，即安全运行距离。一般情况下，设定do=3D，D为转子叶片直径。

3　基于改进差分进化算法的模型求解

由数学模型可知，潮流发电机组的微观选址优化是一个多变量、多约束的非线性优化问题，传统的数学方法往往无能为力。本文提出了一种基于动态有义集合的改进差分进化算法(dn-based Improved Differential Evolution，dn-IDE)应用于该问题的求解。同时，在求解过程中结合CFD设计了一种便于算法实现、节省计算量又兼顾流场特性的网格坐标系来表示机组位置变量，并给出了不同的约束处理方案。

3.1DE算法及其改进

基本DE算法的整体架构与遗传算法相似，通过变异、交叉、选择等操作产生新种群，经过迭代进化实现对全局最优解的搜索。其中变异操作是整个DE算法的核心，其基于不同个体间的差异对目标个体进行扰动来生成变异个体。目前，常用的变异算子有DE/rand/k和DE/best/k/两类，具体形式可见文献[22]。其中DE/rand/k由于基向量选择的随机性而有利于保持种群多样性，具有更好的求解稳定性，但易造成由于盲目带来的冗余计算量，一定程度减缓了算法的收敛速度；而类似DE/best/k算子，利用当前最优解指导群体搜索方向而使个体表现出极强的趋同性，加快向当前最优的靠拢，但易因种群多样性的大幅丢失而导致算法早熟，面对复杂高维多峰问题时，达不到所需要的求解精度。

可见，一个适宜的变异算子需要兼顾种群多样性与收敛速度，平衡算法的探测能力与开采能力。为此，本文设计了一种新的动态变异算子，其思想是：将种群中个体根据适应度函数值进行排序，对于求解最小化问题，适应度函数值越小的个体排名越前，则定义排名前dn(dn∈[1，2，…，NP])的个体组成有义集合(significant set)，从中随机选取一个有义解(significant solution)作为基向量来引导群体搜索方向，并且dn随迭代次数自适应调整，使有义集合具有动态规模。该变异算子的具体形式为

Vi，G=Xdn_sigset，G+F(Xr1，G-Xr2，G)

(8)

式中，G为当前进化代数；Xr1，G、 Xr2，G为从种群中随机选取的不同于目标个体Xi，G的差分个体；F为搜索步长；Xdn_sigset，G为从动态有义集合中随机选取的引导搜索的个体。dn的自适应策略为

(9)

式中，NP为种群规模；Gmax为最大进化代数；ceil(y)为大于y的最小整数。由上式可见，随着进化代数的增加，dn在[NP/2，1]区间内呈非线性递减，则在进化初期，可供选取的有义解范围相对较大，且dn的下降速率较慢，能够充分利用群体内的优秀信息共享，使个体得到更多有效搜索方向的引导，增大找到全局最优解的概率；而在进化后期，dn下降速率相对较快，有义解的选择更趋于当前最优解，从而引导个体趋于最优区域附近执行精细搜索，提高算法精度的同时加快收敛。

dn-IDE算法的交叉操作同基本DE算法，由目标个体Xi，G与变异个体Vi，G的每一维进行离散交叉而产生试验个体Ui，G=[u1，i，G，u2，i，G，…，uD，i，G]。

(10)

式中，rand(j)∈[0，1]为均匀分布的随机数；randn(i)∈[1，2，…，D]为随机选择的维数变量索引，以保证Ui，G至少有一位由Vi，G贡献，而对于其他位，由交叉概率因子CR决定，CR∈[0，1]。

由上可见，DE算法中有F和CR两个关键参数。关于两者的设置，有许多文献给出了推荐值，但没有统一的结论[24]，这主要是由于其与具体目标问题息息相关，不同的解空间分布甚至是对同一空间的不同搜索阶段都有不同的参数需求。而手动调节费时费力，降低算法的实用性。基于此，本文利用随机化参数来增加参数取值的多样性，同时使算法在无经验知识的情况下，自动产生适合当前搜索需要的值。经过多次试验，本文分别选取高斯分布和柯西分布来生成CR与F， 其中CR=N(0.5，0.01)， 则其以大概率落在0.5邻域内，在增加随机性的同时，一定程度上均衡目标个体和试验个体对下一代子个体的贡献。而F=C(0.5，0.05)能够充分地覆盖F的取值区间[0，1]，以在整个搜索过程中平衡算法的探索能力(较大取值)和开发能力(较小取值)。同时，相比高斯分布，柯西分布具有较高的两翼概率特性，能够产生分布性更广的随机数，从而使搜索步长更多样化以帮助算法摆脱局部极值点的干扰。

3.2编码方案

在微观选址优化问题中，优化变量为机组的位置坐标。实际工程中，通常使用笛卡尔坐标系(直角坐标)来表示空间位置，而应用于本文优化问题时该坐标存在一定的局限性：其横、纵轴与经纬度一致，但无法直接反映出所处位置的流速流向等数据，必须经过复杂的换算与判断机制才能求得目标函数所需信息，过程繁琐，计算量大。为此，本文结合流场特征，定义一种新的坐标系——流体网格坐标系。通过水动力场的仿真与调整，建立了这样一个网格：网格的一个维度m与流体流向一致，另一个维度n与流体的等势线一致。图3显示了第i台机组的网格坐标(mi，ni)与笛卡尔坐标(xi，yi)的对应关系。该网格坐标的优势在于：①由于坐标反映了流向信息，可以直接判断两点在流场中的相对位置，便于机组间上下游关系判断；②利用已包含流速信息和水深数据的网格节点作为选址点，方便可行，同时可大大降低计算规模，提高计算效率。

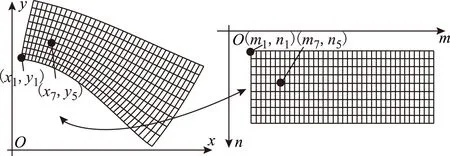
图3　笛卡尔坐标系与流体网格坐标系的对应示意Fig.3　The fluid grid coordinate system corresponding to Cartesian coordinate system

可见本文将有限单元格的节点处作为待选择的机组布放点，优化变量以整数形式出现。若给定N台机组，则解的编码形如(m1n1)，(m2n2)，…，(mNnN)]。解的长度(即维数)为2N，解的精度取决于网格精度，解的范围取决于网格行列数目。

3.3搜索范围

图4中曲线即通过CFD划定的选址边界，曲线内区域即为搜索范围。该区域上下为流线边界，左右为等势线边界，兼顾了流场特征、水路边界特征与四边形网格自身特征。其流线平均长度6 950 m，等势线平均长度1 575 m，由此建立的网格规模为：mmax=230，nmax=50，单元格尺寸为30 m×31 m，单边长度约为机组叶片直径的两倍，精度足够。

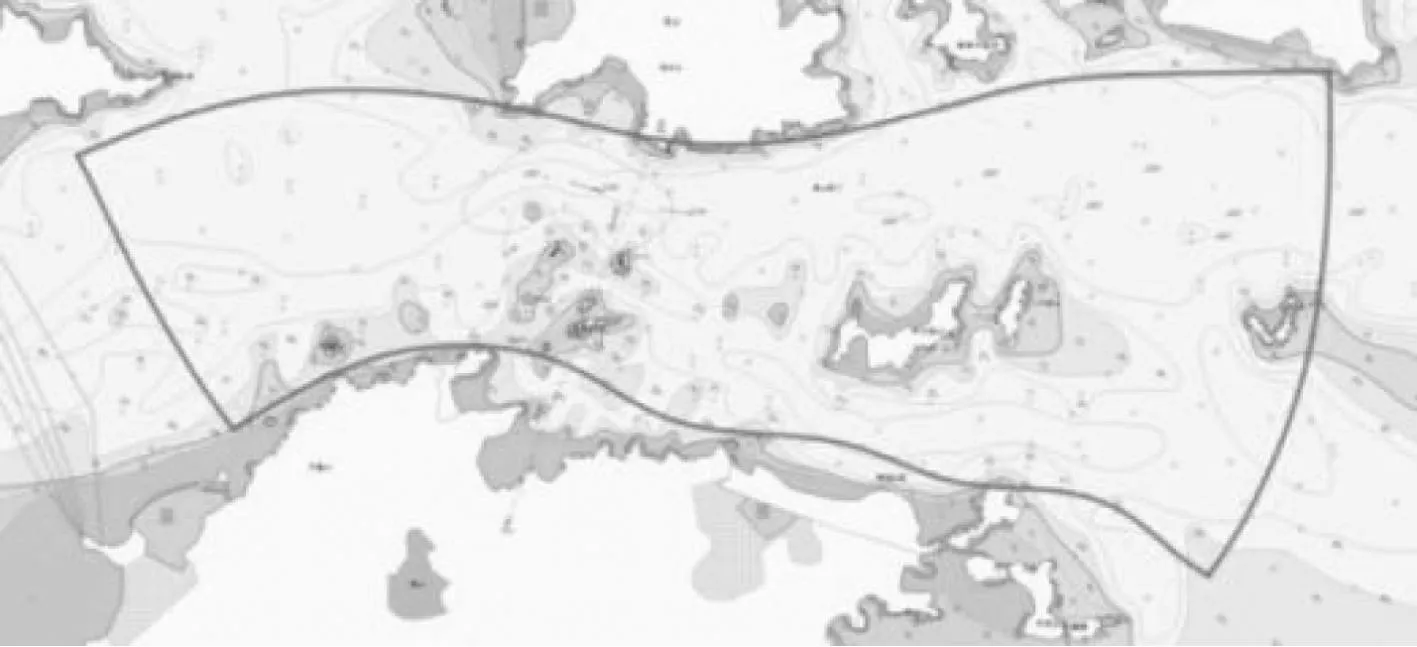
图4　待搜索范围Fig.4　The search range

3.4约束处理

约束条件的处理直接影响到算法的寻优效果。本文针对微观选址优化问题的不同约束，设计了各自处理不可行解的方案，以进一步提高算法效率。

1)超出边界范围

对于不符合边界条件的解，多数文献采用将其修复至边界的方法。该方法操作简单，但易使算法早熟于边界点，且在本文优化问题中，若机组在边界过于密集，易导致机组间距小于安全距离，不可行的几率依然极大。为此，本文设计了一种“镜面反射”修复机制，对超出边界的坐标变量关于邻近的边界做镜面映射，直至将其修复至边界内。同时该方法可提高算法对解空间搜索的遍历性，从而增大发现更优解的概率。

2)不满足水深条件

假设某解个体坐标落入浅水区域，则根据随机产生的方向将其迁移。对迁移路线所经过的节点进行水深判断，直至其跳出浅水区域。鉴于网格矩阵的规范化排布，随机方向可从8个邻近网格节点方向中选择。

3)违反安全间距

任意两台发电机组之间都需要满足安全间距，由此该约束条件的个数为N(N-1)/2， 且随着装机规模的增大，约束计算的复杂度也会显著增加。而本文设计了一种扫描排点法，在装机数量较大的情况下，可以有效减少计算量。扫描每个坐标周围不满足安全距离的所有节点位置，若发现解个体中存在第j台机组落在第i台机组的非安全区域内，则采用罚函数法对该不可行解进行惩罚。

(11)

式中，ΔF为惩罚项；C0为罚因子；机组i与机组j的间距为dij； ε为一小值正常数，确保分母不为零。

3.5求解步骤

1)通过CFD技术划定选址区域范围，获取该片区域的原始流速分布。

2)建立网格流体坐标系，记录网格中每一个节点包含的水深信息与实时流速流向信息；设定机组坐标上、下限(mmax，nmax)，(mmin，nmin)。

3)设置算法参数。包括最大迭代次数Gmax、 种群规模NP等，令进化代数G=0。

4)确定机组型号与数量，输入机组基本参数。

5)在坐标范围内随机均匀产生初始化种群，根据式(5)计算所有个体的适应度值并进行排序。

6)根据式(8)和式(10)对初始种群的个体进行变异、交叉操作，产生新的试验个体。

7)选择操作。比较试验个体与目标个体的适应度值，选取适应度值更优的个体进入下一代种群。

8)根据适应度值对个体排序，记录当前最优微观选址方案及其适应度值。

9)判断是否达到终止条件，若G=Gmax， 结束算法，输出结果；否则，G=G+1， 转至步骤6)。

4　微观选址优化算例分析

4.1实例描述

以龟山水道为例进行微观选址优化的仿真研究。该水道的水深分布如图1b，区划范围如图4所示。发电机组选取MCT公司的 “SeaGen”型潮流机[25]，其性能参数见表1。￣根据Flux法[1]及CFD技术对该水流场进行潮流能估算，可得装机数量为95台时较为合适。

表1　机组参数表Tab.1　Parameters of the turbine

4.2结果及比较分析

采用dn-IDE算法求解本文建立的微观选址优化模型，同时为验证模型及算法的有效性和优越性，分别运用经验“潮流田”法、标准DE算法及PSO算法[11]基于相同水道、相同机组对模型进行求解。其中，经验法一般将潮流发电机组按行列等间距交错放置[7]，沿与主潮流流向垂直的方向间距a倍直径距离，沿与主潮流流向平行的方向间距b倍直径距离，一般a和b依据实际情况与机组数量而定。本文针对龟山水道的经验选址方案如图5a所示。

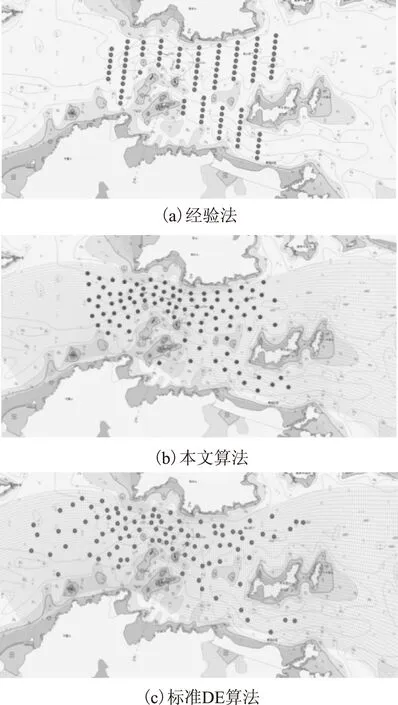
图5　各方法所得的最优微观选址方案效果图Fig.5　Renderings of the optimal solution for four methods

各算法的参数设置如下：标准DE采用最广泛应用的DE/rand/1变异策略，设置F=0.7，CR=0.9；PSO算法的参数见文献[11]；所有算法统一设定种群规模为50，最大迭代次数为5 000。表2给出了3种算法运行50次的仿真统计结果及经验法所得结果。

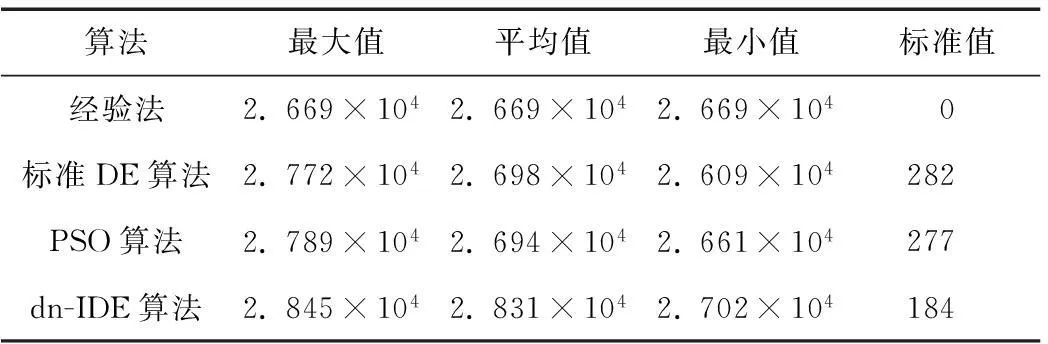
表2　不同布局方案总发电功率统计表Tab.2　The generation power for different layout schemes　(单位：kW)

从表2可见，经验法所得结果最不理想，该方法虽简单易行，但相比3种优化算法，由于未能充分考虑流场分布及尾流效应等对微观选址至关重要的因素，使得潮流能损失较大，潮流发电机组的出力还有一定待提高空间。而本文算法求得目标函数的最优值为3.514 9×10-5，对应一个朔望月周期内的总平均功率为2.848×104kW(每台机组的具体坐标见附表1)，比经验法所得提高了6.59%，明显提高了电能产值，增强了潮流能利用的合理性。同时与标准DE算法、PSO算法所获取的结果相比，本文算法最优方案的发电功率分别提高了2.63%和2.01%，验证了该算法对求解质量的改善能力，并且在平均值、最小值和标准差方面都表现最好，进一步显示了dn-IDE算法求解高维复杂优化问题的稳定性。

图5b～图5d分别给出了dn-IDE算法、标准DE算法及PSO算法所得的最优方案效果图。通过比较，

可以看出图5c和图5d中机组分布较不均衡，各潮流发电机组相互之间的尾流影响差异大，显然对潮流能的利用不够充分。而本文算法的最优方案图5b中潮流发电机组分布较为合理，错落有致，在降低机组相互之间尾流效应影响的同时，保证了有效潮流能的充分发挥，从而使机组符合实际的自主最优布局而实现产能最大化，提高了微观选址的经济性与合理性。

图6给出了3种优化算法的收敛曲线。从图中可以看出，dn-IDE算法收敛速度相对其他两种算法拥有明显的优势，可以在较少的迭代次数内获得更好的寻优质量，显示了该算法寻优的有效性与先进性。

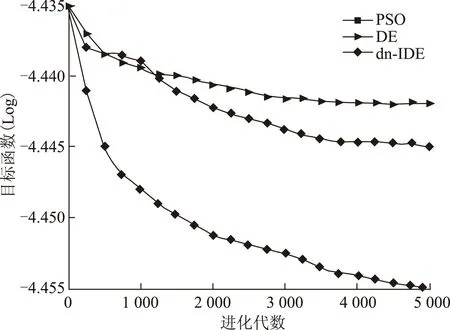
图6　收敛曲线Fig.6　The convergence curves

5　结论

本文为潮流发电机组的微观选址提供了一种基于差分进化算法的优化设计方法。在充分考虑实际地形条件、尾流效应及安全距离等因素的前提下，建立了微观选址优化的数学模型，并通过潮流场的有限元仿真计算流速分布，提高模型的准确性与实用性；设计了符合流场特征、便于算法寻优的网格流体坐标系，进而提出了将改进差分进化算法与其结合进行模型求解的新方法。为检验模型及算法的应用性能，对实际海域进行了仿真实验。结果证明，该选址方法能使潮流发电机组符合实际的自主最优布局而实现产能最大化，克服了经验选址的局限性，为潮流能合理、高效地开发提供了新的思路，具有一定的工程应用价值。

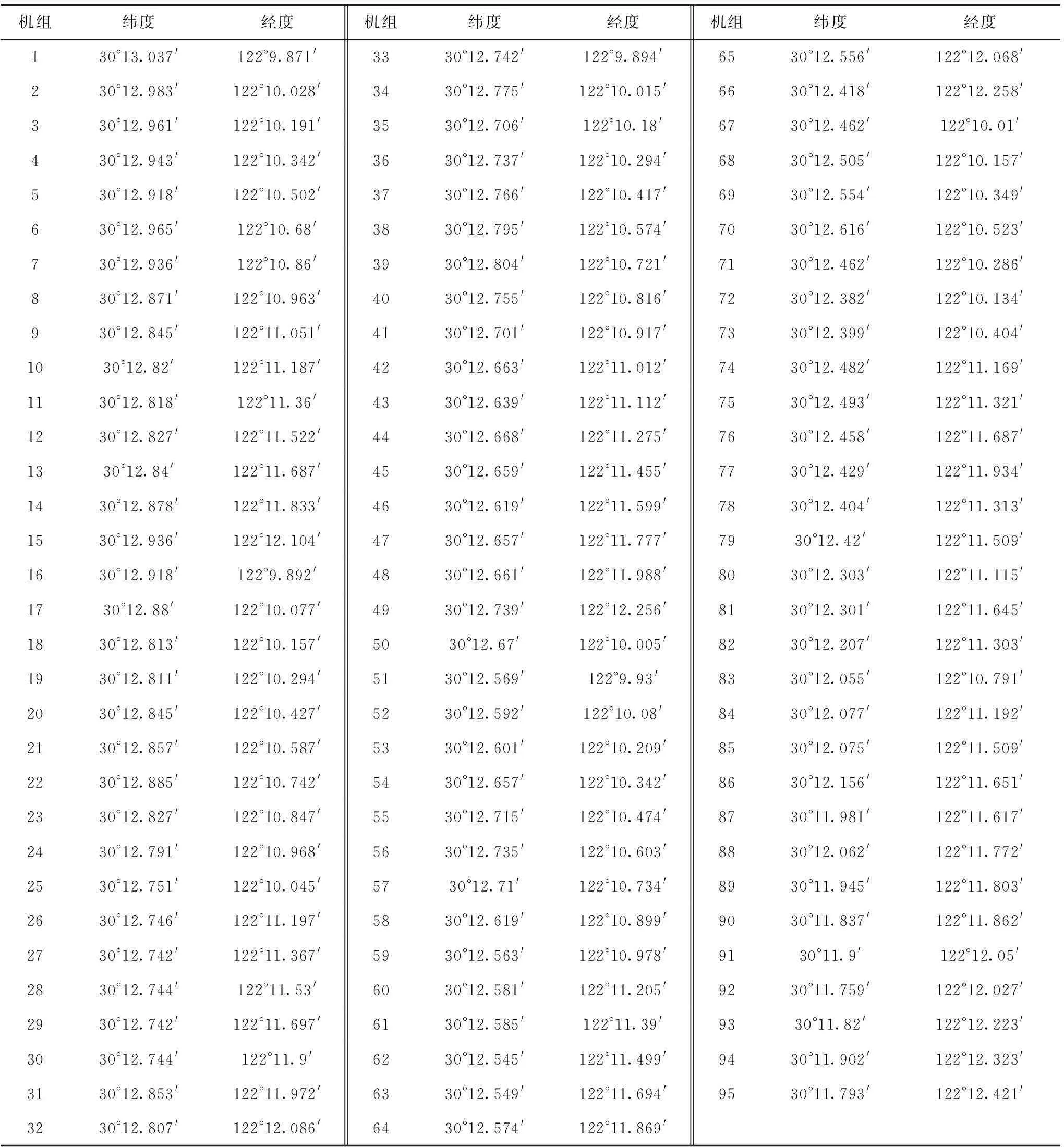
附表1　本文所得最优方案中机组各具体坐标App.Tab.1　The specific coordinates of the unit in the optimal scheme

[1]Bahaj A S.Generating electricity from the oceans[J].Renewable and Sustainable Energy Reviews，2011，15(7)：3399-3416.

[2]Wang Shujie，Yuan Peng，Li Dong，et al.An overview of ocean renewable energy in China[J].Renewable and Sustainable Energy Reviews，2011，15(1)：91-111.

[3]杨欢，赵荣祥，辛焕海，等.海岛电网发展现状与研究动态[J].电工技术学报，2013，28(11)：95-105.

Yang Huan，Zhao Rongxiang，Xin Huanhai，et al.Development and research status of island power systems[J].Transactions of China Electrotechnical Society，2013，28(11)：95-105.

[4]杨俊友，王海鑫，邢作霞，等.孤岛模式下潮流能发电系统协调控制策略[J].电工技术学报，2015，30(14)：551-560.

Yang Junyou，Wang Haixin，Xing Zuoxia，et al.Coordination control strategy of tidal power generation in island grid[J].Transactions of China Electrotechnical Society，2015，30(14)：551-560.

[5]Blunden L S，Bahaj A S.Tidal energy resource assessment for tidal stream generators[J].Proceedings of the Institution of Mechanical Engineers：Part A Journal of Power Energy，2007，221(A2)：137-146.

[6]MacLeod A J，Barnes S，Rados K G.Wake effects in tidal current turbine farms[C]//Proceedings of the MAREC Conference，Newcastle，2002：49-53.

[7]Fraenkel P L，Paish O，Gava P.The exploitation of tidal and marine currents：wave energy：project results[M].Brussels Luxembourg：European Commission，1996.

[8]许昌，杨建川，李辰奇，等.复杂地形风电场微观选址优化[J].中国电机工程学报，2013，33(31)：58-64.

Xu Chang，Yang Jianchuan，Li Chenqi，et al.Optimization of wind farm layout in complex terrain[J].Proceedings of the CSEE，2013，33(31)：58-64.

[9]黄晟，王辉，廖武，等.基于VSC-HVDC海上串联拓扑风电场低电压穿越控制策略研究[J].电工技术学报，2015，30(14)：362-369.

Huang Sheng，Wang Hui，Liao Wu，et al.Control strategy based on VSC-HVDC series topology offshore wind farm for low voltage ride through[J].Transactions of China Electrotechnical Society，2015，30(14)：362-369.

[10]汪璐，邵如平，王雅璐.基于海上大型风电场VSC-HVDC系统电网侧控制器的设计[J].电力系统保护与控制，2015，43(17)：107-112.Wang Lu，Shao Ruping，Wang Yalu.Grid side controller design of VSC-HVDC system based on large offshore wind farm[J].Power System Protection and Control，2015，43(17)：107-112.

[11]万春秋，王峻，杨耕，等.基于静态评价粒子群的风电场微观选址方法[J].太阳能学报，2012，33(12)：2185-2191.

Wan Chunqiu，Wang Jun，Yang Geng，et al.Wind farm micro-siting based on particle swarm optimization with static evaluation[J].Acta Energiae Solaris Sinica，2012，33(12)：2185-2191.

[12]Seung H L，Sang H L，Kyungsoo J.A numerical study for the optimal arrangement of ocean current turbine generators in the ocean current power parks[J].Current Applied Physics，2010，10(S2)：137-141.

[13]Myers L E，Bahaj A S.Simulated electrical power potential harnessed by marine current turbine arrays in the alderney race[J].Renewable Energy，2005，30(11)：1713-1731.

[14]O’Doherty D M，Mason J A，Morris C，et al.Interaction of marine turbines in close proximity[C]//Proceedings of 9th European Wave and Tidal Energy Conference，Southampton，2011.

[15]刘丞，汪昆，汪雄海.基于粒子群算法的潮流发电机布局[J].浙江大学学报(工学版)，2013，47(12)：2088-2093.

Liu Cheng，Wang Kun，Wang Xionghai.Optimal deployment of tidal current turbines based on particle swarm algorithm[J].Journal of Zhejiang University (Engineering Science)，2013，47(12)：2088-2093.

[16]邱威，张建华，刘念.考虑环境因素和电压稳定性的多目标最优潮流[J].电工技术学报，2012，27(2)：190-197.

Qiu Wei，Zhang Jianhua，Liu Nian.Multi-objective optimal power flow considering environmental factor and voltage stability[J].Transactions of China Electrotechnical Society，2012，27(2)：190-197.

[17]康忠健，訾淑伟.基于差分进化算法的油田区域配电网无功优化技术的研究[J].电工技术学报，2013，28(6)：226-231.

Kang Zhongjian，Zi Shuwei.Research on the reactive power optimization of oil-field regional distribution network based on differential evolution[J].Transactions of China Electrotechnical Society，2013，28(6)：226-231.

[18]张建华，于雷，刘念，等.含风/光/柴/蓄及海水淡化负荷的微电网容量优化配置[J].电工技术学报，2014，29(2)：102-112.

Zhang Jianhua，Yu Lei，Liu Nian，et al.Capacity configuration optimization for island microgrid with wind/photovoltaic/diesel/storage and seawater desalination load[J].Transactions of China Electrotechnical Society，2014，29(2)：102-112.

[19]王荣杰，詹宜巨，周海峰，等.基于差分进化机理优化的PID控制的AVR系统[J].电力系统保护与控制，2015，43(24)：108-114.

Wang Rongjie，Zhan Yiju，Zhou Haifeng.PID controlled AVR system based on differential evolution mechanism optimization[J].Power System Protection and Control，2015，43(24)：108-114.

[20]吕忠，周强，蔡雨昌.含分布式电源的DEIWO算法配电网无功优化[J].电力系统保护与控制，2015，43(4)：69-73.

Lü Zhong，Zhou Qiang，Cai Yuchang.Reactive power optimization in distribution network with distributed generation on DEIWO algorithm[J].Power System Protection and Control，2015，43(4)：69-73.

[21]邹必昌，孙洪斌，龚庆武，等.含分布式发电的改进混合整数差分算法的配电网重构[J].电力系统保护与控制，2012，40(12)：25-30.

Zou Bichang，Sun Hongbin，Gong Qingwu，et al.Reconfiguration of distribution system using improved mixed-integer differential evolution with distributed generations[J].Power System Protection and Control，2012，40(12)：25-30.

[22]Price K，Storn R.Differential evolution-a practical approach to global optimization[M].Berlin：Springer Verlag，2006：133-152.

[23]李莉，刘永前，杨勇平，等.基于CFD流场预计算的短期风速预测方法[J].中国电机工程学报，2013，33(7)：27-32.

Li Li，Liu Yongqian，Yang Yongping，et al.Short-term wind speed forecasting based on CFD pre-calculated flow fields[J].Proceedings of the CSEE，2013，33(7)：27-32.

[24]Das S，Suganthan P N.Differential evolution：a survey of the state-of-the-art[J].IEEE Transactions on Evolutionary Computation，2011，15(1)：4-31.

[25]Fraenkel P L.Marine current turbines：pioneering the development of marine kinetic energy converters[J].Proceedings of the Institution of Mechanical Engineers，Part A：Journal of Power and Energy，2007，22l(A2)：159-169.

Tidal Current Turbines Micrositing Based on Improved Differential Evolution Algorithm

Wang Congjiao1，2Wang Xihuai1Chen Guochu2Chen Jianmin3Chen Jing1

(1.Logistics Engineering CollegeShanghai Maritime UniversityShanghai201306China 2.Department of Electrical EngineeringShanghai Dianji UniversityShanghai200240China 3.School of Petroleum EngineeringChina University of PetroleumQingdao266580China)

A micrositing method based on differential evolution algorithm combined with flow field simulation model is proposedfor solving the problems that tidal generator layout depends on experience without optimization technology.This method firstly employsthe finite element simulation to obtain the original flow velocity distribution.Then a mathematical model based on the simulation results is built in full consideration of topography，tide，and wake effect.The objective function is the maximization of the whole tidal turbines’ power outputand the free variables are the turbines’ coordinates which are subject to the minimum distance conditions and the depth conditions.In order to solve this model，an improved differential evolution algorithmis proposed，in whichthe adaptive mutation operator and parameters increase the global search ability.The micrositing of tidal turbines is performed on the Guishan waterway.Then the optimized results demonstrate the accurateness of the proposed model and the effectiveness of the solving algorithm.

Tidal power，micrositing，differential evolution algorithm，adaptive，tide simulation

2015-04-28改稿日期2015-09-02

TM612

王丛佼女，1984年生，博士，讲师，研究方向为电力系统优化设计及智能控制。

E-mail：qinxiaojiayi@hotmail.com(通信作者)

王锡淮男，1968年生，教授，研究方向为复杂系统优化及控制。

E-mail：wxh@shmtu.edu.cn

国家自然科学基金(61573240)、国家体育总局科研项目(2015HT056)和上海市教委科研创新重点项目(12ZZ158)资助。