基于动力测试的混凝土连续梁桥有限元模型修正

赵崇基，张　巍，刘志华，韩之江

(1.太原理工大学建筑与土木工程学院， 山西太原030024；2.山西省交通科学研究院， 山西太原030024)



基于动力测试的混凝土连续梁桥有限元模型修正

赵崇基1，张巍1，刘志华2，韩之江2

(1.太原理工大学建筑与土木工程学院， 山西太原030024；2.山西省交通科学研究院， 山西太原030024)

为探讨有限元模型修正方法在桥梁结构运营安全性能评估中的有效性，提出了基于动力测试的混凝土连续梁桥有限元模型修正方法。利用有限元软件ANSYS建构了装配式预应力混凝土连续箱梁桥的有限元模型，以动力试验获得竖向前6阶自振频率作为状态变量，构造目标函数。通过分析目标函数对设计参数的灵敏度，选取灵敏度高的设计参数对模型进行修正，调整了模型的物理参数，使模型计算值与试验结果在合理的误差范围内。而后对修正后的模型按照现场实桥荷载试验加载工况进行加载，用现场实桥荷载试验的结果验证了模型修正方法的正确性，表明了修正后的模型能够较准确地反映桥梁结构的实际运营状况，可作为桥梁运营安全性能评估以及维修加固的基准分析模型，具有实际的工程应用价值。

混凝土连续梁桥；有限元；模型修正; 动力测试

0　前　言

目前，桥梁结构运营安全性能的评估和承载能力的鉴定广泛采用实桥荷载试验的评定方法[1]。但实桥荷载试验准备周期较长、试验加载设备和加载程序复杂、观测仪器布置受高空和气候条件制约影响较大、试验费用昂贵，总体效益低下。因此，探索基于动载实测数据的结构有限元模型修正方法应用于桥梁结构运营安全性能评估，不失为一种高效便捷的技术方法。当前结构模型修正方法已成为桥梁工程界的研究热点。Frant等[2]采用基于灵敏度分析的方法进行了结构模型的修正。Snanyei等[3]利用静载试验测试的结果，对某小型钢结构模型进行了有限元修正。杜青等[4]以环境振动试验的测试数据为目标值，运用基于优化理论的动力模型修正方法对河北邢台地区的青洞大桥进行了有限元模型修正。邓苗毅等[5]利用某在役五跨连续箱梁桥静力试验的测试结果，对其结构有限元模型参数进行了修正。方志等[6]基于多状态下静动力试验获得静力位移和模态测试结果，运用参数灵敏度分析和ANSYS优化技术对主跨180 m的独塔双索面预应力混凝土斜拉桥的一个1∶15的缩尺模型进行了有限元修正。殷广庆[7]应用基于正交试验的响应面模型和遗传算法对辽阳市中华大桥进行了有限元模型修正，并利用修正后的有限元模型对该桥的极限承载力与疲劳性能进行了分析。何涛等[8]联合动静载试验数据，综合运用动态加权系数和灵敏度分析方法对两榀预应力混凝土梁进行了模型修正。谢瑞杰[9]以湖南衡阳某预应力钢筋混凝土下承式系杆拱桥为研究背景，运用基于静动力有限元模型修正的方法对该桥进行了承载力的评估，验证了其安全性能。这些研究在桥梁结构状态评估和剩余寿命预测上具有一定参考价值。目前提出的应用动力试验测得的多阶频率和振型数据进行模型修正的方法，由于动力响应试验存在着试验模态不完备，高阶振型无法准确测量，测试结果受噪声干扰误差较大等缺点导致该方法在工程实践中局限性较大。本文提出的模型修正方法，采用灵敏度分析方法，以易于准确测得竖向前6阶自振频率实测数据对基于设计资料的有限元模型进行修正。而后对修正后的有限元模型按照实桥荷载试验加载工况进行加载，模拟分析了实桥荷载试验加载工况下预应力混凝土连续梁桥有限元模型的挠度计算结果，与现场实桥荷载试验测试结果相比较，两者更加吻合。表明本文提出的方法可以应用于对预应力混凝土连续梁桥的运营安全性能评估中。

1　现场动载试验

本实桥荷载试验在山西境内得胜口至大同的某高速公路上跨越大同开发区的一座全长2 294.68 m的高架桥上进行。该桥上部结构为15联77跨预应力混凝土现浇和装配式连续箱梁，下部结构为柱式墩、板式墩、肋式台，基础为钻孔灌注桩。设计荷载为：汽车—超20级、挂车-120。本试验选取其中1联7跨的预应力混凝土装配式连续箱梁桥(第68至74跨)作为试验对象。限于篇幅，本文仅对动载测试做一简述。

采用环境随机激励法，采集桥梁结构在无荷载状况下的自由振动响应信号。选用DH610超低频高灵敏度拾振器采集结构的响应信号，测试仪器选用DH5907A无线环境激励桥梁模态测试分析系统，测量信号存入电脑硬盘。经模态分析处理，获得结构的自振特性参数，包括自振频率、模态振型和阻尼比。具体工作流程如图1所示，振动试验测点布置如图2。

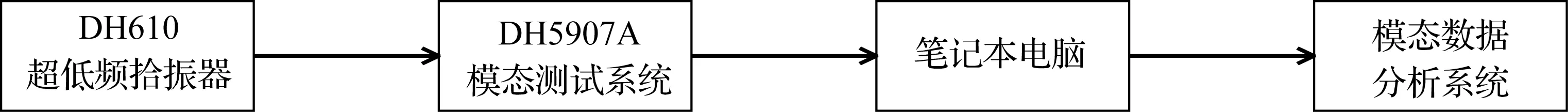
图1自振特性测试工作流程图

Fig.1Figure of the natural vibration characteristic testing process

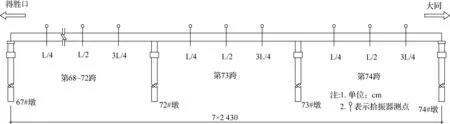
图2　振动测试点布置图

2　混凝土连续梁桥有限元模型的建立

2.1初始有限元模型

采用有限元通用软件ANSYS,按照该桥的设计资料，对试验段1联7跨的预应力混凝土装配式连续箱梁桥构建其上部结构的初始有限元模型。箱梁采用shell63单元模拟，箱梁顶板与桥面铺装层作为一个整体建立模型，由于箱梁与桥面铺装层用的混凝土型号不同(箱梁采用C50混凝土，桥面板铺装层采用C40混凝土)，桥面板铺装层厚度按式(1)进行等效计算，防撞墙和防撞护栏以质量单元mass21加于节点上，共划分38 570个单元。预加力采用等效荷载法施加于梁体模型的作用区段，并计入预应力损失的影响。

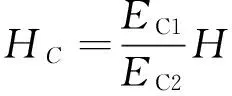
(1)

式中：H为桥面铺装层厚度，HC为等效的桥面铺装层，EC1为C40混凝土的弹性模量，EC2为C50混凝土的弹性模量。设计参数初始值见表1,有限元模型如图3和图4所示。

表1　设计参数初始值Tab.1　The initial value of design parameters

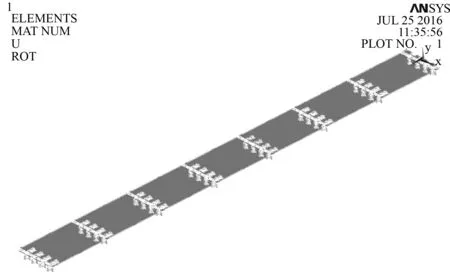
图3有限元模型立面图

Fig.3The elevation of the finite element model

图4有限元模型局部图

Fig.4The local figure of the finite element model

2.2初始有限元模型计算结果

为了提高模型修正的准确性，利用振型相关系数MAC来定量的检验计算模态和实测模态的相关性，MAC值越接近于1，则表明计算模态和实测模态的相关性越好。模态分析的数值结果见表1。

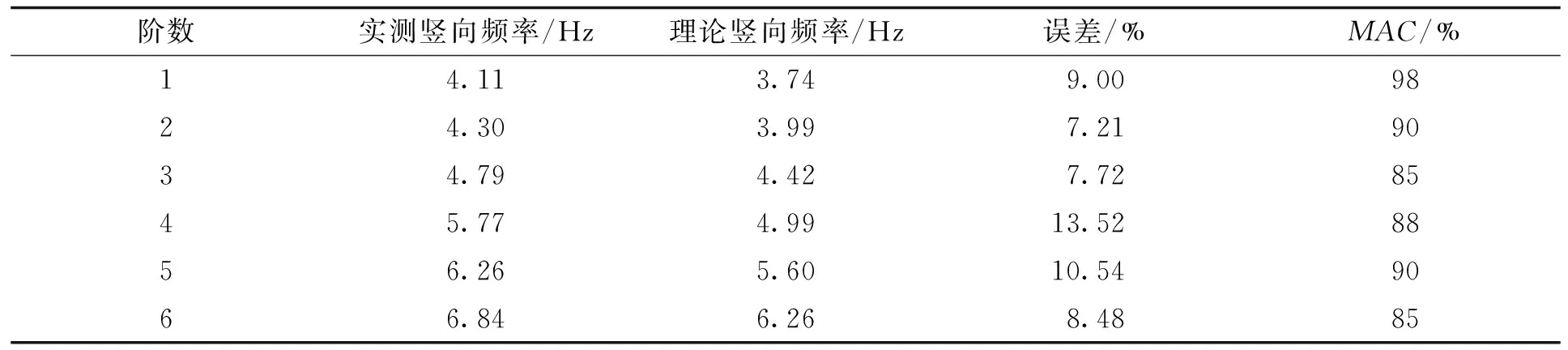
表2　模型计算与试验结果对比Tab.2　Comparisons between the model calculation and the results of the test

由表2可知，桥梁结构有限元理论计算的固有频率比试验测试结果偏小，说明在构建有限元初始模型时，结构的刚度取值相比实际值偏小；由MAC值的大小可知，计算模态和实测模态的相关性有待提高。因此有必要对模型进行修正。

3　目标函数的构造以及参数灵敏度分析

3.1目标函数

本文根据试验和理论的频率值构造目标函数[10]:

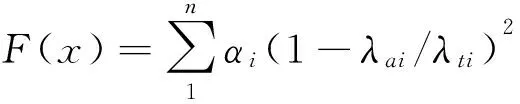
(2)

其中：F为基于动力测试频率的目标函数；λai为频率理论计算值，这里为结构前6阶竖向频率有限元计算值；λti为频率实测值，这里为结构前6阶自振频率实测值；αi为各阶自振频率权重系数，取1/6。

3.2设计参数灵敏度分析

修正参数的选取，直接关系到有限元模型修正的成败和优化效率。应遵循两个基本原则[10]，一是选取的参数不能过多，因为桥梁结构实测的数据有限，参数太多不但分析和优化的工作量太大，还会使优化迭代陷入局部最优解；二是选择灵敏度相对高的参数，但是要结合工程经验。因为结构优化的目标函数基本上是由灵敏度较高的参数控制的，若选择灵敏度低的参数，会增大有限元模型的误差。但是灵敏度较高的参数并不一定是实际发生变化的参数，这样就导致修正结果的不合理。因此在修正参数的选取上，应该依据灵敏度分析[11]并结合实际工程经验合理地选取。

依据工程设计经验,考虑到桥面铺装层以及混凝土的材料参数受施工因素的影响，与设计值存在偏差，故选取桥面铺装层厚度H、混凝土弹性模量E、密度Dens、泊松比μ等参数作为设计参数，并进行灵敏度分析[6,12-13]。

目标函数对设计变量的灵敏度为：

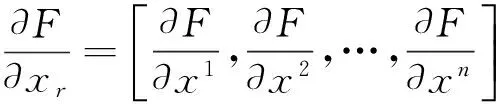
(3)

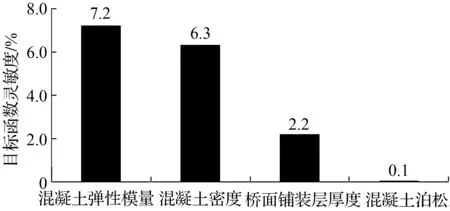
图5　目标函数对设计参数灵敏度Fig.5　Sensitivity of objective function to the design variables

用ANSYS中的最优梯度法对设计参数进行灵敏度分析，得到桥梁结构有限元模型中设计参数变化(±1)%，目标函数对于设计参数的绝对灵敏度，见图5。

通过灵敏度分析可见：频率计算结果对混凝土的泊松比不敏感，混凝土的弹性模量和密度则对频率的计算结果影响很大，而桥面铺装层厚度H次之。故将混凝土的弹性模量E、密度Dens、桥面铺装层厚度H，选取为待修正的设计参数。

这里需要说明的，相关文献研究表明[8，14]，在预应力混凝土梁未出现开裂的状态下，预应力束的布置方式和线型对混凝土梁的自振频率有影响，而不同预应力大小对混凝土梁的自振频率没有影响。故本文未对预应力数值进行修正。

4　模型修正计算结果

利用有限元软件ANSYS优化时[6]，先采用零阶法中的子空间法(Sub-Problem法)获得全局最小值，接着用一阶方法对结果进一步优化计算，最终得到使目标函数取得最优值的最佳序列计算结果，见表3：

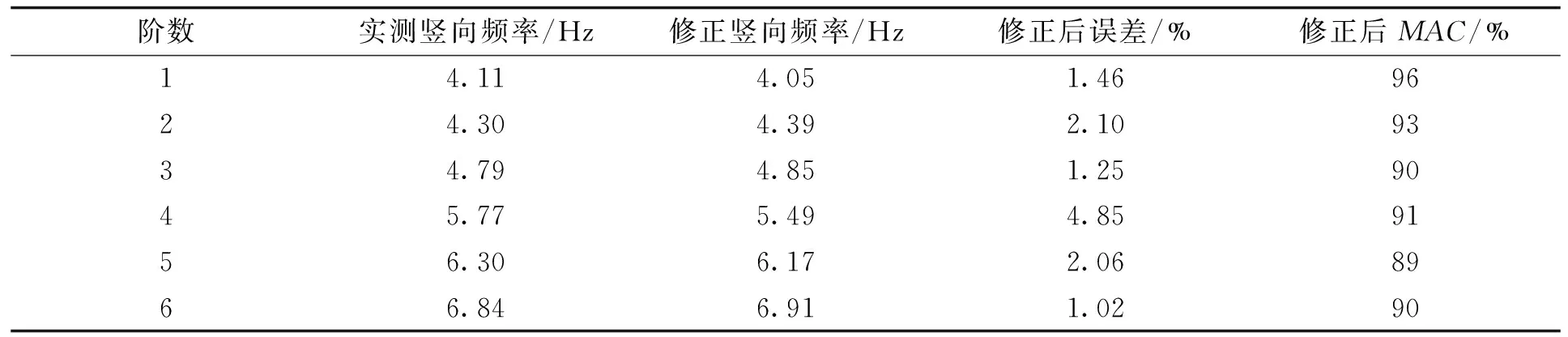
表3　修正前后数据对比Tab.3　Data comparisons between the test and modified

多次优化迭代后设计参数修正值，见表4。

表4　设计参数初始值与修正值Tab.4　The values of design parameters before and after the modification

从表4可看出，混凝土连续梁桥的弹性模量比设计值增大约39.71%，这一方面是由于混凝土弹性模量随龄期增长而增长所致。另一方面，也考虑到支模偏差、梁内钢筋的影响，使得梁截面的惯性矩与设计值不符，故本文修正的混凝土弹性模量表征的是对整个桥梁结构刚度的修正。

修正后的桥面板厚度比设计值增大了0.015 m,是由于施工时桥面铺装层厚度和不平整度控制不均等因素造成的。混凝土的密度理论值为2 550 kg/m3,考虑到混凝土中的配筋率和施工时混凝土的均匀程度，其密度与修正后的值接近。

5　有限元模型数值计算结果与现场实桥荷载试验结果的比较

将修正后模型按照实桥荷载试验加载工况进行加载，模拟分析实桥荷载试验加载下73跨的1#梁1/4、1/2、3/4截面处的挠度以及2#、3#、4#梁的1/2截面处的挠度，并与现场实桥荷载试验测试结果进行比较。测试断面位置如图6所示，汽车荷载和挠度测点布置见图7。

(a) 车辆加载平面布置图

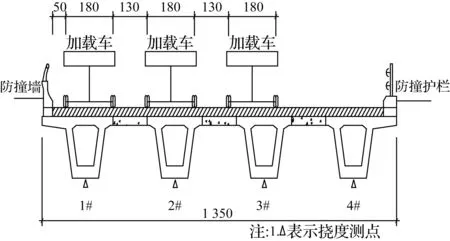
(b) 车辆横桥向排列与主梁挠度测点布置图

图7车辆布置与挠度测点横向布置示意图

Fig.7Vehicle arrangement and the deflection point horizontal layout diagram

实桥荷载试验加载下各测点的竖向挠度的结果对比见表5。

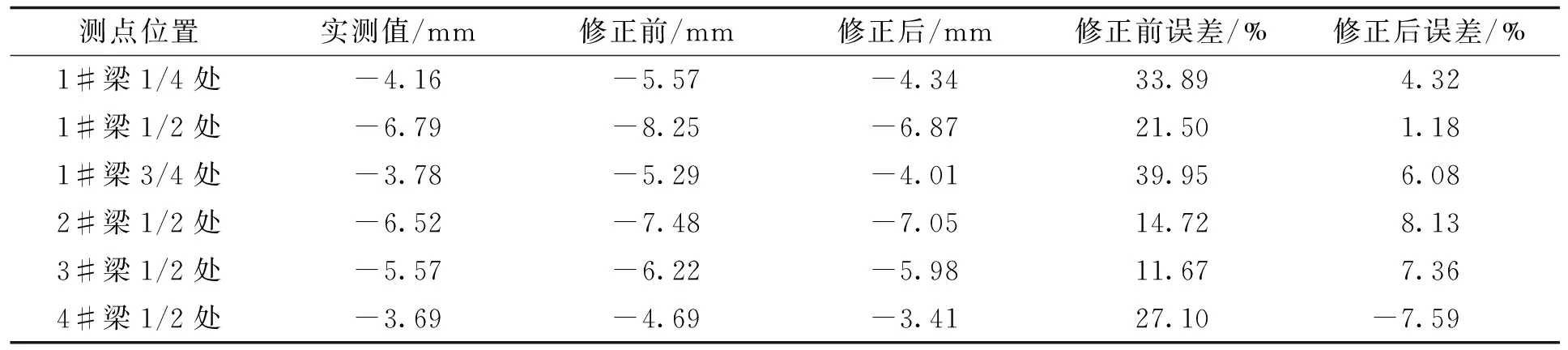
表5　实桥竖向挠度实测值与修正后模型计算值对比Tab.5　The comparisons of each measuring point’s deflection between the tested and modified under static load test load

由表5可以看出，修正后的模型在实桥荷载试验加载下各测点的竖向挠度值与实测值相当接近，相对误差在10%以内。说明修正后的模型达到了较高的计算精度，能够较准确地反映桥梁的真实运营状况。

6　结　语

①本文应用基于灵敏度分析的设计参数型修正方法，在有限元软件ANSYS优化设计平台上，采用壳单元shell63建构有限元模型，依据动力测试获得的前6阶竖向自振频率对预应力混凝土连续梁桥进行模型修正，通过了现场实桥荷载试验结果的验证。

②本文提出的模型修正方法，通过与现场易于准确测量的动测前6阶竖向频率相结合，就能够有效地应用于预应力混凝土连续梁桥的结构状态评估。这对探索和完善桥梁结构运营安全性能评估的工程应用具有参考价值。

③模型修正的数值计算结果表明，对于预应力混凝土连续梁桥的结构状态评估，选取混凝土主梁弹性模量、混凝土密度和桥面铺装层厚度作为设计参数，能够获得满足工程精度的修正模型，可为类似实际工程应用提供借鉴。

[1]交通运输部公路科学研究院.JTG/T J 21—2011 公路桥梁承载能力检测评定规程[S]. 北京: 人民交通出版社，2011.

[2]FARHAT C,HEMEZ F M.Updating finite element dynamic models using an element-by-element sensi-tivity methodology[J]. AIAA Journal,1993,31 (9):1702-1711.

[3]SANAYEI M, IMBARO G R.Structural model updating using experimental static measurements[J]. Journal of Structural Engineering, ASCE, 1997, 123(6): 792-798.

[4]杜青,蔡美峰,张献民,等.钢筋混凝土桥梁结构动力有限元模型修正[J]. 公路交通科技,2006,23(1): 60-62 .

[5]邓苗毅,任伟新.基于静力荷载试验的连续箱梁桥结构有限元模型修正[J]. 福州大学学报(自然科学版),2009,37(2): 261-266.

[6]方志,唐盛华,张国刚,等.基于多状态下静动态测试数据的斜拉桥模型修正[J]. 中国公路学报,2011(1):34-41.

[7]殷广庆.梁式桥有限元模型建立与修正及其应用[D]. 大连:大连理工大学，2013.

[8]何涛,张巍,吴植安.基于动静载试验数据预应力混凝土梁模型修正方法试验研究[J]. 公路交通科技，2015,12(3):75-80.

[9]谢瑞杰.基于静动力有限元模型修正的既有钢筋混凝土拱桥承载力评估[D]. 长沙：中南大学,2010.

[10]宗周红,任伟新.桥梁有限元模型修正和模型确认[M]. 北京:人民交通出版社,2012.

[11]魏锦辉,任伟新.基于响应面法的桥梁静动力有限元模型修正[J]. 公路交通科技,2015,2(32)：68-73.

[12]王英,孙利民.大跨连续刚构桥材料参数模态敏感性分析[J]. 广西大学学报:自然科学版,2015,40(1)：142-148.

[13]万利军,单炜,姜华.基于响应面法的桥梁动力学有限元模型修正[J]. 公路交通科技,2014,8(31)：96-101.

[14]DALL’ASTA A, DEZI L.Discussion about prestress force effect on vibration frequency of concrete bridges[J]. Journal of Structural Engineering,ASCE,1996,122(4):458.

(责任编辑唐汉民梁碧芬)

Finite element model updating on continuous concrete girder bridge based on dynamic test

ZHAO Chong-ji1, ZHANG Wei1, LIU Zhi-hua2, HAN Zhi-jiang2

(1.College of Architecture and Civil Engineering,Taiyuan University of Technology,Taiyuan 030024,China;2.Shanxi Traffic Science Research Institute, Taiyuan 030024,China)

In order to explore the effectiveness of finite element model updating method in safety performance assessment of bridge structures, a finite element (FE) model updating method for continuous concrete girder bridge structure based on dynamic test is proposed. The finite element model of a prefabricated prestressed continuous concrete girder bridge was set up with ANSYS. An objective function was constructed by taking the first six orders of vertical vibration natural frequency as the state variables. After the sensitivity analysis was conducted on the design variables, high sensitivity design variables were selected to modify the model. The results showed that, after the model being modified, the errors between the calculated values of the model and the test results converged into a reasonable error range. Afterwards, the updated model is loaded according to the loading of actual bridge, and the test results of the bridge demonstrate the validity of the model updating method, which proves that the updated FE model can accurately simulate the operation of the bridge structure and can be used as the safety performance evaluation and maintenance model of bridge. The method has practical value for engineering application.

concrete continuous girder bridge; finite element;model updating; dynamic testing

2016-04-01；

2016-05-15

国家自然科学基金资助项目(51408393)

张巍(1963—)，男，山西太原人，太原理工大学副教授，工学博士;E-mail: zhangwei_wbl@163.com。

10.13624/j.cnki.issn.1001-7445.2016.1264

U448.23

A

1001-7445(2016)04-1264-07

引文格式：赵崇基，张巍，刘志华,等.基于动力测试的混凝土连续梁桥有限元模型修正[J].广西大学学报(自然科学版)，2016，41(4)：1264-1270.