水泥土桩加固航道边坡稳定性分析

张信贵,许胜才,陆海丽,易念平

(1.广西大学土木建筑工程学院， 广西南宁530004 ；2.广西大学工程防灾与结构安全教育部重点实验室， 广西南宁530004；3.广西防灾减灾与工程安全重点实验室， 广西南宁530004)



水泥土桩加固航道边坡稳定性分析

张信贵1,2,3,许胜才1,陆海丽1,易念平1

(1.广西大学土木建筑工程学院， 广西南宁530004 ；2.广西大学工程防灾与结构安全教育部重点实验室， 广西南宁530004；3.广西防灾减灾与工程安全重点实验室， 广西南宁530004)

水泥土桩作为水平向增强体用于航道土质边坡的加固工程中，加固边坡的稳定性计算没有相关规范参考，目前国内外对水泥土桩加固边坡的稳定性研究也鲜见文献报道。计算分析了水泥土桩加固航道土质边坡的稳定性，结果表明在桩土分算的情况下，极限平衡法计算的安全系数要大于有限单元法计算的结果，而桩土合算的情况下，极限平衡法和有限单元法将得到相同的结论。通过分析认为，桩体发生剪切、弯曲和转动等破坏模式，是极限平衡法与有限单元法计算结果产生差异的根本原因，当涉及土与结构物相互作用时，有限单元法与极限平衡法相比，前者结果更符合实际。水泥土剪力墙加固结构，可以防止桩体产生弯曲、转动等破坏，使加固边坡呈整体剪切破坏模式，有效发挥了水泥土桩的抗剪强度，从而提高边坡的稳定性。

水泥土桩；安全系数；极限平衡法；有限单元法；水泥土剪力墙

0　引　言

航道的建设开发将产生大量软粘土边坡。因边坡高度大，坡线长，采用传统的钢筋混凝土抗滑桩方案工程造价较高。通过深层搅拌法或高压喷射注浆法形成水泥土桩来加固地基在工程建设中得到了广泛的运用。鉴于水泥土施工的方便性与经济性，在边坡的加固技术中也引入了水泥土桩结构，提高粘土边坡的稳定性[1-3]。

水泥土桩加固后的边坡稳定性评价方法，还是一个悬而未决的问题。《公路路基设计规范》[4]中，计算加固土桩复合地基的路堤整体稳定安全系数时，主要是根据面积置换率对桩体和地基土的抗剪强度进行加权平均，再以平均后的抗剪强度对边坡或地基进行稳定性验算，其公式为：

τps=ητp+(1-η)τs,

(1)

式中：τp为桩体的抗剪强度，τs为地基土的不排水抗剪强度，η为桩对土的面积置换率。但是，该规范对水泥土桩复合地基加固边坡的稳定性计算没有给出推荐方法。

在研究方面，Broms等[5]介绍了水泥土桩稳定基坑和边坡的工程特性，并使用复合抗剪强度指标计算加固边坡的稳定性。然而，水泥土桩强度、刚度与桩周土的强度、刚度相差较大，在滑坡推力的作用下，由于桩土之间变形不协调，可能产生剪切、弯曲、转动和拉伸等破坏。Han等[6]、Huang等[7]和Navin等[8-9]通过数值模拟搅拌桩加固路堤下地基的稳定性，发现传统设计中假设桩土发生剪切破坏而求得的安全系数过高估计了路堤的稳定性。郑刚等[10]基于离心模型试验，将路堤下复合地基加固区分为拉弯区、弯剪区、压弯区和承压区4个不同区域，以反映不同区域加固体的阻滑机理。Kivelo[11]和Broms[12]提出对水泥土搅拌桩加固地基进行稳定性分析时，应该把多种破坏模式考虑进去，而不仅仅只是考虑剪切破坏模式，

水泥土桩加固边坡的受力方式与建筑物下的复合地基受力方式不同。单纯在滑坡推力的作用下，桩土之间将发生怎样的破坏模式，且又该如何评价水泥土桩加固边坡的稳定性，目前，缺少这方面的研究资料。因此，本文结合实际工程，对使用水泥土桩加固边坡的稳定性问题，采用极限平衡法和有限单元法分析边坡的稳定性以及两种方法计算结果的差异，为工程实践提供理论参考。

1　算例描述与分析方法

1.1算例描述

图1　水泥土桩加固边坡剖面模型Fig.1　Cross section of slope reinforced by soil-cement columns

为解决通航压力，梧州长洲水利枢纽拟在原有一、二线船闸的基础上，增建三线四线船闸。拟增建船闸的开挖将形成不同断面的高边坡，地层主要有素填土、粘土、全风化花岗岩等不稳定土层。计算表明，部分边坡稳定安全系数不满足设计要求，需要对其进行治理。经过多种方案比较，设计采用高压旋喷桩对边坡进行加固，边坡断面模型如图1所示，其中D表示桩径，S表示桩距，n为桩数。模型中水泥土桩只能被模拟成桩墙，其强度参数可按截面剪切强度等效的方式计算[13]。

1.2分析方法

分别采用极限平衡法和有限元强度折减法[14]分析边坡的稳定性。在极限平衡分析中，采用Morgenstern-Price法，使用的软件是商业化的专业岩土分析软件Geostudio。有限元强度折减法采用大型通用有限元软件Abaqus。边坡模型所有材料均用Mohr-Coulomb模型，模拟过程中均不考虑渗流的影响，材料参数见表1所示。

表1　边坡土层物理力学参数Tab.1　Physico-mechanical parameters of slope soils

2　计算结果对比和分析

2.1桩土分算加固边坡结果对比分析

运用极限衡法计算时，只需改变桩体区域土层参数，把整个边坡当作含复杂土层的边坡进行计算，得到的滑动面如图2所示。同理，在建立有限元模型时，把桩体区域的土层参数改为水泥土桩的强度参数，使用有限元强度折减法计算边坡稳定安全系数，结果如图3和图4所示。由结果可知，极限平衡法得到的加固边坡滑动面为圆弧状，加固后的安全系数是1.62，比未加固情况安全系数(1.20)提高了很多，证明桩体的存在增加了滑动面的抗剪强度。有限元计算的安全系数为1.35，比极限平衡法的结果小。从图3可以看出，由于桩体的存在，边坡失稳时没有形成连续贯通的滑动面，等效塑性应变分布区域比未加固时的大。从图4可知，桩体在滑动土体作用下，产生弯曲变形，破坏时沿桩身形成两个塑性铰，而非形成剪切滑动面。由以上结果可知，两种方法计算桩土分算情况下的边坡稳定安全系数，将会得到不一样的结果。

图2　桩土分算极限平衡法计算结果(Fs=1.62)

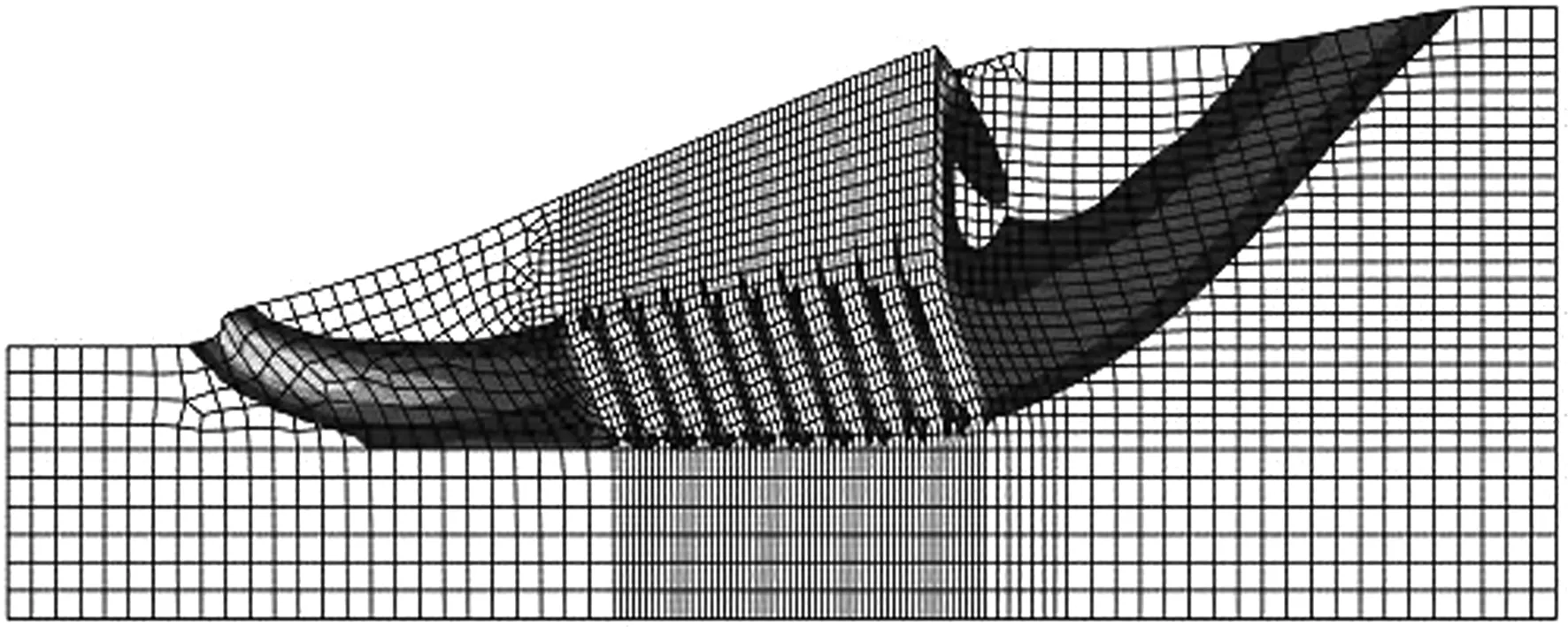
图3桩土分算有限单元法计算结果(Fs=1.35)

Fig.3Results of separated columns model computed by FEM (Fs=1.62)

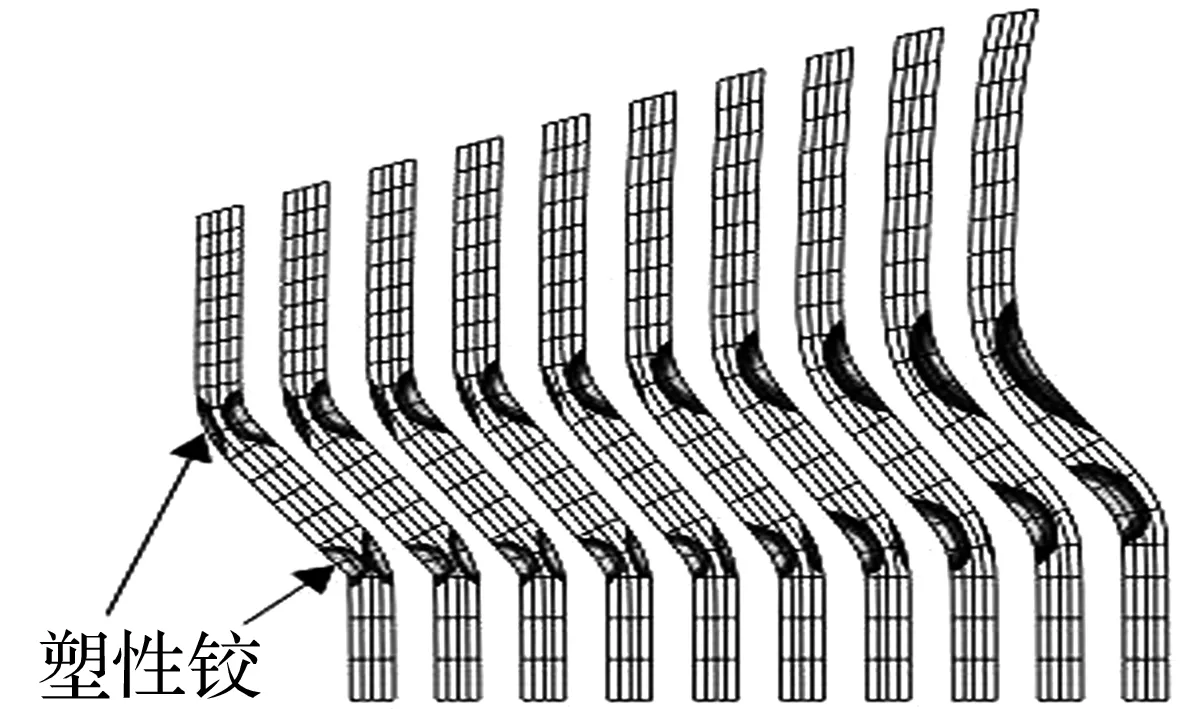
图4有限元强度折减法计算桩体变形图

Fig.4Deformation of columns computed by FEM with strength reductiontechnique

2.2桩土合算加固边坡结果对比分析

桩土分算情况下的稳定性分析，通常会因土层分布过于复杂给极限平衡法和有限单元法的建模带来麻烦，且对边坡进行竖向条分时，也因桩体的存在而给计算造成许多不便。所以，为方便工程设计，对边坡加固区域的土体和桩体进行强度的加权等效，把桩土复合区域变成均质体，其强度参数使用加权等效后的复合强度参数。一般的做法是对桩土的抗剪强度按面积置换率进行加权平均而求得复合强度参数[13]。计算公式如下：

ceq=mcp+(1-m)cs,

(2)

tanφeq=mtanφp+(1-m)tanφs,

(3)

式中：ceq为桩土复合粘聚力，cs为桩间土粘聚力，cp为桩体粘聚力，φeq为桩土复合内摩擦角，φs为桩间土内摩擦角，φp为桩体内摩擦角，m为复合地基面积置换率。

在边坡模型中，加固区域形成类似重力式挡土墙的加固体，计算结果如图5和图6所示。从图5可知，由极限平衡法计算得到的安全系数为1.62，边坡滑动面形状与桩土分算时使用极限平衡法计算的相似，安全系数也几乎相等，滑动面经过了桩土复合区域，相比未加固状态，安全系数提高了很多。图6是有限元强度折减法计算的结果，边坡破坏时也形成了较明显的剪切滑动面，边坡发生剪切破坏，计算得到的安全系数为1.63，与极限平衡法计算结果几乎相等。因此，用复合强度参数计算使边坡土层条件趋向于均质体，从而得出极限平衡法和有限单元法计算结果相等的情况。

图5桩土合算极限平衡法计算结果(Fs=1.62)

Fig.5Results of equivalent area model computed by LEM (Fs=1.62)

图6桩土合算有限单元法计算结果(Fs=1.63)

Fig.6Results of equivalent area model computed by FEM (Fs=1.63)

2.3桩体强度参数变化对加固边坡稳定性影响

对于桩土分算的情况，由于桩土强度参数的差异，导致用极限平衡法和有限单元法得到了不同的结果，因此，探讨桩体的参数变化对边坡稳定性的影响是很有必要的。考虑两种工况，统一保持所有水泥土桩的φ值不变而改变c值和保持c值不变而改变φ值，极限平衡法(LEM)与有限单元法(FEM)计算的安全系数变化规律如图7所示。

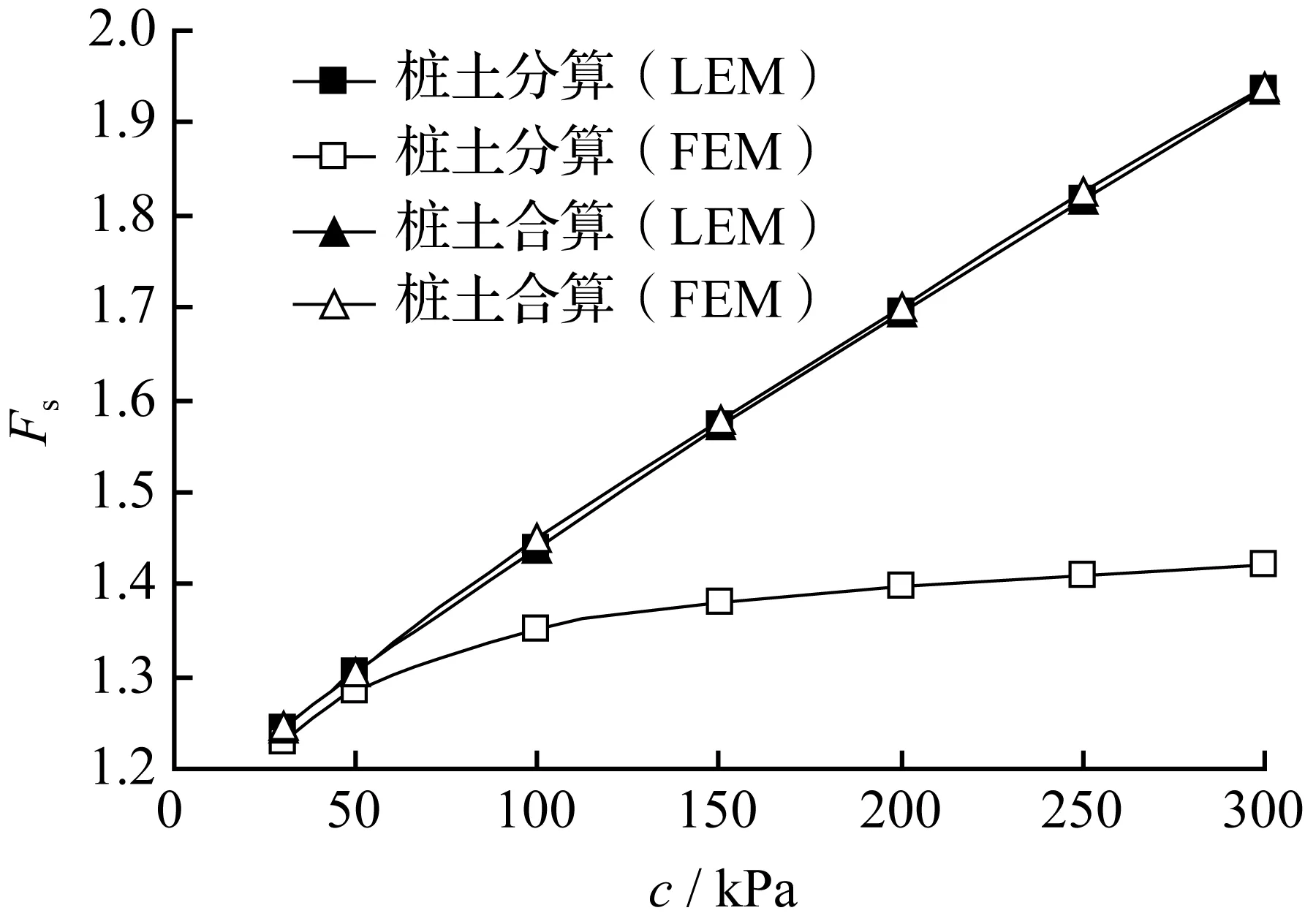
(a) 粘聚力c的影响(ω=14.5°)

(b) 内摩擦角ω的影响(c=85.4 kPa)

图7不同强度参数对应的安全系数变化曲线

Fig.7Changing curves for Safety factors of slope stability with different strength parameters

由图7(a)可知，桩土分算工况下，当桩体材料粘聚力较低时，桩土强度相差较小，边坡类似均质体，这时极限平衡法计算结果与有限单元法的基本相同。随着粘聚力的提高，极限平衡法计算的安全系数几乎是线性增长，而有限单元法计算的却增长较少，并趋于稳定，且当粘聚力超过100 kPa以后，极限平衡法计算的结果远大于有限单元法计算的结果。图7(b)反映了内摩擦角变化对安全系数的影响，当内摩擦角大于15°以后，极限平衡法的计算结果与有限单元法的相差逐渐增大，但差别比粘聚力所造成的稍小。图7还显示了桩土合算工况下，极限平衡法和有限单元法计算的安全系数变化曲线基本重合，反映了在剪切破坏模式情况下，两种方法在分析边坡稳定性时将得到相同的结果。

2.4边坡稳定性计算结果分析

由以上分析可知，用极限平衡法和有限单元法分析边坡的稳定性，得出的结果既有相同之处，也有相异的地方，主要影响因素是边坡破坏模式。

图8　模型箱剪切试验Fig.8　Schematic diagram of the shear box test

当坡体内部存在水泥土桩竖向加固体时，水泥土桩阻挡了滑动面的形成，坡体内部应力分布较复杂。桩土分算的结果表明，具有较大粘聚力的水泥土桩加固边坡后，边坡破坏时桩体内部产生了应力集中，桩周土也较明显出现了塑性滑移，从外观上表现为桩体发生了剪切、弯曲和转动等变形，极限状态下的边坡没能形成一条贯通的剪切滑动面。Larsson等[15]也通过模型箱直剪试验也得到类似结论，如图8所示，本文有限元计算结果与该试验结果不谋而合。极限平衡法假设边坡失稳时只发生剪切破坏，无法反映桩体发生弯曲和转动等破坏的情况，其计算结果往往高估了边坡的稳定性。由于有限元法全面满足静力许可，应变相容以及应力、应变之间的本构关系，揭示了加固边坡内部的破坏本质，更合理地评价了边坡的稳定性。

图5和图6反映了把加固区域按抗剪强度等效为一复合加固体后两种方法的计算结果。复合加固体的长宽比较小，不具备桩体的特征，从有限元的计算结果可知，除部分加固体与土体在接触边界发生塑性滑移外，边坡整体内部最终还是发生了剪切滑动破坏，连续的破坏面贯穿边坡复合加固区域，其破坏形态是和均质土坡一致的。因此，极限平衡法与有限单元法计算这种工况下的边坡时与均质土坡相似，计算结果是相等的。

综上所述，加固边坡中桩体破坏模式的改变是极限平衡法与有限单元法计算结果产生差异的根本原因，当桩体强度逐渐高于桩周土体时，桩体的破坏形式逐渐由单一的剪切破坏发展为剪切、弯曲和转动等破坏形式以及各种破坏形式的组合。

3　水泥土剪力墙加固边坡稳定性分析

由前面分析可知，假设桩土发生剪切破坏模式而充分发挥抗剪强度计算得到的安全系数最高。因此，合理的水泥土桩布桩结构形式应使其抗剪强度得到有效发挥，避免桩体产生拉伸、弯曲及转动等破坏。离散的水泥土桩在受水平荷载作用时容易发生挠曲变形，即使存在多排桩体，也不可能改变这种破坏模式，而且，不同排的桩体还可能产生逐排失效的破坏方式，这种情况下，增加再多的水泥土桩也不能有效提高边坡的稳定性。所以，为使各水泥土桩能联合起来发挥整体的抗剪强度，可以采用桩桩搭接形成墙体结构[16]，本文称之为水泥土剪力墙。水泥土剪力墙加固结构受力方向的抗弯强度较大，可以保证边坡失稳时沿着滑动面产生剪切破坏，有效发挥了水泥土桩的抗剪强度而达到提高边坡稳定性的目的。对于本文算例，水泥土剪力墙加固边坡的结构形式如图9所示，墙体垂直于边坡走向，由剪力墙厚度和宽度换算的面积置换率m与桩土分算时一致，用有限元强度折减法对其稳定性进行分析，计算结果如图10所示。

图9边坡水泥土剪力墙加固结构

Fig.9Shear wall structure of soil-cement for slope

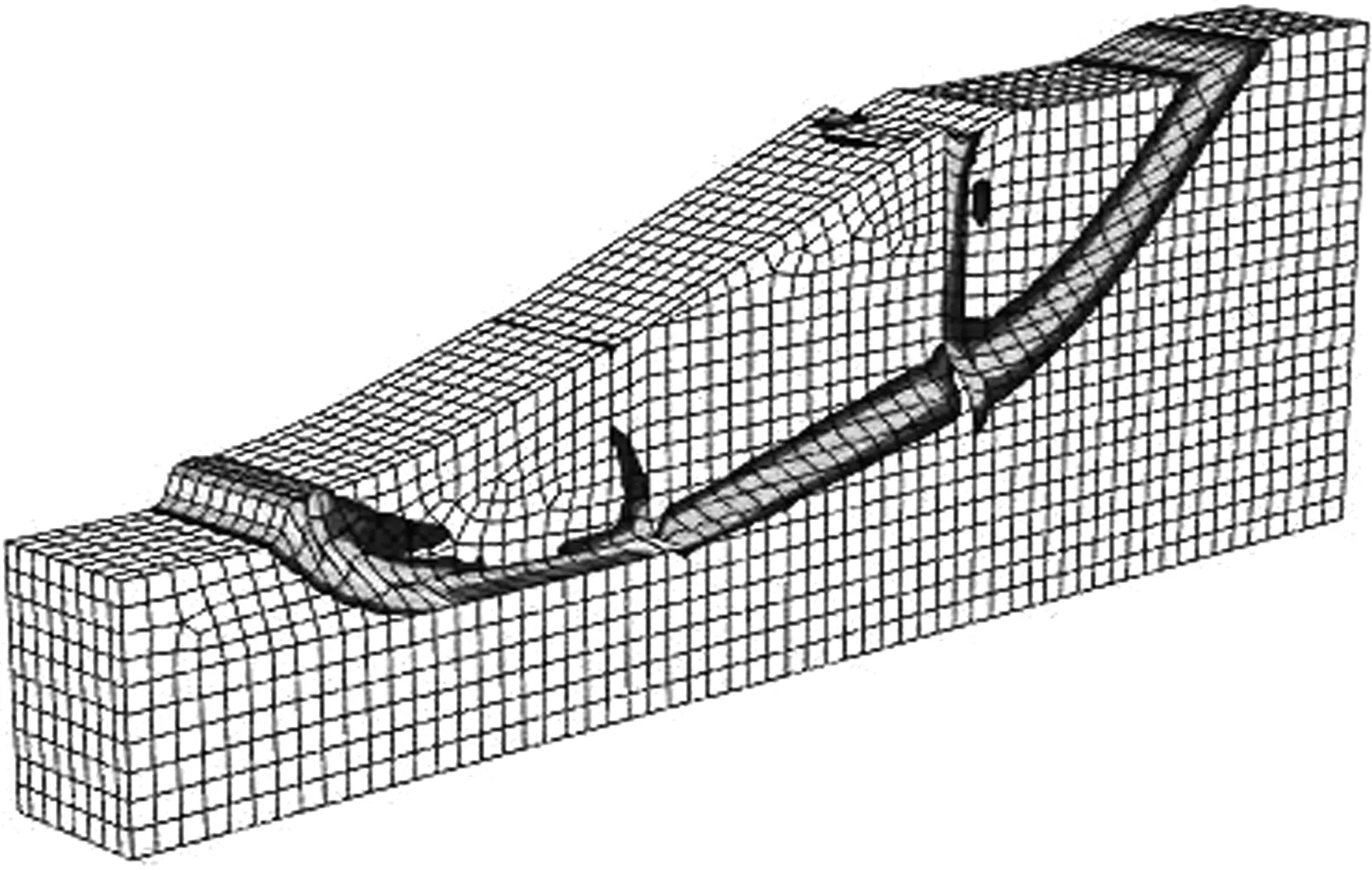
图10边坡稳定计算结果(Fs=1.60)

Fig.10Results of slope stability calculation (Fs=1.60)

由结果可知，剪力墙式水泥土桩加固边坡的稳定安全系数几乎与桩土分算情况下用极限平衡法计算的结果相等。从图10还可以看出，加固区域与土体同时发挥了各自的抗剪强度而发生剪切破坏，等效塑性应变区从坡脚贯通至坡顶，呈连续的圆弧状。剪力墙之间的土体，依靠和墙体接触面的粘结力和摩擦力作用，并未从两墙之间滑移挤出，表明剪力墙对土层起到了加固作用。因此，使用满足Mohr-Coulomb强度准则的材料加固土质边坡时，应选择合理的布桩结构形式，使桩土有效发挥其抗剪强度，从而达到加固的目的。

4　结　语

通过对算例的计算分析，得到如下结论：

①经水泥土桩加固后的边坡，在桩土分算的情况下，极限平衡法计算的安全系数要大于有限单元法计算的结果。有限单元法计算结果表明加固边坡的桩体出现了剪切、弯曲和转动等破坏模式，而极限平衡法计算时只考虑边坡产生剪切破坏。

②将水泥土桩加固区等效为一复合加固体，即桩土合算的情况，此时边坡也类似均质土坡，极限平衡法和有限单元法将得到相同的结论。

③通过桩桩搭接把水泥土桩施工成剪力墙结构形式，在不改变面积置换率的条件下，可以防止桩体产生弯曲、转动等破坏，使边坡呈整体剪切破坏，有效发挥了水泥土桩的抗剪强度，从而提高边坡的稳定安全系数。

④水泥土桩加固边坡，桩体发生弯曲和转动等破坏模式，是极限平衡法与有限单元法计算结果产生差异的根本原因，当涉及土与结构物相互作用时，极限平衡法可能会得出不合理的结论。而有限单元法全面满足静力许可，应变相容以及应力、应变之间的本构关系，结果更符合实际。

[1]徐建周.长洲水利枢纽中江护岸深层搅拌桩施工浅谈[J]. 人民长江，2005, 36(5): 27-28.

[2]于淼,娄吉宏,李春,等.土钉和水泥土搅拌桩复合支护在基坑支护中的运用[J]. 广西大学学报(自然科学版), 2003, 30(3): 221-224.

[3]仲曼,蒋红俊,梁音,等.水泥土连拱抗滑墙加固软基边坡的应用研究[J]. 城市勘测, 2014, 10(5): 167-171.

[4]中华人民共和国交通部.JTGD30—2004公路路基设计规范[S]. 北京：人民交通出版社，2004：66-67.

[5]BROMS B，唐念慈.用石灰及水泥土柱稳定边坡和深开挖[J]. 岩土工程学报，1986，8(6)：18-25.

[6]HAN J, HUANG J, PORBAHA A.2D Numerical modeling of a constructed geosynthetic-reinforced embankment over deep mixed columns[C]// ASCE GSP 131. Austin: Contemporary Issues in Foundation Engineering, 2005.

[7]HUANG J, HAN J, PORBAHA A.Two and three-dimensional modeling of DM columns under embankments[C]//ASCE Geocongress. Atlanta: Geotechnical Engineering in the Information Technology Age, 2006.

[8]NAVIN M P, FILZ G M.Numerical stability analyses of embankments supported on deep mixed columns[C]// ASCE GSP 152. Shanghai: Ground Modification and Seismic Mitigation, 2006.

[9]NAVIN M P, FILZ G M.Reliability of Deep Mixing Method Columns for Embankment Support[C]// ASCE GSP 152. Shanghai: Ground Modification and Seismic Mitigation, 2006.

[10]郑刚,李帅,刁钰.刚性桩复合地基支承路堤稳定破坏机理的离心模型试验[J]. 岩土工程学报, 2012, 34(11): 1977-1989.

[11]KIVELO M.Stabilization of embankments on soft soil with lime/cement columns[D]. Stockholm: Royal Institute of Technology, 1998.

[12]BROMS B B.Can lime/cement columns be used inSingapore and Southeast Asia[R]. 3rd GRC Lecture, Nanyang Technological University and NTU-PWD Geotechnical Research Centre, 1999: 214.

[13]ABUSHARAR S W, HAN J.Two-dimensional deep-seated slope stability analysis of embankments over stone column-improved soft clay[J]. Engineering Geology, 2011, 120: 103-110.

[14]GRIFFITHS D V, LANE P A.Slope stability analysis by finite elements[J]. Geotechnique, 1999,49(3): 387-403.

[15]LARSSON S, BROMS B B.Shear Box model tests with lime/cement columns-some observations of failure mechanisms[C]// Proceedings of the International Conference on Dry Mix Methods. Australia: Melbourne, 2000: 19-24.

[16]IGNAT R, BAKER S, LARSSON S, et al.Two-and three-dimensional analyses of excavation support with rows of dry deep mixing columns[J]. Computers and Geotechnics, 2015, 66: 16-30.

(责任编辑唐汉民梁碧芬)

Stability analysis of channel slope reinforced with soil-cement columns

ZHANG Xin-gui1,2,3, XU Sheng-cai1, LU Hai-li1, YI Nian-ping1

(1. College of Civil Engineering and Architecture,Guangxi University, Nanning 530004, China;2. Key Laboratory of Disaster Prevention and Structural Safety of Ministry of Education,Guangxi University, Nanning 530004, China; 3. Guangxi Key Laboratory of Disaster Prevention and Engineering Safety, Nanning 530004, China)

As a horizontal reinforcement, soil-cement column is used in soil slope reinforcement project of channels. There are no relevant specifications in computing the stability of the reinforced slope for reference. Currently, the researches on stability of the reinforced slope with soil-cement columns are rare both at home and abroad. The stability of reinforced slope with soil-cement columns is calculated and analyzed in this paper. Results show that, under the column-soil separated model, the calculated results from the limit equilibrium method are larger than that from the finite element method, while under the equivalent area model, the results are almost the same. It is thought that failure modes of columns caused by shearing, bending and tilting are the root cause leading to result difference between the limit equilibrium method and the finite element method. When interactions between soil and its structure are involved, the finite element method is more applicable than the limit equilibrium method. The shear wall structure of soil-cement can prevent the columns from failure like bending, tilting and so on, and make the reinforced slope maintain a general shear failure, which having the soil-cement columns play an effective shear-resistance role. Accordingly, the stability of slope is improved.

soil-cement columns; factor of safety; limit equilibrium method; finite element method; shear wall of soil-cement

2016-04-22；

2016-05-18

国家自然科学基金资助项目(51268003;51168005);广西防灾减灾与工程安全重点实验室开放课题(2012ZDK08;2015ZDK001)；广西重点实验室系统性研究项目(2013ZDX11)

张信贵(1965—)，男，广西北流人，广西大学教授，博士生导师；E-mail：xgzhang@189.cn。

10.13624/j.cnki.issn.1001-7445.2016.1067

TU4;TU473.1

A

1001-7445(2016)04-1067-07

引文格式：张信贵,许胜才,陆海丽,等.水泥土桩加固航道边坡稳定性分析[J].广西大学学报(自然科学版)，2016，41(4)：1067-1073.