钢筋混凝土叠合梁受弯承载力可靠度分析

蔡　斌，袁艳慧，赵良龙

(吉林建筑大学土木工程学院， 吉林长春130118)



钢筋混凝土叠合梁受弯承载力可靠度分析

蔡斌，袁艳慧，赵良龙

(吉林建筑大学土木工程学院， 吉林长春130118)

为了研究钢筋混凝土叠合梁受弯承载力可靠度变化规律，提出基于JC法(当量正态化法)的可靠度分析方法。考虑两阶段荷载比值k(第一阶段荷载与第二阶段荷载的比值)和荷载效应比n(可变荷载效应与恒荷载效应的比值)的影响，应用计算软件MATLAB进行数值分析。结果表明：k对叠合梁的可靠度影响很大，当k接近1.0时，叠合梁的可靠度最大；当k增大或减小时，叠合梁抗弯的可靠度均较低；随着n的增大，可靠度降低。当考虑k和n两个因素对受弯承载力可靠度的影响时，随着k的变大叠合梁受弯可靠度先增大后减小，在1.0附近可靠度达到最大值；与单独考虑荷载效应比n不同，此时随着荷载效应比n的增大，可靠度降低。

钢筋混凝土叠合梁；受弯承载力；JC法；荷载效应比；可靠度

0　引　言

叠合构件是由预制混凝土构件(或既有混凝土构件)和现浇混凝土构件组成，即先根据需要预制结构构件，然后在其上浇筑混凝土，形成一种装配整体式结构。这种结构的优点是：相比全预制装配结构其整体刚度和抗震性能更好，而且相比整体现浇结构施工周期短、节省模版材料等。对于叠合结构的研究与应用已有半个多世纪的时间，随着科技的发展越来越多的新型材料和新型组合的出现，给叠合结构领域的扩展带来了契机[1-2]。

叠合构件的应用范围逐渐扩大，对其研究也成为热点，本文考虑将其运用到加固领域，对其加固前后受弯承载力的可靠度进行比较分析。邓志恒、陆春阳[3]对6根连续叠合梁和2根对比梁进行了试验研究，分析结果发现，叠合参数αh(αh=h1/h)较小或第一阶段弯矩与第二阶段弯矩值之比M1/M2较大时，对叠合梁极限承载力的影响很大，设计时为不使叠合梁的抗弯强度比相同条件的整浇梁降低太多，宜保证h1/h>0.4。何大治等[4]对钢筋混凝土叠合受弯构件的极限承载力进行了分析，研究了叠合参数αh、αm(第一阶段荷载产生的弯矩值M1与预制构件的极限抗弯承载力M1u之比)和预制部分混凝土与后浇层混凝土强度比αf对叠合构件受弯极限承载力的影响，结果表明普通整浇梁的极限承载力计算公式仍适用于叠合构件的计算，只是在一些情况下需引入系数进行调整；陈晓强等[5]提出根据不同的荷载效应比，对普通混凝土受弯构件使用阶段变形进行可靠度分析；王磊等[6]对叠合梁受弯特性进行了试验研究，指出叠合层混凝土强度等级比预制混凝土等级高一个级别的构件，其抗弯性能比同一级别的要好；Buonopane、Schafer[7]提出用非线性进行结构分析，可以得到较满意的可靠度。以上研究均未涉及到钢筋混凝土叠合构件受弯承载力的可靠度研究，本文主要研究两阶段荷载比值k和荷载效应比n对叠合梁受弯承载力可靠度的影响。

1　钢筋混凝土叠合梁设计方法

1.1叠合梁荷载取值

根据规范GB50010-2010《混凝土结构设计规范》[8]，不加支撑的叠合受弯构件，按下列两个阶段进行内力计算。

①第一阶段由预制构件承担荷载，因为叠合层混凝土强度未达到设计值，荷载包括本阶段的恒荷载和施工活荷载；

②第二阶段叠合层混凝土已达到设计强度，叠合构件可按整体结构计算；此时荷载考虑下列两种情况并取较大值：

施工阶段：所有构件自重产生的恒荷载以及本阶段的施工活荷载；

使用阶段：所有构件自重产生的恒荷载以及本阶段的使用活荷载。

1.2叠合梁受弯承载力计算公式

叠合梁正截面受弯承载力应按文献[8]计算：

预制构件：

M1=M1G+M1Q，

(1)

叠合构件的正弯矩区段：

M2=M1G+M2G+M2Q，

(2)

其中，M1G为第一阶段结构自重产生的弯矩设计值；M1Q为第一阶段施工活荷载产生的弯矩设计值；M2G为第二阶段面层、吊顶等自重产生的弯矩设计值；M2Q为第二阶段使用活荷载产生的弯矩设计值，活荷载取施工阶段活荷载和使用阶段活荷载的较大值。

文献[8]中混凝土强度等级的取用方法：正弯矩区段按叠合层取用、负弯矩区段按计算截面受压区的实际情况取用。但在计算正截面受弯承载力时，为了安全起见混凝土强度等级取预制构件和叠合层中较低的强度等级。

2　极限状态功能函数的建立

2.1极限状态方程的建立

极限状态功能函数是根据GB50068-2011《建筑结构可靠度设计统一标准》[9]中的规定来建立的：

Z=g(X1,X2,…,Xn)=0,

(3)

其中：g(·)为功能函数；Xi(i=1,2,…,n)为作用在结构上的各种荷载、材料的性能以及几何参数等基本变量。由于基本变量存在一定的不确定性，应将其作为随机变量考虑。

当仅考虑两个基本变量(即结构所承受的作用效应S和结构本身所具有的抗力R)时，极限状态方程见下式：

Z=R-S=0。

(4)

2.2确定功能函数

结构构件的可靠度用可靠度指标β来表示，可靠度的计算在随机可靠性理论的前提下，采用分项系数表达的概率极限设计方法，本文运用考虑基本变量概率分布类型的一次二阶矩法进行计算。

叠合梁第一阶段可靠度计算时的功能函数：

Z=R-S=fyAs(h01-0.5x1)-M1G-M1Q，

(5)

式中：R=M1u=α1fcbx1(h01-0.5x1)=fyAs(h0-0.5x1)，其中α1的取值当混凝土强度等级不超过C50时，取1.0； 混凝土等级为C80时，取0.94，其间按线性内插法求得。M1G为第一阶段恒荷载q1GK产生的弯矩效应平均值，M1Q为第一阶段可变荷载q1QK产生的弯矩效应平均值。

叠合梁第二阶段可靠度计算时的功能函数：

Z=R-S=fyAs(h0-0.5x)-M1G-M2G-M2Q，

(6)

式中：M2G为第二阶段恒荷载q2GK产生的弯矩效应平均值，M2Q为第二阶段可变荷载q2QK和第一阶段可变荷载q1QK最大值产生的弯矩效应平均值。当Z>0时，构件处于安全可靠状态；当Z<0时构件处于不安全状态；当Z=0时构件处于极限状态。

3　设计参数统计特征以及可靠度分析流程

3.1设计参数的统计特征

康奈尔[10]提出的一次二阶矩法计算模式，结构可靠性理论基本完善。根据结构可靠度设计方法，基于JC法(当量正态化法)应用科学计算软件MATLAB对结构可靠度进行计算。本文采用JC法编制程序时需要用到各随机变量的统计特征，随机变量的统计特征是通过对大量的数据进行统计计算，最后得到变量的统计平均值和标准差[11]。其中，涉及到的主要变量有：混凝土抗压强度、钢筋抗拉及抗压强度、钢筋截面面积、恒荷载和可变荷载、截面的有效高度和截面宽度等参数，根据文献[11-13]采用各参数的统计特征情况列于表1。

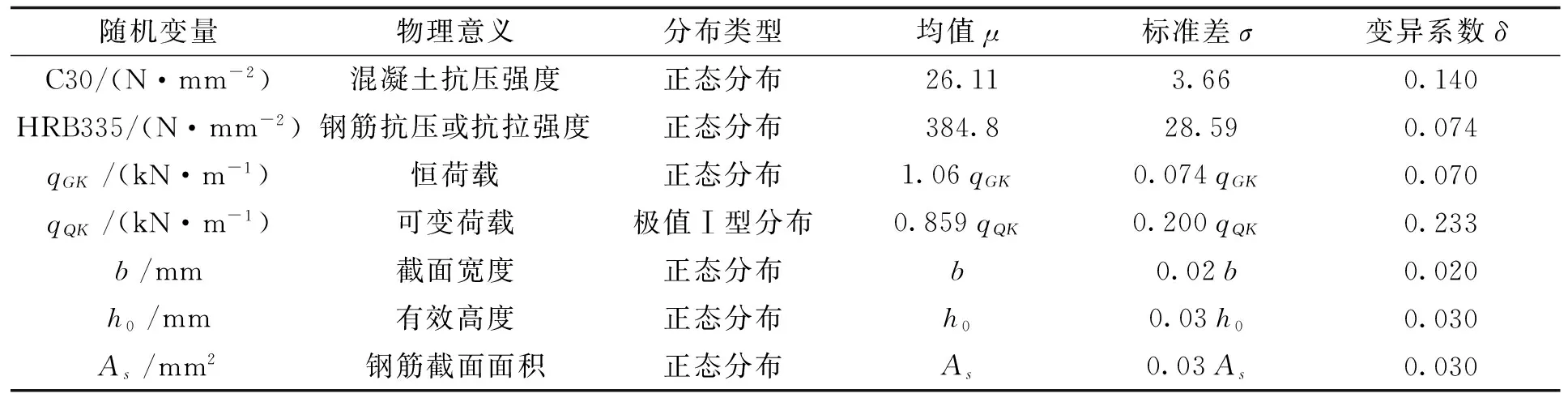
表1　各随机变量的统计参数Tab.1　Statistical parameters of random variables

3.2可靠度分析方法流程

中心点法和基本验算点法都属于一次二阶矩法。中心点法没有考虑随机变量的概率分布，计算结果粗糙，比较适合计算要求精度不高的问题；而基本验算点法虽然考虑了随机变量的概率分布，但其只能解决正态分布变量求解问题；JC法可以处理其他概率分布的变量问题[14-15]。因此，本文采用JC法求解叠合梁受弯极限状态承载力的可靠度，具体流程:

①根据算例所给荷载条件：可变荷载和永久荷载的标准值qGK和qQK，按公式(1)和(2)计算构件的弯矩作用效应设计值MG和MQ；

②根据弯矩承载力的设计值MG和MQ，设计叠合构件纵向配筋As；

③根据公式(5)和(6)建立功能函数Z=R-S=fyAs(h0-0.5x)-MG-MQ，确定功能函数中各变量的统计参数，即均值和变异系数等，为软件的编程做准备；

④根据文献[15]和[16]编制计算程序，通过软件MATLAB计算出结构的可靠度指标β；

⑤在给定的荷载效应比n情况下，改变第一阶段和第二阶段荷载的大小，求解不同k所对应的可靠度指标β；改变恒荷载和活荷载的值，重复以上步骤，求解不同的荷载效应比n对应的可靠度指标β。

4　叠合梁受弯可靠度的算例分析

4.1算例

已知一钢筋混凝土叠合梁为简支梁，梁截面为矩形。梁宽b=250 mm，预制梁的高度为h1=500 mm，计算跨度l0=5 800 mm，混凝土采用C30，相应的fc=14.3 N/mm2，α1=1.0，ft=1.43 N/mm2；叠合梁高h=700 mm，叠合层混凝土采用C25(fc=11.9 N/mm2，α1=1.0)。受拉纵向钢筋采用HRB335(fy=300 N/mm2)，箍筋采用HPB300钢筋(fy=270 N/mm2)，施工阶段不加支撑。

第一阶段预制梁承受恒荷载(预制梁、板及叠合层自重)标准值q1GK，可变荷载(施工阶段)标准值q1QK；第二阶段恒荷载(面层、吊顶自重等新增恒荷载)标准值q2GK，第二阶段施工活荷载与第一阶段施工活荷载相等[17]，使用阶段活荷载标准值q2QK。

4.2叠合构件加固前后的可靠度计算

对于老旧建筑不能满足强度要求或使用要求，或者新建建筑设计出现问题不能满足受力或变形要求，均可以在原有构件上叠合新的构件，以使构件满足要求。

用JC法计算加固前可靠度指标β1为3.781 9，加固后的可靠度指标β2为3.856 3，很明显加固后构件的承载能力增加一倍多，加固后的可靠度指标β2也比加固前的β1大。结果表明叠合加固后的可靠度符合相关规定，并相对于加固前的可靠度指标有所提高。

4.3两阶段荷载比值k(k=q1/q2)对可靠度的影响

叠合构件受力较普通梁有所差异，第一阶段与第二阶段荷载比值不同对结构承载力的可靠度有很大的影响。取第一阶段荷载与第二阶段荷载比值为k，其中k分别取0.5、0.67、1.0、1.5、2.0五个值，第一阶段荷载与第二阶段荷载总值为60 kN/m，设恒荷载与可变荷载的取值相同，即荷载效应比n=1.0。在对叠合梁计算时，恒荷载取第一阶段恒荷载和第二阶段恒荷载之和，活荷载取施工阶段活荷载和使用阶段活荷载的最大值，设第一阶段活荷载等于第二阶段施工荷载，构件的纵向钢筋配置为4Φ20，且钢筋的配筋率均大于文献[18]计算的最小配筋率，小于文献[19]计算出来的最大配筋率，荷载标准值的具体取值情况如表2所示。

表2　荷载取值情况Tab.2　Load values　kN·m-1

注：1.“恒+活”含义为“第一阶段恒荷载+第二阶段恒荷载+最大值(第一阶段活荷载，第二阶段活荷载)”。

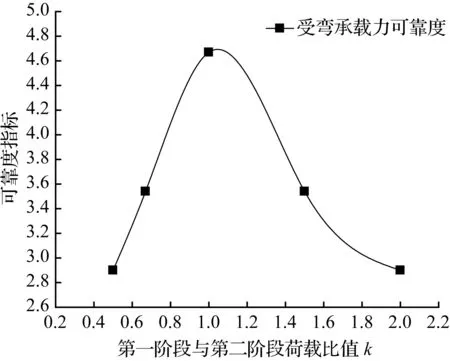
图1　可靠度指标与第一阶段和第二阶段荷载比值k关系Fig.1　Reliability index’s relationship with the ratio of first stage of the load and the second’s

表2中叠合构件承受的总荷载保持不变，两阶段荷载比值k不管为多少，由于荷载效应比为1.0，所以结构的恒荷载一直保持30 kN/m不变，活荷载取两阶段活荷载的最大值。通过软件MATLAB编程计算可靠度，则其可靠度指标计算结果见图1。

从图1中可以看出，第一阶段与第二阶段荷载比值k从0.5升高到2.0，说明第二阶段承受的荷载逐渐减小，可靠度先升高然后降低，在两阶段荷载比值为1.0时的可靠度最高，结构最安全；随着两阶段荷载比值k的变大，其可靠度指标分别取值为：2.90、3.54、4.67、3.54、2.90，其平均值为3.51，满足二级安全等级要求。

4.4荷载效应比对可靠度的影响

荷载效应比为活荷载效应与恒荷载效应比值，令恒荷载和活荷载的总和保持不变为50 kN/m，研究荷载效应比对叠合构件可靠度的具体影响，对叠合构件进行弯矩计算时取第一阶段可变荷载和第二阶段可变荷载的较大值，其荷载取值如下：

①qQK=16.7 kN/m，qGK=33.3 kN/m，n=0.5；②qQK=25 kN/m，qGK=25 kN/m，n=1.0；

③qQK=27.8 kN/m，qGK=22.2 kN/m，n=1.25；④qQK=30 kN/m，qGK=20 kN/m，n=1.5；

⑤qQK=33.3 kN/m，qGK=16.7 kN/m，n=2.0；⑥qQK=37.5 kN/m，qGK=12.5 kN/m，n=3.0。

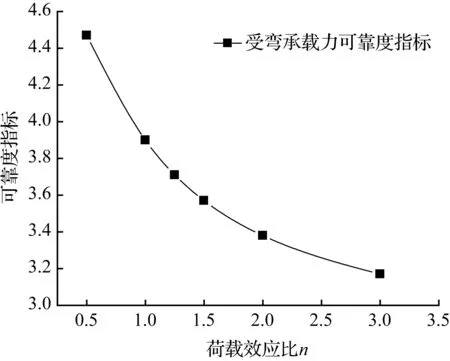
图2　可靠度指标与荷载效应比的关系Fig.2 The relationship between reliability and load effect ratio

计算过程中的具体数值与算例相同，但钢筋配置为2Φ22+2Φ20。经过计算得出可靠度指标与荷载效应比的一组关系如图2所示。

图2表明，荷载效应比为0.5时，可靠度指标为4.47；荷载效应比为1.0时，可靠度指标为3.9；荷载效应比为1.25时，可靠度指标为3.71；荷载效应比为1.5时，可靠度指标为3.57；荷载效应比为2.0时，可靠度指标为3.38；荷载效应比为3.0时，可靠度指标为3.17。荷载效应比从0.5增加到3.0时，活荷载所占的比例变大，可靠度相应减小。

分析图2中的具体情况如下:

①荷载效应比从0.5到3.0，可靠度呈现非线性减小；

②在所研究的数据中，当荷载效应比为0.5时对应的可靠度最大，达到一级安全等级的要求；

③从几组数据的可靠度结果可以看出，可靠度指标平均值为3.7，满足结构的安全性能和相关规范要求。即使在荷载效应比为3.0时的可靠度指标仍为3.17，依然满足延性破坏三级安全等级的破坏要求。

4.5考虑两阶段荷载比值和荷载效应比两因素对可靠度的影响

单独考虑两阶段荷载比值得到的结论是：当两阶段荷载比值为1.0时的可靠度最高；单独考虑荷载效应比时得到的结论是：荷载效应比越小，结构的可靠度越大。考虑这两个变量因素(两阶段荷载比值k和荷载效应比n)对可靠度的影响，两阶段荷载比k分别取值0.5、0.7、0.9、1.1、1.3、1.5，荷载效应比n分别取值0.25、0.5、1.0、1.25。第一阶段与第二阶段所有荷载总值不变为60 kN/m，钢筋配置为4Φ20，荷载效应比n确定后，结构所受的恒荷载取值确定qG=60/(n+1)，而活荷载取值：

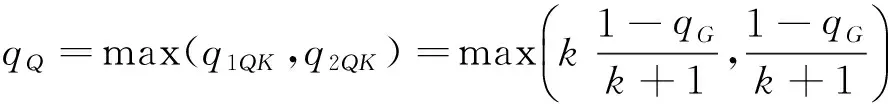
(7)

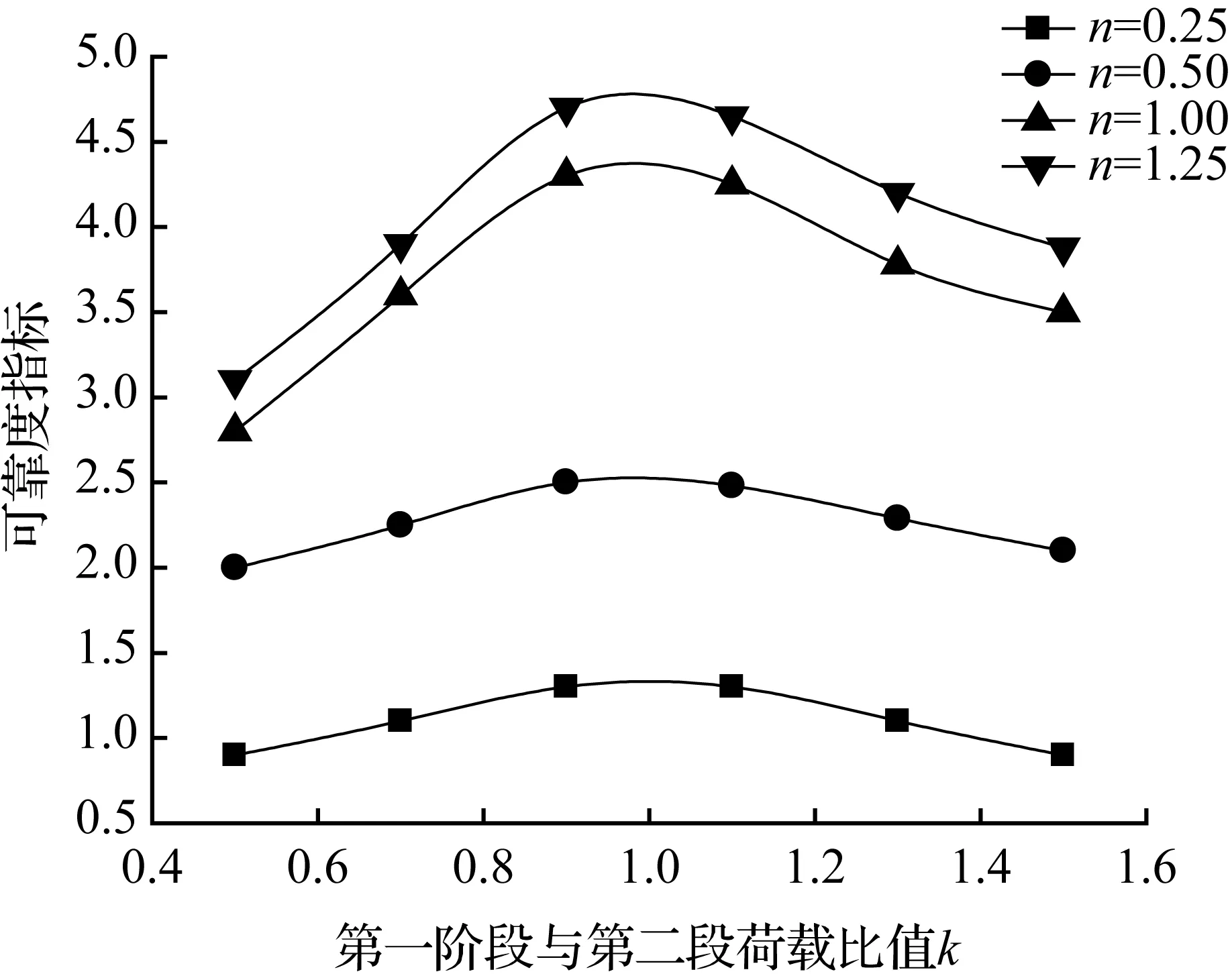
图3　荷载效应比和两阶段荷载比对可靠度指标的影响Fig.3　Effect of load effect ratio and two-stage load ratio on reliability

则计算得到的可靠度指标如图3所示。

从图3可知，第一阶段与第二阶段荷载比值k在1.0附近时，叠合梁的可靠度最高，远离1.0荷载逐渐减小；荷载效应比n越大，叠合梁的可靠度越大，这与单独考虑荷载效应比对叠合梁受弯可靠度的影响截然相反。这是因为：随着荷载效应比变大，恒荷载变小，活荷载变大，且活荷载取第一阶段与第二阶段活荷载较大值，较小值舍弃，舍弃的活荷载和恒荷载的变小导致叠合梁承受的总荷载标准值减小，使得可靠度增加。

5　结　论

本文计算了几组叠合梁的可靠度指标β，并分析影响它的两个因素：两阶段荷载比值k和荷载效应比n，主要得出如下几个结论：

①叠合构件加固后随着抗弯承载力的提高，抗弯承载力可靠度也有所提高，但是提高幅度很小。

②两阶段荷载比值k对叠合梁的可靠度影响很大，两阶段荷载比值较大或较小时，叠合梁抗弯承载力的可靠度较小；两阶段荷载比值k在1.0附近时，叠合梁的抗弯承载力可靠度较大。

③随着荷载效应比n增大，可靠度指标β减小。这是因为可变荷载服从极值Ⅰ型分布，荷载效应比增大时，可变荷载逐渐增大，其变异性比恒荷载大，变异性越大对结构越不利。

④当两阶段荷载比值相同时，叠合梁受弯承载力的可靠度随着荷载效应比的增大而增大，这是因为构件承受的总荷载标准值减小的缘故；当荷载效应比相同时，叠合梁的可靠度随着两阶段荷载比值的增加先增大后减小，在两阶段荷载比值为1.0时，可靠度取得最大值。

[1]赵顺波，张新中.混凝土叠合结构设计原理与应用[M]. 北京：中国水利水电出版社，2001：5-10.

[2]周旺华.现代混凝土叠合结构[M]. 北京：中国建筑工业出版社，1998:1-7.

[3]邓志恒，陆春阳.钢筋砼二次受力叠合梁正截面强度试验研究[J]. 广西大学学报(自然科学版)，1993,18(3):58-62.

[4]何大治，张宗敏，张多新.混凝土叠合式受弯构件极限承载力分析[J]. 河南科学，2010，28(6)：709-712.

[5]陈晓强，汲雨林.混凝土受弯构件挠度与裂缝计算公式的可靠度分析[J]. 武汉科技大学学报(城市科学版)，2004,15(2)：84-87.

[6]王磊，彭笑川.叠合梁受弯性能试验研究[J]. 建筑结构，2013，43(8)：51-53.

[7]BUNONOPANE S G, SCHAFER B W.Reliability of steel frames designed with advanced analysis[J]. Journal of Structural Engineering,2006,132(2):267-276.

[8]中华人民共和国住房和城乡建设部.混凝土结构设计规范：GB50010-2010[S]. 北京：中国建筑工业出版社，2010.

[9]中华人民共和国住房和城乡建设部.建筑结构可靠度设计统一标准： GB50068-2011[S]. 北京:中国建筑工业出版社，2011.

[10]CORNELL C A.Probability based structural code[J]. Journal of American Concrete Institute, 1969,66(12):974-985.

[11]邵仕萍.AFRP加固钢筋混凝土梁受弯性能试验研究及可靠性分析[D]. 长春：吉林建筑大学，2015.

[12]黄炎生，宋欢艺，蔡 健.钢筋混凝土偏心受压构件增大截面加固后可靠度分析[J]. 工程力学，2010,27(8):146-151.

[13]蔡斌.钢筋混凝土可靠度计算的若干问题[D]. 长春：吉林大学，2011.

[14]赵国藩,金伟良,贡金鑫.结构可靠度理论[M]. 北京:中国建筑工业出版社, 2000:10-28.

[15]张明.结构可靠度分析——方法与程序[M]. 北京:科学出版社, 2009:1-65.

[16]ZHAO Y G .A general procedure for first/second-order reliability method (FORM/SORM)[J]. Structural Safety, 1999, 21(2): 95-112.

[17]国振喜.简明钢筋混凝土结构计算手册[M]. 北京：机械工业出版社，2012:1325-1345.

[18]龙炳煌.叠合梁的最小配筋率及设计建议[J]. 工程力学，1998(增刊2)，366-370.

[19]龙炳煌，周旺华.混凝土叠合梁的界限受压区高度和最大配筋率公式[J]. 土木工程学报，1994,27(6):16-19.

(责任编辑唐汉民梁健)

Reliability analysis on flexure capacity of reinforced concrete composite beam

CAI Bin, YUAN Yan-hui, ZHAO Liang-long

(School of Civil Engineering，Jilin Jianzhu University, Changchun 130118，China)

In order to study the reliability of flexure capacity of reinforced concrete composite beams, a reliability analysis method based on JC method (equivalent normalized method) is proposed.k(the load ratio of the first stage to the second stage) andn(the ratio of live load effect to dead load effect) are considered to perform the numerical analysis with the computational software MATLAB. Results show thatkhas a great influence on the reliability of composite beam. Whenkis close to 1.0, the reliability of bending of composite beam is the largest. But whenkis larger or smaller, the reliability of bending of composite beam is lower. With the increase ofn, the reliability decreases. When considering the effect of bothkandnon the flexure capacity reliability, the authors find that the bending reliability of composite beam first increases, then decreases with the increase ofk. Whenkis near 1.0, the reliability also reaches the maximum. The reliability is higher with the increase of load effect ration.

reinforced concrete composite beam; bending capacity; JC method; load effect ratio; reliability

2015-12-24；

2016-05-26

国家自然科学基金资助项目(51178206)

蔡斌(1978—),男，吉林长春人，吉林建筑大学副教授，博士；E-mail： caibin@jliae.edu.cn。

10.13624/j.cnki.issn.1001-7445.2016.0992

TU375.1

A

1001-7445(2016)04-0992-07

引文格式：蔡斌，袁艳慧，赵良龙.钢筋混凝土叠合梁受弯承载力可靠度分析[J].广西大学学报(自然科学版)，2016，41(4)：992-998.