不确定时延网络控制系统的稳定性设计

杨新伟，郭彩霞

（河南师范大学 物理与电子工程学院，河南 新乡　453007）

不确定时延网络控制系统的稳定性设计

杨新伟，郭彩霞

（河南师范大学 物理与电子工程学院，河南 新乡453007）

摘要：针对网络环境下的控制系统所具有的网络时延和不确定性特点，考虑最大允许网络诱导时延下界不为零及系统带有不确定性的情况，采用不需事先指定参数的更具一般性的状态反馈控制器，建立状态反馈的闭环网络控制系统模型。通过引入积分不等式方法，对Lyapunov⁃Krsasovskii泛函中的二次型积分项直接进行界定，避免了对系统进行模型变换和对交叉项的界定所带来的保守性。在此基础上，推导出使网络控制系统鲁棒稳定的条件。最后通过对模型进行Matlab仿真，得到状态响应曲线。系统状态很快趋于稳定，表明该结论的有效性和可行性。

关键词：网络控制系统；网络诱导时延；积分不等式方法；Lyapunov⁃Krasovskii泛函

0　引　言

随着计算机与信息技术、网络技术与控制理论的发展，网络控制系统（NCS）被广泛应用于航空航天、传感器网络、工业控制网络、机器人远程控制和微机电系统等复杂的控制系统中［1⁃8］。然而，通信与控制的相互作用使NCS的分析和设计变得非常复杂。基于网络的控制系统给信号处理、通信技术和控制技术等提出了新的挑战。近年来，众多学者对NCS的研究非常活跃，如NCS的稳定性分析与控制综合、最大时延上界的求取等，它们统称为基于网络的控制，也被确定为控制领域的关键研究方法之一［9］。

网络时延是导致NCS性能下降的主要原因，同时，系统建模误差和工作环境的变化也导致系统存在不确定性，因此，考虑具有网络时延和不确定性的NCS的分析和设计是当前研究的热点［6，10］。文献［9］将NCS中诱导延时、丢包和数据包错序等问题表示成最大允许时延的NCS综合模型，考虑外界扰动下不确定性系统的鲁棒分析和综合问题。但是在系统综合分析时，必须事先指定一些参数，且这些参数只能采用试凑的方法，因此给系统带来很大的保守性。

文献［11］中为了处理上的方便，在构造Lyapunov⁃Krasovskii泛函时，利用牛顿⁃莱布尼茨公式对泛函中的双积分项进行了模型变换，变换的目的是产生积分项，使得交叉项和二次型积分项同时出现，对交叉项的界定抵消泛函导数中的二次型积分项，获得了时延相关的系统稳定条件；但是，此变换将导致变换后的系统产生新的动态而与原系统不等价，使得系统结果变得保守［9］。文献［12］把数据包丢失情况作为不确定性处理，考虑网络时延有上界，并通过引入自由权矩阵消除了交叉项，但是自由权矩阵的引入会需要耗费更多的计算机运行时间。

本文考虑最大允许网络诱导时延下界不为零及系统带有不确定性的情况，并采用更具一般性的状态反馈控制器。引入积分不等式方法，通过对泛函中的二次型积分项直接进行界定，避免了对系统进行模型变换和对交叉项的界定所带来的保守性，推导出使闭环网络控制系统的鲁棒稳定性条件。

1　NCS问题描述

考虑被控对象具有时变结构不确定性，可表示为如下状态方程：

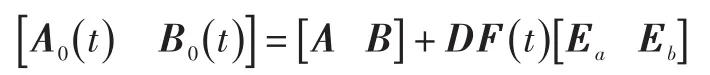
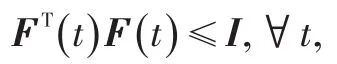
为方便分析，先做如下假设：传感器采用时钟驱动方式，而控制器采用事件驱动方式，T为采样周期。传感器在采样时刻0，T，2T，…，nT都采样数据并给数据包打上时间标签向控制器发送，如图1所示。

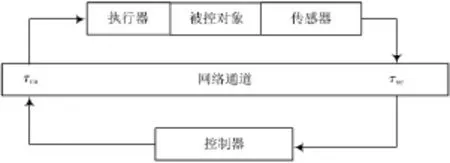
图1　网络控制系统结构框图

经过网络时延τsc后，控制器收到数据后立即进行计算，控制器计算时间为τc，计算出控制信号后向执行器发送，经过网络时延τca后控制信号到达执行器，在此过程中始终保持系统时钟同步。采用状态反馈控制器：

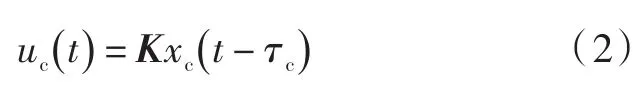
则可知执行器收到的控制信号为：

假定网络时变时延τ=τsc+τc+τca≤γ，γ是从传感器到执行器之间的网络诱导时延上界。综合式（1）～式（3），网络控制闭环系统就可表示为：

2　NCS鲁棒稳定性分析

为了对闭环系统进行稳定性分析，引入几个定理：

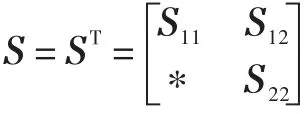
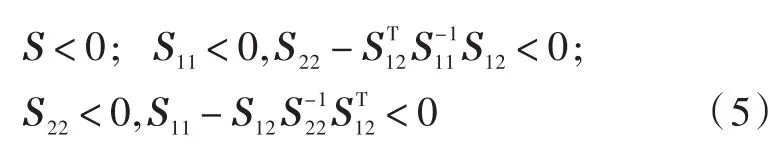
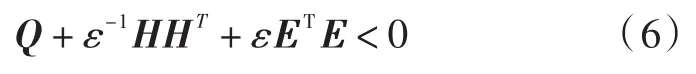
Park不等式［12］：对任意给定向量 α，b∈Rn，矩阵M∈Rn×n，则以下不等式成立：

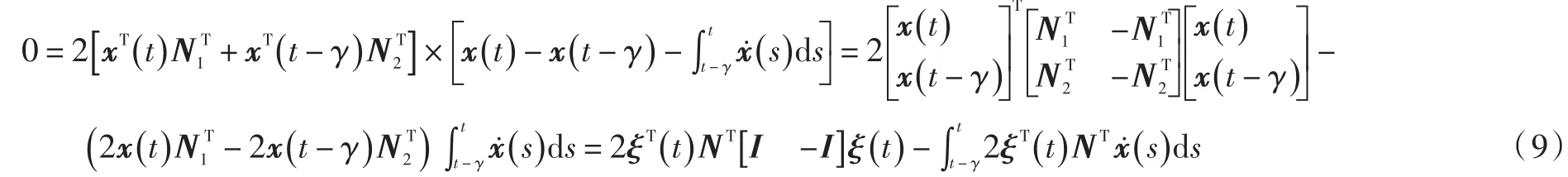
应用Park不等式，有：

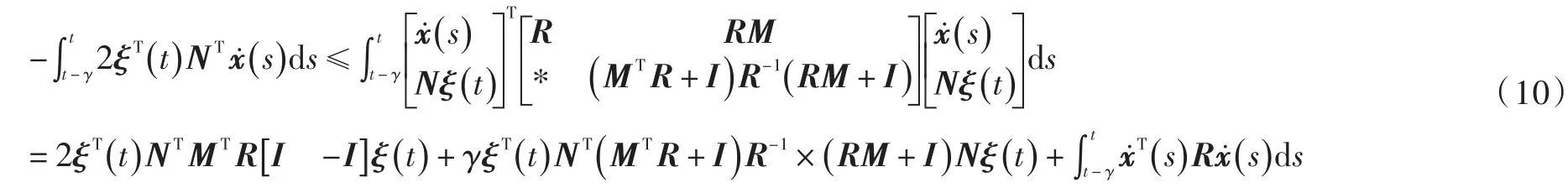
将式（10）代入式（9）可得：

对于NCS构造如下形式的Lyapunov⁃Krasovskii泛函：

式中，P=PT＞0，R=RT＞0是待定矩阵。

计算V（t，xt）沿系统（4）的导数，并由式（4）和式（13）可得：

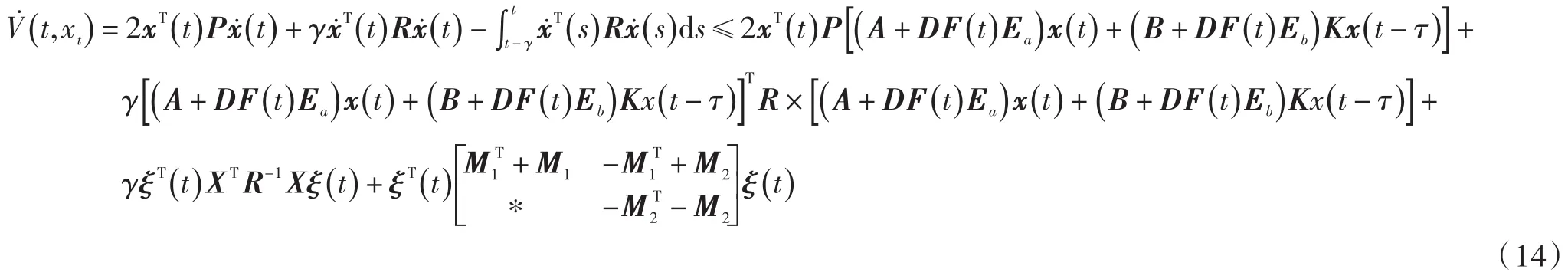
将式（14）整理得：

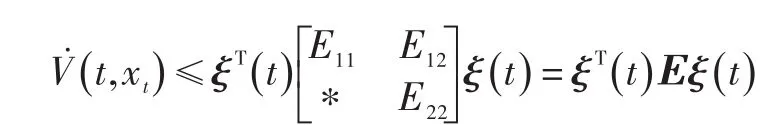
式中：

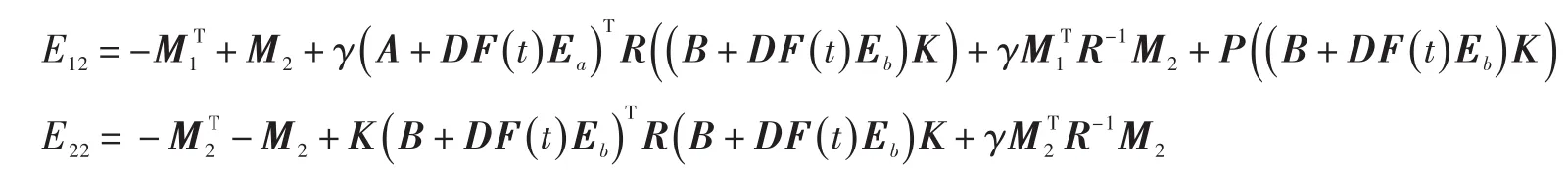
若Ε＜0可解，则由Lyapunov⁃Krasovskii稳定性定理知，闭环NCS式（4）是渐进稳定的。

两次利用Schur补引理，Ε＜0等价于:

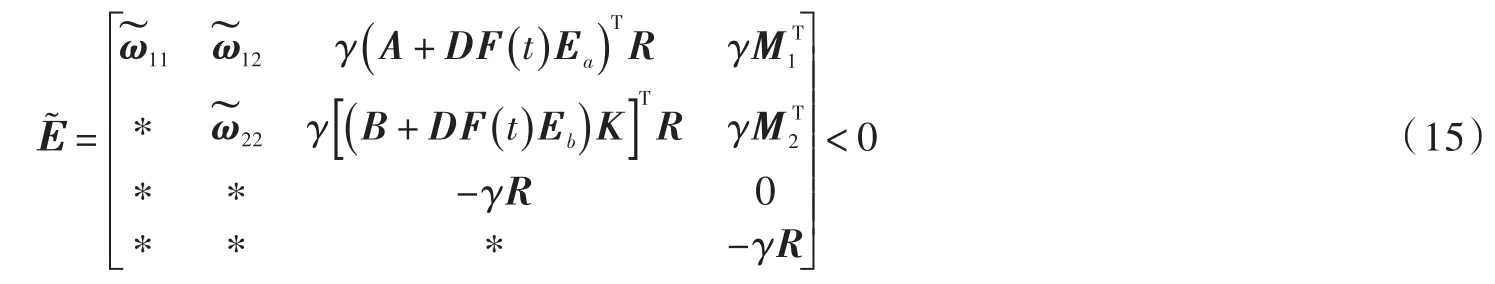
式中:

式（15）可整理为:

由引理2，若存在标量ε＞0，则满足:

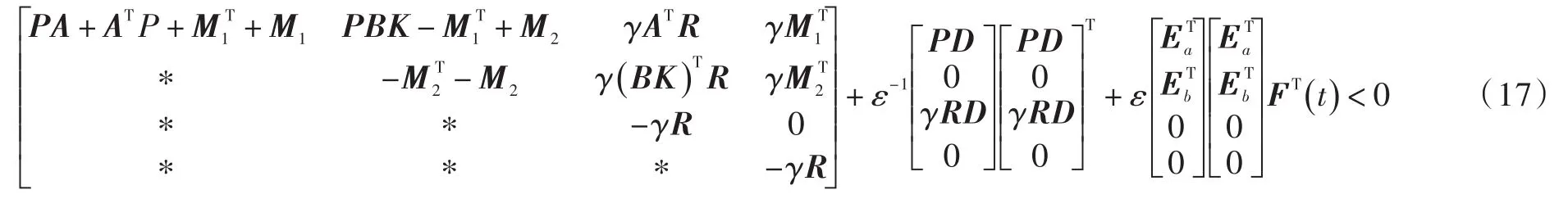
即得:

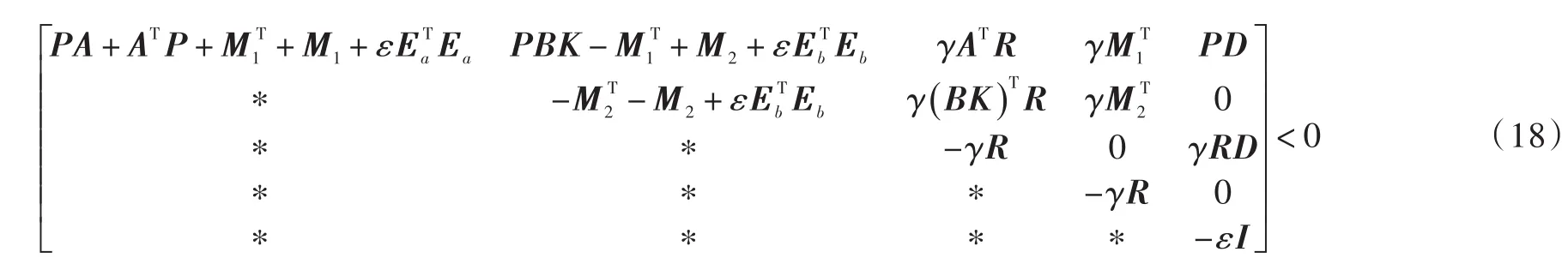
再次利用Schur补引理，可得式（18）等价于式（8）。

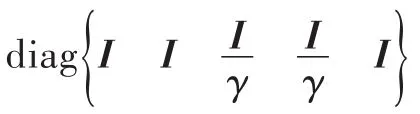
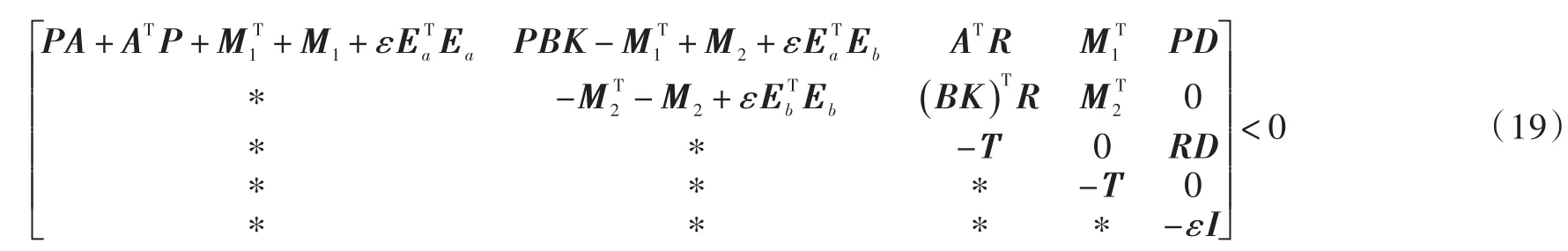
且有：

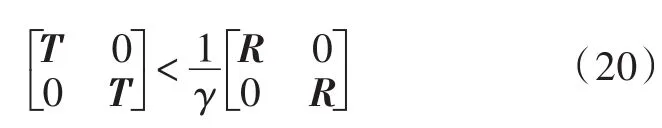
即可用求解器gevp求得最大时延上界。

3　系统仿真

用Matlab的 gevp求解器可得最大时延上届γ=3.028，即时延0≤τ≤0.330 2。

取ε=1，γ=0.3，h=0.2，用feasp求解器验证可行性，可得tmin=-0.035 9，正定矩阵：

矩阵：

系统的状态响应曲线如图2所示，从图2中可以看出，系统状态很快趋于稳定。

4　结　论

本文针对具有时变时延和不确定性的网络化控制系统，通过引入积分不等式方法，对Lyapunov⁃Krsaso⁃vskii泛函中的二次型积分项直接进行界定，避免了对系统进行模型变换和对交叉项的界定所带来的保守性，推导出使网络化控制系统鲁棒稳定的条件。并给出满足闭环系统稳定条件下的最大允许时延上界的求取方法，最后的仿真算例表明了该结论的有效性和可行性。

图2　网络闭环控制系统的状态响应曲线

参考文献

［1］康科飞.基于不确定非线性智能电网感知网络控制系统方法研究［J］.现代电子技术，2014，37（21）：139⁃141.

［2］程满玲，孙峙华.基于BP神经网络技术的网络时延预测研究［J］.现代电子技术，2015，38（23）：28⁃30.

［3］张芳，吴斌，季晓静，等.网络控制系统仿真平台的研究［J］.现代电子技术，2008，31（6）：90⁃92.

［4］李炜，王艳飞.少保守性网络化控制系统鲁棒保性能容错控制［J］.兵工学报，2012，33（2）：170⁃178.

［5］李同涛，邓丽，费敏锐，等.一类带有随机、有界时滞网络控制系统的脉冲控制［J］.控制与决策，2013，28（2）：294⁃298.

［6］游科友，谢立华.网络控制系统的最新研究综述［J］.自动化学报，2013，39（2）：101⁃118.

［7］MAO Zehui，JING Bin，PENG Shi.Observer⁃based fault⁃tolerant control for a class of netwotrked control systems with transfer delays［J］.Journal of the Franklin Institute，2011，348：763⁃776.

［8］胥吉林，屈百达，徐保国.不确定时延网络控制系统的保性能控制［J］.计算机工程与应用，2014，50（5）：239⁃242.

［9］彭晨，田恩刚.一种改进的具有非理想网络状况的网络控制系统分析与综合方法［J］.自动化学报，2010，36（1）：188⁃192.

［10］张先明.基于积分不等式方法的时滞相关鲁棒控制研究［D］.长沙：中南大学，2006.

［11］HUAI C Y，XIN H，MIN W，et al.Delay⁃dependent stability criteria for a class of networked control systems with muti⁃input and muti⁃output［J］.Chaos solitions&fractals，2007，34：997⁃1005.

［12］WEI Lisheng，FEI Minrui.New delay⁃dependent stabilisation criterion for a class of networked control systems［J］.Computer Application in Technology，2012，43（1）：29⁃35.

中图分类号：TN926⁃34；TP273

文献标识码：A

文章编号：1004⁃373X（2016）16⁃0010⁃04

doi：10.16652/j.issn.1004⁃373x.2016.16.003

作者简介：杨新伟（1982—），男，河南新乡人，讲师，硕士。主要从事电气自动化方面的教学与研究工作。郭彩霞（1979—），女，河南虞城人，讲师，硕士。主要研究方向为网络控制系统和鲁棒控制。

收稿日期：2015⁃12⁃25

基金项目：国家自然科学基金（61273120）；河南省教育厅科学技术研究重点项目（01026631079）

Stability design for networked control system with uncertain time delay

YANG Xinwei，GUO Caixia
（College of Physics and Electrical Engineering，Henan Normal University，Xinxiang 453007，China）

Abstract：Since the control systems have characteristics of network time⁃delay and uncertainty in the network environment，a common mode feedback controller without assigning specify parameters in advance is used to establish the closed⁃loop network control system model with the state feedback by taking into account of fact that the lower bound of the maximum allowable net⁃work induced delay is not zero and the system has uncertainty characteristics.The quadratic integral item in Lyapunov⁃Krsaso⁃vskii functional is defined directly by introducing the integral inequality approach，which can avoid the conservative property caused by model transformation of the system and definition of the cross terms.On this basis，the condition that makes the net⁃worked control system robust stability is derived.The state response curve of the system is obtained by conducting Matlab simulation for the model.The system state tends to be stable，which shows the validity and feasibility of the conclusion.

Keywords：network control system；network deduced time⁃delay；integral inequality approach；Lyapunov⁃krasovskii func⁃tion