基于变模式分解和频谱特性的自适应降噪算法

陆振宇，赵为汉，何珏杉，李　凯

（1.南京信息工程大学 电子与信息工程学院，江苏 南京　210044；2.江苏省大气环境与装备技术协同创新中心，江苏 南京　210044）

基于变模式分解和频谱特性的自适应降噪算法

陆振宇1，2，赵为汉1，何珏杉1，李凯1

（1.南京信息工程大学 电子与信息工程学院，江苏 南京210044；2.江苏省大气环境与装备技术协同创新中心，江苏 南京210044）

摘要：机械故障检测过程中，由于反映机械故障的振动信号微弱，很容易被外界噪声干扰信号污染，从而影响机械故障诊断。为提取纯净振动信号，传统EEMD滤波算法虽具有较强的降噪能力，但由于EEMD算法存在缺乏严谨理论基础、运算效率低、容易造成有用信号丢失等缺点，致使降噪效果不理想。为解决以上问题，提出一种基于变模式分解和频谱特性的自适应降噪算法。基于变模式分解优点，通过分析有用信号模态与噪声模态频谱特性，提取有用信号模态从而实现降噪。通过仿真信号与实测信号分析表明，新算法降噪效果优于传统EEMD滤波算法。

关键词：振动信号；降噪算法；变模式分解；频谱方差；轴承故障

0　引　言

机械故障诊断与状态监测依赖于对机械振动信号进行分析，然而采集的振动信号混有大量噪声干扰信号，其中噪声势必会影响对振动信号的分析，因此如何滤除噪声、提取纯净振动信号是故障诊断的基础。

传统滤波方法把信号映射到频域范围内，利用噪声信号与有用信号频率的差异性，设置合适的滤波器参数对噪声信号进行滤除［1］。然而由于噪声频率特性复杂，因此难以设计合适的滤波器滤除噪声，这就限制了滤波效果。小波阈值降噪效果虽优于传统滤波方法，但存在以下问题：小波降噪效果依赖于信号采样频率；难以选择合适的小波基和阈值函数［2］。Huang等人提出的EMD是一种新的时频分析算法［3］。该方法将原始信号分解成多个表征信号特征时间尺度的固有模态函数（IMF），具有良好的时频分析能力。但EMD算法缺乏严谨的理论基础，同时分解过程中容易出现端点效应、模态混叠等问题。黄锷等人针对EMD的缺陷，提出了集合经验模态分解（EEMD）算法［4］，利用高斯白噪声具有频率均匀分布的统计特性，将白噪声添加到原信号中，能够有效解决模态混叠现象。EEMD虽一定程度上降低EMD中模态混叠现象，但仍会带来新的模态混叠、丢失频谱、运算效率低等问题［5］。变模式分解（VMD）是一种新的信号分解方法［6］，通过对模态函数重新定义，假设各模态分量为具有不同中心频率的有限带宽，通过交替方向乘子法，不断迭代运算，将各模态解调到对应基带上，最终提取各个模态分量。VMD通过预设分解尺度，避免过度分解，运算效率较高，同时有效分离频率相近的分量，避免模态混叠现象，更适合信噪比低情况下的噪声处理。

因此本文基于VMD分解优点，提出一种基于变模式分解和频谱特性的自适应降噪算法（SA⁃VMD），通过验证分析，SA⁃VMD降噪效果优于EEMD滤波。

1　变模式分解原理

变模式分解（VMD）是一种新的，完全自适应分解方法。通过对经典维纳滤波、希尔伯特变换、频率混合的回顾与分析，提出原始信号由k个中心频率为ωk的k个模态分量组成。具体求解步骤如下［7］：

1.1建立目标函数

首先利用希尔伯特变换求解各个模态uk（t）的单边频谱；然后引入指数项不断调整各个模态估计的中心频率，将每个模态频谱转移到基带；最后带宽估计通过高斯平滑解调信号来实现即梯度的二范围的平方，所产生的约束变分问题如下：

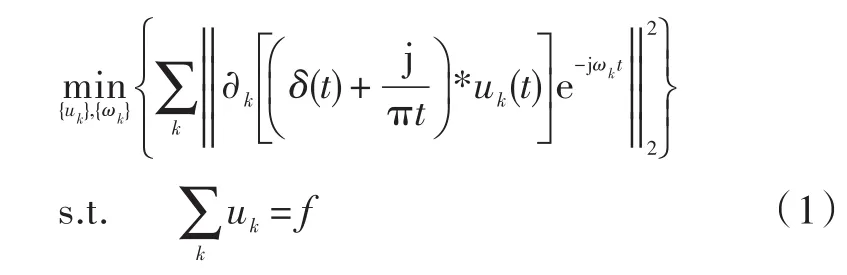
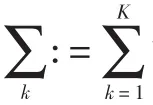
1.2求解目标函数

通过引入二次惩罚项和拉格朗日乘子将约束性目标函数转化为非约束性目标函数，其中二次惩罚项在有限罚权重下具有良好的收敛性，拉格朗日乘子使约束条件具有严格性，得到增广拉格朗日函数：

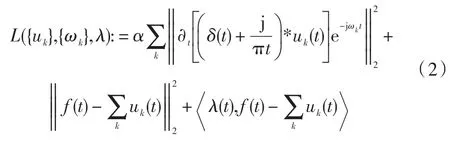
式中：λ（t）为拉格朗日乘子；α为数据保真约束的平衡参数。

利用交替方向乘子法（ADMM）将原先式（1）中的最小化问题转化为寻找增广拉格朗日表达式的“鞍点”问题。求解式（2）中的迭代问题如下：

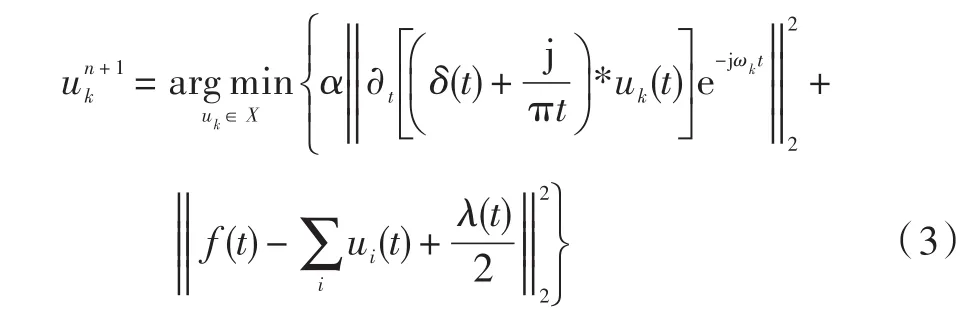
利用在梯度的二范数的平方下Paraseval/Plancher⁃el傅里叶变换等距，将式（3）转换到频域分析。

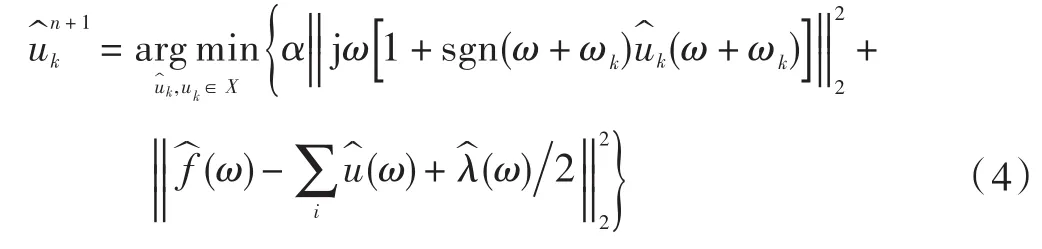
用ω-ωk替换式（4）第一项中ω：

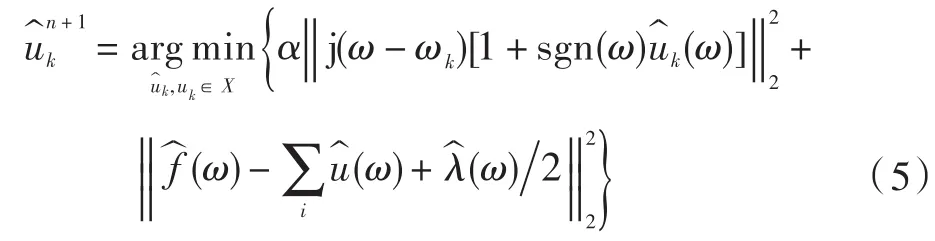
将式（5）转换为非负频率的半空间积分形式：

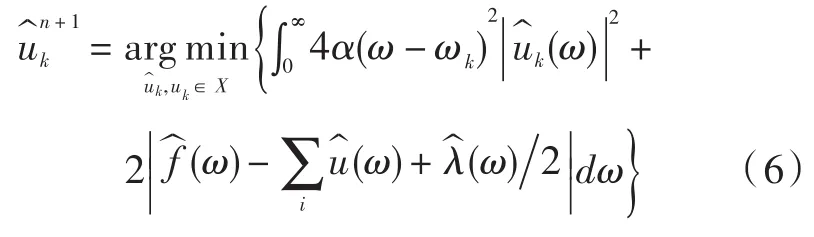
二次优化问题的解即：

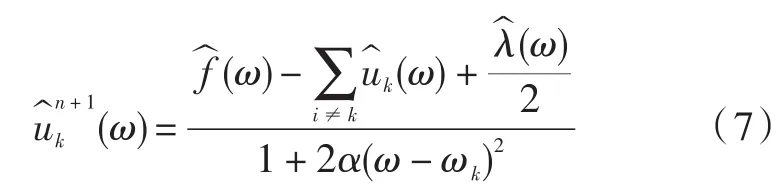
采用相同的求解过程将中心频率求解问题转换到频域：

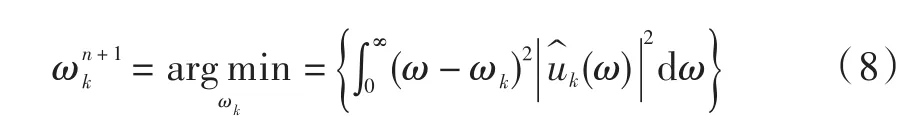
求得中心频率更新表达式：

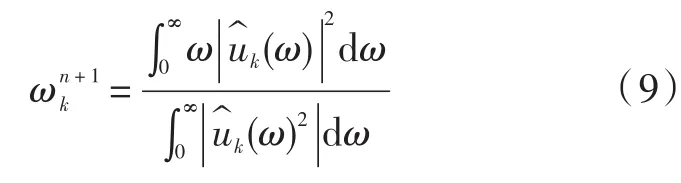
此表达式使新的ωk处于相应模态功率谱的重心。

总结完整的变模式分解算法步骤如下：

（2）n=n+1；

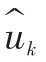
（5）对所有ω≥0，双上升步长：

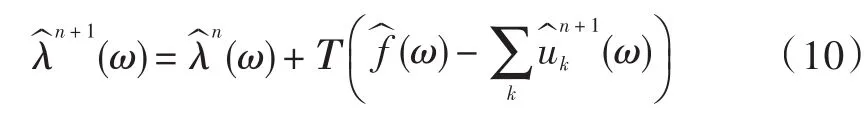
（6）满足判断收敛条件停止，否则回到步骤（2）：

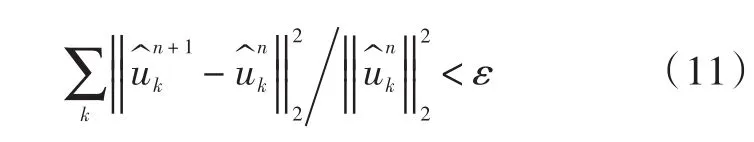
2　基于变模式分解和频谱特性的自适应降噪算法

传统EEMD滤波一般采用相关系数准则选择对应模态分量，但由于EEMD分解时易出现频谱丢失、模态混叠等现象，所以选择的模态分量可靠性较差，同时此方法在不同信噪比下降噪性能不稳定。本文针对传统EEMD滤波降噪算法缺点，提出利用变模式分解将原始信号分解成一系列模态分量，如何选择可靠性较高的有用信号模态分量，为此提出利用频谱方差方法。

2.1频谱特性

频谱分析是利用傅里叶变换将时域信号转换到频域信号进行分析。时域信号经傅里叶变换后变成若干单一的谐波分量以获得信号的频率结构以及各谐波和相位信息。若随机序列的自相关性越强，则频谱图中的谱线越集中，反之自相关性越弱，则谱线越分散［8］。

随机噪声信号，由于各时刻之间的弱关联性及随机性，所以反映在频谱图中谱线分散，频段分布较广。具有周期性的机械振动信号，信号之间存在着明显的关联性，所以谱线集中，频段分布较小。有用信号与噪声信号频谱对比见图1。

图1　有用信号与噪声信号频谱对比图

从图1中可以看出有用信号只在特定频段出现谱线幅值，而其他频率处幅值近似为零，幅值变化较大，因此频谱方差较大；噪声信号分布频带较宽且谱线幅值变化小，频谱方差较小［9］，其中计算频谱方差如式（12）、式（13）所示。

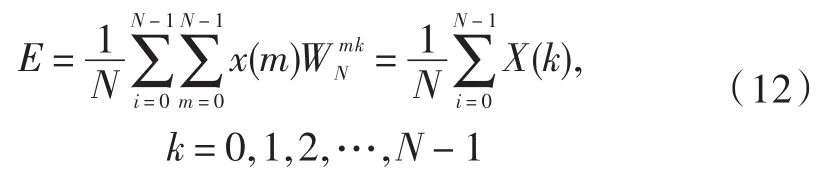
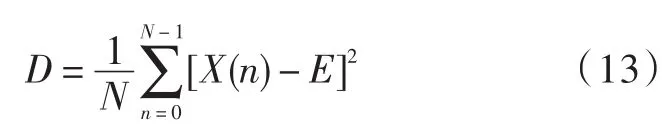
频谱方差体现振动信号能量变化程度，能量越大，幅值变化越剧烈，频谱方差越大［9］。按式（6）、式（7）分别计算噪声信号与有用信号频谱方差，分别为1.509 1×10-5和0.022 4，由此看出噪声信号频谱方差明显小于有用信号频谱方差。

2.2降噪步骤

基于VMD和频谱特性的自适应降噪算法具体步骤如下：

（1）对原始含噪信号采用自适应滤波器进行预处理，其中参考噪声为实测环境噪声或假设噪声。

（2）利用变模式分解（VMD）对预处理后信号进行分解，其中根据信号数据类型，设定分解模态数K。

（3）分别对各固有模式进行频谱分析，计算各固有模式频谱方差Dk，通过设定一个硬阈值λ来判定固有模式是否为有用信号。

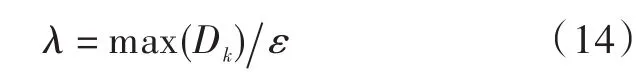
式中，max（Dk）为固有模式中最大频谱方差，k=1，2，…，K，ε设定为10。

（4）判断若Dk≥λ则判定为有用信号，否则为噪声信号或虚假信号。

（5）最后重构有用信号即可实现降噪。

3　验证分析

3.1仿真信号

假设原始信号为：

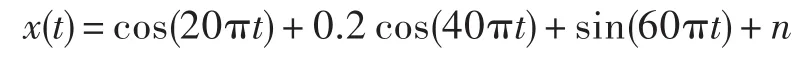
式中，n为高斯白噪声，取数据点2 000。其中有用信号被噪声干扰信号严重污染，无法识别，原始信号如图2所示。

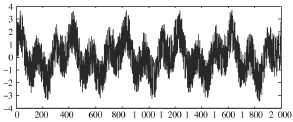
图2　原始信号

对原始信号进行VMD，其中10 Hz，30 Hz信号被完好地分离出来，20 Hz信号幅值较小，被噪声污染严重，分解结果较差，但经过VMD分解后，20 Hz中心频率被调整到此谐波上，VDM分解图如图3所示。根据EEMD的分解信号原理可知，EEMD将含噪信号分解成特征尺度由小到大，频率由高到低的IMF分量，其中阶数低的IMF分量一般为噪声信号，阶数高的IMF分量一般为有用信号。使用EEMD对原始信号处理，其中前四个IMF分量为噪声信号或高频有用信号，IMF5～IMF7最接近有用信号，但信号波形失真严重，出现模态混叠现象，这样不利于对信号进一步处理，同时由于EEMD分解的自适应性，受噪声影响较大，容易出现过分解现象，降低运算效率，其中EEMD分解如图4所示。

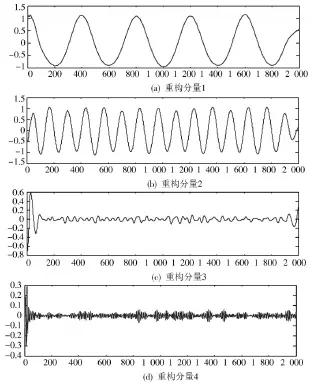
图3　VMD分解结果

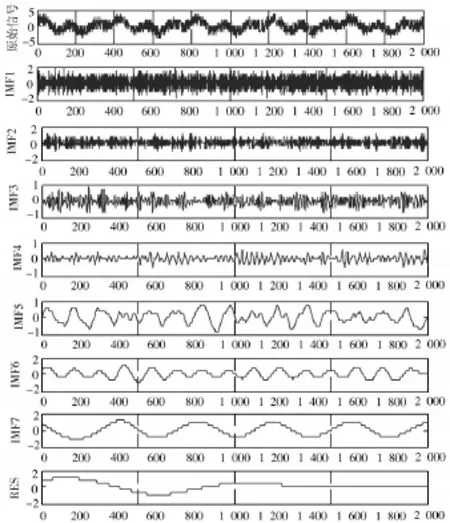
图4　EEMD分解结果

分别采用EEMD滤波与SA⁃EEMD对原始含噪信号进行处理，其中图5为两种算法降噪后波形，图6为两种算法降噪后频谱图。

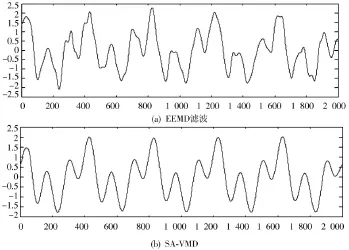
图5　两种算法滤波后效果图

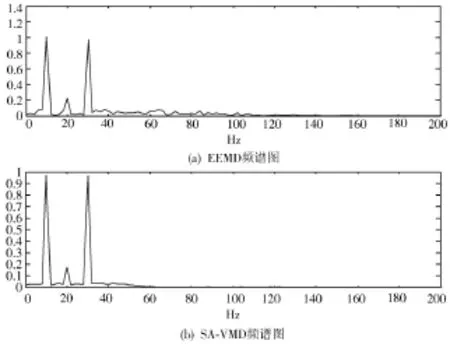
图6　两种算法滤波后频谱图

从图5中可以看出图5（a）EEMD滤波波形恢复效果较差，其中在数据点300，700，1 350处波形严重失真，这样不利于后期对信号的进一步分析。相反图5（b）SA⁃VMD算法波形得到良好恢复，波形光滑，降噪效果明显优于EEMD滤波。为了定量分析两种算法的降噪性能，本文通过计算信噪比、相关系数以及运行时间来验证本文算法的优越性见表1，其中相关系数与信噪比定义分别如式（15）、式（16）所示。

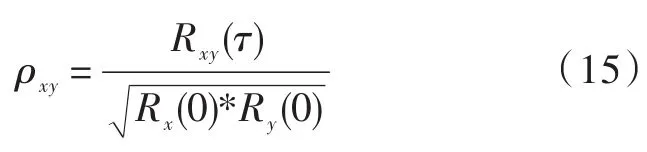
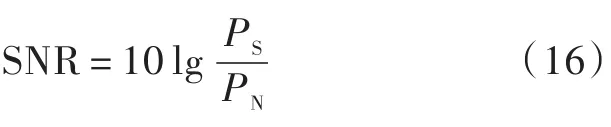
式中：PS为有用信号功率；PN为噪声功率。

从表1中可以看出EEMD降噪算法虽然信噪比提高约14 dB，但相关系数为0.981 2，损失部分有用信号。SA⁃VMD降噪算法信噪比大约提高18 dB，与原始信号相关系数为0.995 4，可以看出SA⁃VMD不仅具有良好的降噪能力，信号失真度小，而且SA⁃VMD运算效率明显高于EEMD，利于实时性分析。

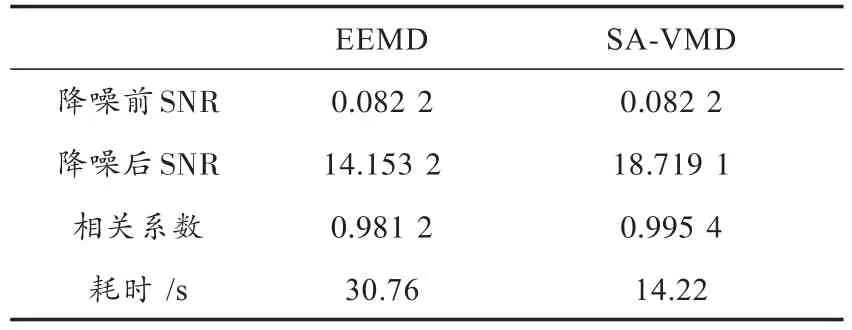
表1　EEMD与SA⁃VMD降噪性能比较

3.2实测信号

实验平台主要由电机、转轴、转速控制系统、传感器、数据采集卡等组成。可通过改变转速、轴承的磨损、油膜涡动来模拟机械运转。选用型号6205⁃2RS转轴，设定转速1 750 r/min，运行过程中人为加入噪声信号，同时制造轴承故障，使其产生故障信号，采集2 000点数据。含噪故障信号时域图与频谱图如图7所示，从图7中可以看出，有效信号主要集中在100 Hz以下，由于噪声信号的影响，微弱的转轴故障信号被淹没，无法得知转轴故障情况。

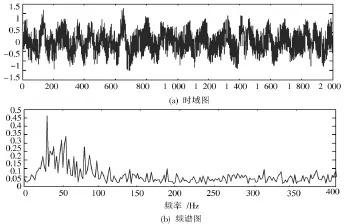
图7　原始故障信号

分别使用EEMD滤波和SA⁃VMD对信号进行处理，其中图8为EEMD降噪效果图，从图8中看出部分低频微弱信号丢失，波形恢复较差。图9为SA⁃VMD降噪效果图，降噪效果明显优于传统EMD降噪，波形达到良好恢复，充分保留原始信号特征。

表2为两种算法的降噪对比，从表2中可看出两种算法都实现降噪，提高信噪比，但EEMD来滤波在降噪的同时丢失了部分有用信号，其中相关系数为0.916 7。本文SA⁃EEMD算法降噪后信噪比达到18.560 9，相关系数为0.993 1，说明本文算法降噪效果明显优于EEMD滤波，波形恢复良好。同时从运行时间看出，SA⁃VMD运算效率高于EEMD滤波。综合以上性能比较，充分说明本文SA⁃VMD算法的可行性与高效性。

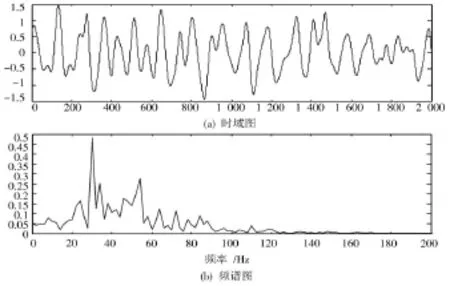
图8　EEMD降噪效果图

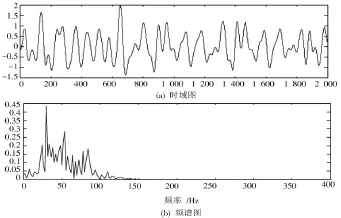
图9　SA⁃VMD降噪效果图

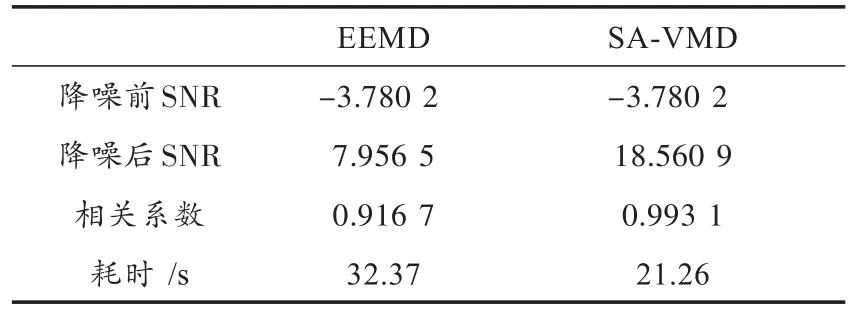
表2　两种算法降噪对比

4　结　论

本文提出一种基于变模式分解和频谱特性的自适应降噪算法（SA⁃VMD），首先对预处理后信号进行VMD分解，利用噪声模态与有用信号模态频谱的差异性，提出通过计算频谱方差，设定方差阈值，从而重构有用信号模态以达到降噪目的。通过仿真实验表明，SA⁃VMD具有良好的模态识别能力，降噪效果良好。相比于传统EEMD滤波，SA⁃VMD通过预设分解尺度，避免信号过度分解，抗模态混叠能力强，运算效率高，利于实时分析。同时SA⁃VMD在消除噪声干扰，保留有用信号特征，自适应性等方面优势明显。

参考文献

［1］赵志宏，杨绍普，申永军.一种改进的EMD降噪算法［J］.振动与冲击，2009，28（12）：35⁃37.

［2］陈仁祥，汤宝平，吕中亮.基于相关系数的EEMD转子振动信号降噪方法［J］.振动、测试与诊断，2012，32（4）：542⁃546.

［3］HUANG N E，SHEN Z，LONG S R，et al.The empirical mode decomposition and the Hilbert spectrum for nolinear and no⁃stationary time series analysis［J］.Proc R Soc London A，1998，454：903⁃995.

［4］WU Z H，HUANG N E.Ensemble mode decomposition：a noise assisted data analysis method［J］.Advances in adaptive data analysis，2008，1（1）：1⁃41.

［5］曲建岭，王小飞，高峰，等.基于复数据经验模态分解的噪声辅助信号分解方法［J］.物理学报，2014（11）：1⁃9.

［6］DRAGOMIRETSKIY K，ZOSSO D.Variational mode decompo⁃ sition［J］.IEEE transactions on signal processing，2014，3 （62）：531⁃544.

［7］刘江，吕勇.基于变模式分解降噪的滚动轴承故障诊断研究［J］.机械设计与制造，2015（10）：21⁃25.

［8］刘新飞，周辉.基于谱减法及频谱方差的语音端点检测方法［J］.兵工自动化，2014（4）：34⁃38.

［9］刘玉珍，连自锋.基于频谱方差的抗噪声语音端点检测算法［J］.计算机仿真，2010，27（9）：337⁃340.

［10］肖倩，王建辉，方晓柯，等.一种基于互相关函数的小波系数相关阈值去噪算法［J］.东北大学学报（自然科学版），2011，32 （3）：318⁃321.

中图分类号：TN911⁃34

文献标识码：A

文章编号：1004⁃373X（2016）16⁃0001⁃05

doi：10.16652/j.issn.1004⁃373x.2016.16.001

作者简介：陆振宇（1976—），男，江苏常州人，副教授，硕士研究生导师，博士。主要研究方向为模式识别、智能控制。赵为汉（1990—），男，江苏宿迁人，硕士研究生。主要研究方向为振动信号处理。何珏杉（1989—），男，河南商丘人，硕士研究生。主要研究方向为信号处理与智能控制。李凯（1990—），男，江苏徐州人，硕士研究生。主要研究方向为信号采集与处理。

收稿日期：2015⁃12⁃08

基金项目：国家自然科学基金（61473334；61104062）

Adaptive denoising algorithm based on variable mode decomposition and spectrum characteristics

LU Zhenyu1，2，ZHAO Weihan1，HE Jueshan1，LI Kai1
（1.School of Electronic&Information Engineering，Nanjing University of Information Science and Technology，Nanjing 210044，China；2.Jiangsu Collaborative Innovation Center on Atmospheric Environment and Equipment，Nanjing 210044，China）

Abstract：In the process of mechanical fault detection，the vibration signal reflecting the fault feature is weak and is easy to contaminate by outside noise，which increases the difficulty of diagnosing the mechanical fault.In order to extract the pure vi⁃bration signal and solve the above problem，an adaptive denoising algorithm based on variable mode decomposition and spec⁃trum characteristics is proposed，because the traditional ensemble empirical mode decomposition（EEMD）filtering algorithm lacks rigorous theoretical foundation，has low operation efficiency and is easy to make the useful signal lost，which may cause a poor denoising effect although it has strong ability of denoising.On the basis of the advantages of variable mode decomposition，the useful signal mode is extracted to achieve denoising by means of analyzing the spectrum characteristics of useful signal mode and noise mode.The analysis results of the simulation signal and the measured signal show that the new algorithm is superior to the tradition EEMD in denoising.

Keywords：vibration signal；denoising algorithm；variable mode decomposition；spectrum variance；bearing fault