ARIMA模型与指数平滑法对山东省GDP的实证分析

郭新颖（兰州财经大学统计学院，甘肃兰州730020）

ARIMA模型与指数平滑法对山东省GDP的实证分析

郭新颖
（兰州财经大学统计学院，甘肃兰州730020）

文借助Eviews6.0和Excel软件，建立了ARIMA（1，2，1）预测模型和三次指数平滑预测模型，对山东省1978年到2010年国内生产总值（GDP）数据进行分析，并对2011年到2013年的GDP进行预测。结果表明，ARIMA模型预测结果与真实值相比平均相对误差小，结果更为精确，基本符合事实。因此，选择ARIMA（1，2，1）模型作为最优模型为有关部门制定经济发展战略、经济发展规划提供重要依据。

经济统计；ARIMA模型；指数平滑法；GDP预测

改革开放以来，随着工业化、城市化和国际化进程的不断加快，山东省经济飞速发展。2013年，全省GDP实现54684.3亿元，比上年增长9.6%，人均生产总值56323元，增长9.0%，被评为中国最具综合竞争力的省区之一。本文选取山东省进行研究，从侧面反映我国国民经济的未来走势，为政府制定经济发展战略提供依据。图1为山东省1978年到2010年GDP数据变化时序图。

图1　山东省1978年到2010年GDP时序图

1　ARIMA模型预测法

从图1可以看出，山东省1978年到2010年GDP呈现出明显的趋势性，在1978年到2000年缓慢增长，之后又呈现出强劲的增长趋势。因此考虑该序列为非平稳时间序列。用Eviews6.0，进行ADF单位根检验精确判断其平稳性，检验结果见表1。

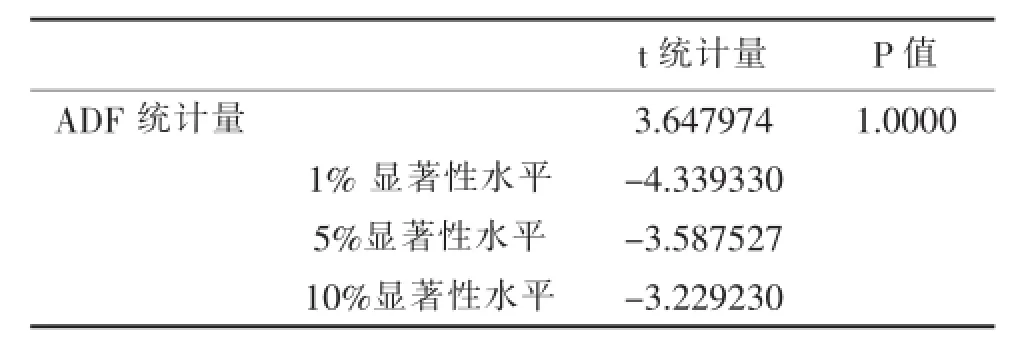
表1　GDP序列的ADF检验结果

从结果看，t=3.647974，分别大于显著性水平为10%、5%和1%的临界值，因此不能拒绝该序列存在单位根原假设，该序列可能存在单位根，不满足平稳条件，需要对序列进行差分。经测算，二阶差分后的序列基本平稳。所以，ARIMA（p，d，q）模型中的d=2，确认该模型为二阶单整序列。

我们尝试拟合ARIMA（1，2，1）、ARIMA（1，2，2）、ARIMA（2，2，1）、ARIMA（2，2，2）模型，最终根据AIC准则评价模型优劣，确定最优模型。表2为拟合结果。

表2　各模型AIC值大小

结果显示，ARIMA（1，2，1）模型的AIC值最小，对ARIMA（1，2，1）进行回归，结果见表3。

表3中，各参数的p值为0，均小于0.05，参数估计有效。因此，二阶差分后GDP序列的ARIMA（1，2，1）模型 为 ：Δ2GDPt=34.63281-1.361730Δ2GDPt-1+εt-1.66847εt-1。R2=0.75，精度较高，可以用来做短期预测。

表3　回归结果

对ARIMA（1，2，1）模型的残差序列进行白噪声检验模型有效性，结果如图2所示。

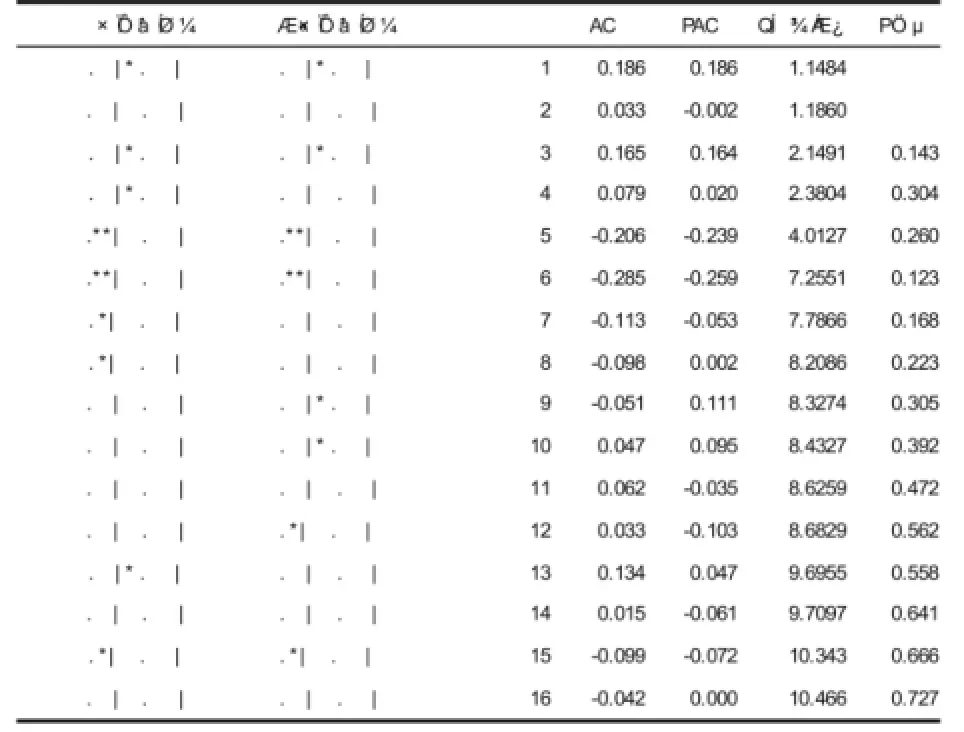
图2　ARIMA（1，2，1）残差序列白噪声检验图

检验结果显示，自相关图都落在两倍标准差之内，并且P值都大于0.05，因此可以95%的置信水平接受原假设，认为该残差序列为白噪声序列，模型通过检验，可用来预测。

利用ARIMA（1，2，1）模型，对山东省2011年到2013年GDP进行预测，其预测值与真实值比较结果见表4。

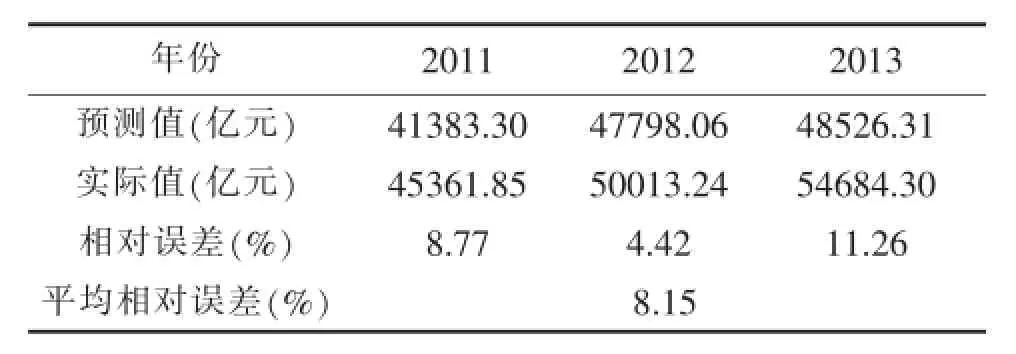
表4　ARIMA（1，2，1）模型的预测值与真实值得比较数据表

2　指数平滑预测法

由图1，1978年到2010年GDP序列呈现出二次曲线的增长趋势，因此，利用Excel对该数据进行三次指数平滑预测。经测算，当a=0.1时，MSE3= 4537.87；当a=0.6时，MSE3=9962.07；当a=0.9时，MSE3=21785.73。

根据MSE最小原则，选择a=0.1为平滑系数。由此得出at=32766.15，bt=2353.11，bt=34.19，预测模型为：=32766.15+2353.11T+34.19T2，t=2010。预测结果见表5：

表5　指数平滑法的预测值与真实值得比较数据表

3　结论

运用指数平滑法与ARIMA模型对山东省2011年到2013年GDP进行预测，得出两种预测结果的平均相对误差分别为 24.64%与 8.15%。所以，ARIMA（1，2，1）模型预测结果的平均相对误差比指数平滑法小，效果较好，因此选择ARIMA（1，2，1）模型为最优预测模型。

比较两种预测方法，都没有考虑影响因素的种类和个数，只考虑了数据的过去值、现在值和误差值，利用数据本身的信息对未来进行预测。指数平滑预测法有原理简单，操作简便，易于解释，但只能把过去存在的发展趋势继续运用在将来，对随机性信息浪费严重。而ARIMA模型预测法在预测的过程中既考虑了经济现象在时间上的依存性，又考虑了随机波动的干扰性，虽然过程较为繁琐，但得到了更加理想的预测结果。在实际的GDP预测中，也许不能把所有因素都考虑周全，因此，可以采用ARIMA模型为主，指数平滑法为辅的方式，综合分析预测出最优的结果。

［1］赵玉新.多元线性回归分析中自变量的筛选［J］.经济观察，2011（11）：32-34.

［2］丁文斌.GDP总量预测方法探讨研究［J］.统计与预测，2003（5）：57-59.

［3］孙彩，姜明辉.基于GP的非线性GDP预测模型的构建与应用［N］.哈尔滨工业大学学报，2008（1）：133-138.

［4］G.P.E.BOXandG.MJenkins.TimeSeriesAnalysis：Forcastingandcontrol［M］.SanFrancisco：SanFrancisco Press，1978.23-25.

［5］王燕.应用时间序列与分析［M］.第2版.北京：中国人民大学出版社，2008.44.

F201