裂隙膨胀土边坡稳定性分析方法研究*

王晓磊，　田　存，　黄丽丽，　范冀哲

(1.河北工程大学 土木工程学院，河北 邯郸 056038；2.河北工程大学 信息与电气工程学院，河北 邯郸 056038)



裂隙膨胀土边坡稳定性分析方法研究*

王晓磊1*，田存1，黄丽丽2，范冀哲1

(1.河北工程大学 土木工程学院，河北 邯郸 056038；2.河北工程大学 信息与电气工程学院，河北 邯郸 056038)

基于反映裂隙影响的膨胀土边坡稳定性的极限平衡法，提出了通过将边坡划分为裂隙充分发展区A、坡顶张拉裂隙区A′、裂隙发育不充分区B、坡顶张拉裂隙区B′、坡脚雨水积聚影响区C以及无裂隙区D，近似反映坡顶张拉裂隙以及坡脚渗流积聚对边坡稳定性的影响.研究确定了C、B′区域的强度指标取值，尝试对该极限平衡方法进行完善补充.利用毕肖普法进行实例计算，结果表明：单独考虑坡脚雨水积聚和坡顶张拉裂隙影响时边坡安全系数分别下降0.271和0.082，同时考虑两者影响时降幅达9%.提出的方法能够反映膨胀土滑坡的特点，同时可以计算裂缝发展极限状态时边坡的稳定状态.

裂隙；膨胀土；降雨；稳定性； 极限平衡法

膨胀土因其剧烈的胀缩性、裂隙性和超固结性等特点，使其赋存区域的边坡工程建设面临诸多的问题与巨大的挑战.例如，南水北调中线工程穿越386.8 km 的膨胀土区域，滑坡隐患治理给水渠建设造成巨大的资金投入[1、2].对膨胀土边坡的稳定性分析，国内外各类规范首选的方法就是极限平衡方法.但是传统的极限平衡方法在计算过程中忽略了膨胀土边坡裂隙和降雨入渗的影响，计算结果不符合膨胀土滑坡的实际情况.当前对于极限平衡分析法的研究主要侧重于三维边坡稳定性分析的实现以及最小安全系数的临界滑面搜索[3～9].对于极限平衡方法计算边坡稳定性时考虑裂隙和降雨影响的研究尚不多见.

林鲁生等[10]运用非饱和土强度理论,提出非饱和土等效凝聚力新概念，使用Bishop法等极限平衡法考虑雨水入渗影响的边坡稳定分析计算.但是需要获得不同降雨时刻土中含水量状态，确定土体的抗剪强度.在实际操作中实现困难，使此方法的应用受到限制.殷宗泽等[11]通过将膨胀土边坡划分成裂隙充分发展层、裂隙发育不充分层和无裂隙层3个亚层，以极限平衡方法为基础，取用不同的强度指标，近似反映裂隙影响的膨胀土边坡稳定性分析方法.但是提出方法未对以下三方面进行深入的研究：(1)坡顶存在张拉裂隙；(2)坡脚第一层内渗流积聚对下部第二亚层的影响；(3)各亚层深度的研究.

本文首先对坡顶张拉裂隙和坡脚雨水积聚对边坡的影响进行了分析研究，然后在文献[11]的成果基础上，通过改变极限平衡方法的计算条件对上述问题进行考虑，尝试对其进行补充和完善，建立更符合实际的考虑裂隙、降雨影响的传统极限稳定性分析方法，使该极限平衡方法对于膨胀土边坡的分析具有更广泛的适应性，为膨胀土边坡的设计与加固提供理论依据.

1　坡顶张拉裂隙及坡脚雨水积聚对边坡的影响分析

1.1张拉裂隙对边坡稳定性的影响

实际状态中的膨胀土边坡在自身重力、雨水入渗等各种作用下，坡顶往往存在深度较大的张拉裂隙，滑坡发生时成为滑坡体的后壁.张拉裂隙的存在对边坡的稳定性产生了很不利的作用.

(1) 裂隙使边坡开放，降雨直接进入边坡内部.膨胀土边坡表层土体风化严重，裂隙纵横发育，张拉裂隙中降雨积水在边坡内部迅速入渗，影响区域内土体软化，抗剪强度急剧下降，接近残余强度.

(2) 降雨过程中坡顶张拉裂隙内部积水，产生静水压力和渗流力.积水对边坡产生向临空侧的推力作用(如图1所示).这些不利作用随着裂隙深度的增加而增大，加剧边坡的不稳定性.

1.2坡脚雨水积聚对下部亚层土体的影响

降雨过程中，裂隙土体中发生雨水渗流，从微观上形成了一个沿着裂隙底部顺斜坡方向向下的“微细孔道”，最后在坡脚处积聚.文献[12]现场含水量测定结果可以证实这一现象.

随着坡脚处积聚雨水的不断入渗，下部土体含水量上升，土体浸水软化，抗剪能力急剧下降.抗剪强度指标相比于边坡上部土体同一土层要有所下降.积聚雨水影响范围越大，愈大范围的土体抗剪强度下降，边坡稳定性越差.因而在计算当中应该考虑坡脚渗流聚集对下部土体的影响.参照文献[11]，将浸润线假定为水平直线，位置在1/3坡高处.如图2所示.

2　计算方法

2.1张拉裂隙对边坡稳定性的影响

本文的计算方法采取能够考虑水平作用力的传统极限平衡分析方法，如毕肖普法和简布法等.在计算过程中能够计算裂隙积水对潜在滑体的推力作用.

2.2区域的划分

本文针对膨胀土边坡实际工作状态，对边坡坡顶存在张拉裂隙、降雨过程中坡脚渗流积聚的情况进行了考虑.另外，还研究了各亚层深度的取值.

(1) 边坡区域的划分

参照文献[11]反映裂隙膨胀土边坡稳定性的方法，按照裂隙的发育程度将土体分成裂隙充分发展层、裂隙发育不充分层和无裂隙层.

本文考虑降雨过程中，裂隙充分发展层雨水渗流在坡脚处土体积聚以及坡顶张拉裂隙对边坡稳定性的影响，对边坡进行了细分：(1)将裂隙充分发展层划分为裂隙充分发展区A、坡顶张拉裂隙区A′；(2)将裂隙发育不充分层细分为裂隙发育不充分区域B、坡脚雨水积聚影响区C和坡顶张拉裂隙区B′三个分区；(3)无裂隙区D.划分后边坡区域分布如图3所示.

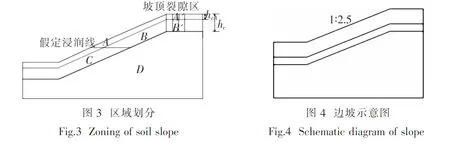
(2) 分层深度确定

① 裂隙充分发展层A深度hcA的确定

文献[13]利用线弹性力学理论得出裂隙扩展深度的弹性力学解.其求解公式为

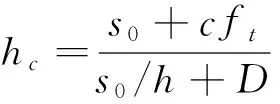
(1)

本文在考虑降雨过程的影响时，假定膨胀土裂隙充分发展层A土体吸水饱和，此时基质吸力s0=0.将s0=0代入式(1)可以得到本文划分的裂隙充分发展层A深度的计算公式.

hcA=cft/D,

(2)

式中：s0为边坡膨胀土地表基质吸力；c=(1-μ)/(1-2μ)；D=μγ/(1-2μ)；ft为膨胀土的抗拉强度.

② 裂隙发育不充分层深度hc的确定

边坡裂隙在气候因素影响下发育深度不断变化，因而边坡的稳定性也是动态的.因此当前状态下裂缝的深度可以反映当前状态下边坡的稳定性.裂隙发展到极限状态时，反映边坡最终的安全程度.

裂缝深度即裂隙发育不充分层深度可以通过现场试验方法，如含水量随深度的变化，地温随深度的变化，锥尖阻力随深度的变化等方法间接获得.姚海林等[13]曾通过含水量和现场静力触探试验得出裂隙影响深度同上述两个指标近似一致的结论，此时得到的裂隙深度反映的是当前状态下边坡的状态，用于当前状态下边坡稳定性的评价.

有些长期工作的边坡不但要保证边坡当前安全，而且在整个服务期限内都要确保其稳定，比如南水北调工程的渠道边坡以及水库边坡等.这就需要确定边坡裂缝的极限深度.文献[13]裂缝扩展深度的极值

hcmax=(s0+cft)/D

(3)

用于边坡永久性稳定性评价.

上述确定裂隙发育不充分层的深度hc可以计算当前状态下边坡的稳定状况，又可以根据裂隙发展极值计算边坡永久安全系数.

2.3不同区域强度指标的确定

裂隙充分发展层A为强风化层，徐彬等[14]通过试验分析表明：裂隙充分发展的膨胀土强度指标接近残余强度，故可用其作为裂隙充分发展层的强度指标cr和φr.D区土体位于大气影响深度以下，取原状土的饱和固结不排水强度c0和φo.B区处于裂缝区向原始土体过渡区域，土体强度近似认为介于两者之间，其强度指标取A区和D区强度指标的平均值,即

(4)

其余各分区强度指标本文取值具体如下：

C区土体由于受到坡脚雨水积聚的影响，含水量大于同层上部B区土体，导致强度下降，其抗剪强度指标取B区和A区强度指标平均值，即

(5)

A′和B′为张拉区，当张拉裂隙深度未达B′区域时，B′土体抗剪强度指标取B区值.当张拉裂隙深度达到B′区域时，B′土体抗剪强度指标取A区值,即

(6)

式中h为坡顶张拉裂隙深度.

2.4裂隙积水和渗流力的考虑

当边坡存在深大裂隙时，强降雨条件下充满积水,压力水头对边坡产生向临空侧的推力作用.压力值按式(7)计算.

p=γh,

(7)

式中，γ为水的重度，h为张拉裂隙的深度.

渗透力的影响参考文献[11]的方法采用替代重度法计算.浸润线以下的裂隙区，饱和重度计算滑动力矩，浮重度计算抗滑力矩.

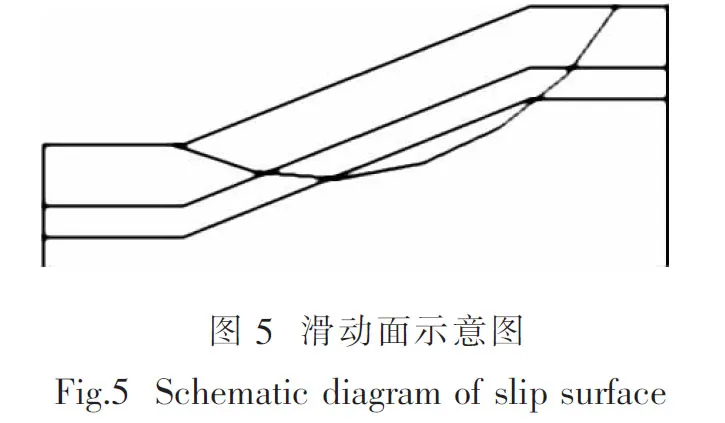
2.5滑动面

本文滑动面位置参考文献[11]中的局部滑动面，便于本文考虑坡顶张拉裂隙等因素的计算结果与其进行对比分析.

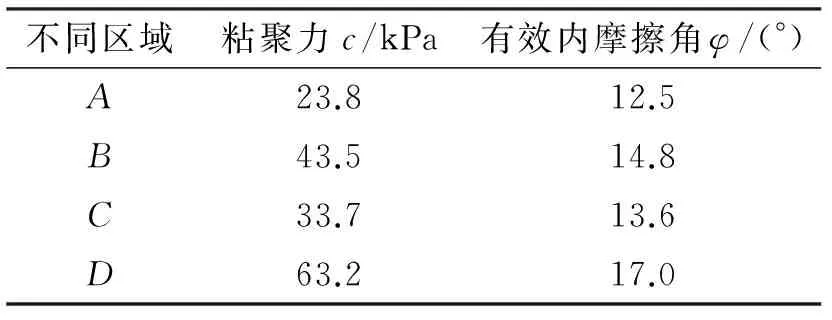
表1　抗剪强度指标Tab.1　Parameters of shear strength

3　实例分析

3.1工程实例

工程分析实例采用图4所示的边坡计算模型.由式(4)～(6)计算采用的土体强度指标见表1.

3.2计算工况

计算工况首先参照文献[11]取值深度，并采用本文考虑坡脚雨水积聚和坡顶张拉裂隙影响的方法对边坡稳定性进行计算；然后采用本文方法确定各亚层深度及其区域划分计算边坡稳定性；最后将各工况条件下计算结果进行对比分析.

工况详细如下：工况①——各亚层深度按文献[11]取值，按本文方法考虑坡脚雨水积聚影响；工况②——各亚层深度按文献[11]取值，按本文方法考虑坡顶张拉裂隙影响；工况③——各亚层深度按文献[11]取值，按本文方法考虑坡脚雨水积聚和坡顶张拉裂隙影响，为使计算结果更加具有对比性，计算过程中人为控制各个工况的滑动面，使得工况①～工况③的滑动面均与文献[11]中的滑动面一致；工况④——按照本文方法计算边坡永久稳定性.本例中基质吸力和抗拉强度取自文献[2]中新乡地区膨胀土平均值，s0=45 kPa，抗拉强度ft=15 kPa.根据式(1)和式(3)得出工况④裂隙充分发展层hcA=1.9 m，裂隙发育不充分层极限值hcmax=5 m.坡顶张拉裂隙深度为2 m，超过完全风化层A深度.各工况计算结果见表2.

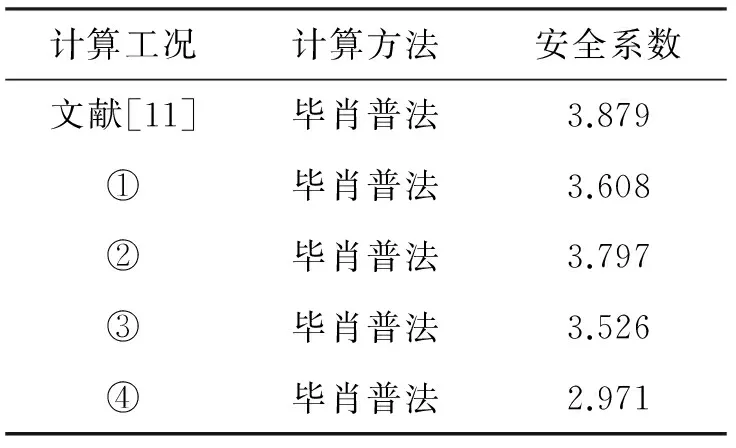
表2　边坡稳定性计算结果Tab.2　Numerical results for slope stability

3.3结果分析

(1) 坡顶张拉裂隙是边坡的一种实际存在状态.当降雨过程中张拉裂隙充满积水时，积水产生的静水压力会对边坡产生向临空侧的推力作用，从而由工况②得出的安全系数相对于文献[11]中不存在坡顶张拉裂隙时要有所降低，但安全系数降幅较小，本例中同一滑动面下降了0.082.

(2) 单独考虑降雨过程中坡脚雨水积聚对下部土体的影响时，计算得出的安全系数为3.608，相比于文献[11]的计算结果，安全系数下降了0.271.相对于单独考虑坡顶裂缝的影响来说，边坡的安全系数对坡脚雨水积聚具有较高的敏感性.

(3) 由工况③的计算结果可知：同时考虑坡顶张拉裂隙和坡脚雨水积聚影响时，安全系数为3.526，其降幅达近9%.因而膨胀土边坡的稳定性分析中不可忽略上述两种不利因素的作用.

(4) 将工况④的计算结果与文献[11]所提出方法的计算结果进行对比，工况④的安全系数由3.879降为2.971，下降了23%，安全系数下降.原因是文献[11]假定裂隙发育不充分层深度为裂隙深度hc的2/3，即2.66 m.此安全系数即为边坡裂缝开裂极限状态时，降雨条件下边坡的局部安全系数.

(5) 依本文所述，坡顶张拉裂隙和坡脚雨水集聚会对边坡的稳定性带来不利的影响，但是所带来的影响的大小视边坡不同的工作状态而定，关键在于边坡的潜在滑动面是否通过坡顶张拉裂隙区以及坡脚雨水积聚区.

4　结　论

在文献[11]的基础上，通过对坡顶存在张拉裂隙和降雨过程中坡脚雨水积聚影响的考虑，尝试对其方法进行补充和完善.计算结果表明：坡体张拉裂隙和坡脚雨水积聚在边坡稳定性分析中必须给予考虑.方法既继承了文献[11]反映膨胀土滑坡的平缓性、浅层性、季节性、方向性等特点，又能反映坡顶张拉裂隙影响以及对降雨过程中坡脚雨水积聚的情况.使极限平衡方法的适用性更加广泛.

本文方法旨在将文献[11]极限平衡方法进行补充和完善，使其更好满足膨胀土边坡实际状况.其中浸润线位置以及强度过渡层的指标取值均为近似假定，由于现场实际资料有限，期待在以后工程实践中进一步验证.

[1]陈浩元,郑进保,李兴昌.科技书刊标准化18讲[M].北京:北京师范大学出版社，2000.

[2]廉玲军,王韦,徐威,等.洞塞泄洪洞的三维数值模拟研究[J].四川大学学报:工程科学版,2011,43(3):1-6.

[3]刘特洪.工程建设中的膨胀土问题[M].北京:中国建筑工业出版社,1997.

[4]张均锋，丁桦．边坡稳定分析的三维极限平衡法及应用[J] .岩石力学与工程学报,2005,24(3):365-370.

[5]张均锋．三维简化Janbu法分析边坡稳定性的扩展[J].岩石力学与工程学报,2004,23 (17):2 876-2 881.

[6]李亮，迟世春，林皋．基于粒子群优化的复合形法求解复杂土坡最小安全系数[J].岩土力学,2005, 26(9):1 393-1 398.

[7]王成华，夏绪勇，李广信．基于应力场的土坡临界滑动面的遗传算法搜索[J].清华大学学报(自然科学版),2004,44 (3) :425-428.

[8]陈云敏，魏新江，李育超．边坡非圆弧临界滑动面的粒子群优化算法[J].岩石力学与工程学报，2006，25(7):1 443-1 449.

[9]李亮，迟世春，林皋．禁忌鱼群算法及其在边坡稳定分析中的应用[J].工程力学，2006，23(3):6-10.

[10]林鲁生,蒋刚．考虑降雨入渗影响的边坡稳定分析方法探讨[J].武汉大学学报(工学版),2001,34(1):42-44.

[11]殷宗泽,徐彬．反映裂隙影响的膨胀土边坡稳定性分析[J].岩土工程学报,2011,33(3):454-459.

[12]NG C W W， ZHAN L T，BAO C G，et al. Performance of an unsaturated expansive soil slope subjected to artificial rainfall infiltration[J].Géotechnique，2003 ，53(2)：143-157.

[13]姚海林，郑少河，葛修润．裂隙膨胀土边坡稳定性评价[J].岩石力学与工程学报,2002,21(增2):2 331-2 335.

[14]徐彬，殷宗泽，刘述丽．膨胀土强度影响因素与规律的试验研究[J].岩土力学,2011,32(1):44-50.

责任编辑：罗联

Study of Stability Analysis Method for Expansive Soil with Fissures

WANGXiao-lei1*,TIANCun1,HUANGLi-li2,FANJi-zhe1

(1.College of Civil Engineering,Hebei University of Engineering, Handan 056038；2.College of Information & Electrical Engineering, Hebei University of Engineering, Handan 056038 China)

A new method was proposed based on the slope stability analysis of expansive soil under fissure influence, by dividing the slope into fully fissures areaA,top slope tension crack influence areaA′,the partially developed fissures areaB, top slope tension crack influence areaB′, toe of slope rainwater accumulation influence areaC, and no fissures areaD, to reflect the influences of tension fissures and rainwater accumulation on slope stability approximately. And the strength indexes were determined for areasCandB′from this research, trying to improve the limit equilibrium method and make it for perfect complement. The computed results using bishop method of an example showed that when the influence of rainwater accumulation and tension crack considered separately the safety coefficient of slope dropped respectively 0.271 and 0.082, and the amplitude reduction was 9% when consider them together. The proposed method can not only reflect the characteristics of expansive soil landslide but also calculate the slope stability for fissures at ultimate state.

fissures; expansive soil; rainfall; stability; limit equilibrium method

2015-10-08

国家自然科学基金项目(51274126)；河北省教育厅项目(QN2014070)

王晓磊(1983-)，男，河北 石家庄人，博士，讲师. E-mail:wangsanshi2003@163.com

TU43

A

1000-5900(2016)01-0027-06