聚能装药作用下夹层玻璃的破坏研究

张少华，苟瑞君



聚能装药作用下夹层玻璃的破坏研究

张少华，苟瑞君

（中北大学化工与环境学院，山西 太原，030051）

ANSYS LS-DYNA仿真模拟软件，采用Lagrange和ALE流固耦合方法对夹层玻璃进行了数值仿真研究。玻璃材料采用JH-2模型，并施加最大主应力失效准则。结果表明：不同冲击能量作用下夹层玻璃失效破坏和四周裂纹扩展存在着一定的规律，玻璃失效破坏的长度、速度、加速度等参数随着冲击能量增加呈现增长趋势；在裂纹扩展方面，冲击能量不同时玻璃的裂纹起裂时刻与内能减少时刻基本相同，裂纹产生条数和裂纹密度都随着冲击能量的增加而增大。

聚能装药；冲击能量；失效破坏；裂纹扩展

近年来随着人们对安全的重视和科技的快速发展，夹层玻璃在多数车型上得到越来越多的应用[1]。然而进入21世纪以来，公交车、大巴等各类汽车的劫持事件频繁发生。一旦恐怖分子进入车内劫持人质，公交和大巴车就成了最好的掩体，给解救工作带来极大的困难，因此，采用聚能装药技术研制玻璃爆炸切割装置或警用破窗器已成必然。

目前首要工作是对聚能装药作用下夹层玻璃的破坏过程进行研究。国内外学者对不同种类的夹层玻璃进行了大量的实验和仿真模拟研究。在试验方面，陈晶晶等[2]利用落锤实验结合高速摄影装置对PVB夹层玻璃板进行面外冲击试验，并进行了相关的数据分析研究，得出了玻璃裂纹扩展与PVB薄膜厚度和冲击能量的关系。刘博涵等[3]开展了一系列的头模块与夹层风挡玻璃在不同冲击速度、冲击角度下的参数化冲击试验，结果为风挡玻璃的吸能特性研究提供了必要的试验和理论基础。陶志雄等[4]通过PVB薄膜剪切试验，得出了PVB的应力应变关系式并给出了常温和高温下的剪切模量值，研究结果为建立夹层玻璃的力学模型提供了重要的试验依据。在仿真模拟方面，Xujun等[5]采用传统的有限元法对低速冲击下夹层玻璃的损伤裂变和失效行为进行了初步的研究。李胜杰等[6]利用裂纹扩展的方法对结构在爆炸载荷下的动态响应进行了数值仿真，定性地分析了不同爆炸距离和不同TNT当量作用下夹层玻璃的裂纹扩展情况。江祺等[7]借助ANSYS/LS-DYNA程序较好地反映了玻璃的冲切破坏现象。高伟、雷周、臧孟炎等[8]采用离散元/有限元耦合方法，针对汽车夹层玻璃的冲击破坏问题进行了系统的分析研究，较好地模拟了材料的破坏、裂纹的产生及传播，真实地反映了脆性材料的破坏及能量释放。

总结来看，现阶段关于夹层玻璃的分析研究主要集中于低速和头部模块冲击，而关于聚能装药作用下的相关研究较少。因此，本研究借助ANSYS/LS- DYNA程序，在线型切割器产生的聚能射流基础上，通过对玻璃材料施加主应力失效准则，初步探讨和分析了夹层玻璃在聚能装药作用下的破坏和裂纹扩展规律，为警用破窗器的设计提供了相应的指导。

1 材料方程和参数的选取

1.1 线型切割器的材料选择

本研究中线型切割器是产生聚能射流的构件，其中外壳和药型罩采用T2紫铜材料，它具有加工性能良好、物理化学性能优异等特点；炸药采用装药密度小的黑索今，容易起爆且综合性较好[9]。

1.2 夹层玻璃的材料选择

夹层玻璃由外层玻璃、PVB薄膜和内层玻璃3部分组成。外层玻璃和内层玻璃选用专门针对脆性材料开发出来的LS-DYNA中的110号材料*MAT_ JOHNSON_HOLMQUIST_CERAMICS模型（简称JH-2)，为模拟出玻璃在破坏后的破碎现象，对两层玻璃材料施加主应力失效准则，应力大小为84MPa。其主要的力学参数为：弹性模量E=72GPa，泊松比ν=0.22，密度ρ=2 530 kg•m-3。

作为中间夹层的PVB薄膜是一种半透明的薄膜，它是由聚乙烯醇缩丁醛树脂经增塑剂塑化挤压成型的一种高分子材料。PVB薄膜是一种线性粘弹性材料体，在模拟中采用*MAT_VISCOELASTIC模型（LS- DYNA中6号材料）。其主要的力学参数为：弹性模量E=0.1GPa，泊松比ν=0.49，密度ρ=1 100kg•m3，瞬态剪切模量0=0.33GPa，永久剪切模量∞= 0.69MPa。

1.3 参数选择与结构设计

外层玻璃和内层玻璃的材料参数如表1所示，PVB薄膜的材料参数如表2所示。整体结构示意图见图1。

表1 玻璃的材料参数(cm、g、μs）

Tab.1 Material parameters of glass

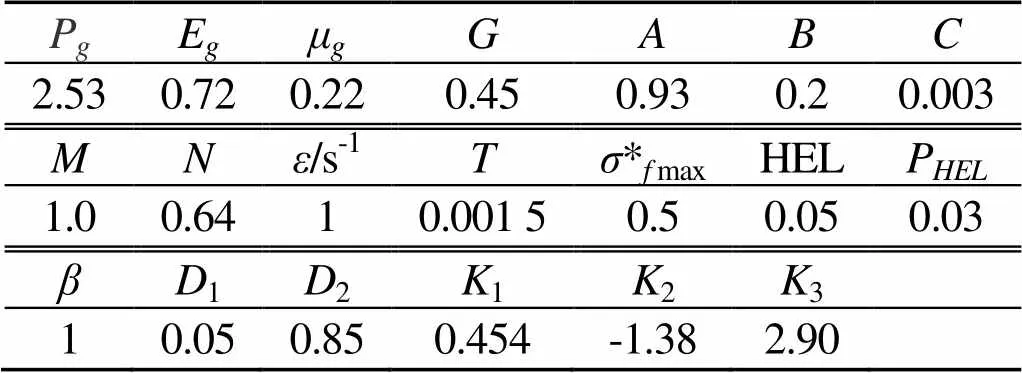
PgEgμgGABC 2.530.720.220.450.930.20.003 MNε/s-1Tσ*f maxHELPHEL 1.00.6410.001 50.50.050.03 βD1D2K1K2K3 10.050.850.454-1.382.90

表2 PVB的材料参数(cm、g、μs)

Tab.2 Material parameters of PVB

PkG0G∞B 1.10.23.3E-36.9E-70.0

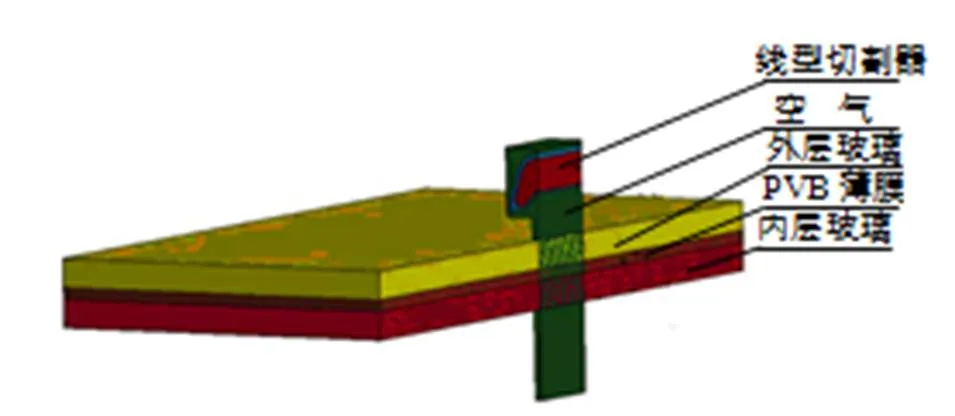
图1 玻璃模型整体结构示意图

2 算法及有限元模型

线型切割器和空气部分算法参照文献[10]。其中先在线型切割器和空气的一面进行自由网格划分，然后对体进行扫略网格划分。根据线型切割器的实际大小划定每个网格的尺寸最小为0.1mm。对夹层玻璃整体采用六面体映射网格划分，每个网格的尺寸0.3mm；两层玻璃和PVB薄膜之间的接触算法采用带有失效模式的*CONTACT_TIED_SURFACE_TO_SUR FACE _ FAILURE算法，以描述玻璃与PVB薄膜之间的粘结性。模型整体构件具有对称性，因此为提高运算效率减少计算，采用1/2三维结构建模，在对称面上施加对称约束，在夹层玻璃的其他3个面上施加全约束以进行玻璃简支方式模拟，并在此基础上施加透射边界以消除应力波传播过程中在边界的反射影响。整个结构中线型切割器和空气采用欧拉网格建模和多物质ALE算法，夹层玻璃试件采用拉格朗日网格建模，通过流固耦合算法将两者连接起来。有限元模型如图2所示。

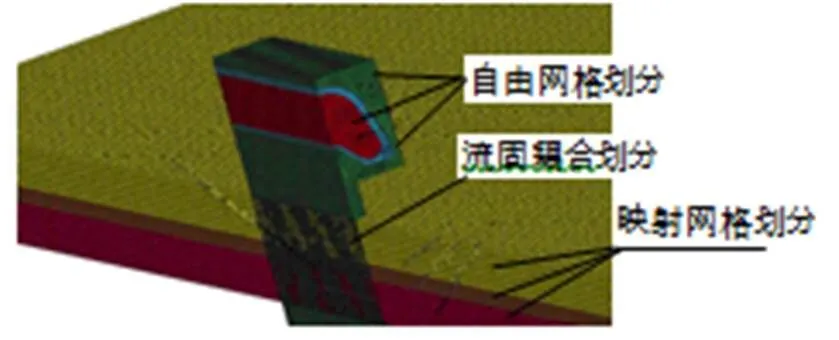
图2 有限元模型图

3 数值模拟过程及分析

3.1 数值模拟模型选择

参照文献[10]中的研究成果选择4种不同结构的线型切割器，其射流头部最大速度分别可以达到2 520.15m/s、2 628.19 m/s、2 809.53 m/s、3 021.78m/s，产生的射流部分所能达到的最大动能分别为3.80 kJ、4.45 kJ、4.80 kJ、5.25kJ，分别记录对应型号为A、B、C、D。对夹层玻璃试件，选择汽车夹层玻璃中比较常见的厚度搭配，即2mm+0.76mm+2mm（外层玻璃+PVB薄膜+内层玻璃）作为模拟研究的对象。同时在模拟过程中考虑模型的简化原则，在进行建模时进行两点简化处理：（1）夹层玻璃边界固定方式进行简化处理，对边界实行全约束，进行简支方式模拟；（2）以平板夹层玻璃为研究对象，暂不考虑具有一定弧度的汽车前风挡玻璃等夹层玻璃。

3.2 不同冲击能量下玻璃失效破坏过程分析

3.2.1 玻璃失效过程展示

玻璃材料是典型的脆性材料，其抗拉强度/抗压强度比值极低，破坏模式一般为拉伸破坏。线型切割器产生的聚能射流先作用到外层玻璃（受冲击面玻璃），其高速冲击作用使得外层玻璃在1.5μs之内被贯穿失效，随后冲击波通过PVB薄膜到达内层玻璃表面反射形成拉伸波，拉伸波导致内层玻璃大面积失效破坏。因此本研究工作首先以内层玻璃为研究对象，对冲击作用下玻璃表面的破坏过程进行分析。在LSPP后处理中，通过将失效单元重新显示可以清晰地观察到玻璃的失效破坏区域变化。

失效破坏的整个过程如图3所示（线型切割器为B型）。参照文献[2]中的裂纹捕捉方法，分别定义玻璃表面失效的两个参数：长（）和宽（），玻璃失效破坏的长度=（+)/2。以4μs为基准单位，记录100μs失效破坏过程中的25组数据，并采用B样条插值法对记录的数据进行平滑处理。

3.2.2 数据记录及分析

将不同冲击能量作用下玻璃材料的失效破坏长度——时间曲线进行对比分析，如图4所示。

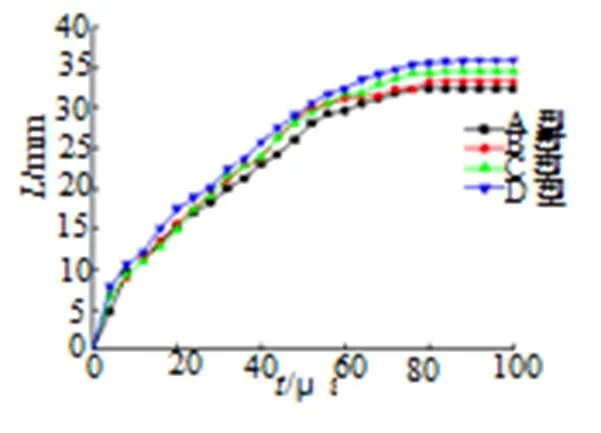
图4 不同冲击能量作用下玻璃失效破坏长度——时间曲线

由图4可知不同型号的线型切割器（即不同冲击能量）下，玻璃材料的破坏过程有如下几个特点：（1）冲击能量越大，玻璃最后失效破坏长度相对越长；（2）整个过程基本可以分为玻璃失效破坏长度加速增加、平稳增加和趋近于零3个阶段；（3）玻璃中间区域失效破坏过程基本在70~100μs之间结束，并随着冲击能量增加结束时间随之延后。对长度——时间曲线进行求导可得到玻璃失效破坏的速度——时间曲线，如图5~6所示。

由图5~6速度曲线可知：（1）整个冲击过程速度——时间曲线可分为3个阶段：速度上升阶段（0~24μs之间），速度下降阶段（24~70μs之间），冲击过程结束阶段（70~100μs之间）；（2）冲击能量越大，速度上升阶段持续时间越长，且所能达到的速度峰值越大；（3）速度下降阶段存在着第2峰值，当冲击能量越大，速度第2峰值越大；（4）由冲击过程结束阶段（70~100μs之间）放大图可知，冲击能量越大，玻璃失效破坏速度减小到0的时刻越晚，整个破坏过程持续时间越长。总的来说，随着冲击能量的增加，整个曲线越陡峭，所能达到的速度峰值越高，且玻璃破坏过程持续时间越长。

将不同冲击能量作用下玻璃失效破坏的加速度——时间曲线进行对比，如图7所示。分析可知：（1）玻璃失效破坏的加速度在起始时刻为最大值，整个过程中加速度先由最大值迅速减小到负值，而后在0值左右进行震荡过程，最后趋近于0。（2）随着冲击能量的增加，玻璃破坏起始时刻加速度值最大；（3）随着冲击能量的增加，加速度变化曲线越陡峭，所达到的峰值越小。即整个过程中随着冲击能量的增大，加速度变化趋势越明显，玻璃失效破坏过程越剧烈。

3.3 不同冲击能量下玻璃裂纹的产生及分析

仍以内层玻璃为研究对象，记录不同冲击能量作用下100μs时玻璃表面的破坏及裂纹扩展情况，如图8所示。从图8中分析可以得出以下结论：（1）随着冲击能量的增大，玻璃中心失效破坏区域和周围裂纹条数都随之增加。（2）裂纹先于玻璃试件四周区域产生，而后与玻璃中心失效破坏区域迅速连接，并随着冲击能量的增大玻璃裂纹产生密度也随之增大。

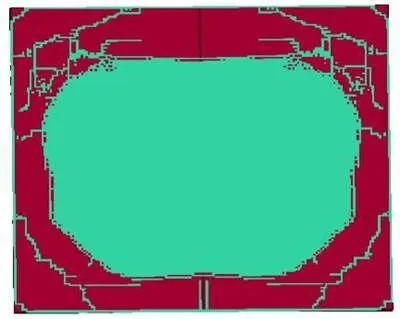
(a) D型 (b) C型

(c) B型 (d) A型

图8 玻璃在不同冲击能量作用下的裂纹特征

Fig.8 Crack characteristics of glass under the action of different impact energy

记录不同冲击能量下玻璃四周裂纹起裂时刻1，裂纹持续时间2、裂纹密度大小、内层玻璃总体内能最大值1、内能开始减小时间3、最终结束时内能大小2、1与2之差3。具体数值及对比见表3。从能量角度进行分析，首先引入能量释放率。从定义来看，能量释放率是裂纹扩展单位面积时裂纹体所释放出来的弹性能；从量纲来看，能量释放率是裂纹扩展一个单位长度时所需要的力，也就是企图驱动裂纹扩展的原动力，所以又称裂纹扩展力。由于能量释放率是从能量分析出发得到的概念，因而具有普遍适用的优点[11]。

由文献[10]可知，文中所用线型切割器所产生的射流在10~15μs之间某时刻动能可忽略不计，所以整个冲击过程大致可分为15μs之前的外载荷施加和15μs之后夹层玻璃自身的能量驱动。在外载荷施加阶段，外力所做功一部分用于增加结构的应变能，另一部分用于推动玻璃中心区域的失效破坏，因此在20μs之前玻璃中心区域的失效破坏速度呈上升趋势，之前所做的模拟也验证了这一点。在夹层玻璃自身能量驱动阶段，起始时刻玻璃结构的应变能储存较多，可以推动玻璃中心区域进一步失效破坏，同时速度也大大降低。

表3 不同冲击能量下玻璃裂纹的相关参数

Tab.3 Relevant parameters of glass crack under the different impact energy

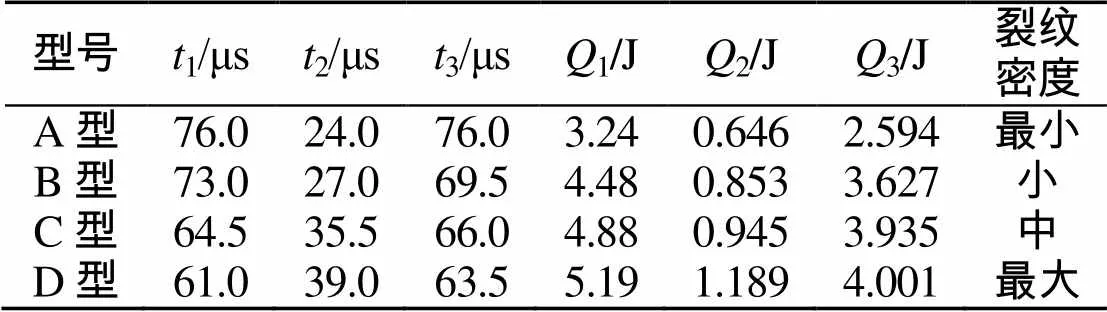
型号t1/μst2/μst3/μsQ1/JQ2/JQ3/J裂纹密度 A型76.024.076.03.240.6462.594最小 B型73.027.069.54.480.8533.627小 C型64.535.566.04.880.9453.935中 D型61.039.063.55.191.1894.001最大

分析表3中的数据可知，玻璃试件内能开始减小时刻3与裂纹起裂时刻1基本相等，这表明玻璃自身所得到的应变能开始推动裂纹扩展。当冲击能量越大时，玻璃本身得到的应变能越多，推动裂纹扩展耗散的能量也越多，最终产生的裂纹密度也随之增大。

4 结论

采用数值模拟方法对聚能装药作用下夹层玻璃的破坏过程进行了研究，对比分析了不同冲击能量作用下夹层玻璃中心区域失效破坏的长度、速度、加速度等参数，在此基础上对夹层玻璃周围的裂纹扩展进行了初步的探讨分析。研究表明，玻璃中心区域的破坏和周围的裂纹扩展过程都与冲击能量有着显著的关系，随着冲击能量的增加，夹层玻璃中心失效区域显著增大，其本身的应变能提高并随后推动玻璃周围区域的裂纹扩展速度加快，最终裂纹条数和密度都随着冲击能量的增加而增大。研究结果得到了必要的基础数据和分析，为爆炸切割装置及警用破窗器的设计提供了一定的理论基础。

[1] 孟欣,王娜,白云峰.浅谈汽车玻璃发展趋势[J].玻璃, 2015 (1): 39-43．

[2] 陈晶晶,许俊,刘博涵,等. PVB夹层玻璃裂纹扩展的参数化实验研究[J].汽车工程,2015,37(2): 235-240．

[3] 刘博涵,王岩,徐晓庆,等.头模块低速冲击下PVB夹层风挡玻璃的吸能特性试验研究[J].机械工程学报,2013,49(22): 128-136．

[4] 陶志雄,张其林,陈俊,等.夹层玻璃PVB胶片抗剪性能试验研究[J].结构工程师, 2011, 27(1):134-138．

[5] Xu Jun,Li Yi-Bing,Chen Xi,et al. Characteristics of windshield cracking upon low-speed impact: numerical simulation based on the extended finite element method[J]. Computational Materials Science, 2010, 48(3):582-588.

[6] 李胜杰,李志强,王志华,等.爆炸载荷作用下夹层玻璃裂纹扩展的研究[J].兵工学报, 2014, 35(s2):72-77.

[7] 江祺,刘彤,王汝恒,等.爆炸冲击波对3种建筑玻璃的作用过程[J].爆炸与冲击, 2014, 34(2):229-234.

[8] 高伟.汽车玻璃冲击破坏现象的离散元/有限元耦合仿真方法研究[D].广州:华南理工大学,2013.

[9] 杜学良,苟瑞君,候红宵,等.线型聚能切割器切割靶板过程相似率的数值模拟[J].工程爆破,2012,18(2):18-21.

[10] 杜学良.铜管线型聚能切割器的数值模拟研究[D].太原:中北大学,2012.

[11] 郦正能,关志东,张纪奎,等.应用断裂力学[M].北京:北京航空航天大学出版社, 2012.

Study on Destruction of Laminated Glass under the Impact of Shaped Charge

ZHANG Shao-hua，GOU Rui-jun

( School of Chemical Engineering and Environment, North University of China，Taiyuan，030051)

To explore the destruction effect of laminated glass under shaped charge, the fluid-structure interaction methods of Lagrange and ALE were introduced to numerical simulation on laminated glass, through ANSYS/LS-DYNA software. JH-2 model was adopted, and maximum principal stress failure criterion was exerted for the glass material. Results showed that a certain rule was existed between laminated glass failure destruction and crack growth under the action of different impact energy. That is, with the increase of impact energy, the length, velocity and acceleration of glass failure destruction presented a growth trend. Additionally, in terms of crack growth, the moment when the crack of glass initiated and its internal energy decreased was synchronous under various impact energy. And the article number and density were also increased with the increase of impact energy.

Shaped charge；Impact energy；Failure destruction；Crack growth

TJ410.3+4

A

[12]2016-03-30

张少华（1990 -），男，硕士研究生，从事聚能装药应用技术研究。