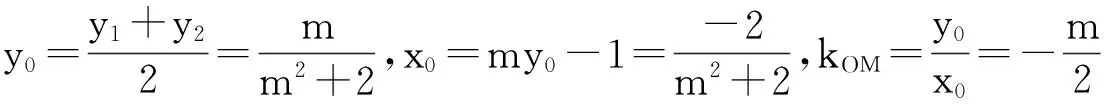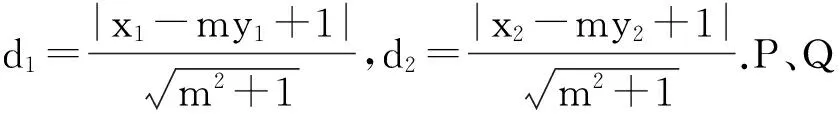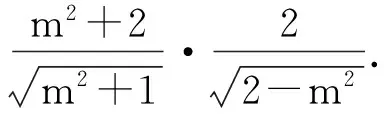圆锥曲线中四边形的面积

云南省曲靖市第一中学　(655000)

张国坤



圆锥曲线中四边形的面积

云南省曲靖市第一中学(655000)

张国坤

如图1，四边形MPNQ的四个顶点在圆锥曲线C上， 已知圆锥曲线及四边形两条对角线的方程，如何求(表达)四边形MPNQ的面积？

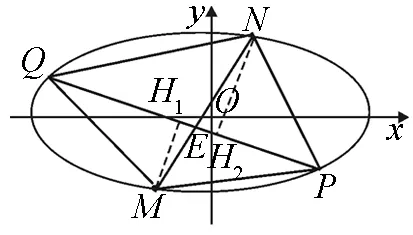
图1

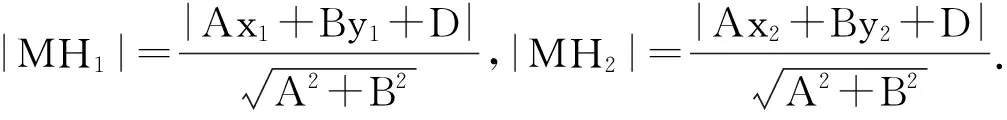
(1)M、N位于PQ两侧，则代数式Ax1+By1+D与Ax2+By2+D异号，|MH1|+|NH2|

(x1=x2时，k不存在，特殊处理)

(2)M、N位于PQ同侧时，代数式Ax1+By1+D与Ax2+By2+D同号，||MH1|-|MH2||

方案三：PQ的方程为Ax+By+D=0，则(B,-A)是PQ的一个方向向量，(A,B)是与PQ垂直的一个向量(法向量)．

(1)求M的方程；

(2)C、D为M上的两点,若四边形ABCD的对角线CD⊥AB,求四边形ADBC面积的最大值．

图2

解：根据题意作出示意图形如图2．

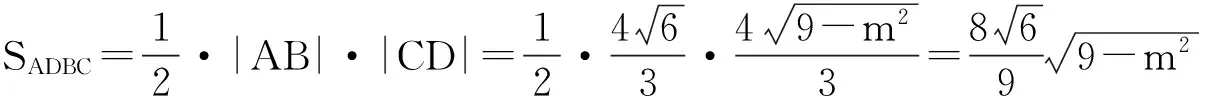
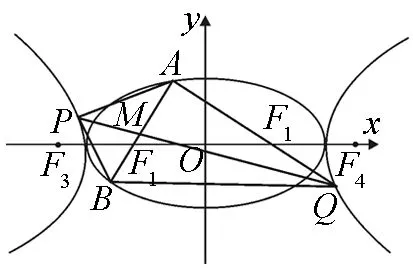
图3

(1)求C1,C2的方程；

(2)过F1点作C1的不垂直于y轴的弦AB,M为AB的中点,当直线OM与C2交于P,Q两点时,求四边形APBQ面积的最小值.