基于时间函数的并联六维力传感器量程设计*

刘琬钰, 王志军, 田雪珂, 崔建国, 李占贤

(华北理工大学 机械工程学院，河北 唐山 063009)



基于时间函数的并联六维力传感器量程设计*

刘琬钰, 王志军, 田雪珂, 崔建国, 李占贤

(华北理工大学 机械工程学院，河北 唐山 063009)

针对并联六维力传感器设计与制造过程中面临的解耦计算复杂、量程确定困难、实用性不强等问题，应用螺旋理论，推导了其受六维外力向测量分支反作用力的映射矩阵；基于工程实际，提出并建立了并联六维力传感器测量分支作用反力的时间函数模型；提出了一种在特定工作环境下测量分支量程的确定方法。以Stewart并联结构为例，针对曲面打磨作业，确定了其测量分支的量程，验证了时间函数模型的正确性和可行性。研究内容对提高并联结构六维力传感器的工程应用性有重要的实践价值。

六维力传感器; 测量分支; 时间函数; 量程

0　引　言

六维力传感器由于能够检测空间力/力矩信息而在机器人、航空航天等高新技术领域有着迫切的需求[1～3]。

并联结构在六维力传感器设计中广为应用[4,5]。并联六维力传感器测量分支的优化设计是提高其实用性的重要途径。各向同性是目前普遍认可的优化准则[2，6]。当传感器结构满足该准则时获得的平均信息量最大[7]，但这并不能说明传感器满足某特定工作下的测量要求。为使传感器满足各方向上的测量需求，王航等人提出了任务模型[8]。但任务模型会受某些结构的限制，其设定的任务条件可能影响结构稳定性，使优化过程不易实现。由于六维力传感器的解耦计算困难[9]，很难根据任务模型确定测量分支量程，这也给其实际应用带来困难。因此，提出一种简单可靠的测量分支设计方法，使得六维力传感器能够满足不同作业需求，是高新技术产业智能化进程中急需解决的问题。

本文推导了并联六维力传感器在工作时受到六维外力影响向测量分支作用反力的映射矩阵；结合工况，提出了时间函数模型的概念，建立了针对特定任务的测量分支反作用力时间函数模型；提出了一种可通用的并联六维力传感器测量分支量程设计方法；最后，以Stewart结构为例，针对机器人曲面打磨作业进行了测量分支量程设计。研究内容为提高六维力传感器的实用性奠定了基础。

1　传感器静力学平衡方程

图1为并联六维力传感器结构示意图。在测力平台上建立基坐标系O-xyz，其上的测量分支球铰点在基坐标系中的位置用矢量b1,b2,…,bn表示，固定平台上的测量分支球铰点在基坐标系中的位置用矢量B1,B2,…,Bn表示。

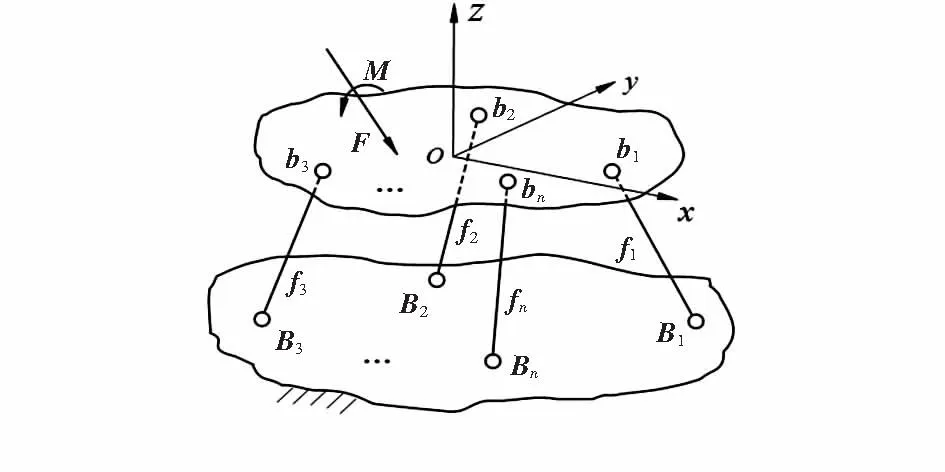
图1　并联六维力传感器结构示意图Fig 1　Structure diagram of parallel six-axis force sensor

建立测力平台的静力学平衡方程为

Fw=Gfn

(1)

式中Fw为作用在测力平台上的六维外力矢量，Fw=[FxFyFzMxMyMz]T；fn为由测量分支轴向力组成的向量，fn=[f1f2…fn]T；G为测量分支轴向力到空间六维外力的映射矩阵，维数为6×n；根据螺旋理论，将G表示为[10]

(2)

将fn看做未知数，在传感器结构非奇异，即G的列向量不相关时，静力平衡方程有解。此时若n=6，则静力平衡方程有唯一解；若n>6，静力平衡方程有无穷多解，此时引入伪逆矩阵进行求解。伪逆矩阵具有唯一性[11]，它保证了方程有唯一解。

2　传感器外力映射矩阵

六维外力作用在传感器的测力平台上时，若测量分支数n=6，则G为方阵，此时有伪逆矩阵G+=G-1，在式(1)两边同时乘以G+得

f6=G+Fw

(3)

若n>6，静力学平衡方程有无穷多组解，则

fn=G+Fw+(I-G+G)y

(4)

式中I为 n×n维单位矩阵；y为n维任意列向量，即y=[y1y2… yn]T。

式(4)中得到的测量分支轴向力包含两部分，分别由方程组的特解和通解组成，将其表示为

fR=G+Fw

(5)

fP=(I-G+G)y

(6)

式中特解fR为外力作用下的测量分支反作用力；通解fP为初始内力。由式(5)、(6)可得出结论:初始力fP仅与结构参数有关，在结构参数一定的情况下，分支反作用力fR受六维外力Fw影响。

由式(3)、式(5)可以看出，在测量分支数 时，作用在测力平台上的六维外力向测量分支轴向力的传递关系完全由G+决定。设仅由六维外力产生的测量分支轴向力为fw，有

Fw=G+Fw

(7)

式中fw为n维向量，表示为fw=[f1w…fnw]T。称G+为六维外力向测量分支反作用力的映射矩阵，它只与传感器结构参数有关。

3　时间函数模型

对机器人需测量的关节进行力学分析，可知其在工作过程中理论上所受的六维外力变化情况。将Fw表示为在工作周期T内变化的函数Fw(t)为

Fw(t)=[Fx(t)Fy(t)Fz(t)Mx(t)My(t)

Mz(t)]T

(8)

结合工程实际，易知Fw(t)中各项应在T内均有定义且均为有界函数。

将式(8)带入式(7)，则测量分支反作用力的函数表达式fw(t)为

fw(t)=G+Fw(t)=[f1w(t) …fnw(t)]T

(9)

式中fiw(t)(i=1,2,…,n)为Fw(t)中各项的代数和，则fiw(t)也在工作周期T内有定义且均为有界函数，即在定义域I=[0,T]内，存在ti0∈I和ti1∈I使得对于任意t∈I都有

fiw(ti0)≥fiw(t)≥fiw(ti1)i=1,2,…,n

(10)

设fiw(t)的最大值fiw max=fiw(ti0)，最小值fiw min=fiw(ti1)。由此，第i个测量分支在工作周期T内的作用反力fiw的范围为[fiw min,fiw max]。通常测量分支量程应为对称区间，且受力数值应尽量靠近量程中部。设Mi为满足机器人正常工作时测力需求的第i个测量分支的计算量程。

当fiw min≥0时，取

Mi=[fil,fir]=[fiw min-2fiw max,2fiw max-fiw min]

(11)

当fiw max≤0时，取

习近平主席近日在亚太经合组织工商领导人峰会发表主旨演讲指出，40年来，中国人民依靠自身的智慧和勤劳的双手，在风雨中砥砺前行，迎来了从站起来、富起来到强起来的历史飞跃，开启了中华民族伟大复兴的光辉历程。40年来中国人民勇于探索、真抓实干、凭着一股开拓创新的拼劲，一股自力更生的韧劲，把中国建成了世界第二大经济体，中国的面貌、中国人民的面貌发生了翻天覆地的变化。中国的今天是中国人民干出来的。

Mi=[fil,fir]=[2fiw min-fiw max,fiw max-2fiw min]

(12)

当fiw max≥0且fiw min≤0时，取

Mi=[fil,fir]=[fiw min-fiw max,fiw max-fiw min]

(13)

式(11)～式(13)中，fil为Mi的左边界，fir为Mi的右边界，有fir>0且|fil|=fir，则存在i=k，使得对于任意fir均有

fkr≥fir,i=1,2,…,n;k∈{1,2,…,n}

(14)

对所有测量分支取统一量程为

M=[-fkr,fkr]

(15)

4　设计实例

以Stewart并联结构的六维力传感器为例，针对某机器人曲面打磨作业，进行其测量分支量程的确定。

4.1工况确定

某曲面打磨作业的工作周期T为23s，对机器人待测关节进行受力分析后，得到其正常工作时理论上的受力情况，其中,空间外力函数Fx(t),Fy(t),Fz(t)的计算单位为N，函数表达式如下

(16)

(17)

(18)

其函数图像如图2。

图2　待测关节外力时间函数图Fig 2　Time function image of force on the joint under test

空间外力矩函数Mx(t),My(t),Mz(t)的计算单位为N·mm，函数表达式如下

(19)

(20)

Mz(t)=0,0≤t≤23

(21)

函数图像如图3。

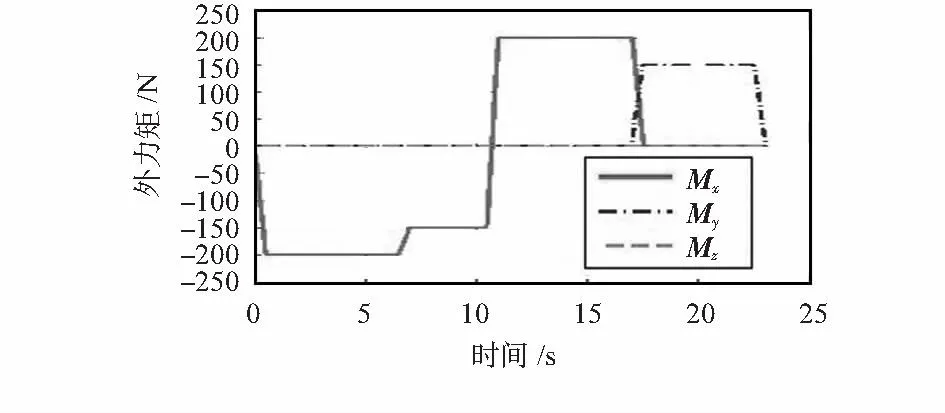
图3　待测关节外力矩时间函数图Fig 3　Time function image of moment of force on the joint under test

式(16)～式(21)确定了待测关节在曲面打磨作业中的外力函数Fw(t)。六维力传感器需满足对Fw(t)的测量要求。

4.2基于时间函数的量程设计

Stewart并联六维力传感器的结构示意图如图4，它由上下2个平台以及6个测量分支组成。上平台为测力平台，下平台为固定平台，在测力平台建立基坐标系O-xyz，Ai(i=1,2,…,6为固定平台上的球铰点在O-xyz中的空间位置，ai(i=1,2,…,6)为测力平台上的球铰点在O-xyz中的空间位置。设置各结构参数如下:H为上下平台间的高度，Ra为上平台球铰点所在圆周的半径，RA为下平台球铰点所在圆周的半径，α和β分别为Aj,Ak和aj,ak(j=1,2,4;k=6,3,5)在其所在圆周中所夹圆心角。

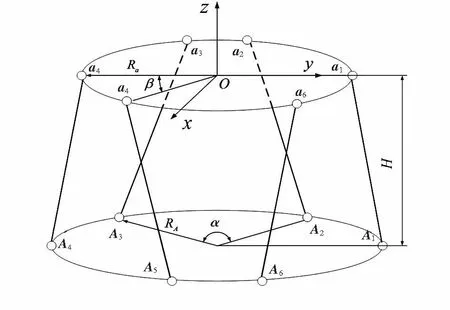
图4　Stewart结构示意图Fig 4　Diagram of Stewart stucture

根据式(1)，建立传感器静力学平衡方程

Fw=G6×6×f6

(22)

根据式(2)，矩阵G6×6可表示为

(23)

根据文献[12]，该传感器结构参数满足如下关系时综合性能最优

(24)

(25)

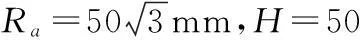
(26)

将外力时间函数Fw(t)和式(26)带入式(9)，应用Matlab计算得到测量分支反作用力变化曲线如图5。

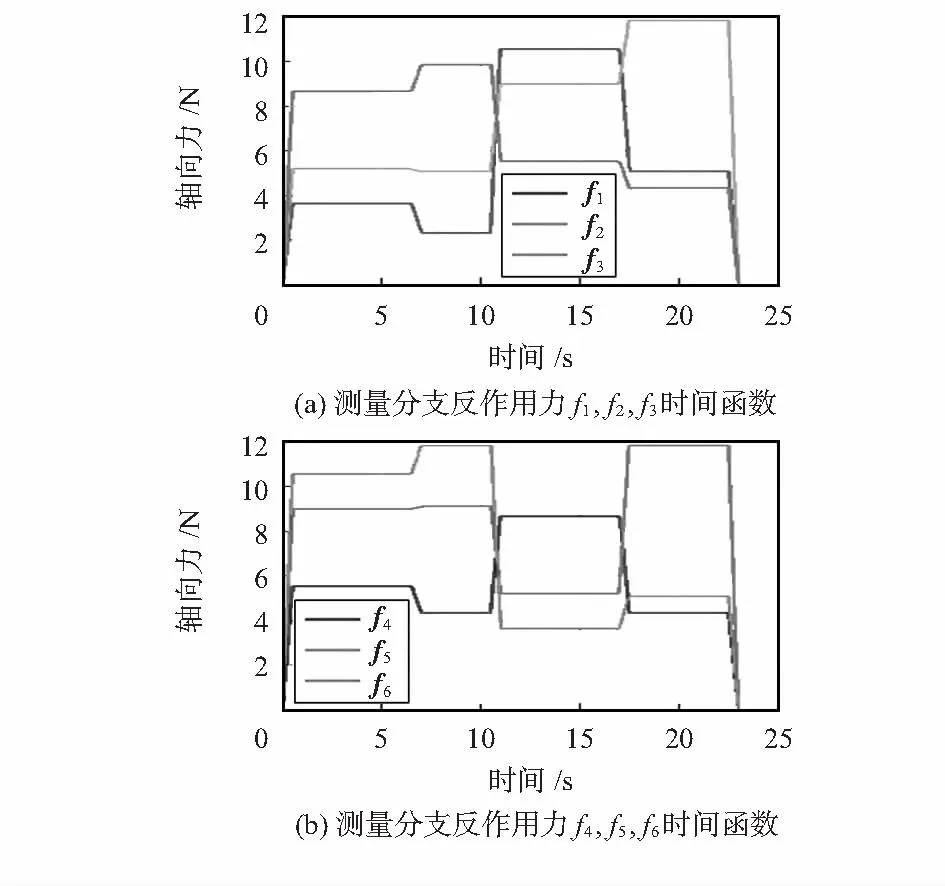
图5　测量分支反作用力时间函数图Fig 5　Time function image of measurement branches reactive force

根据计算结果，由式(11)～ 式(15)，得到测量分支的统一量程为±11.83 N。依此结果进行传感器的加工制造可满足对该机器人在此曲面打磨作业中的力测量要求。提高了六维力传感器的针对性和实用性。

5　结　论

1)推导了并联六维力传感器受六维外力向测量分支反作用力的映射矩阵；

2)结合工况，提出并建立了测量分支反作用力时间函数模型；

3)依据时间函数模型，给出一种可操作性强且通用于并联结构的测量分支量程设计方法；

4) 以Stewart结构为例，针对机器人曲面打磨作业，对测量分支量程进行了设计，验证了时间函数模型的可行性和正确性。

5)研究内容为提高并联六维力传感器的实用性及实现批量生产提供了有效的方法。

[1]王宣银，尹瑞多.基于Stewart机构的六维力/力矩传感器[J].机械工程学报，2008，44(12):118-130.

[2]刘芳华,倪受东,张弛.一种新型大刚度高灵敏度的并联六维力传感器设计研究[J].机械设计与制造,2012(1):23-25.

[3]Gaillet A,Reboulet C. An isostatic six component force and torque sensor[C]∥Proceedings of the 13th International Symposium on Industrial Robots,1983.

[4]Mura A,Six D O F.Displacement measuring device based on a modified Stewart platform[J].Mechatronics,2011,21:1309-1316.

[5]Yao Jiantao，Hou Yulei，Chen Jie，et al.Theoretical analysis and experiment research of a statically indeterminate pre-stressed six-axis force sensor[J].Sensors and Actuators A:Physical，2009，150:1-11.

[6]熊有伦.机器人力传感器的各向同性[J].自动化学报，1996,22(1):10-18.

[7]王航，姚建涛，侯雨雷，等.面向任务的并联结构六维力传感器设计[J].机械工程学报，2011，47(11):7-13.

[8]张景柱，郭凯，徐诚.六维力传感器静态解耦算法应用研究[J].传感器与微系统，2007，26(12):58-59,62.

[9]黄真，孔令富，方跃法.并联机器人机构学理论及控制[M].北京:机械工业出版社，1997:135-137.

[10] 王永茂.矩阵分析[M].北京:机械工业出版社，2005:139-157.

[11] 姚建涛，侯雨雷，毛海峡，等.Stewart结构六维力传感器各向同性的解析分析与优化设计[J].机械工程学报,2009，45(12):22-28.

Design of parallel six-axis force sensor measuring range based on time function*

LIU Wan-yu, WANG Zhi-jun, TIAN Xue-ke, CUI Jian-guo, LI Zhan-xian

(School of Mechanical Engineering,North China University of Science and Technology,Tangshan 063009,China)

Aiming at issues of complex decoupling calculation,difficult to determine range and poor practicability,etc,in process of design and manufacture of parallel six-axis force sensor,mapping matrix from six-dimensional external force in space to measure axial force of branches is deduced with screw theory applied;based on engineering practice,time-function model for measuring axial force of branches by parallel structure six-axis force sensor is proposed and set up;a kind of determination method for measuring range of branches in designated work environment is put forward.Take the Stewart parallel structure for example,aimed at curve polish work,measuring range of branches measuring is determined,then validity and feasibility of time function model are verified.The research contents have important practical value to improve the engineering practicability of parallel structure six-axis force sensor.

six-axis force sensor; measurement branch; time function； measuring range

2015—10—16

国家自然科学基金资助项目(51505124)；华北理工大学研究生创新项目(2015S14)

TH 112.1；TP 242

A

1000—9787(2016)08—0080—04

刘琬钰(1990-)，女，河北邯郸人，硕士研究生，主要研究方向为机器人机构理论，六维力传感器技术。

DOI:10.13873/J.1000—9787(2016)08—0080—04