蒙特卡罗模拟人工自旋冰的退磁过程
2016-08-25虞丽菊孟祥雨李俊琴曹杰峰吴衍青邰仁忠
虞丽菊 孟祥雨 李俊琴 曹杰峰 王 勇 敬 超 吴衍青 邰仁忠
蒙特卡罗模拟人工自旋冰的退磁过程
虞丽菊1孟祥雨2李俊琴2曹杰峰2王 勇2敬 超1吴衍青2邰仁忠2
1(上海大学 物理系 上海 200444)2(中国科学院上海应用物理研究所 张江园区 上海 201204)
近年来,人工自旋冰(Artificial spin ice, ASI)因具有潜在的应用价值以及理论研究价值而倍受关注,成为磁学领域的研究热点之一。以往的研究集中在Square和Kagome两种晶格结构,由于能量势垒和阻挫的大量存在,实验上难以通过退磁等方法达到其内部相互作用决定的能量基态。本文基于Kagome晶格结构提出了一种新的人工自旋冰结构,并基于蒙特卡罗模拟了三种不同的退磁方法对体系能量的影响。结果表明,退磁过程中旋转磁场方向可更有效地降低体系能量,并诱导多种磁结构的出现。
人工自旋冰,蒙特卡罗模拟,退磁
自旋冰是Harris等[1]在研究钛酸盐Ho2Ti2O7时,发现的一种自旋阻挫新象。该体系中晶格结构由四面体基本单元构成,每个Ho原子周围存在4个Ti原子,其中两个自旋指向四面体内部,另外两个指向外部,遵循“冰法则”排列[2]。这种钛酸盐存在绝对零度剩余熵和阻挫现象,并且其剩熵幅值与Pauling预言的冰氢剩熵幅值大小一致[3],因此称之为自旋冰。
阻挫指体系中等价单元之间存在相互竞争,但每一方都无法取得支配地位的现象,广泛存在于自然界及凝聚态体系中。研究阻挫现象对于计算机错误校正码[4]、蛋白质动力学[5]以及生物神经网络[6]的模型研究具有重要帮助。磁学中主要研究几何阻挫[7],如图1所示,几何晶格结构和近邻交换作用不相容,位于格点的磁矩无论如何排列,都不能满足所有相邻磁矩间相互作用能极小,形成阻挫。

图1 几何阻挫结构示意图Fig.1 Structure charts of geometrical frustration.
研究表明,阻挫的存在导致了自旋冰体系基态高度简并,是凝聚态领域中十分重要的研究体系。然而,钛酸盐等天然自旋冰存在样品制备困难、表征平台少以及分辨能力有限等缺点,导致相关的研究受阻。2006年,Wang等[8]采用电子束刻蚀的方法,制备了世界上首个人工自旋冰体系。该课题组在硅片基底上沉积单个尺寸为220 nm×80 nm× 25nm的坡莫合金,形成准二维Square晶格阵列,并使用原子力显微镜(Atomic Force Microscope, AFM)和磁力显微镜(Magnetic Force Microscope, MFM)观测了阵列的磁结构成像。磁体为沿矩形长轴方向排列的单畴态,每4个磁体形成一个阻挫作用点。图2为Square和Kagome两种人工自旋冰体系的晶格示意图。
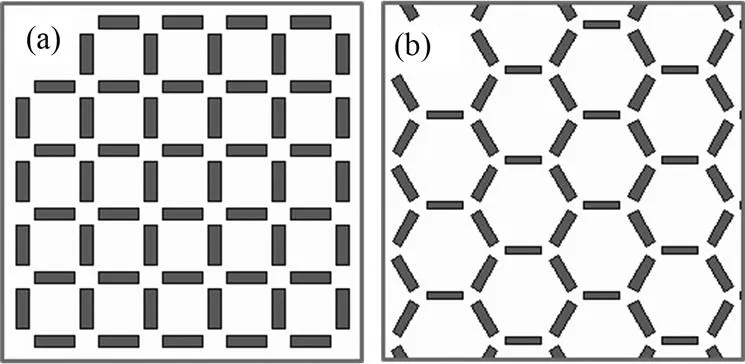
图2 两种人工自旋冰结构示意图(a) Square晶格,(b) Kagome晶格Fig.2 Two Lattice structures of ASI.(a) Square lattice, (b) Kagome lattice
该项工作实现了自旋冰体系的人工制备和成像观测,很大程度上降低了阻挫现象的研究难度。此外,这种有序的周期结构可作为多体相互作用系统的统计力学研究平台[9],其内部单元之间存在很强的作用力,磁耦合能和阻挫的相关研究还将有望给图案化磁记录技术提供参考。
实现以上研究和应用首要解决的问题就是寻找人工自旋冰体系的基态。理论认为,体系总是在能量最小时处于平衡稳定的状态,而总能量是由内部单元耦合相互作用决定的。由于阻挫和势垒的大量存在,制备完成的样品往往处于无序的能量激发态。使用传统的退火处理效果不甚理想,原因在于自旋冰体系近邻磁矩间的耦合作用能高达105K[10],要在室温附近对其进行退火处理难度很大。Mrogan等[11]通过在样品生长过程中退火诱导Square自旋冰体系达到了有序基态。不少工作对自旋冰体系的退磁处理进行了研究,Wang等[12]认为如果在变换磁场的同时旋转样品,可使Square体系较大范围接近能量基态。Mengotti等[13]使用类似的方法研究了Kagome自旋冰的退磁,结果表明,对单个六边形进行退磁处理,较易出现自旋首尾相接的能量基态,但随着六边形的数目增大,近邻磁体形成阻挫,很难再出现这种基态。
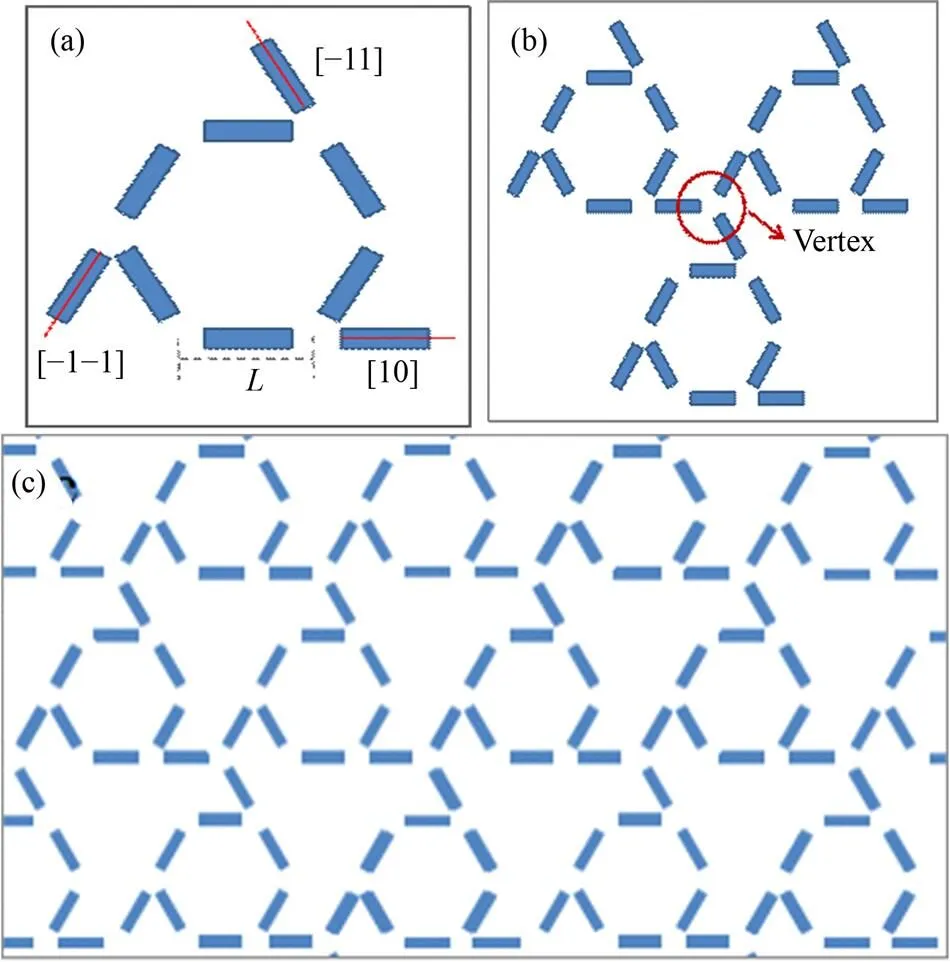
图3 涡旋人工自旋冰结构示意图(a) 单元结构,中间形成六边形,另外三个磁体分别沿[10],[‒11],[‒1‒1]三个方向,(b) 每三个涡旋单元交汇处形成一个阻挫作用点,(c) 晶格示意图Fig.3 Structure charts of Vortex ASI.(a) Unit structure, there is a hexagon in the middle, the other three along [10], [‒11], [‒1‒1] respectively,(b) Every three units forming a frustrated Vortex,(c) Lattice structure
为降低阻挫对体系的干扰,我们基于Kagome晶格设计了一种涡旋自旋冰结构,并采用蒙特卡罗模拟方法来研究三种不同的退磁手段对体系的退磁效果。如图3所示,每个涡旋结构单元由9个矩形坡莫合金磁体组成,磁体尺寸为220 nm×80nm× 25nm。单元中间6个磁体形成一个六边形结构,而在单元交接处,每3个磁体形成一个阻挫作用点。我们模拟了包括21×21个与41×41个涡旋单元结构的体系,结果基本相同,因此以下以21×21为例进行分析。
由于矩形磁体沿长轴方向形成单畴态,有两种取向,可近似为伊辛自旋。对于涡旋单元结构中心的六边形,可以形成26共64种自旋组态。然而近邻磁体之间存在耦合作用,当涡旋结构处于能量基态时,将形成自旋首尾相接的两种磁组态:自旋顺时针(Type-CW)和自旋逆时针(Type-CCW),是两种简并的能量基态。对于阻挫作用点,其基态自旋结构为“两进一出”或“两出一进”,共有6种简并态。激发态呈现为自旋三个朝内(Type-In)或者三个朝外(Type-Out),是两种能量简并态(图4)。体系处于理想基态时(图6(a)),六边形形成Type-CW与Type-CCW交替排列,在阻挫作用点,则是“两进一出”和“两出一进”交替排列,而不会出现Type-In或Type-Out的激发态结构。

图4 涡旋人工自旋冰的4种典型结构Fig.4 Four typical structures of Vortex ASI.
1 蒙特卡罗模拟
本文基于蒙特卡罗模拟三种不同的退磁方法对体系的退磁效果。其主要思想是:假设整个体系共有个自旋构成一个组态,随机分配给体系一个初始态,假设体系中的部分自旋发生翻转而产生新的组态,通过近邻磁耦合作用计算能量变化Δ及玻尔兹曼权重指数:0=exp(‒Δ/B),决定是否翻转,其中:B为玻尔兹曼常数,为温度,模拟中取为300 K;不断重复上述过程,直到体系能量趋于稳定。对于近邻磁体之间的相互作用,本文选用磁偶极子模型[10]。该模型将每个磁体看成理想的点磁矩,磁矩之间的作用能大小为:
式中:0为玻尔兹曼常数;和指相互作用的两个磁矩,其值由坡莫合金的磁化强度=800×103A∙m‒1计算得到;代表两个磁矩中心的距离矢量。然而,当近邻磁矩间距较小时,磁体的体积不可忽略。本文改进了磁偶极子模型,将每个220 nm× 80nm×25 nm的坡莫合金磁体细分成许多个大小为22 nm×10 nm×5 nm的单元,总的近邻磁体之间的耦合能采用求和的方式得到。施加外磁场时,还需考虑体系的塞曼能:
由于两个磁体之间的耦合能会随着它们之间的距离增大而快速减小。对于一个给定的磁体,当另一个磁体与它之间的耦合能小于来自最近邻磁体耦合能的3%时,忽略不计。对于单个矩形磁体,由于形状各向异性能的影响,退磁过程中需要克服一定的能量势垒才能发生翻转。根据文献[14],对于尺寸为220 nm×80 nm×25 nm的坡莫合金,形状各向异性能大小为:0=3.17´10‒18J(约为2.3´105K)。考虑涨落的存在,计算中对每个磁体的势垒进行随机分配:0j0,其中:为无量纲随机分布,期望值=1,标准差选取了0.1‒0.3之间的一系列参数进行试验,对结果的影响很小,最终选取=0.25。
本工作中,基于能量最小原理的蒙特卡罗模拟计算包含以下具体步骤:1) 给体系随机分配一个初始状态;2) 随机假设每个单元中的个磁体进行翻转,其中服从概率分布:P=(1/2),(=1,2,…,9);3) 计算翻转所需的能量变化:Δ=E‒E+Σ0,其中:E和E分别为翻转后和翻转前的体系总能量。如果Δ≤0,表明翻转后体系能量降低,发生翻转,回到第2步;4) 如果Δ>0,表明翻转后体系能量将增加,计算玻尔兹曼权重指数:0=exp(‒Δ/B),产生一个随机数,∈(0,1),如果0>,发生翻转,回到第2步;5) 如果0≤,不发生翻转,回到第2步;6) 多次重复以上过程,直到系统达到稳定的能量状态。
本工作中我们一共采用三种退磁方法。方法1(图5(a)):首先沿[10]方向(图3)施加0.15 T的初始饱和磁场,等待一定的时间使系统达到平衡,然后快速变化到反方向,每次反向磁场的大小都减少一定幅度Δ,其值等于初始饱和磁场除以循环总数,待退磁完成所有的循环,磁场刚好降到零。方法2(图5(b)):在每个循环中,磁场大小按一定的步长变化,达到最大值时无需等待系统平衡,直接进行下一个循环。方法3(图5(c)):磁场的角度沿顺时针(或逆时针)方向匀速变化,同时磁场的大小按一定的步长均匀减小,直至磁场为零。
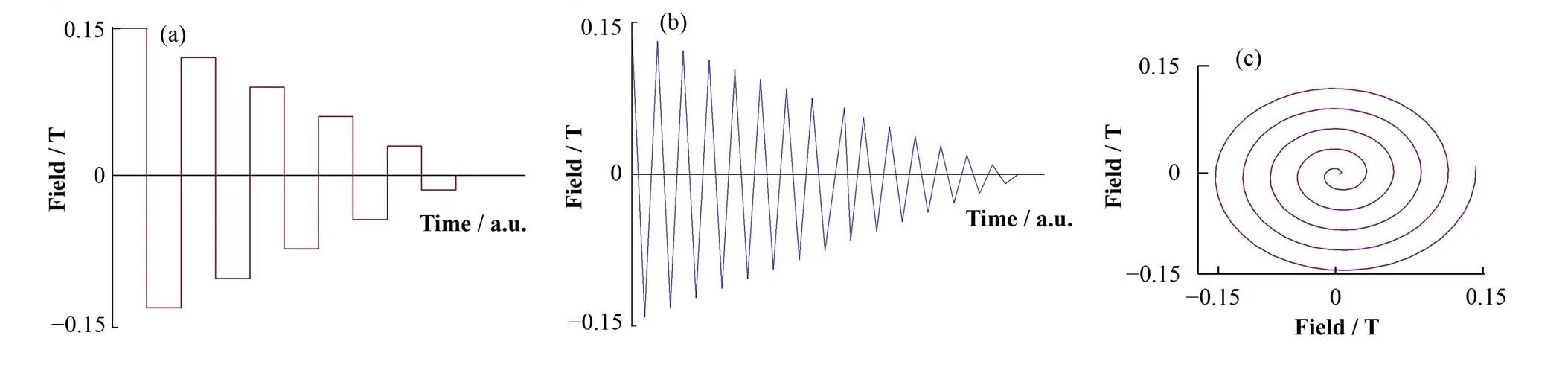
图5 三种退磁方法示意图(a) 方法1,(b) 方法2,(c) 方法3Fig.5 Demagnetization scheme.(a) Method 1, (b) Method 2, (c) Method 3
为寻找最优的参数,我们对每种方法采取了一系列的循环次数和步数进行模拟,并以退磁后体系的总能量为指标,比较而得较优参数。对于方法1,选取了50000、100000、150000、200000这4种循环次数,体系的退磁总能量先降低,然后趋于稳定,磁场的大小快速变化,步数为1;方法2的循环次数取1000,步数分别取100‒400,间隔为100,随着步数增大,退磁总能量并没有降低,取100即可;而对于方法3,循环次数取500和1000,步数分别取180‒720,间隔为180,结果表明当循环次数取1000,步数取540时,退磁总能量已降到最低,更精细化的参数对结果几乎没有影响。
2 结果与讨论
首先,选取晶格常数=500 nm的体系进行模拟计算,得到三种方法退磁后体系的自旋组态(图6)。图6(a)为理想的体系基态,中间六边形形成Type-CW与Type-CCW交替排列的磁结构,两种结构出现的频率都为50%,在阻挫作用点,则是“两进一出”和“两出一进”交替排列。与有序基态相比,方法3更容易形成Type-CW和Type-CCW两种基态结构,方法2次之,由于近邻单元之间存在复杂的相互作用,Type-CCW和Type-CW并不是交替排列的,而有可能同一类型连续出现,这是由于近邻磁矩之间存在较强的耦合作用能,引起磁体连续翻转造成的。图7对三种方法退磁后体系中4种结构的出现频率进行了统计,对应图6(b)‒(d)。在理想情况下的最低能量状态(图6(a)),每一个六角结构均为CW或者CCW,CW和CCW交替出现,各自占六角结构总数的50%。在实际的退磁过程中,体系中磁体的翻转是一个涨落过程,不可能达到最低能量状态,有些六角结构既不是CW也不是CCW,而是一种无序状态。这种情况在方法1中尤其明显,只有约10%的六角结构是CW和CCW;方法2比方法1好一点,CW和CCW在所有六角结构中的占比达到了20%左右;方法3最理想,达到了40%左右,体系的总能量也最接近基态,同时由于大量Type-CW和Type-CCW结构的出现,诱导近邻的阻挫作用点出现Type-In以及Type-Out的能量激发态,在所有三角结构中的占比接近10%。比较三种方法退磁后的体系总能量(图8),方法3仍最大程度接近体系的基态能量1.947×10‒15J。


图6 蒙特卡罗计算体系的基态自旋排布,以及三种方法退磁后的自旋排布,对应图4中的4种结构类型(a) 理想基态,(b) 方法1,(c) 方法2,(d) 方法3Fig.6 Structure chart for ground state and demagnetization results of three methods corresponding to Fig.4.(a) Ground state, (b) Method 1, (c) Method 2, (d) Method 3
另外在图7中可以看出,在三种退磁方法中,Type-CW和Type-CCW、Type-In和Type-Out的数目并不严格相等。这是由于磁体的翻转具有随机性,进行特定的退磁过程后,会产生对称性破缺,各种结构的数目不相等,体系不是处于最低能量状态。并且由于每个磁体的翻转存在势垒,当热涨落的能量不足以克服势垒时,整个体系会达到平衡状态,这种平衡状态不具有严格的对称性。

图7 三种方法退磁后4种结构类型的统计频率Fig.7 Statistical frequency of four types by three methods.
随后调整体系的晶格常数为=400 nm和=600 nm,同样模拟了三种方法的退磁效果。对于这两种晶格参数的体系,方法3仍然是最理想的退磁方法,能将体系总能量降得最低(表1)。统一采用方法3退磁后,对等于400 nm、500 nm、600 nm的体系进行比较,4种结构类型的分布如图9所示。当=400 nm时,近邻磁体之间距离更近,相互作用更强,退磁后容易形成能量较低的两种结构类型Type-CW和Type-CCW,频率在40%左右,几乎不会出现能量激发态结构。随着晶格常数增大,Type-CW和Type-CCW的出现频率减小,Type-In和Type-Out两种激发态结构的出现频率则在增大,=600 nm时,分别达到12.5%和12.8%。上述结果表明,晶格常数可有效地调控内部相互作用,后者是驱动体系抵达有序能量基态的主要因素,而退磁可以部分消除能量势垒的影响,某种程度上诱导自旋实现“自由翻转”,使体系更容易接近能量基态。

图8 三种方法退磁后体系的总能量Fig.8 System energy after demagnetization by three methods.
表1 不同晶格常数的体系退磁后的总能量
Table 1 System energy of different lattices after demagnetization.
晶格常数
/ nm
方法1
Method 1 / 10J
方法2
Method 2 / 10J
方法3
Method 3 / 10J
最低能量
Min energy / 10J
400
‒4.040
‒4.143
‒4.159
‒4.227
500
‒1.799
‒1.811
‒1.818
‒1.947
600
‒9.842
‒9.761
‒9.890
‒1.094
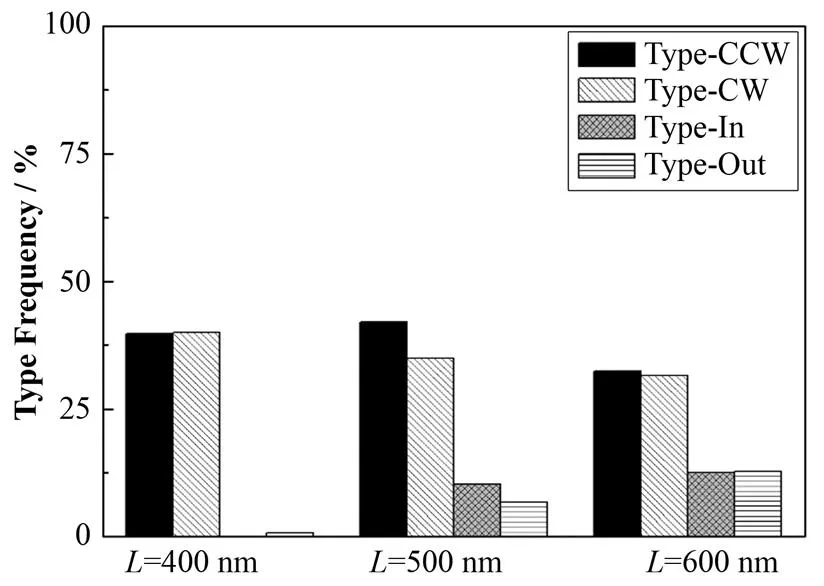
图9 方法3退磁后4种结构的频率分布Fig.9 Statistical frequency by method 3.
3 结语
本文基于蒙特卡罗方法模拟了三种方法对人工自旋冰体系的退磁效果,通过调整外磁场的循环次数、步数以及场方向,确定旋转磁场退磁为最佳退磁方案。选取循环次数为1000,步数为540,磁场沿面内旋转,当一个循环完成时回到原点。作为消除磁性材料势垒的常用方法,退磁可使人工自旋冰体系中的自旋磁矩克服能量障碍,实现一定程度的“自由翻转”,最终通过近邻磁矩间的相互作用决定体系的自旋组态。无论是作为多体相互作用系统的统计力学平台,还是图案化磁记录技术以及阻挫现象的研究体系,退磁处理都是人工自旋冰研究过程中首要的、关键的一步。我们将在随后的工作中采用电子束曝光等手段[15]制备本文提出的人工自旋冰结构,对其进行磁性表征,研究其丰富的物理性质并与本文的理论结果进行比较。
1 Harris M J, Bramwell S T, Mcmorrow D F,. Geometrical frustration in the ferromagnetic pyrochlore Ho2Ti2O7[J]. Physical Review Letters, 1997, 79(13): 2554‒2557. DOI: 10.1103/PhysRevLett.79.2554
2 Wills A S, Ballou R, Lacroix C. Model of localized highly frustrated ferromagnetism: the kagomspin ice[J].2002, 66(14): 144407. DOI: 10.1103/ PhysRevB.66.144407
3 Pauling L. The structure and entropy of ice and of other crystals with some randomness of atomic arrangement[J]. Journal of the American Chemical Society, 1935, 57(12): 2680‒2684. DOI: 10.1021/ja01315a102
4 Soulas N. Spin-glass models as error-correcting codes[J]. Nature, 1989, 333(6227): 693‒695. DOI: 10.1038/ 339693a0
5 Bryngelson J D, Wolynes P G. Spin glasses and the statistical mechanics of protein folding[J]. Proceedings of the National Academy of Sciences of the United States of America, 1987, 84(21): 7524‒7528. DOI: 10.1073/pnas. 84.21.7524
6 Toulouse G, Dehaene S, Changeux J P. Spin-glass model of learning by selection[J]. Proceedings of the National Academy of Sciences of the United States of America, 1986, 83(6): 1695‒1698. DOI: 10.1073/pnas.83.6.1695
7 范诚. 磁阻挫材料RMnO3和Dy2Ti2O7的单晶生长与低温物性[D]. 合肥: 中国科学技术大学, 2013
FAN Cheng. Crystal growth and low-temperature physical properties of magnetically frustrated RMnO3and Dy2Ti2O7[D]. Hefei: University of Science and Technology of China, 2013
8 Wang R F, Nisoli C, Freitas R S,. Artificial ‘spin ice’ in a geometrically frustrated lattice of nanoscale ferromagnetic islands[J]. Nature, 2006, 439(7074): 303‒306. DOI: 10. 1038/nature04447
9 Lammert P E, Ke X L, Li J,. Direct entropy determination and application to artificial spin ice[J]. Nature Physics, 2010, 6(10): 786‒789. DOI: 10.1038/ NPHYS1728
10 Qi Y, Brintlinger T, Cumings J. Direct observation of the ice rule in an artificial Kagome spin ice[J]. Physical Review B, 2008, 77(9): 094418. DOI: 10.1103/PhysRevB. 77.094418
11 Mrogan J P, Stein A, Langrige S,. Thermal ground-state ordering and elementary excitations in artificial magnetic square ice[J]. Nature Physics, 2010, 7: 75‒79. DOI: 10.1038/NPHYS1853
12 Wang R F, Li J, McConville W,. Demagnetization protocols for frustrated interacting nanomagnet arrays[J]. Journal of Applied Physics, 2007, 101(9): 1‒15. DOI: 10.1063/1.2712528
13 Mengotti E, Heyderman L J, Rodríguez A F,. Building blocks of an artificial kagome spin ice: photoemission electron microscopy of arrays of ferromagnetic islands[J]. Physical Review B, 2008, 78: 144402. DOI: 10.1103/PhysRevB.78.144402
14 Moller G, Moessner R. Artificial square ice and related dipolar nanoarrays[J]. Physical Review Letters, 2006, 96(23): 237202. DOI: 10.1103/PhysRevLett.96.237202
15 陈媚, 于怀娜, 赵俊, 等. 光子晶体制备方法对同步辐射闪烁体探测器成像分辨率的影响[J]. 核技术, 2015, 38(7): 070101. DOI: 10.11889/j.0253-3219.2015.hjs.38. 070101
CHEN Mei, YU Huaina, ZHAO Jun,. Effect of photonic crystal prepared by different methods on the spatial resolution of scintillator-based synchrotron radiation imaging detector[J]. Nuclear Techniques, 2015, 38(7): 070101. DOI: 10.11889/j.0253-3219.2015.hjs.38. 070101
国家自然科学基金(No.11475251、No.11275255、No.11225527、No.5137111)、上海市科委基础研究重点项目(No.13JC402400)资助
Supported by National Natural Science Foundation of China (No.11475251, No.11275255, No.11225527, No.5137111), and the Key Project of Shanghai Municipal Science and Technology Commission (No.13JC402400)
Monte Carlo simulation on demagnetization of artificial spin ice
YU Liju1MENG Xiangyu2LI Junqin2CAO Jiefeng2WANG Yong2JING Chao1WU Yanqing2TAI Renzhong2
1(Department of Physics, Shanghai University, Shanghai 200444, China)2(Shanghai Institute of Applied Physics, Chinese Academy of Sciences, Zhangjiang Campus, Shanghai 201204, China)
Background: Recently, the artificial spin ice (ASI) draws a wide attention for its exotic phenomenon and potential applications. Previous works mainly studied the Square and Kagome lattice systems, and extensive researches concentrated upon how to achieve the ground state. It turned out to be experimentally difficult to get the absolute ground state of Kagome ASI because of the high frustration. Purpose: Here we propose a new structure based on Kagome lattice, which is just locally frustrated. In order to get good approximation of its ground state, we employed a Monte Carlo simulation on demagnetization process with three methods. Methods: The Monte Carlo simulation was carried on a system including 21×21 cells, and an extra field had been employed to drive the spins overturning. Results & Conclusion: It turned out that the rotating magnetic field was more effective to get to the ground state, and induced the emergence of various magnetic structures.
ASI, Monte Carlo simulation, Demagnetization
YU Liju, female, born in 1989, graduated from Guangxi University in 2013, master student, focusing on magnetic nanostructure
WANG Yong, E-mail: wangyong@sinap.ac.cn; WU Yanqing, E-mail: wuyanqing@sinap.ac.cn; TAI Renzhong, E-mail: tairenzhong@sinap.ac.cn
TL65,O469
10.11889/j.0253-3219.2016.hjs.39.060502
虞丽菊,女,1989年出生,2013年毕业于广西大学,现为硕士研究生,研究领域为磁性纳米结构
王勇,E-mail: wangyong@sinap.ac.cn;吴衍青,E-mail: wuyanqing@sinap.ac.cn;邰仁忠,E-mail: tairenzhong@sinap.ac.cn
2016-01-25,
2016-04-12
