RC框架结构基于构件损伤的抗震性能评估研究*1

张耀庭，杜晓菊，杨　力

(1．华中科技大学 土木工程与力学学院，湖北 武汉　430074；2．成都基准方中建筑设计有限公司，四川 成都　610021 )



RC框架结构基于构件损伤的抗震性能评估研究*1

张耀庭†，杜晓菊1,2，杨力1

(1．华中科技大学 土木工程与力学学院，湖北 武汉430074；2．成都基准方中建筑设计有限公司，四川 成都610021 )

首先根据钢筋混凝土柱的拟静力试验结果，探讨王东升的修正Park-Ang模型的适用性；然后基于构件层次的结构损伤指标为地震需求参数，对钢筋混凝土框架结构进行了基于IDA的易损性分析，并结合基于最大层间位移角的分析结果，探讨了结构基于损伤的抗震性能评估方法的可行性.结果表明：王东升提出的修正Park-Ang模型考虑了加载路径的影响，能较准确地反映首次超越破坏后累积损伤的发展过程，且总体上判别试件损伤状态的准确性相对较高；基于损伤的IDA能较好地反映整体结构及局部的损伤发展过程、结构的失效破坏机制，能准确地判别结构的薄弱环节，但结构损伤指标会产生超出1.0的情况，不能很好地体现损伤指标原始定义的基本含义；相较结构基于最大层间位移角的抗震性能评估结果，基于结构损伤的抗震性能评估方法综合考虑了结构的响应与自身的能力，更全面地评估了结构的性能水准，能预测结构在不同地震强度下各性能状态的失效概率.

钢筋混凝土框架;修正Park-Ang损伤模型;增量动力分析;易损性分析;柱拟静力试验

随着基于性能的抗震设计理论与损伤模型研究的发展，通过损伤模型来量化结构性能指标，实现基于损伤的抗震性能评估方法将成为必然.目前，基于钢筋混凝土结构在地震作用下的两种破坏模式，国内外学者采用不同的响应参数建立了各种各样的损伤模型，包括基于变形、退化、能量、低周疲劳及其组合形式的损伤模型，但没有一个统一、普遍适用的损伤模型.其中，基于变形与能量的Park-Ang损伤模型在地震工程领域中得到较多的应用和研究，根据该模型的缺陷与不足，Kunnath[1]、Kumar[2]、Chai[3]、欧进萍[4]、牛荻涛[5]和吕大刚[6]等学者从不同角度对其进行了修正和改进.本文首先根据钢筋混凝土柱的拟静力试验结果，探讨王东升的修正Park-Ang模型[7]的适用性.然后，以结构损伤指标为地震需求参数，对钢筋混凝土框架结构进行了基于IDA方法的易损性分析，并结合基于最大层间位移角的分析结果，探讨了结构基于损伤的抗震性能评估方法的可行性.

1　钢筋混凝土柱的拟静力试验

1.1钢筋混凝土柱的拟静力试验

1．1．1试件设计

按照我国现行规范设计了2根相同的钢筋混凝土柱试件，分别为C1，C2.柱净高为1 050 mm，保护层厚度为20 mm，剪跨比为3.5，设计轴压比为0.15，配筋率为1.7%，配箍率为1.16%，试件详细尺寸与配筋信息如图1所示.混凝土强度等级为C40，纵筋、箍筋强度等级分别为HRB400,HPB300，混凝土立方体抗压强度的实测值为48.20 MPa，轴心抗压强度为36.63 MPa，试验轴压比为0.076，钢筋的实测性能指标见表1.

1．1．2试验加载装置及加载制度

试件采用悬臂自由端加载，如图2，图3所示.竖向液压千斤顶通过滚轴装置与反力架横梁相连，以确保与试件一起平动，水平推拉液压千斤顶固定在反力墙上，通过连接板作用于试件顶部加载中心线上.首先通过竖向液压千斤顶一次性施加竖向荷载至预定值(250 kN)，并使其在试验过程中保持稳定，然后通过水平推拉液压千斤顶施加水平反复荷载，并采用位移控制加载.试件C1的位移幅值分别为柱净高的0.5%,1.0%,1.5%，2.0%,2.5%,3.0%,3.5%和4.0%，每级荷载循环两次；试件C2分三级等幅值加载，位移幅值分别为柱净高的2.0%，3.0%和3.5%，每级荷载循环10次.当试件的承载力下降到最大承载力的85%时，停止试验.

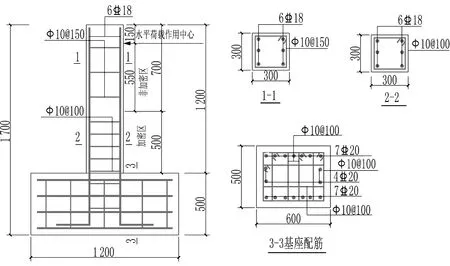
图1　试件尺寸与配筋Fig.1　Dimension and reinforcement assembly of specimens表1　钢筋的力学性能指标Tab.1　Mechanical performance indexes of steels

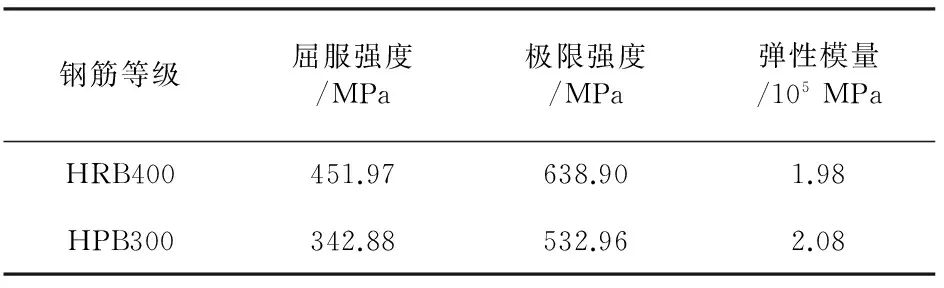
钢筋等级屈服强度/MPa极限强度/MPa弹性模量/105MPaHRB400451.97638.901.98HPB300342.88532.962.08

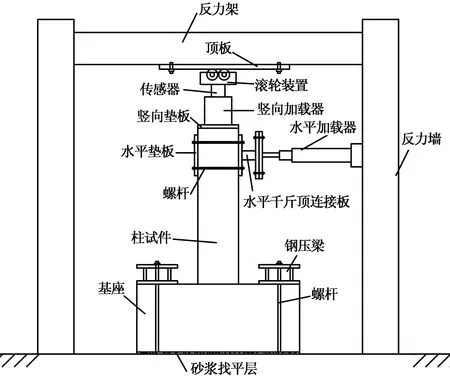
图2　试验加载装置示意图Fig.2　Loading equipment diagram of the test

图3　试验实际加载装置Fig.3　Actual loading equipment of the test

1．1．3试验现象与结果

随着加载的进行，柱底产生肉眼可见的裂纹，并逐渐向上扩展、延伸.试件C1加载至第3周时，柱底出现水平贯通的裂纹，柱身侧面产生斜裂纹，试件产生轻微破坏；加载至第8周时，柱底出现起皮掉皮现象，侧面产生多条交叉斜裂缝，裂缝持续扩展，试件产生中等破坏；加载至第14周时，柱底出现多条贯通裂缝且裂缝显著变宽，柱底保护层起拱，柱脚混凝土大块脱落，试件产生严重破坏；加载至第17周时，柱底混凝土大面积压溃崩落，箍筋外露，纵筋压屈向外鼓出，试件产生倒塌破坏，试件C1的破坏形态如图4所示.

试件C2加载至第2周时，试件下部多处开裂，柱底产生水平贯通的裂纹，侧面产生交叉斜裂纹，反向加载时裂纹闭合，试件产生轻微破坏；第3～10周循环加载中，原有裂缝缓慢开展，无其他明显的破坏现象产生；加载至第11周时，柱底产生竖向裂缝并出现起皮掉皮现象，侧面斜裂缝延伸至柱底，试件产生中等破坏；加载至第15周时，柱底保护层混凝土脱落，侧面交叉裂缝宽度显著增大，试件产生严重破坏；加载至第21周时，试件严重倾斜，柱下部混凝土严重脱落，纵筋屈曲，试件产生倒塌破坏，第22～23周加载过程中，试件强度急剧下降，失去承载能力.试件C2的破坏形态如图5所示.试件C1，C2的水平荷载与顶点位移(P-δ)滞回曲线如图6所示.

图4　试件C1的破坏形态Fig.4　Failure mode of specimen C1

图5　试件C2的破坏形态Fig.5　Failure mode of specimen C2

δ/mm (a) C1

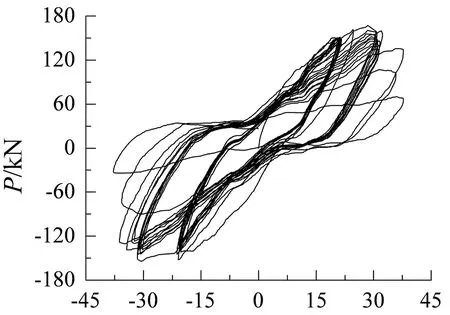
δ/mm (b) C2图6　试件C1，C2的滞回曲线Fig.6　Hysteretic curves of specimens C1 and C2

1.2Kunnath试验简介

1996年，Kunnath等对2组共12根1/4比例的圆截面钢筋混凝土桥墩试件分别进行了拟静力试验和振动台试验[8].由于本文试验数量有限，选用PEER数据库提供的6根试件(A1～A6)的拟静力试验结果作为补充.各试件的有效高度均为1 370 mm，截面直径均为305 mm；纵筋配置21φ9.5 mm，屈服强度为448.0 MPa，配筋率为2.04%；箍筋配置φ4@19 mm，屈服强度为434.0 MPa，配箍率为0.96%，其他信息如表2所示.

表2　试件A1～A6的基本信息Tab．2　Basic information of specimens A1 to A6

试件A1～A6的加载制度分别为：

A1：单调加载至失效，其极限位移为150 mm；

A2：位移幅值分别为1.0%，1.5%，2.0%，2.5%，3.0%，4.0%，5.0%和6.0%，每级荷载循环3周，不同位移幅值之间施加1周0.5%的循环荷载；

A3～A6：均为等幅值加载，位移幅值分别为2.0%，4.0%，5.5%和7.0%.

本文仅对试件A2～A6进行分析，其力-位移(P-δ)滞回曲线如图7所示.

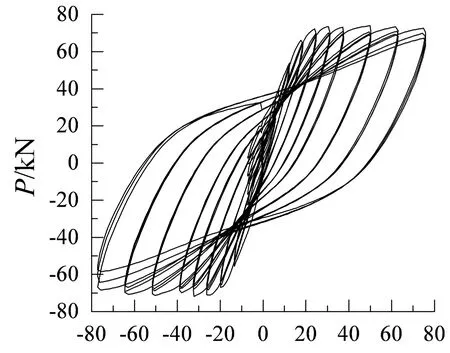
δ/mm (a) A2

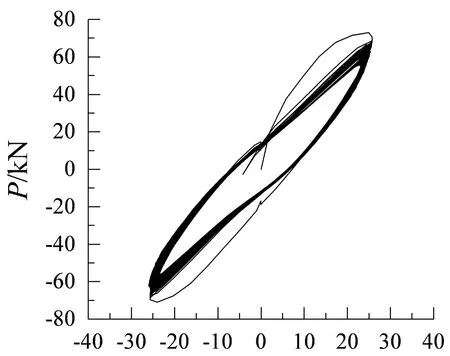
δ/mm (b) A3

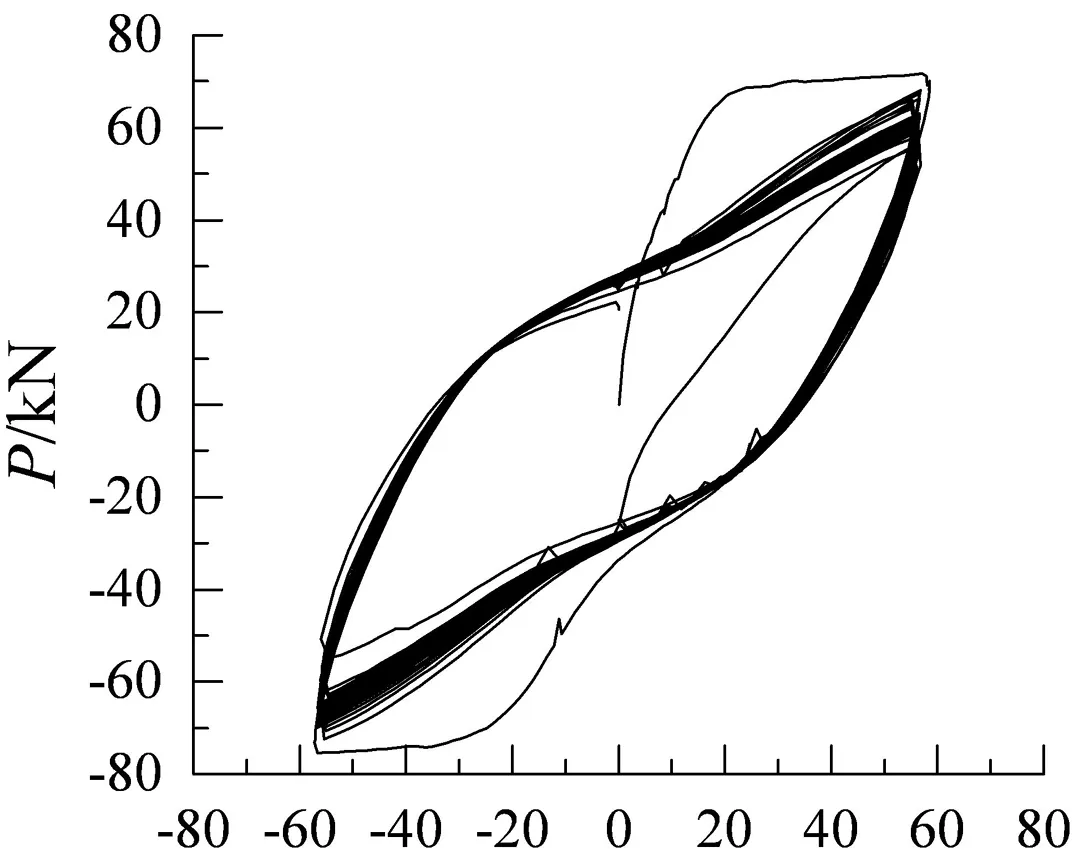
δ/mm (c) A4

δ/mm (d) A5

δ/mm (e) A6图7　试件A2～A6的滞回曲线Fig.7　Hysteretic curves of specimens A2 to A6

2　修正Park-Ang损伤模型研究

2005年，王东升等通过钢筋混凝土构件的拟静力试验结果指出当位移延性系数较小时，Park-Ang损伤模型不能正确反映构件极限滞回耗能与位移延性系数的关系，不能有效地评估构件的损伤状态[7].其在能量项引入加权因子βi来考虑加载路径的影响，修正了该损伤模型，如式(1)，(2)所示，各损伤状态对应的损伤指标范围如表3所示.

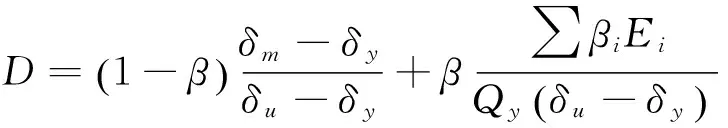
(1)

(2)

式中：Ei为第i个滞回环的塑性耗能；βi为加载路径有关的加权因子；β为组合因子；γE为能量等效系数，取γE=0.1；μ0为临界延性系数，可取为2～3，取μ0=2.5；μi为当前构件最大位移对应的延性系数；μp为单调加载下极限位移对应的延性系数.

表3　不同损伤状态对应的损伤指标范围Tab.3　Damage index range of different damage states

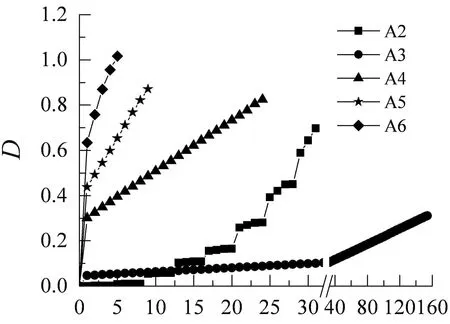
采用该损伤模型评估试件A2～A6，C1，C2在试验过程的损伤程度，损伤发展曲线(T-D)如图8所示，各试件在加载过程中的破坏现象及对应损伤指标如表4所示.

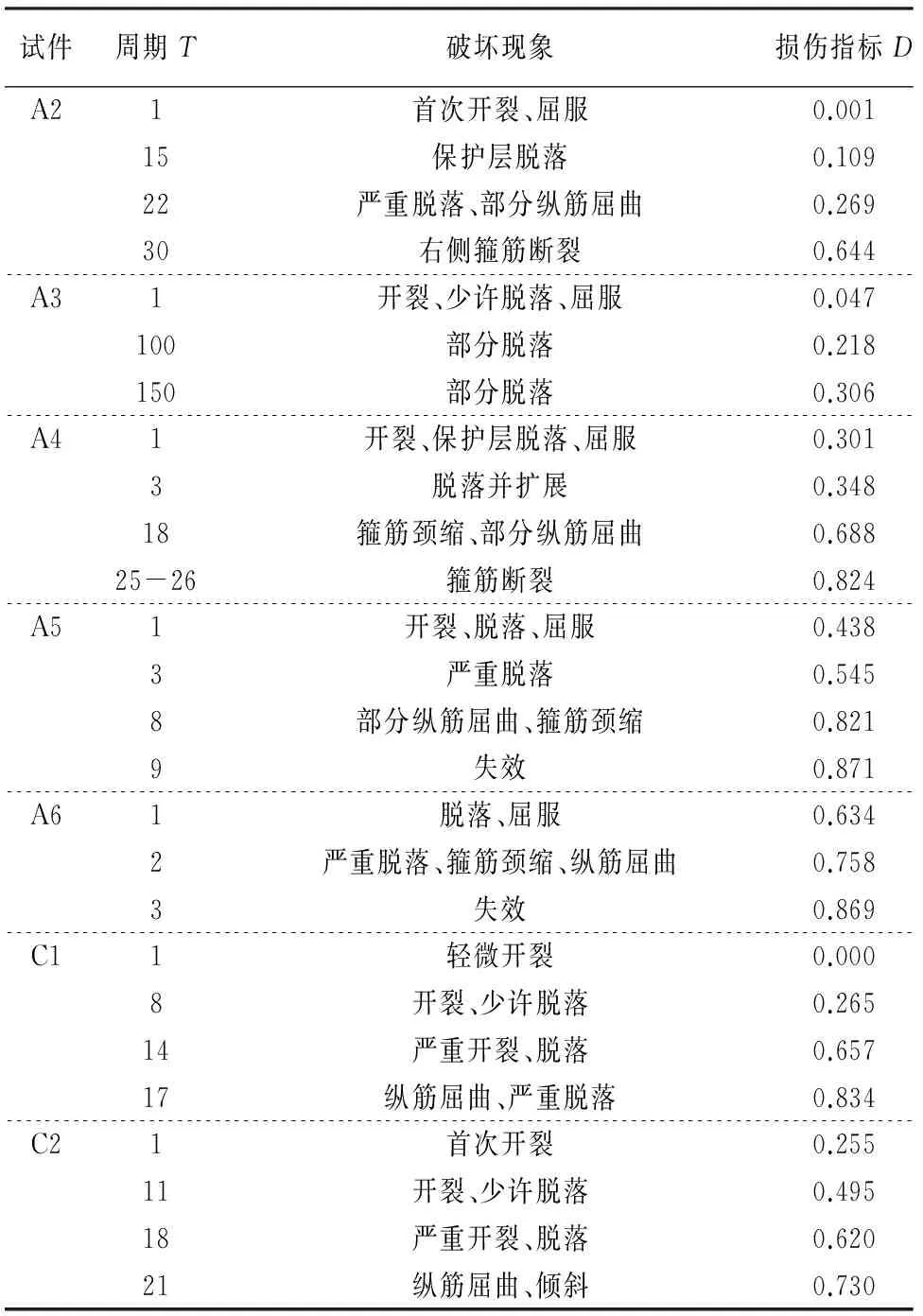
表4　试件的破坏现象及损伤指标Tab.4　Damage phenomenon and damage index of specimens

T(a) A2～A6试件

T(b) C1，C2试件图8　试件的损伤发展曲线Fig.8　Damage curve of specimens

通过图8及表3,表4，对比试验现象及相应的损伤指标，可以看出：

对于试件A2，损伤前期(第1周～第15周)，损伤增长缓慢，后期增长较快，该损伤模型能体现出试件在后期所经历的混凝土明显脱落、纵筋屈曲、箍筋断裂等损伤过程，但其损伤值偏小，试件失效时其损伤值仅为0.644，低估了试件的破坏程度，与试验现象不吻合；试件A3加载至150周时仅产生中等破坏，该模型能反映构件损伤发展缓慢的过程，但其损伤值偏小，低估了构件的破坏程度；对于试件A4～A6，损伤值与试验现象能大致吻合，根据该损伤模型总体上能判别试件的损伤状态.

对于试件C1，该损伤模型体现出试件在加载过程中随位移幅值增加而损伤加重的发展过程，能较好地反映构件的破坏情况；对于试件C2，该模型反映了试件在加载前期的损伤演化缓慢的现象，但稍微高估了试件的损伤程度，后期则稍微低估了构件的损伤.

通过以上分析可知：该损伤模型能较准确地反映首次超越破坏后，累积损伤的发展过程；其考虑了加载路径的影响，总体上判别试件损伤状态的准确性相对较高.

3　RC框架结构基于损伤的易损性分析

3．1钢筋混凝土框架结构设计

3.1．1结构基本信息

按照《建筑抗震设计规范》(GB 5001-2010)和《混凝土结构设计规范》(GB 50010—2010)，采用PKPM设计某五层三跨的钢筋混凝土框架结构办公楼，底层层高为4.2m，其他各层层高均为3.6m，结构总高度为18.6m，其平面布置图如图9所示.抗震设防烈度为8度(0.2 g)，环境类别为Ⅰ类，场地类别为Ⅱ类，设计地震分组为第二组.地表粗糙度为B类，基本雪压为0.5 kN/m2，基本风压为0.45 kN/m2.混凝土强度等级为C40，纵筋强度等级为HRB400，箍筋强度等级为HPB300.选取一榀框架进行分析，其立面布置图、配筋图如图10所示.

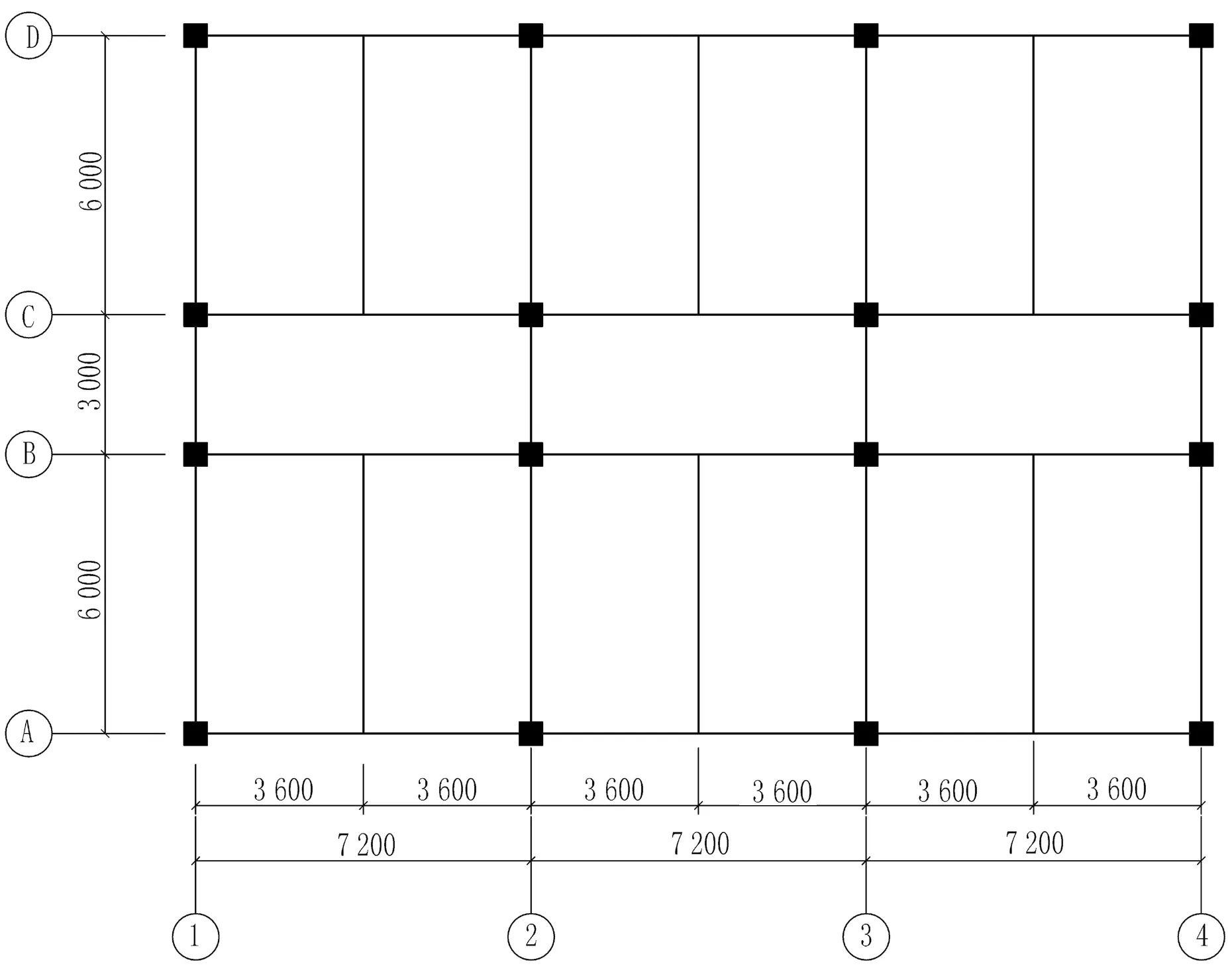
图9　框架结构平面布置图(mm)Fig.9　 Frame structural plan configuration(mm)

图10　框架立面布置图及构件配筋图(mm)Fig.10　Frame structural plan configuration and reinforcement assembly of components(mm)

3．1．2结构有限元模型

本文采用Opensees软件对该钢筋混凝土框架结构进行数值分析，结构有限元模型采用杆系模型，以梁、柱构件为基本单元，结构质量集中在节点上，质量根据重力荷载代表值(恒载+0.5活载)计算.本文采用纤维截面模型，梁、柱的截面纤维划分示意图如图11示.混凝土本构模型采用Concrete01模型，钢筋本构模型采用Steel02模型，在非线性动力分析中，各强度参数取其平均强度值，梁、柱构件的混凝土本构模型参数取值见表5.HRB400钢筋的强度平均值为463.61 MPa，钢筋的弹性模量为2.0×105MPa，钢筋从弹性阶段过渡至弹塑性阶段的控制参数取Opensees的建议值，即R0=18.5，cR1=0.93，cR2=0.15，钢筋的硬化率取0.01.梁、柱构件均采用基于力插值函数的非线性梁柱(Nonlinear Beam Column)单元模型，一根构件用一个单元来模拟.在进行动力时程分析时，采用瑞雷阻尼模型定义结构的阻尼矩阵.

(a) 柱截面

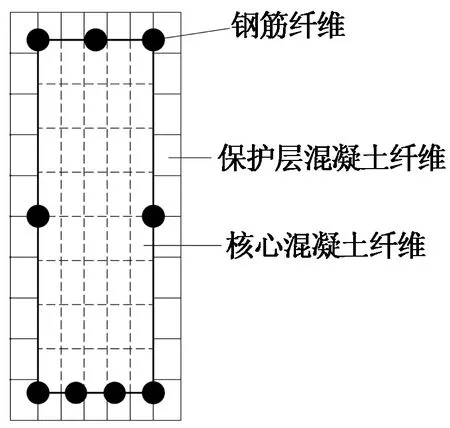
(b) 梁截面图11　框架结构各构件截面纤维划分示意图Fig.11　Fiber division diagram of component cross section in the frame structure表5　梁、柱构件混凝土本构模型的参数取值Tab.5　Parameter values in concrete constitutive model of beam and column

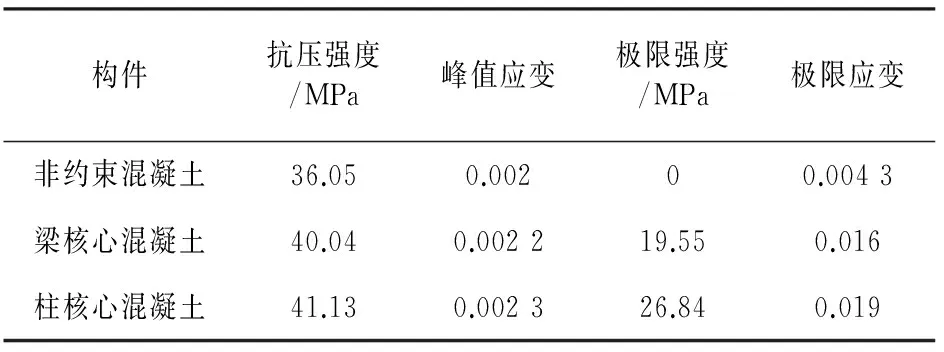
构件抗压强度/MPa峰值应变极限强度/MPa极限应变非约束混凝土36.050.00200.0043梁核心混凝土40.040.002219.550.016柱核心混凝土41.130.002326.840.019

结构有限元模型建立后，通过模态分析得到基本周期为0.955 s，与PKPM的结果0.949 s接近，表明框架结构有限元模型是比较准确与合理的.

3.2RC框架结构的损伤指标计算

对于钢筋混凝土框架结构，构件的损伤主要只集中在塑性铰区，因此，本文通过塑性铰区截面弯矩-曲率来计算截面的损伤指标，并采用最大损伤指标来表征构件的损伤.文献[7]研究表明该损伤模型的计算结果对β，γE和μo的取值不敏感.因此，对于梁、柱构件，本文统一取μ0=2.5，γE=0.1，β=0.1；梁、柱构件的屈服曲率与极限曲率通过对结构进行Pushover分析获得.

本文对结构进行Pushove分析时，采用倒三角加载方式，即水平荷载分布与结构各楼层的水平地震荷载分布一致.因该框架结构梁、柱构件分别统一配筋，对于梁构件，其截面屈服曲率与极限曲率均近似相同；对于柱构件，底层柱的轴压比较大，且地震是往复作用，底层各边柱之间、各中柱之间的轴压比均不同，为方便后续构件损伤指标的计算，区分为边柱、中柱：取各边柱的屈服曲率与极限曲率均与底层边柱的平均值相同，各中柱的屈服曲率与极限曲率均与底层中柱的平均值相同，这对于上层柱失效破坏时的损伤评估是偏安全的.

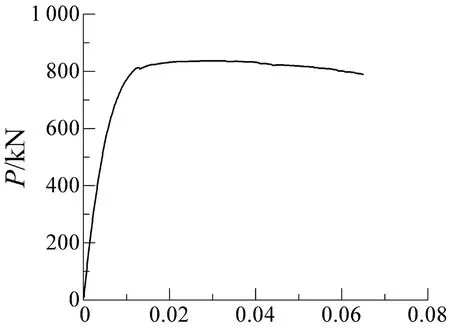
Pushover分析时，为使构件达到极限状态，取较大的控制位移(最大层间位移角达到6%)，结构基底剪力-最大层间位移角曲线(P-θmax)如图12所示，各构件截面的屈服弯矩、屈服曲率及极限曲率如表6所示.

θmax/rad图12　框架结构的Pushover曲线Fig.12　Pushover curve of the frame structure

3.3增量动力分析(IDA)

影响结构抗震性能的不确定因素主要包括地震

动的不确定性与结构本身的随机特性，相对于地震动的不确定性，结构的随机性对结构抗震性能的影响较小.对于中高层建筑结构，当选取相对合理有效的地震强度指标时，10～20条地震动记录通常能为结构的抗震性能评估提供足够的精度[9].选波长时综合考虑地震动的振幅、频谱特征与持时要求，地震动持续时间对结构的低周疲劳与累积破坏效应有重要的影响，一般要求包含地震动最强烈部分在内的地震动持时为结构基本周期的5～10倍且应大于10 s,同时近场地震动与远场地震动中的响应有所不同，为减小结构响应的离散性，美国ATC-63(2008)报告中通过震中距应大于10 km来区分近、远场地震动记录.

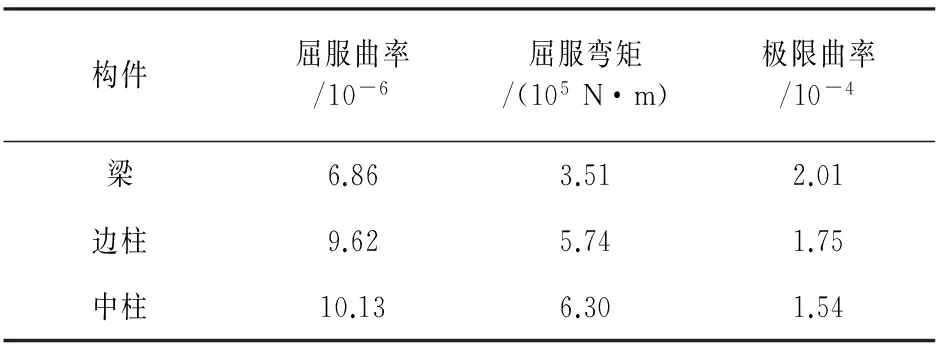
表6　梁、柱构件截面弯矩-曲率特征值Tab.6　Moment -curvature characteristic value of beam and column cross section

基于此，本文仅考虑地震动的随机性，根据框架结构的场地类别，在PEER Strong Motion Database 中选取18条满足震中距、持时等要求的地震波对结构进行IDA分析，为结构的地震易损性分析提供研究数据，具体数据如表7所示.各地震波的反应谱及均值反应谱如图13所示.

表7　18条地震波记录Tab．7　18 seismic records

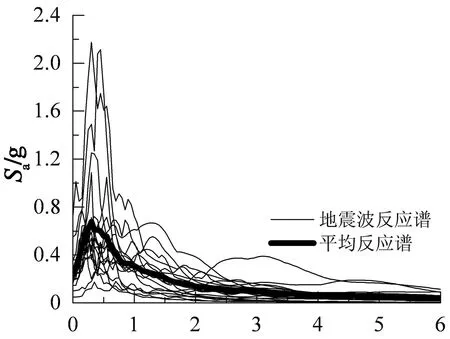
T/s图13　 各地震记录的反应谱Fig.13　Response spectrum of seismic records

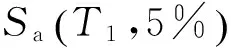
基于最大层间位移角θmax的设计方法是实现结构性能化设计的主要手段，θmax是运用比较广泛地地震需求参数.因此，本文分别选取基于构件层次的结构损伤指数DE，θmax作为地震需求参数，通过对比分析来探讨结构基于损伤的抗震性能评估方法的可行性.

《建筑抗震设计规范》(GB 0011-2010)划分出结构的5个性能状态并给出了相应的最大层间位移角θmax参考值，本文结合规范参考值及文献[11]，[12]等中的研究成果，确定出各性能状态的θmax限值.各性能状态下不同地震需求参数的取值范围如表8所示.

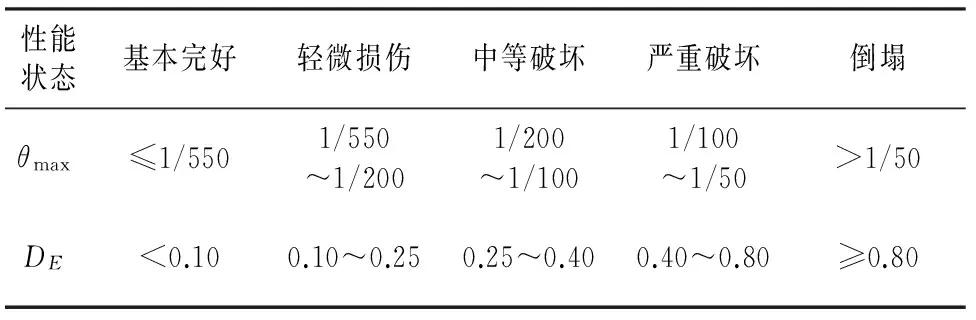
表8　各地震需求参数在不同性能状态下取值范围Tab．8　Value range of seismic demand parameters in different performance states

在Opensees中可直接得到结构的层间位移角响应值，为了减少计算量以及在基于不同地震需求参数的IDA曲线上体现出各个性能点，本文取IDA分析的极限状态为结构达到动态不稳定、非线性时程分析不收敛的点或θmax达到10%与相应IDA曲线中20%的初始斜率所对应的地震强度较小点.此外，地震强度过大并无实际意义，本文取Sa(T1,5%)的最大值为2.5 gIDA分析时首次取Sa(T1,5%)=0.05g，此后以0.1 g为增量，依次在[0.1 g,2.5 g] 区间取值.

1)基于构件损伤的IDA结果

采用构件塑性铰区截面弯矩-曲率计算整个结构的损伤指标DE，可得到相应的IDA曲线(DE-Sa(T1,5%)).以1#地震记录为例，其IDA曲线如图14所示.

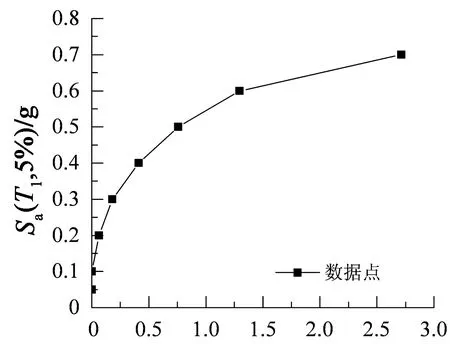
DE图14　1#地震波的IDA曲线Fig.14　IDA curve of 1# seismic record

从图14可以看出：当Sa(T1,5%)较小时，结构损伤指数约为0，表明结构处于基本完好状态；随着Sa(T1,5%)的增加，IDA曲线逐渐变得平缓，表明结构破坏程度逐步加深；最后结构的损伤指数远远大于0.8，表明结构已经倒塌失效.

根据表8，结构的各性能点如图15所示，当DE=0.8，Sa(T1,5%)=0.508g时，结构达到倒塌破坏的临界点，此后，损伤指标随地震强度快速增长，能较好地表征结构的失效状态.

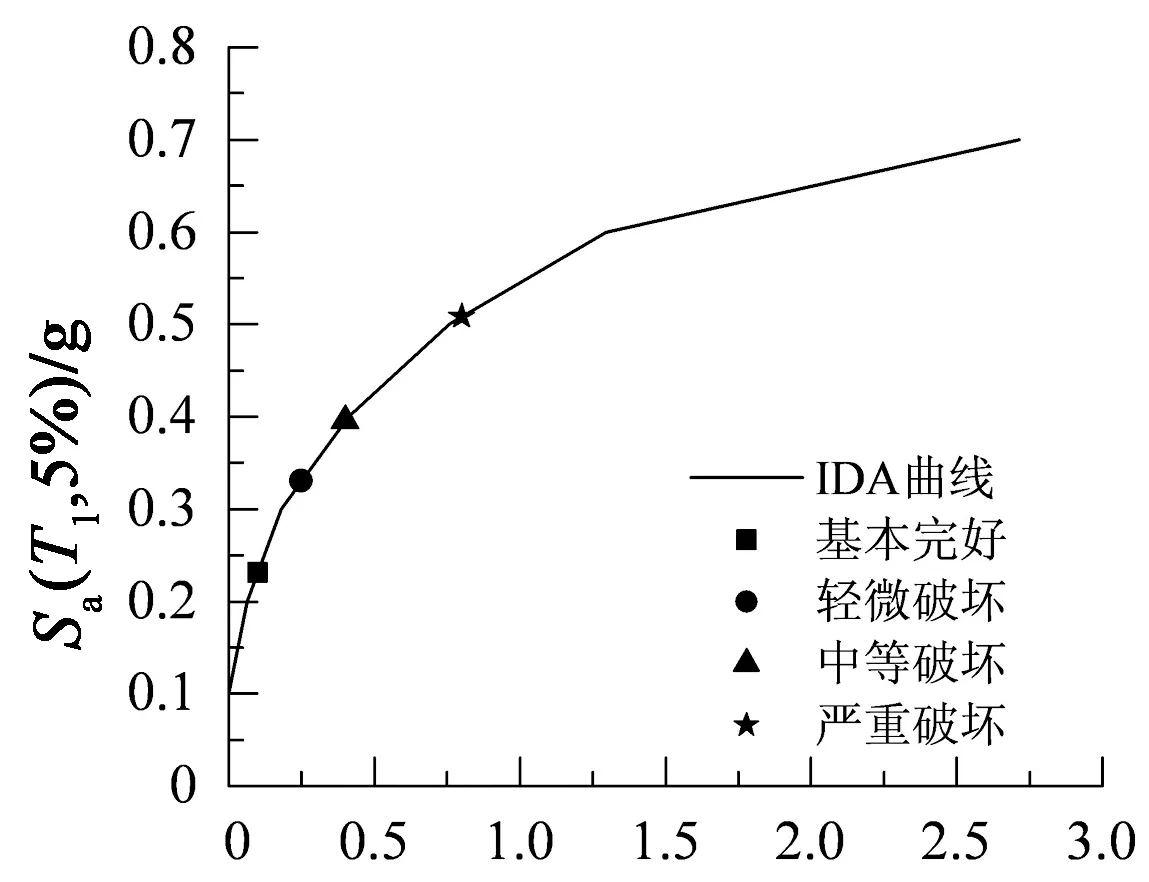
DE图15　1#地震波 IDA曲线的性能点Fig.5　 Performance point on the IDA curve of 1# seismic record

1#地震记录调幅至不同强度时，结构构件塑性铰区截面的损伤发展及各楼层的损伤(DET)分布情况分别如图16,17所示.由图16，17可知：随着地震强度的增加，结构、楼层、构件的损伤逐步发展；楼层损伤由下至上逐渐减小，底层为结构的薄弱层，其损伤发展较快，柱底破坏严重，Sa(T1,5%)=0.6g时，柱底截面全部失效破坏；结构破坏时未产生理想的“梁铰机制”，而是“梁柱混合机制”；梁柱节点处，未完全实现“强柱弱梁”的设计原则.

注：未标注符号的构件表示其处于基本完好状态图16　结构的损伤发展过程Fig.16　 Damage development process of the structure

DET图17　结构各楼层损伤指标随地震强度的变化Fig.17　 Damage index variation along with the change of seismic intensity of the structural storeys

多条地震记录基于构件损伤的IDA曲线(DE-Sa(T1,5%))如图18所示．不同地震记录下的IDA曲线与1#地震波的IDA曲线发展规律相似，随着地震强度的增加，IDA曲线逐渐变得平缓；结构达到IDA分析的极限状态时，其损伤值远大于其倒塌破坏性能点的限值0.8，结构已经失效破坏.

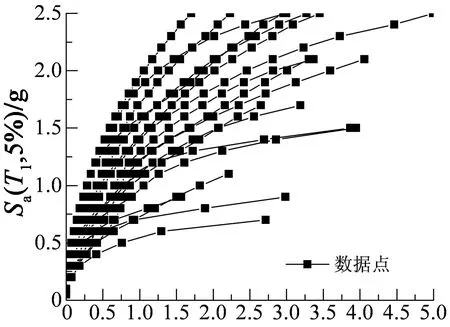
DE图18　18条地震波的IDA曲线Fig.18　IDA curve of 18 seismic records

2)基于最大层间位移角的IDA结果

根据结构的层间位移角响应，可得到基于最大层间位移角的IDA曲线(θmax-Sa(T1,5%)).以1#地震记录为例，其IDA曲线如图19所示.

从图19可以看出：当Sa(T1,5%)较小时，IDA曲线初始阶段近似呈线性增长，表明结构处于弹性状态；随着Sa(T1,5%)的增加，曲线斜率逐渐减小，表明结构处于弹塑性发展状态；最后曲线变得平缓，地震强度仅稍微增大，结构产生较大的变形，表明结构处于倒塌破坏状态；IDA曲线较好地反映出结构由完好至破坏的发展过程.

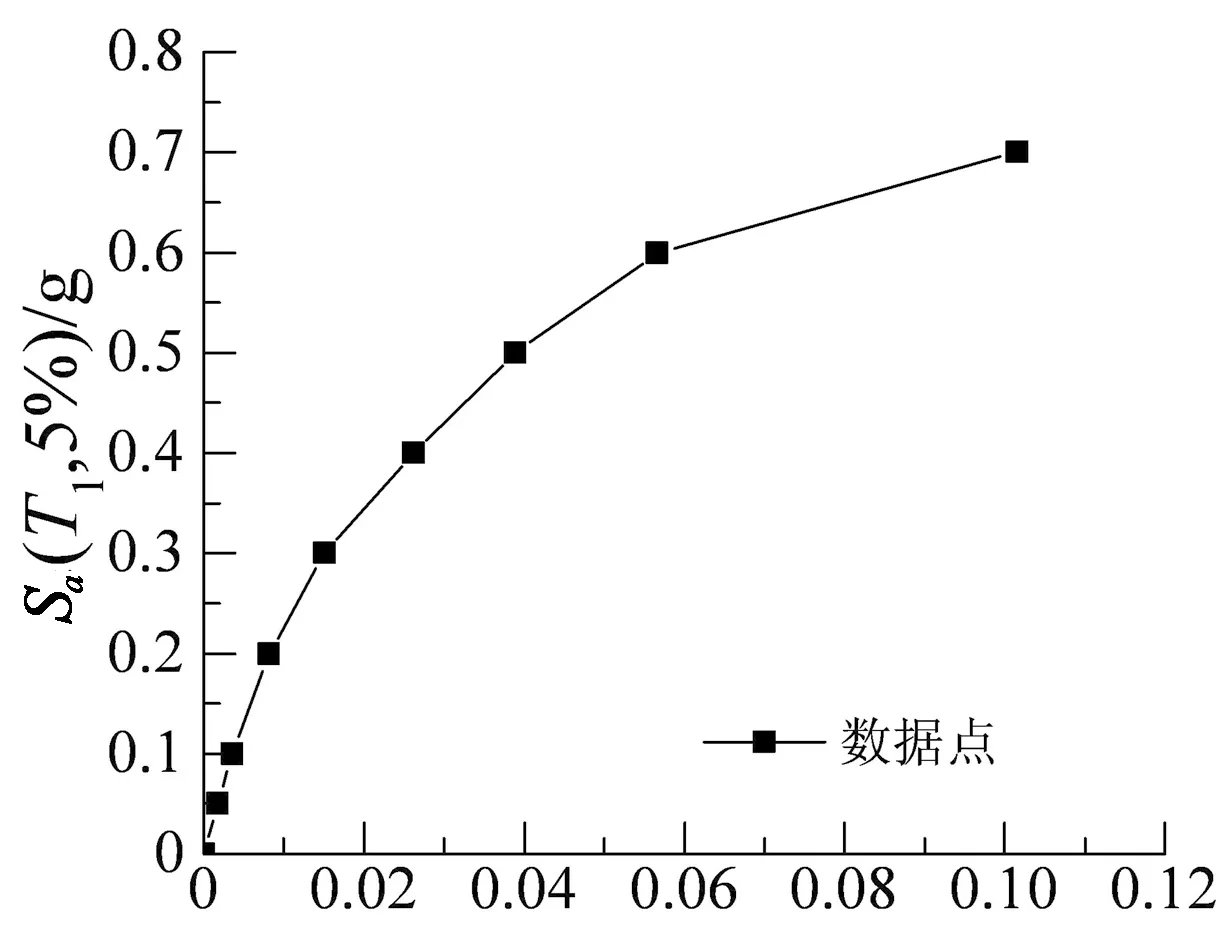
θmax/rad图19　1#地震波的IDA曲线Fig.19　IDA curve of 1# seismic record

根据表8，在θmax-Sa(T1,5%)曲线上定义各个性能点，如图20所示，当θmax=1/50，Sa(T1,5%)=0.349g时，结构达到严重破坏状态的极限点，这比前文定义的IDA分析的极限状态点要保守很多，此时IDA曲线仍具有较大斜率，结构还可承受更大的地震强度.

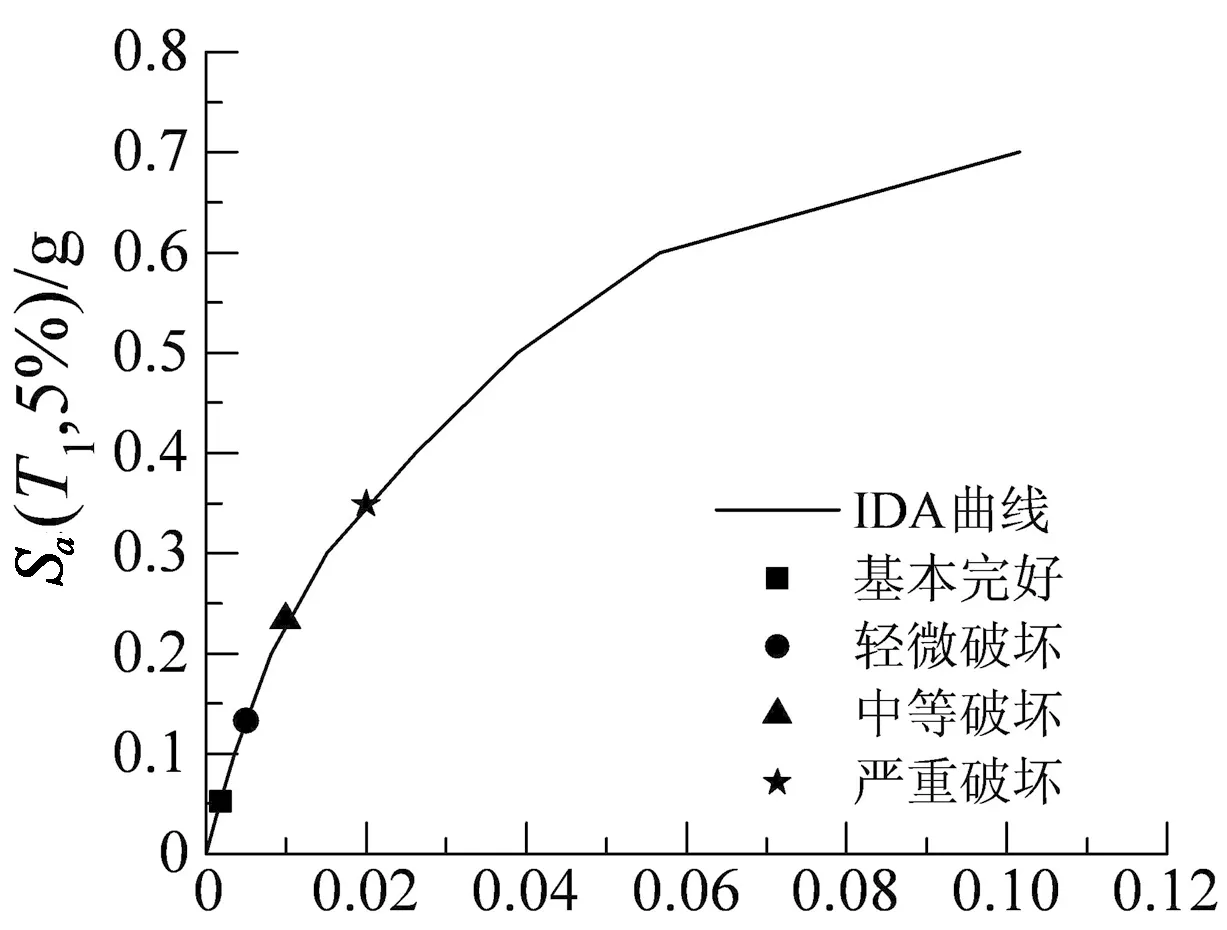
θmax/rad图20　 1#地震波IDA曲线的性能点Fig.20　Performance point on the IDA curve of 1# seismic record

1#地震波调幅至不同强度时，结构层间最大位移角的分布情况如图21所示，结构各层最大层间位移角均随着地震强度的增大而增大；层间变形随着楼层增加而减小，在不同地震强度下的最大层间位移角均发生在第1层，第1层为该结构的薄弱层.

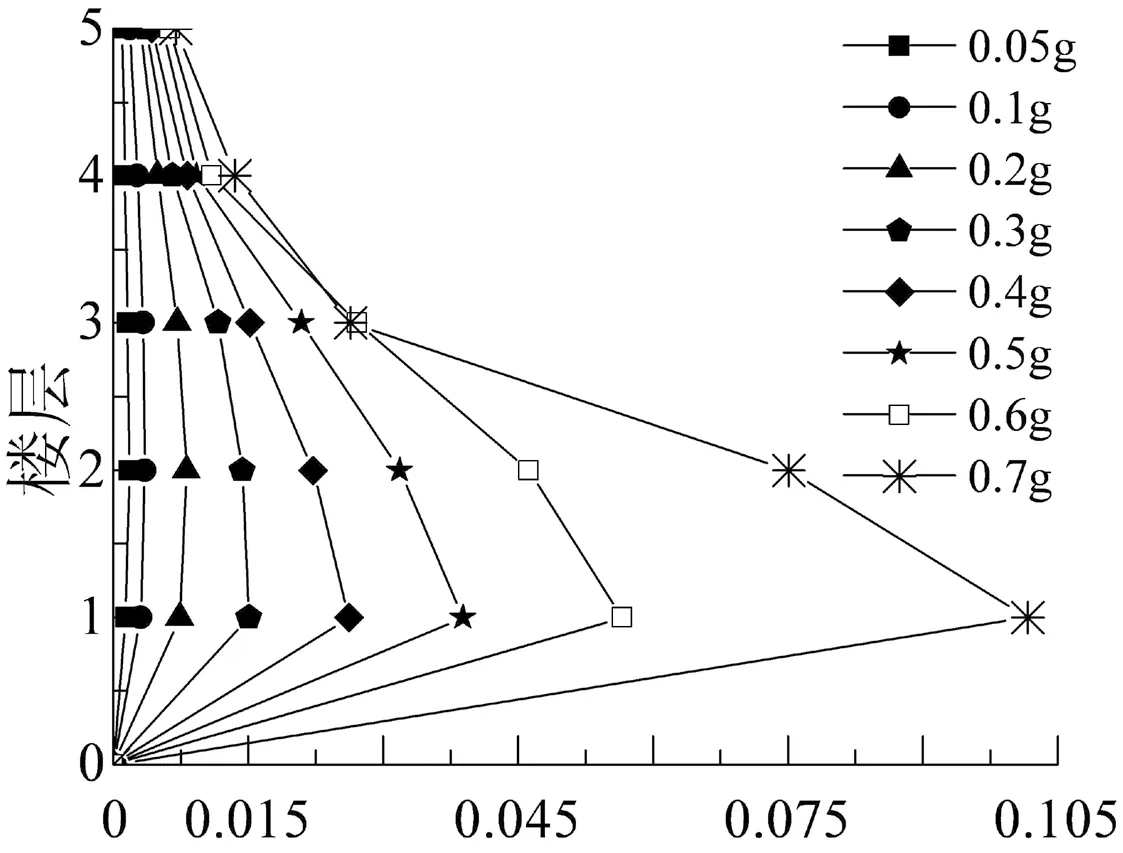
θmax/rad图21　结构各层最大层间位移角随地震强度的变化Fig.21　The maximum inter-story drift ratio variation

多条地震记录基于最大层间位移角的 IDA曲线(θmax-Sa(T1,5%))如图22所示，当结构达到表8中倒塌破坏的性能点，即θmax=1/50时，结构仍具有较大的承载力与变形能力.

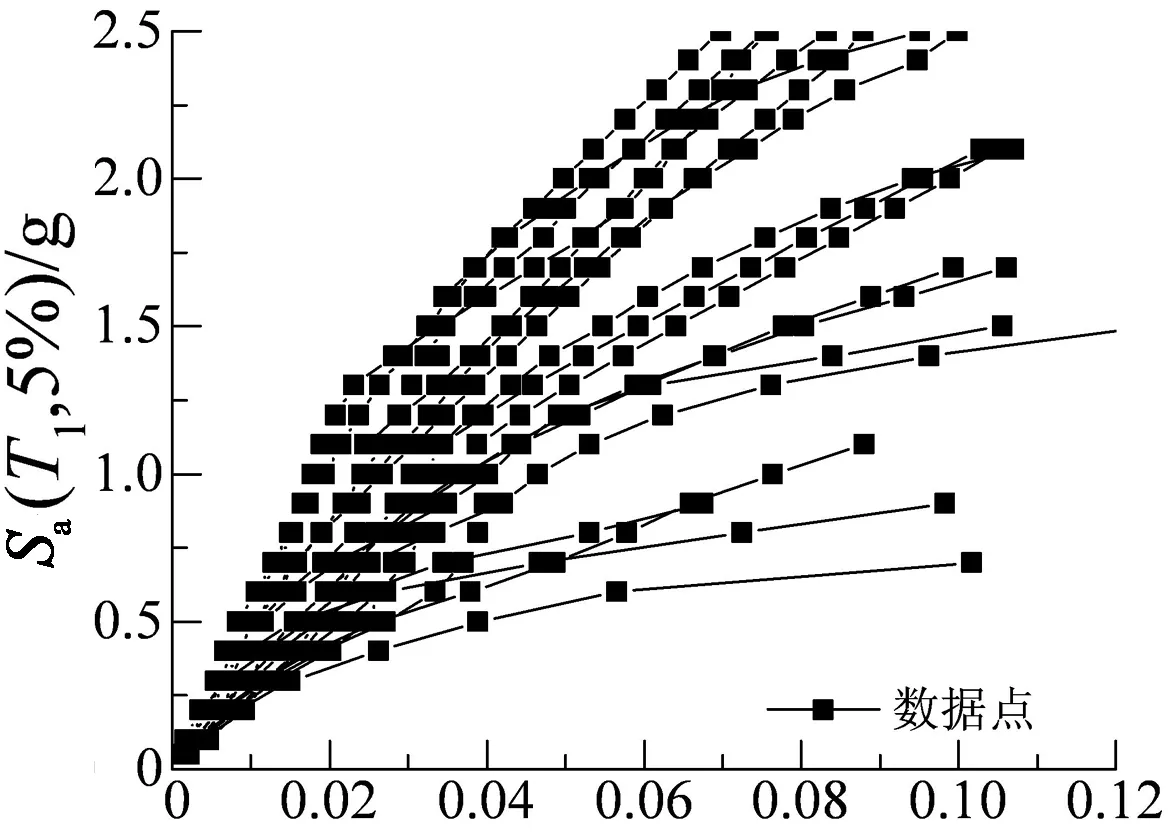
θmax/rad图22　18条地震波的IDA曲线Fig.22　IDA curve of 18 seismic records along with the change of seismic intensity of the structural storeys

对比基于不同地震需求参数的IDA分析结果可知：

1)基于结构损伤指标的IDA曲线与基于最大层间位移角的IDA曲线发展规律相似，基于损伤指标的IDA分析能较好地反映结构构件、楼层、整体结构的损伤发展过程、结构的失效破坏机制，能判别结构的薄弱构件与楼层，从而可以把握结构的局部薄弱环节，为结构抗震设计与分析提供参考依据．基于结构最大层间位移角的IDA分析不能反映结构局部构件的损伤情况，仅能粗略地判断结构的薄弱层；

2)在同一地震记录同一强度下，基于不同地震需求参数所判别的结构性能状态可能不同，且结构损伤指标会产生超出1.0的情况，不能很好地体现损伤指标原始定义的基本含义，参考规范给出的最大层间位移角倒塌性能点限值偏保守.

3．4RC框架结构的地震易损性分析

3.4．1地震易损性分析模型

结构的地震易损性分析是指在不同强度地震作用下结构的地震需求超过某一性能状态或某一确定限值C的条件概率.文献[13]中的研究表明，地震强度IM与结构需求参数ID之间满足如下关系：

(3)

其对数表达式为：

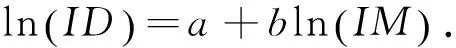
(4)

式中：α，a，b为回归系数.

结构的地震概率需求函数可用对数正态分布函数表示，即

(5)

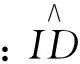
(6)

其对数形式为：

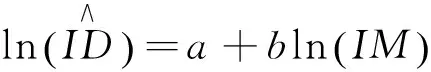
(7)

(8)

(9)

3．4．2基于构件损伤的地震易损性分析

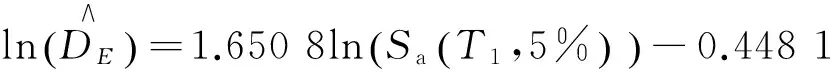
βDE=0.530 2 ．

(10)

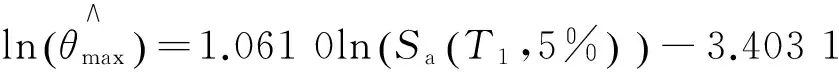
βθmax=0.367 9．

(11)

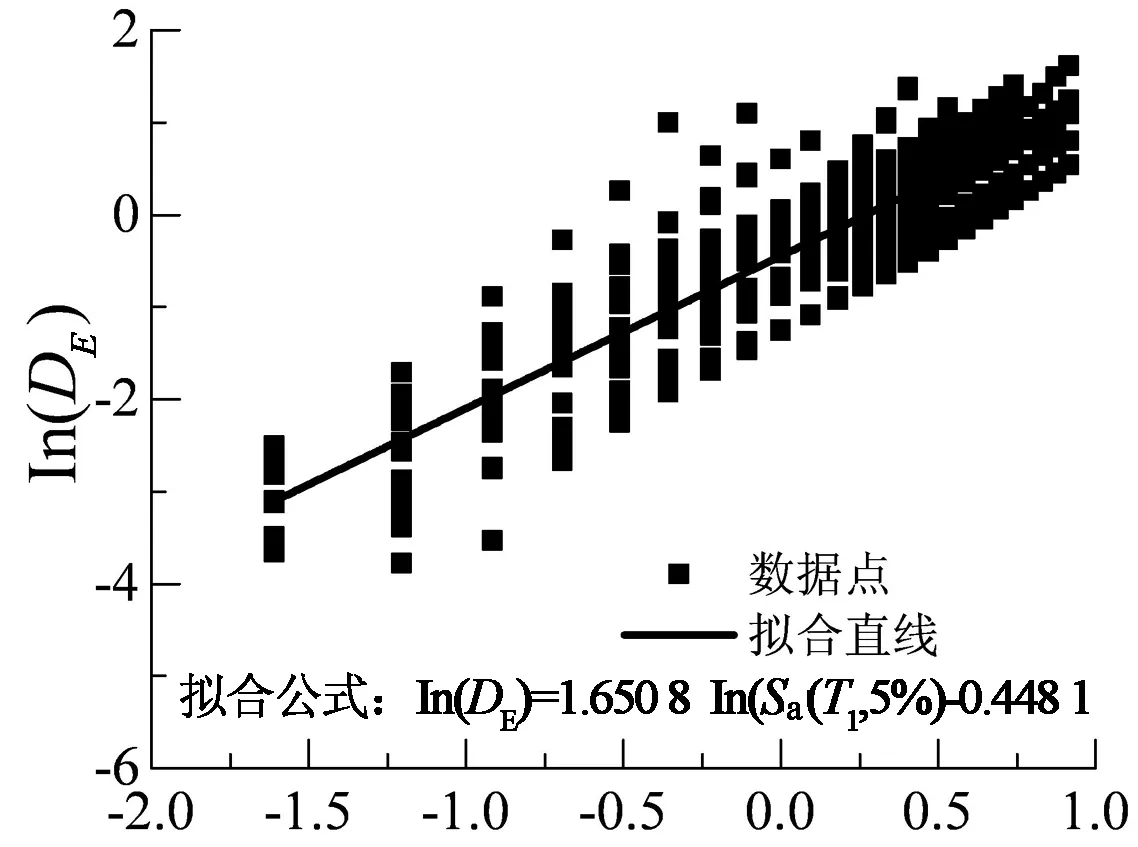
ln(Sa(T1,5%)) (a) 计算模型ln(PGA)-ln(Sa)回归曲线

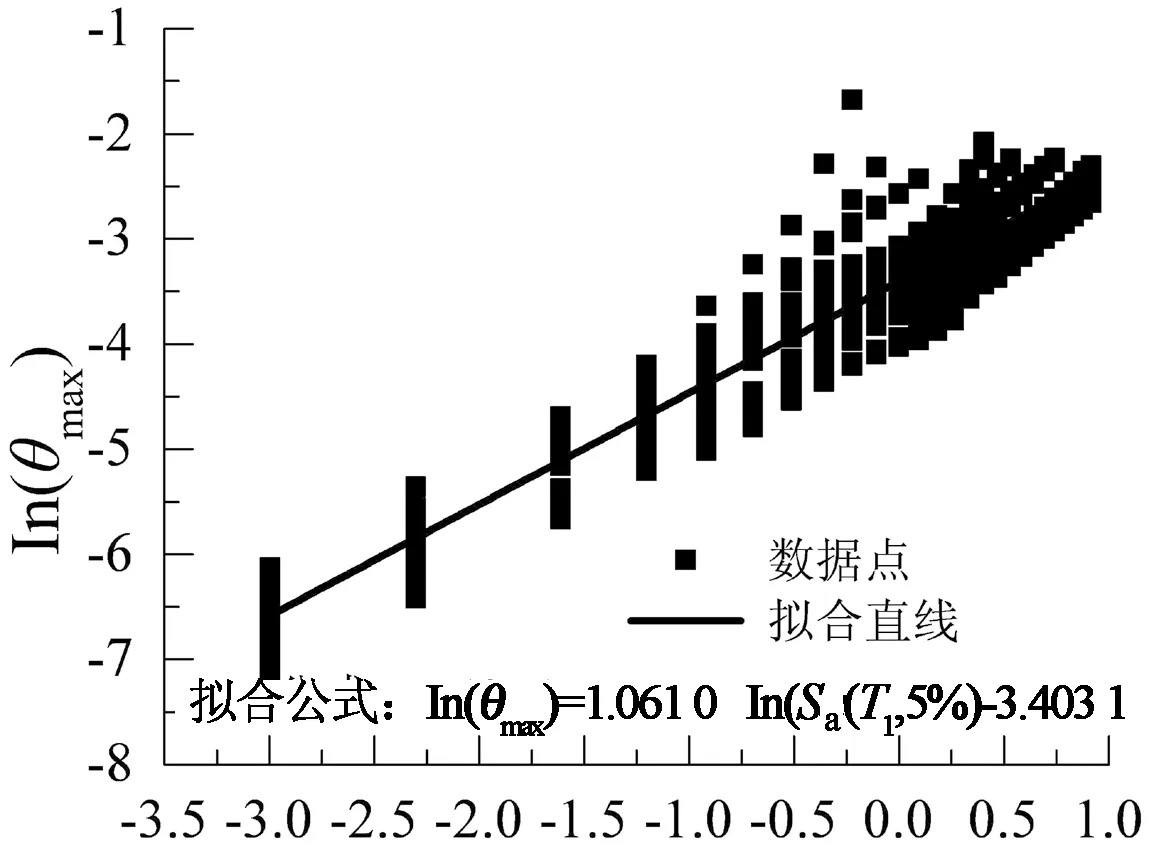
ln(Sa(T1,5%)) (b) 计算模型ln(θmax-ln(Sa)回归曲线图23　结构概率地震需求模型Fig.23　Probabilistic seismic demand model of the structure

根据表8中各个性能状态下DE,θmax的取值范围，由式(9)可得结构超越各性能水平的概率：

(12)

(13)

相应的结构地震易损性曲线如图24，25所示.

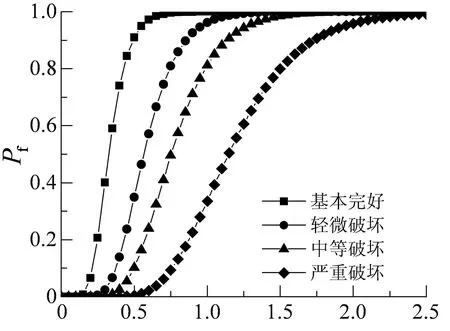
Sa(T1,5%)/g图24　结构基于损伤的易损性曲线Fig.24　Structural fragility curve based on damage

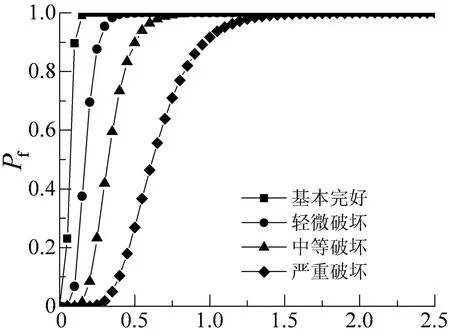
Sa(T1,5%)/g图25　结构基于最大层间位移角的易损性曲线Fig.25　Structural fragility curve based on the maximum inter-story drift ratio

由基于不同地震需求参数的结构易损性分析结果可以看出：

1) 各地震记录对应的ln(Sa(T1,5%)) -ln(DE),ln(Sa(T1,5%))-ln(θmax)近似呈线性关系，较好地满足线性要求.

2) 基于损伤指标的易损性曲线与基于最大层间位移角的易损性曲线发展规律相似，其能评估结构在不同地震强度下各性能状态的失效概率；结构由基本完好发展至倒塌性能状态，基于损伤的易损性曲线逐渐变得平缓，相同地震强度下，其失效概率逐渐减小，曲线发展趋势与结构设计原则相吻合.

3．4．3地震易损性分析结果的对比研究

在上述易损性分析的基础上，对比各性能状态下基于不同地震需求参数的分析结果，如图26所示.

Sa(T1,5%)/g (a)基本完好的超越概率

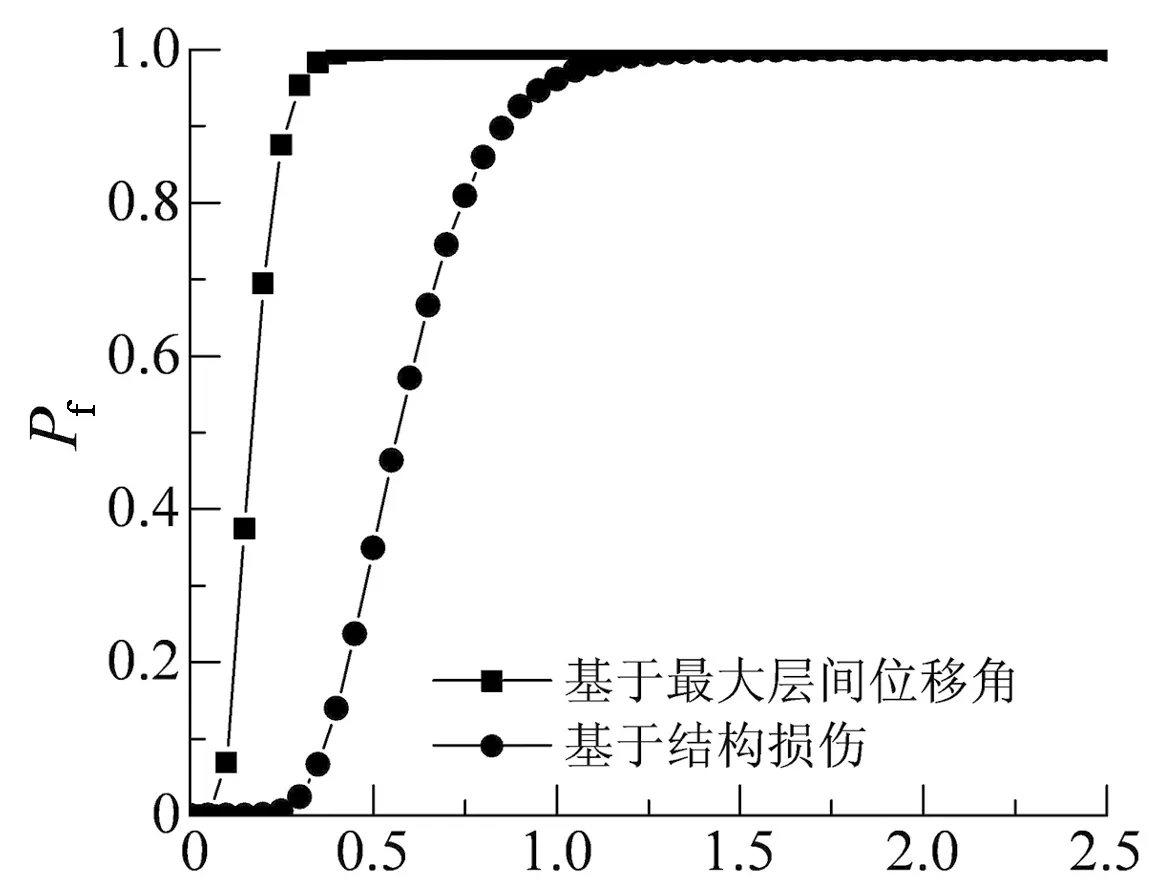
Sa(T1,5%)/g (b)轻微破坏的超越概率

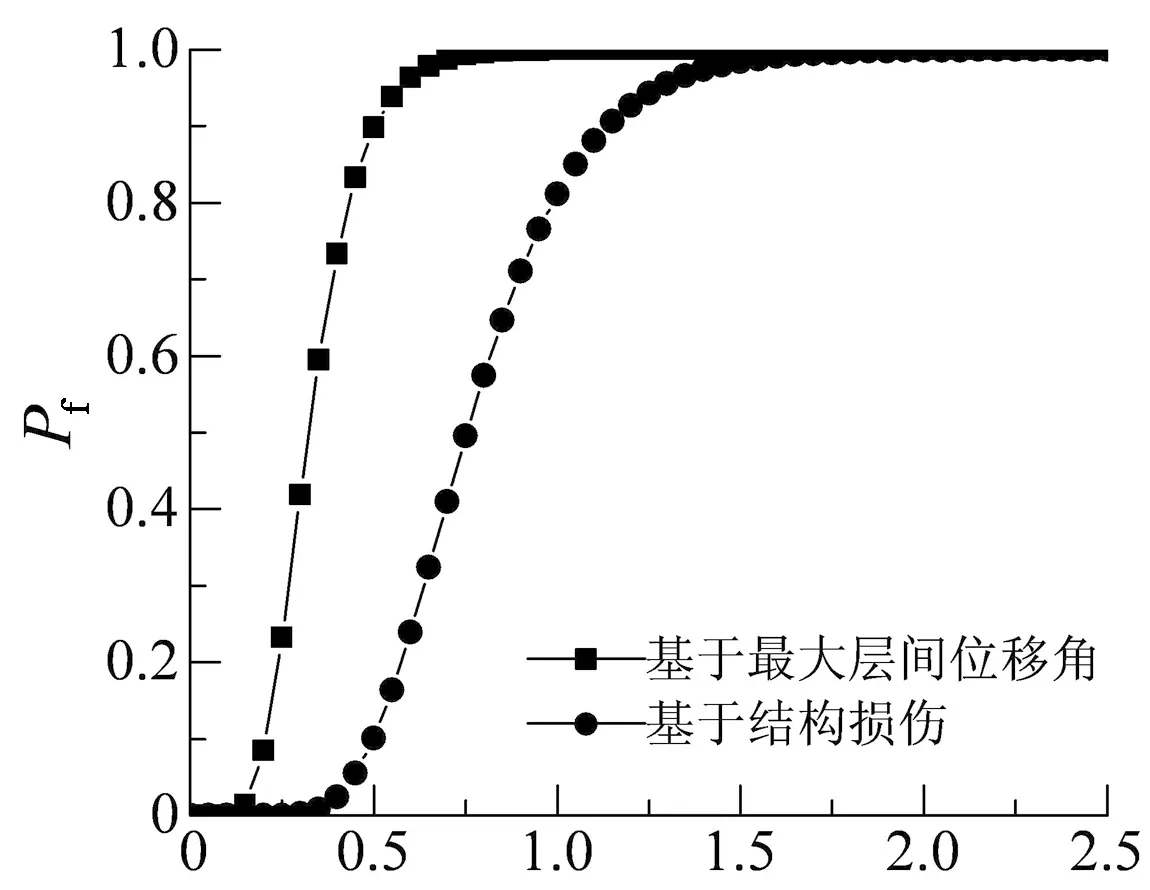
Sa(T1,5%)/g (c)中等破坏的超越概率

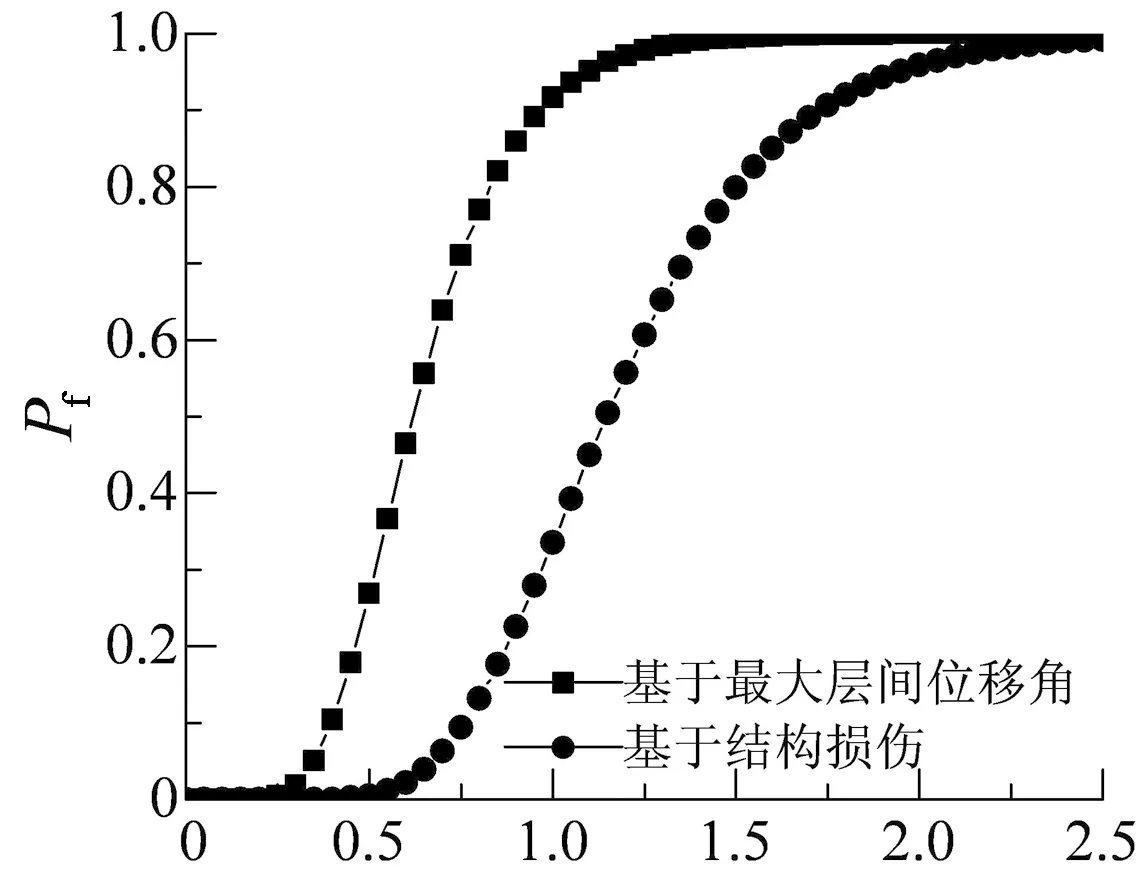
Sa(T1,5%)/g (d)严重破坏的超越概率图26　 结构的超越概率曲线Fig.26　Failure probability curve of the structure

由图26可知：

1)地震强度较小时，结构近似完好或损伤程度较小，在不同性能状态下基于不同地震需求参数的易损性曲线基本重合；地震强度较大时，结构弹塑性变形充分发展，在同一性能状态下，结构基于不同地震需求参数的超越概率不同.

2)地震强度较大时，在不同性能状态下，各易损性曲线均表现出结构基于最大层间位移角的超越概率较大，结构在较小地震强度下倒塌概率已达到100%，基于结构最大层间位移角的抗震性能评估结果偏保守，结构在倒塌性能状态下仍有较强的承载能力与变形能力，结构是偏安全的；基于结构损伤的易损性分析结果则充分考虑了构件的耗能能力与非线性变形能力，结构在较大地震强度下才能达到倒塌性能点.

3) 基于结构变形的单一性能指标难以经济而合理地评估结构的抗震性能，基于结构损伤的抗震性能评估方法综合考虑了结构的响应与自身的能力，更全面的评估了结构的性能，具有良好的可行性.

4　结　论

1)王东升提出的修正Park-Ang模型考虑了加载路径的影响，能较准确地反映首次超越破坏后，累积损伤的发展过程，且总体上判别试件损伤状态的准确性相对较高.

2)基于结构损伤指标的IDA曲线与基于最大层间位移角的IDA曲线发展规律相似，基于结构损伤的IDA能较好地反映构件、楼层、整体结构的损伤发展过程及结构的失效破坏机制，能准确地判别结构在地震下的局部薄弱环节，为结构抗震设计与分析提供依据，但结构损伤指标会出现超出1.0的情况，不能很好地体现损伤指标原始定义的基本含义.

3)基于结构最大层间位移角的抗震性能评估结果偏保守，难以全面、准确地评估结构的抗震性能；基于结构损伤的抗震性能评估方法综合考虑了结构的响应与自身的能力，更全面地评估了结构的性能水准，能预测结构在不同地震强度下各性能状态的失效概率，其具有良好的可行性.

[1]KUNNATH S K, REINHOM A M, PARK Y J. Analytical modeling of inelastic seismic response of R/C structures[J]. Journal of Structural Engineering, 1990, 116(4): 996-1017.

[2]KUMAR S, USAMI T. Damage evaluation in steel box columns by cyclic loading tests[J]. Journal of Structural Engineering, 1996, 122(6): 626-634.

[3]CHAI Y H, ROMSTAD K M, BIRD S M. Energy-based linear damage model for high-intensity seismic loading[J]. Journal of Structural Engineering，1995,121(5): 857-864.

[4]欧进萍,牛荻涛,王光远. 多层非线性抗震钢结构的模糊动力可靠性分析与设计[J]. 地震工程与工程振动,1990, 10(4): 27-37.

OU Jin-ping, NIU Di-tao, WANG Guang-yuan． Fuzzy dynamical reliability analysis and design of multi-storey nonlinear aseismic steel structures[J]．Earthquake Engineering and Engineering Vibration,1990，10(4): 27 -37.(In Chiaese)

[5]牛荻涛,任利杰. 改进的钢筋混凝土结构双参数地震破坏模型[J]. 地震工程与工程振动,1996, 16(4): 44-54.

NIU Di-tao, REN Li-jie. A modified seismic damage model with double variables for reinforced concrete structures [J]. Earthquake Engineering and Engineering Vibration, 1996, 16(4): 44-54. (In Chiaese)

[6]吕大刚,王光远. 基于损伤性能的抗震结构最优设防水准的决策方法[J]. 土木工程学报,2001, 34(1): 44-49.

LV Dag-ang, WANG Guang-yuan. Decision- making method of optimal fortification level for aseismic structures based ondamage performance[J]．China Civil Engineering Journal，2001，34( 1) : 44-49.(In Chiaese)

[7]王东升,冯启民,王国新. 考虑低周疲劳寿命的改进Park-Ang地震损伤模型[J]. 土木工程学报，2004, 37(11): 41-49.

WANG Dong-sheng, FENG Qi-min, WANG Guo-xin. A modified Park-Ang seismic damage model considering low-cycle fatigue life [J]. China Civil Engineering Journal, 2004, 37(11): 41-49. (In Chiaese)

[8]KUNNATH S K, El-BAHY A, TAYLOR A W,etal. Cumulative seismic damage of reinforced concrete bridge piers[R]. Technical Report NCEER, US National Center for Earthquake Engineering Research, Buffalo, 1997-0006.

[9]陈昉健，易伟建. 近场地震作用下锈蚀钢筋混凝土桥墩的IDA分析[J]. 湖南大学学报:自然科学版, 2015，42(3):1-8．

CHEN Fang-jian, YE Wei-jian. Incremental dynamic analysis of corroded reinforced concrete bridge columns subjected to near-field earthquake [J]. Journal of Hunan University :Natural Sciences, 2015，42(3):1-8.(In Chiaese)

[10]-叶列平,马千里,缪志伟. 结构抗震分析用地震动强度指标的研究[J]. 地震工程与工程振动,2009,29(4): 9-22.

YE Lie-ping，MA Qian-li，MIAO Zhi-wei． Study on earthquake intensities for seismic analysis of structures[J]．Earthquake Engineering and Engineering Vibration，2009，29,(4): 9-22. (In Chiaese)

[11]靳鑫.基于地震动参数的钢筋混凝土结构易损性分析[D].太原：太原理工大学建筑与土木工程学院,2011:47-79．

JIN Xin. The vulnerability analysis of the reinforced concrete structure based on the ground motion parameters[D]. Taiyuan:College of Architecture and Civil Engineering, Taiyuan University of Technology, 2011:47-79.(In Chiaese)

[12]黄悠越. 基于构件性能的RC框架结构层间位移角性能指标限值研究[D].广州：华南理工大学土木与交通学院,2012: 47-64．

HUANG You-yue. Research on the story drift limits of RC frame structures based on the components performance [D]. Guangzhou：School of Civil Engineering and Transportation, South China University of Technology,2012: 47-64.(In Chiaese)

[13]龚思礼.建筑结构设计系列手册-建筑抗震设计手册[M].2版.北京:中国建筑工业出版社,2003：175-187.

GONG Si-li. Building structure design series manual- building seismic design manual [M]. 2nd ed. Beijing: China Building Industry Press, 2003:175-187.(In Chiaese)

Research on Seismic Performance Assessment Based on Component Damage for RC Frame Structure

ZHANG Yao-ting1†, DU Xiao-ju1,2, YANG Li1

(1．Huazhong Univ of Science and Technology,School of Civil Engineering and Mechanics, Wuhan,Hubei430074, China; 2．Chengdu JZFZ Architecture Design Co Ltd, Chengdu,Sichuan610021，China)

This paper study discussed the applicability of Park-Ang model modified by Wang based on the pseudo-static test results of reinforced concrete columns. The structural damage index based on the component level was selected, and both the incremental dynamic analysis and fragility analysis of the reinforced concrete frame were conducted. Additionally, the prediction by the modified method to evaluate the seismic performance in terms of the damage index of the RC frame was compared with the maximum inter-story drift ratio of the fragility analysis result. The analysis results show that the modified Park-Ang model that considers the loading path effect predicts well the cumulative damage process after the first damage, which discriminates the specimen damage status accurately, the damage development process, and the overall and local failure mechanism. Further, the weak links can be accurately distinguished. However, the damage index higher than 1.0 may be caused by using these methods, which cannot accurately reflect the basic meaning of the original definition. Compared with the maximum inter-story drift ratio, the seismic performance evaluation method using the damage index considers the structural response and properties. The modified method can be used to evaluate the structural performance more comprehensively and predict the failure probability of the structures under different earthquake loads.

reinforced concrete frame; fixed Park-Ang damage model; incremental dynamic analysis; fragility analysis; pseudo-static test of columns

2015-07-03

国家自然科学基金资助项目(51278218),National Natural Science Foundation of China(51278218)

张耀庭(1965-)，男，湖北红安人，华中科技大学教授†通讯联系人，E-mail:zyt1965@mail.hust.edu

1674-2974(2016)05-0009-13

TU375

A