基于随机响应的电力系统虚拟建模方法研究
2016-08-24王桢祎刘多伦
王桢祎 刘多伦 佟 欣
(1. 东北电力大学 2. 华北电力大学)
基于随机响应的电力系统虚拟建模方法研究
王桢祎1刘多伦1佟欣2
(1. 东北电力大学2. 华北电力大学)
电力系统建模是电力系统仿真计算的基础,恰当的系统模型能正确反映系统运行情况,便于在线分析和操作。电力系统的不断发展使其愈加庞大复杂,能源结构的多样化和负荷模型的复杂化使电力系统随机因素进一步增加,随机因素对整个系统都产生不可忽视的影响。所以基于随机因素产生的响应信号准确辨识系统状态空间模型,对实际电力系统的分析和控制至关重要。本文提出一种基于系统随机响应信号辨识其状态空间模型的子空间辨识法。由于建模目的是用于设计振荡阻尼控制器,所以,此辨识方法的输入数据应采集系统可控点信号,输出数据采集能反映系统主导振荡模式的信号。以三机9节点系统为例,采用子空间辨识法能在较短时间内辨识出系统降阶状态空间模型,并与系统全阶状态空间模型进行时域和频域对比,分析结果表明该辨识模型能反映系统的动态特性,可以用于设计振荡阻尼控制器。
随机响应;状态空间;系统辨识;子空间辨识法
0 引言
电力系统建模是电力系统仿真计算的基础[1]。恰当的系统模型能够与实际系统良好对应,便于在线分析电力系统运行情况,进而合理安排调度,提高传输能力,消除安全隐患,具有显著的经济和社会效益[1]。如果模型不够准确,会使得仿真结果与实际不符,不能正确处理或预见系统中发生的问题,造成不可估量的人力、物力损失。随着我国电力系统的发展,各地电力电量交换活跃,区域优化配置资源成效显著,目前全国已实现六大电网互联、2014年APEC会议中提出中国与周边国家实现联网,电源结构进一步优化,水电、核电、气电、清洁煤发电和新能源发电等清洁电力比重争取超过35%。这使得电力系统变得愈加庞大复杂,随机因素进一步增加。
现阶段考虑系统随机因素影响的电力系统建模思想主要有两类:一类是直接在确定性模型的基础上引入刻画系统随机扰动的随机变量,用以研究电力系统的随机动态过程以及稳定性[2-3],该方法良好辨识系统局部模型,对于辨识整个系统差强人意。另一类是在系统中引入类噪声信号,充分分析在此噪声环境下电力系统运行情况及特点,完成无附加激励下的电力系统模型辨识,该方法采用Prony法、递推最小二乘法、子空间辨识法等先进的数学方法建立系统模型。
本文提出一种针对第二类建模思想的数学方法,考虑利用子空间辨识法辨识电力系统状态空间模型,从输入输出角度出发,规避了传统随机系统辨识中以随机微分方程为基础辨识系统模型所带来的一系列复杂问题。以往的基于子空间辨识法辨识电力系统状态空间模型都是通过设置短路故障或者冲击负荷辨识系统振荡模式,根据所查找的国内外文献,研究由在系统上设置持续存在的高斯白噪声来辨识出的状态空间模型并不多见,所以研究是十分必要的。
1 理论基础
1.1子空间辨识法
子空间辨识法是一种只根据系统输入输出,无需确切知道系统的内部结构和参数的确定线性时不变系统状态空间模型的方法之一,尤其针对高阶系统。用现场辨识测试进行动态建模,可自然计及运行中的一些实际因素;适用于一些物理机理尚不清楚或难以用简单规律描述的动态过程[1]。在系统建模中具有以下特点:①不需要参数化;②不需要参数迭代优化,运算速度快;③模型阶数可以在辨识过程中得到;④采用的数值计算工具简单,如QR分解、SVD等;⑤直接估计状态空间模型,适宜于多变量系统辨识[6]。该算法原理和思路文献[8]中已全部给出,不再赘述。
虽然电力系统是一高度非线性系统,但如果电力系统处于“小偏离”状态,即输入的随机激励在很小的范围内变化时,系统仍然是稳定的,在该稳态点对电力系统模型的非线性方程进行Taylor展开,忽略高次项的影响,这时电力系统模型可表示为线性时不变模型。这样就可用上述子空间法辨识电力系统状态空间模型。
1.2模型输入输出的选取
模型输入输出数据的选择也有一定要求。理论上,电力系统中任何位置的测量信号都可以反映系统的振荡模式都能用于辨识系统状态空间模型。然而在本课题中,基于子空间辨识法获得模型的目的是对系统进行振荡阻尼控制,所以应选择系统中实际可控的信号作为辨识方法的输入信号,例如:电力系统稳定器(PSS)、FACTs器件、HVDC线路等的可控点信号。换句话说,子空间辨识法的输入信号应可以通过控制调节抑制目标振荡模式。而子空间辨识法的输出信号应能反映系统的主导振荡模式,通常采用可以反映系统振荡的观察信号,例如转子角速度、传输线有功功率和发电机母线频率。本研究输入信号选择自动电压调节器(AVR)的励磁电压Uf,输出信号选择发电机相对功角δ[7]。
1.3验证方法的选择
采用两个角度验证模型,即:
1)时域角度验证。给定相同的输入信号分别注入到原系统和辨识出的系统模型中,分别得到相应的输出信号,将得到的时域输出对比看它们是否拟合良好。对于原系统和辨识出的系统,输入信号均为所有自动电压调节器(AVR)的励磁电压,输出信号均为所有发电机的角速度,它们物理上一一对应。理论上两系统相对应的输出应良好拟合。
2)频域角度验证。系统的频率特性能反映出系统对不同频率的输入信号的跟踪能力,且只与系统的结构与参数有关,是线性系统的固有特性。在电力系统仿真软件PSAT中建立电力系统状态空间模型是全阶模型,而采用子空间辨识法得到的系统状态空间模型是降阶模型,显然它们的特征值不能一一对应,但是每一个特征值都能反映系统的某一固有特性。将两系统的特征值进行对比,若都能对应系统某一低频振荡模式,则辨识是有效的。
2 基于随机响应的电力系统虚拟建模方法流程分析
本研究课题是基于随机响应的电力系统虚拟建模,在MATLAB中进行仿真研究。计划研究步骤如下:
1)采用电力系统分析软件(PSAT),基于实际电力系统模型得出负荷高斯白噪声作用下,系统全阶状态空间模型;
2)对同样的实际电力系统模型注入同样的高斯白噪声,采集合适位置的随机响应,作为子空间辨识法的输入和输出;
3)采用子空间辨识法(N4SID)基于上述数据,得出电力系统降阶状态空间模型;
4)对得到的两个状态空间模型进行时域和频域分析判断辨识结果的可靠性;
5)基于模型准确性分析结果,研究该辨识方法及辨识过程中存在的问题并提出改进措施。
3 子空间辨识算法有效性分析
以四阶系统为例,其数学表达式如下

对此二输入二输出系统输入高斯白噪声序列U=[U1U2](N=1000,T=0.01),采集系统输出y=[y1y2]采用子空间辨识法辨识系统的状态空间模型,将两模型进行时域和频域角度分析。
1)时域角度验证。图1是系统输入的两随机高斯白噪声信号,图2是在相同的随机信号输入下,原系统和辨识系统输出时域比较,其中y1拟合于原系统97.07%,y2拟合于原系统96.6%,说明拟合效果非常好。
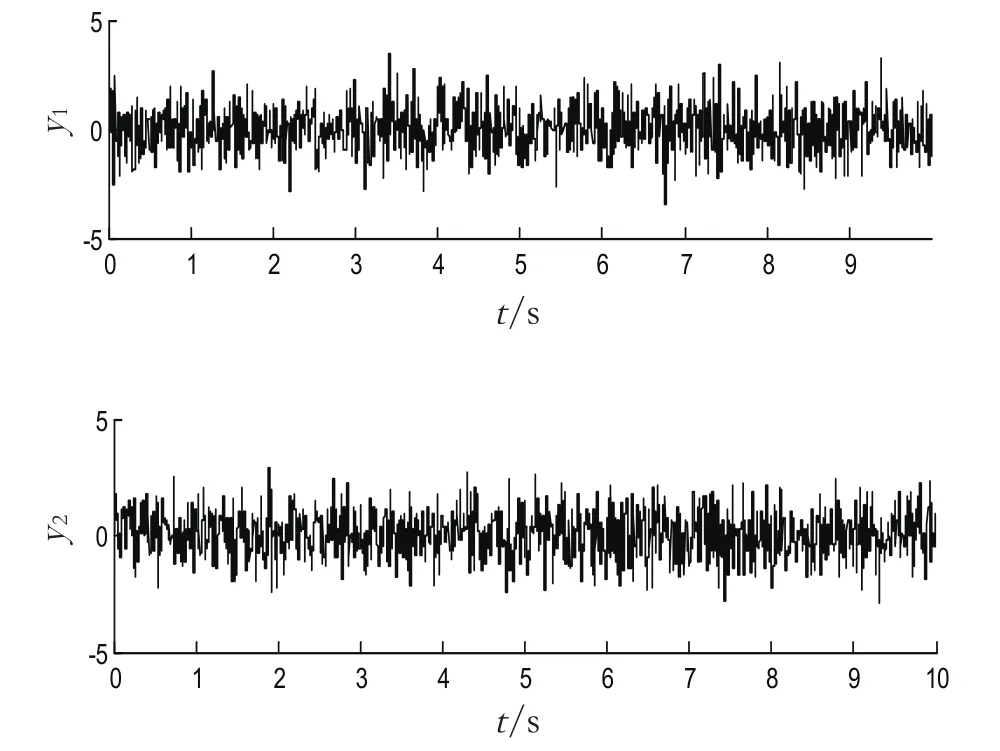
图1 系统二高斯白噪声输入
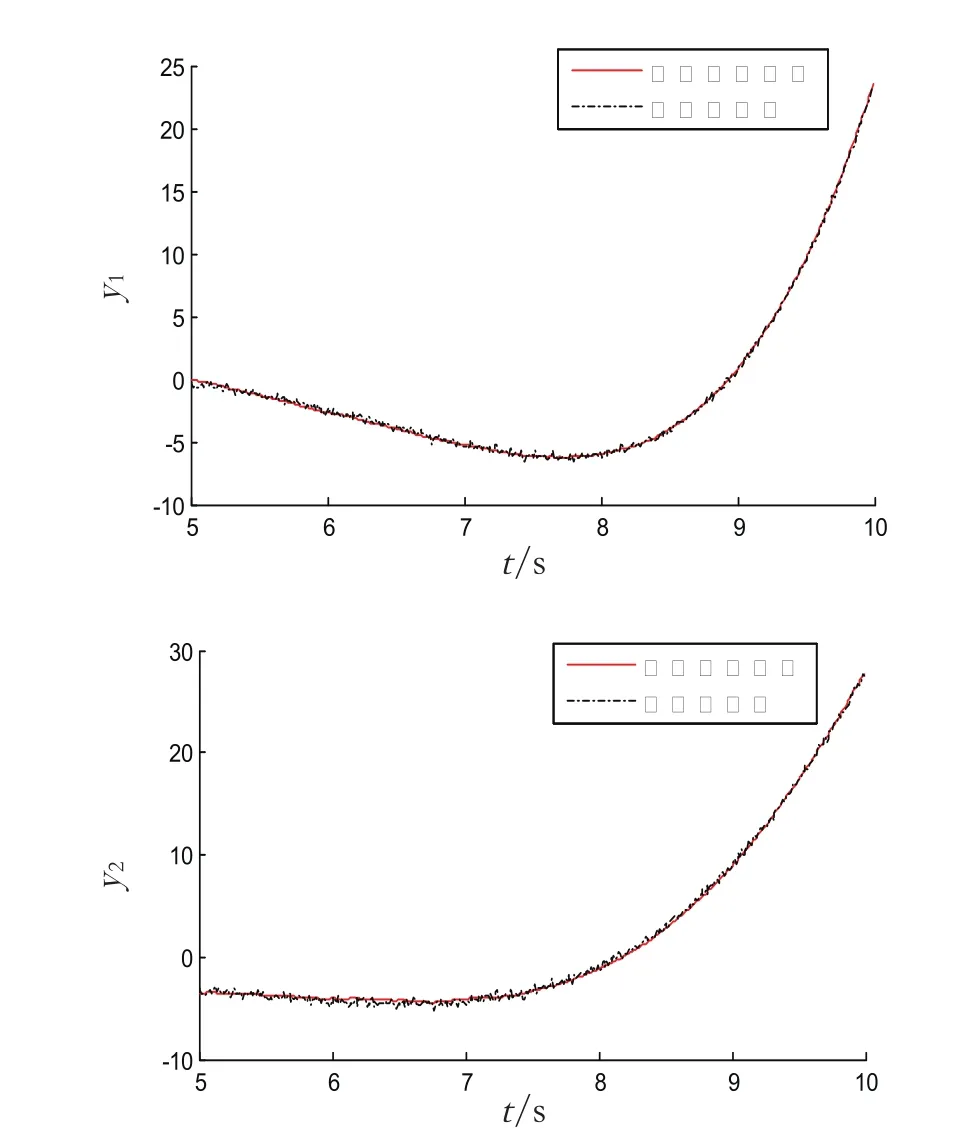
图2 原系统与辨识系统输出时域验证对比图
2)频域角度验证。表1是原系统特征值与辨识系统特征值对比,可以看辨识出的系统特征值与原系统十分接近,证明子空间辨识法能反应原系统的动态特性。

表1 原系统与辨识系统特征值对比图
4 多机系统仿真分析
以三机9节点系统为例,辨识其状态空间模型。三机9节点算例单线图如图3所示,数据参见PSAT说明书。

图3 三机9节点系统单线图
对此系统进行小干扰稳定分析得出其特征值及所有低频振荡模式,并求出各振荡模式的频率和阻尼比,如表2所示。可以看出系统存在两个频率分别为1.2147Hz 和1.8472Hz的本地振荡模式,分别对应发电机G2和G3,而发电机G1为平衡机,所以采集三台发电机励磁电压Uf作为子空间辨识法的输入信号,发电机G2和G3与参考机G1的相对功角δ12和δ13作为子空间辨识法的输出信号能够辨识出系统的所有主导振荡模式。

表2 小干扰稳定分析结果
首先,将系统存在的所有随机性因素近似看成是具有平稳独立增量的零均值高斯过程,将其作用于电力系统仿真软件PSAT中的电力系统模型中所有负荷处,其波动范围为负荷的5%,得出系统的全阶状态空间模型;然后,采集自动电压调整器(AVR)的励磁电压Uf的时域仿真信号作为子空间辨识法的输入,采集相对功角δ12和δ13的时域仿真信号作为子空间辨识法的输出,采用子空间辨识法辨识出二输入三输出的系统状态空间模型,得到A、B、C、D各矩阵,对信号进行奇异值分解得到模型阶数为5。
1)时域角度验证。对原三机9节点系统和辨识系统三个励磁电压Uf处输入相同激励信号进行时域仿真,采集两系统输出的相对功角δ12和δ13信号,将两组输出进行时域对比,取11~21s的信号,可以看出在相同的激励下,δ12拟合于原系统88.81%,δ13拟合于原系统85.49%,说明原系统和辨识系统时域特性十分接近。
2)频域角度验证。求出辨识系统特征值及所有振荡模式,并求出各振荡模式的频率和阻尼比,如表3所示。

表3 子空间辨识法分析结果
对比表2和表3可知,在负荷处注入5%随机波动的扰动负荷,子空间辨识法能够辨识出系统的全部低频振荡模式。
5 结束语
1)本文采用了子空间辨识法,基于电力系统中随机因素产生的响应信号辨识了系统降阶状态空间模型,此模型能够反映系统的动态特性,可以获得系统低频振荡模式,可以根据辨识模式设计振荡阻尼控制器。
2)与其他方法相比,子空间辨识算法仅基于输入输出数据,不需要迭代优化,仅依靠简单的线性算法,实现容易。
3)本文仅是基于随机响应对系统虚拟建模的初步探索,证明基于电力系统随机响应能够辨识出系统状态空间模型,此模型能反映系统的动态特性。本文采集了励磁电压和发电机相对功角作为子空间辨识法的输入输出信号,可以辨识出系统的两个主导低频振荡模式,但是并没有采集其他能反映系统振荡模式的信号(如发电机角速度、母线电压、联络线功率等 ),还需进一步探索。
4)三机9节点系统相较于实际系统过小,下一步要以New England测试系统为研究对象,进一步基于随机响应辨识其状态空间模型,并且获得其低频振荡模式,进而设计震荡阻尼控制器。
[1] 鞠平,张建勇.电力系统基本理论研究综述[J].电力科学与技术学报,2011,26(1):4-12.
[2] 彭云建,邓飞其.电力系统随机稳定性分析与控制问题综述[J].电工电能新技术,2007,26(3):52-58.
[3] 彭云建,程培,邓飞其.随机非线性动态系统数值模拟与性态分析[J].控制理论与应用,2011,28(8):1126-1132.
[4] 索江镭,胡志坚,刘宇凯,等.基于多新息耦合最小二乘算法的电力系统状态空间辨识[J].电力自动化设备,2015,35(7):65-73.
[5] 刘咏飞,鞠平,薛禹胜,等.随机激励下电力系统特性的计算分析[J].电力系统自动化,2014,38(9):137-142.
[6] 李幼凤,苏宏业,褚健.子空间模型辨识方法综述[J].化工学报,2006,57(3):473-479.
[7] 蔡国伟,杨德友,张俊丰,等.基于实测信号的电力系统低频振荡模态辨识[J].电网技术,2011,35(1):59-65.
[8]倪以信,陈寿孙,张宝霖.动态电力系统的理论和分析[M].北京:清华大学出版社,2002.5.
(2016-03-02)
