基于小波阈值去噪的过电压信号处理

李　舜　李　雍　甘　粲

（西华大学电气与电子信息学院）

基于小波阈值去噪的过电压信号处理

李舜李雍甘粲

（西华大学电气与电子信息学院）

过电压是导致电力系统故障的主要原因，现场设备采集到的过电压中含有大量故障信息的特征量，对于分析故障发生原因至关重要，但受到现场环境的影响，采集到的实际波形都会混入大量高斯白噪声，严重干扰工作人员对事故原因的判断。因此消除过电压中对分类识别有干扰影响的噪声部分很有必要。本文基于小波阈值去噪的方法，在考虑传统软、硬阈值缺陷的基础上构造了新的阈值函数，对仿真及实测的过电压波形进行去噪处理和分析，并与传统的软、硬阈值去噪法进行了对比，验证了本方法的正确性和优越性。研究结果可以为电力系统在线监测处理过电压数据，分析故障原因奠定基础。

小波阈值去噪；阈值函数；过电压信号

0　引言

过电压是导致电力系统故障的主要原因，现场设备采集到的过电压中含有大量故障信息的特征量，对于分析故障发生原因有关键作用，但受到现场环境的影响，采集到的实际波形都会混入大量高斯白噪声，为了提高监控设备采集波形的准确性，同时为事故原因分析做好准备，需要进行消噪处理［1-3］，除去与信号特征量无关的成分。

由Donoho提出的基于小波的阈值去噪法由于其实用性，在工程中应用广泛，并得到了良好的检验［2］。阈值去噪法传统采用的阈值函数为软、硬阈值函数，软阈值函数在小波域内连续，但大于阈值的小波系数经软阈值处理后，会与原系数存在恒定偏差，这会使部分高频信息损失。硬阈值函数相较于软阈值函数而言，虽然没有恒定偏差，但在小波域内的 λ和 −λ处存在间断点［4-5］。

本文在充分考虑软、硬阈值函数缺陷的基础上，构造了一种新的阈值函数，利用小波阈值去噪法，在有效保留过电压信号特征量的同时去除过电压信号中的噪声分量，为后续对过电压数据的识别、分析和处理奠定坚实的基础。

1　小波变换

1.1小波变换及去噪原理

实际的采集过程中，信号都是以离散的形式存储起来的。需要经过小波离散变换得到其小波系数［6］

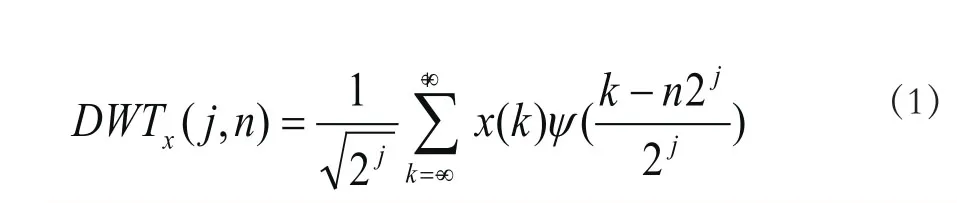
通过S.Mallat提出的多分辨分析，将信号分解成逼近分量和细节分量在第j层分解尺度下的逼近系数Cj（n）和细节系数dj（n）分别

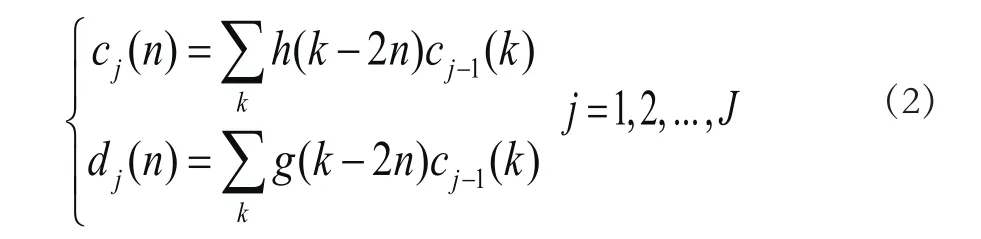
小波阈值去噪主要由三个步骤组成，首先进行离散小波变换，在对获得的小波系数进行阈值量化处理，最终反变换得到过电压信号，流程图如图1所示。

图1　信号去噪流程图

其中，离散小波变换的母小波选择，多分辨率分解层数确定，阈值函数的优劣和阈值估计方法的选择这几个方面直接决定了对过电压信号的去噪效果。

“此次堰塞湖的溃坝的具体时间难以预测，而往年金沙江汛期洪水是可以根据上游来水是可以根据上游来水进行提前判断和测量的。”云南电网公司生技部主任姚婕说，此次洪峰事发突然，难以预测，而且传播的能量更大、速度更快、破坏力更强，要想跑赢洪峰，就不能打无准备的仗。

1.2评价系 数

对过电压消噪要求去除噪声的同时而保留过电压信号中包含的对故障分析起关键作用的特征量，但这在实际中是很难达到的。因此本文引入文献［7］定义的两类信噪比SNR和SNR*以及评估系数η，在保证原始信号丢失最少的情况下，对过电压信号消噪效果进行评估。

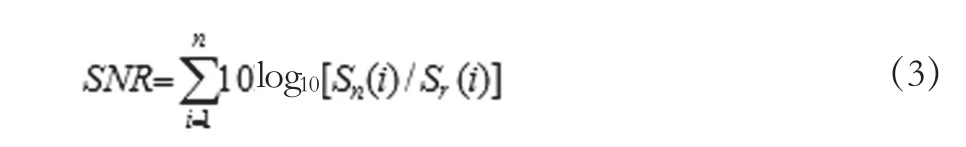
式中，Sn为含噪声的过电压信号，Sr为去噪后过电压信号中的残余噪声，由式（3）可知，信噪比越大，说明去噪效果越好，以此参数来衡量噪声去除程度。

式中，So为不含噪声的过电压信号，Sl为去噪过后丢失的信号，由式（4）可知，信噪比越大，说明还原效果越好，以此参数来衡量信号特征量保留程度。

构造评估系数η作为评判标准［7］，定义为

η越小，表明去噪的效果越不理想。

1.3小波层数确定

多分辨分析分解层数直接决定了在消噪过程中，处理过电压信号的灵活度。根据唯一变量原则，在阈值函数，母小波和阈值规则相同的条件下，对加入白噪声的不同过电压波形进行处理，表1为得到在不同分解层数下SNR和SNR*以及评估系数η。

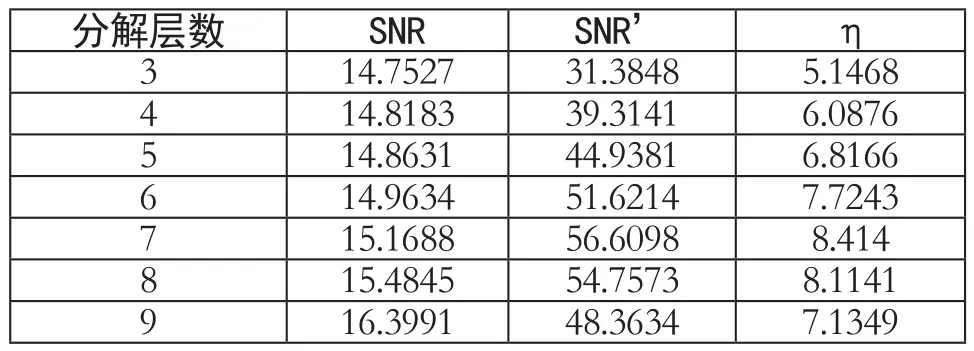
表1　分解层数不同条件下去噪效果系数

1.4小波母函数选择

在最优分解层数为7层的基础上，需要确定最优母小波，采用Symlets的sym1～sym15、Coifets的coif1～coif5和Daubechies的db1～db15等多种不同母小波，应用于仿真波形。经过对比分析，采用sym13作为小波母函数时，去噪的效果较好。获得的部分SNR和SNR*以及评估系数η如表2所示。

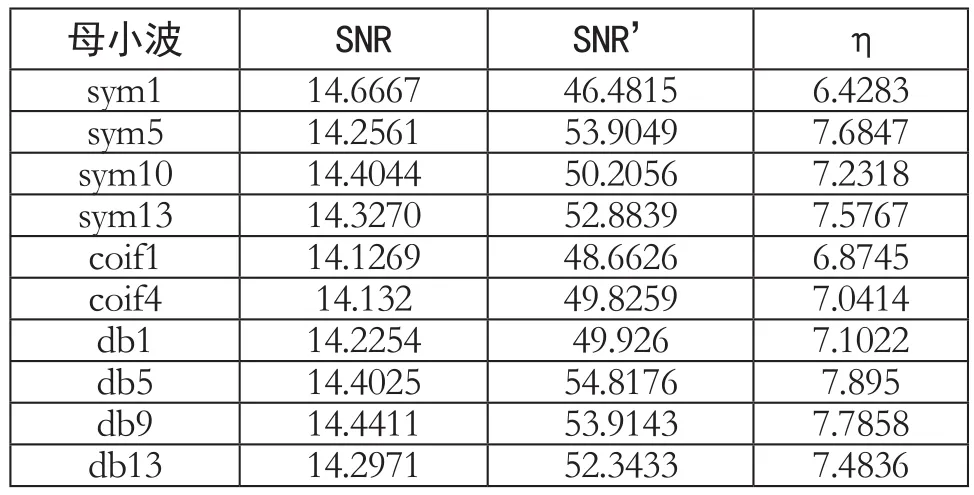
表2　母小波不同条件下过电压去噪效果系数

1.5阈值函数和阈值规则的选择

小波阈值去噪中阈值函数的选择和阈值的量化对去噪效果有很大影响［8-9］。传统小波阈值函数主要采用软、硬阈值函数。硬阈值法将其他小波系数置零并保留大于阈值的小波系数，硬阈值函数定义为

软阈值法置零小于阈值的各个小波系数，并将大于阈值的小波系数向零渐进，表达式为

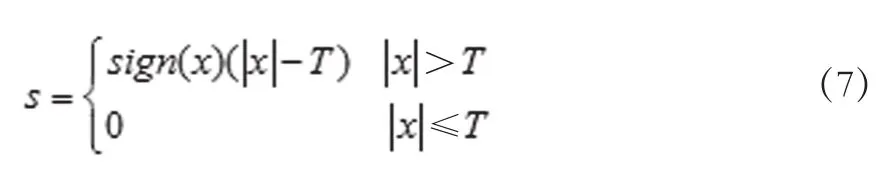
由上可知，硬阈值法能保留较多真实信号的高频特征，但由于不连续，在某些点上会产生间断，这会影响对真实过电压信号的处理。软阈值法虽然连续，但因为自身存在固定偏差，使得去噪效果也不尽人意。

针对软、硬阈值自身的缺陷，本文构造了一种新的阈值函数，该函数不但在小波域内是连续的，而且高阶可导，其函数表达式为

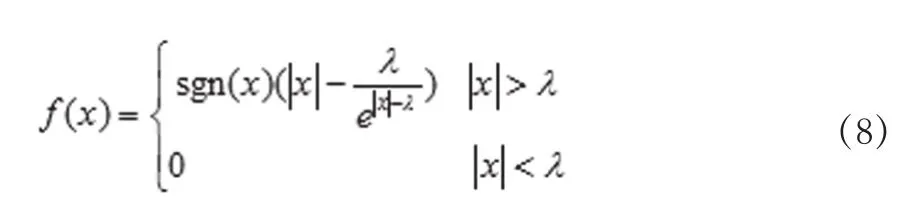
噪声作为方差未知的随机信号，在实际去噪前必须先对阈值的大小进行估计，通常有4种可供选择的阈值估计方法：固定阈值（sqtwolog）、基于Stein的无偏似然估计原理的自适应阈值选择（rigrsure）、启发式阈值（heursure）、极大极小阈值（minimaxi）［12］。

现场过电压信号中大量掺杂高斯白噪声，在去噪试验时，采用sqtwolog和heursure规则相较于采用比较完全，但部分高频信号会被错认为噪声而去除掉，minimaxi和SURE阈值规则去噪虽然只能将部分系数置零，但是去噪时显得更为有效。经综合分析考虑，采用sqtwolog规则，部分评估数据如表3所示。

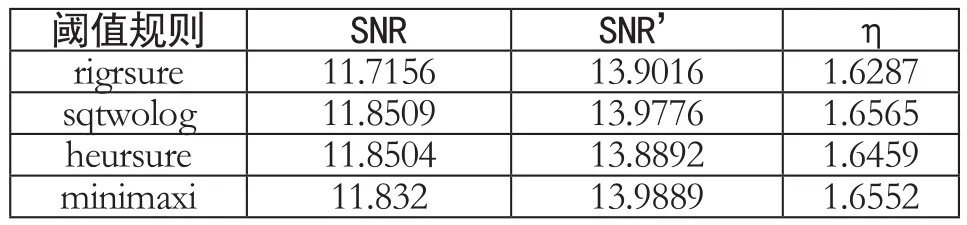
表3　不同阈值规则过电压模型评估系数

2　小波阈值去噪算例验证

2.1仿真波形去噪

采用本文提出的新阈值函数构造的算法，对仿真出的电压波形进行去噪处理，并同时与传统硬阈值和软阈值去噪对比分析。利用ATP-EMTP电磁暂态仿真软件建立110kV操作过电压模型，将所获得的无噪声波形导入MATLAB，并叠加噪声。仿真原始波形、叠加噪声后的波形、硬阈值去噪后的波形、软阈值去噪后波形和新阈值去噪后的波形图如图2所示。相关评估系数如表4所示。

表4　不同阈值函数条件下仿真模型评估系数

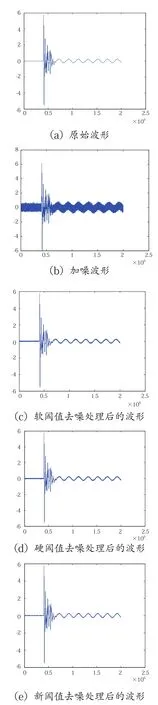
图2　不同阈值函数条件下仿真波形去噪

从仿真实例可以看出，新阈值函数去噪法的SNR和SNR*以及评估系数η均高于传统去噪法，相较于传统软阈值函数和硬阈值函数，新阈值函数的去噪效果明显较优，在该阈值函数下的小波阈值去噪算法可以获得更小的误差。

2.2实测波形去噪实例

为了说明本文中构造的阈值函数的实用性和有效性，采用传统软、硬阈值法以及本文中的新阈值方法对攀枝花某变电站实测过电压波形进行处理。从图3、图4中可以看出，新阈值函数处理后的波形毛刺较少，去噪较为彻底，还原效果系数也明显高于传统软、硬阈值去噪，并且也不存在硬阈值函数处理后出现的间断点。

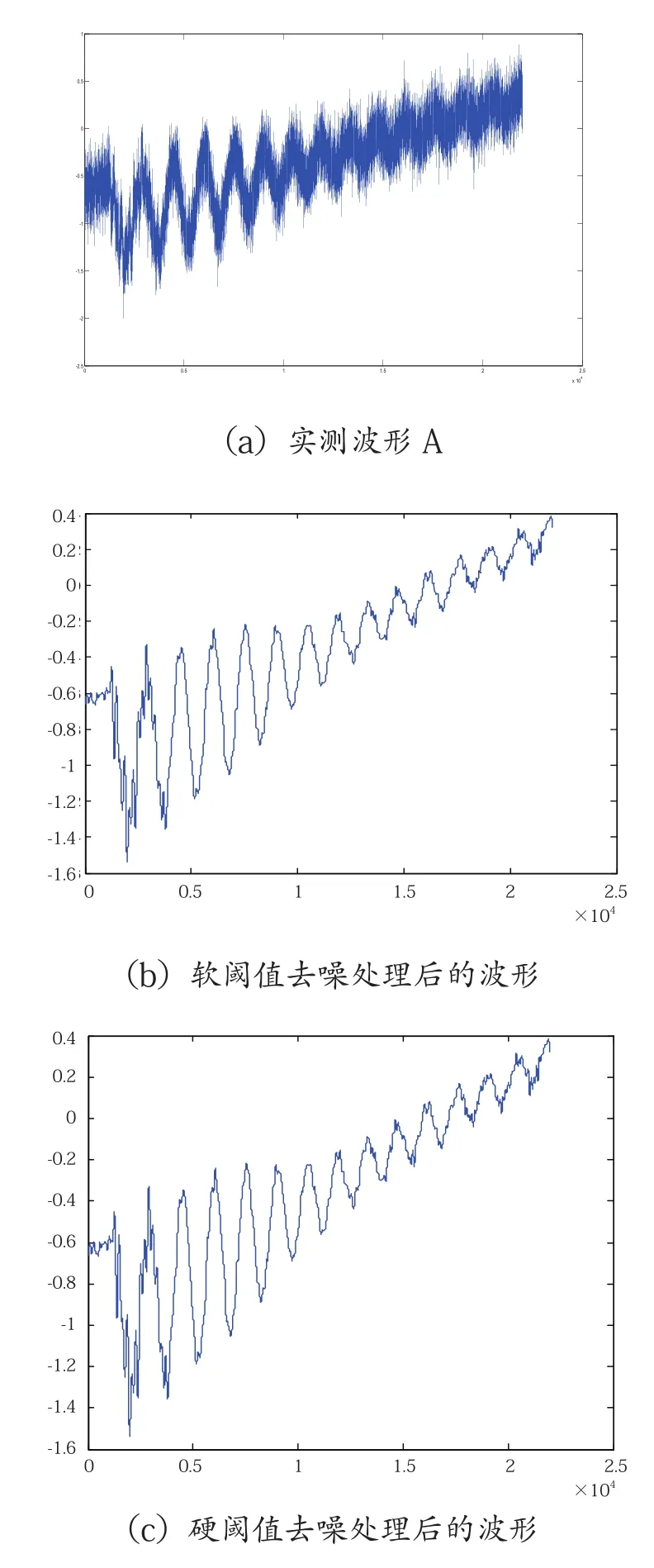
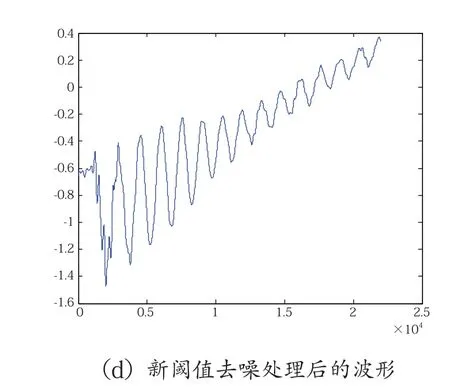
图3　不同阈值函数条件下实测波形A去噪

从表5、表6的相关评估系数可以看到，新阈值函数与传统软、硬阈值相比，信噪比明显增大，表明新阈值函数在最大化保留了信号特征量的同时又尽可能的去除了信号中的噪声。

表5　不同阈值函数条件下实测波形A去噪评估

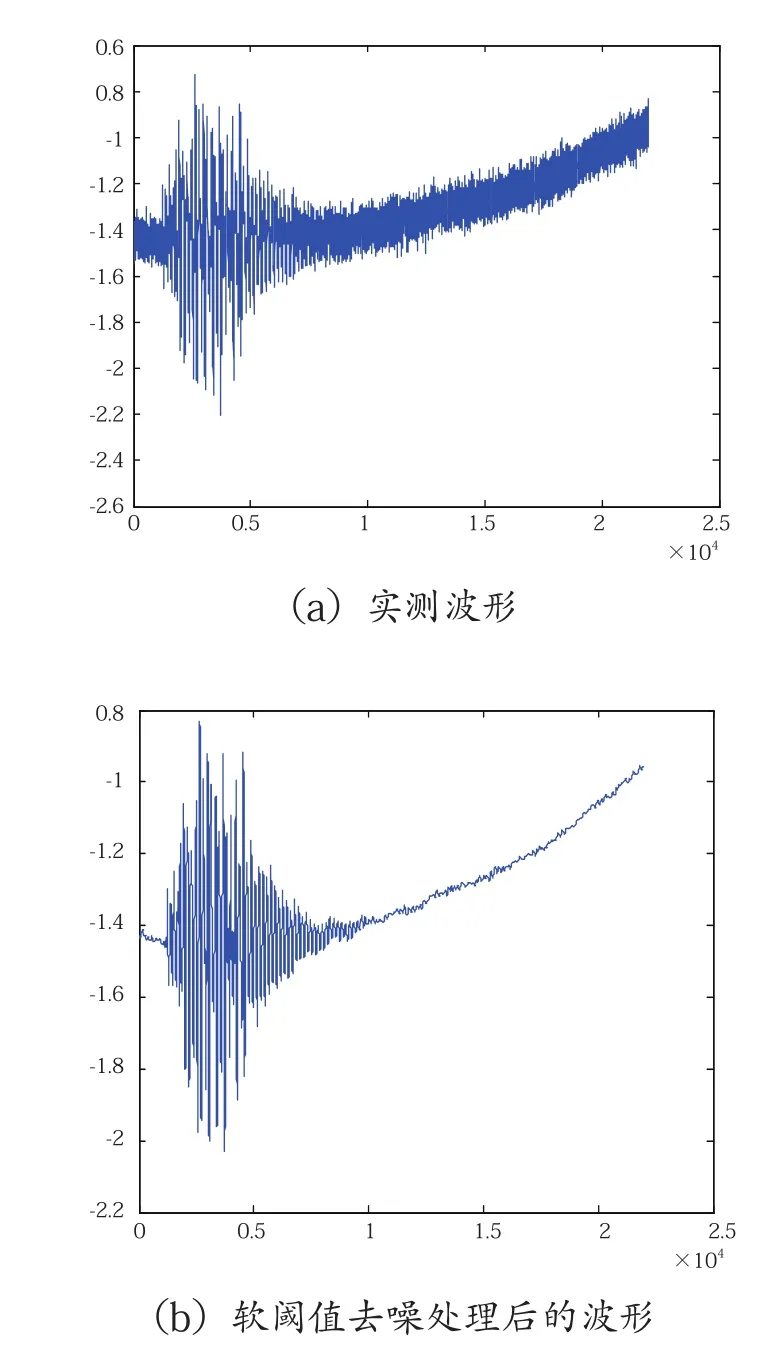
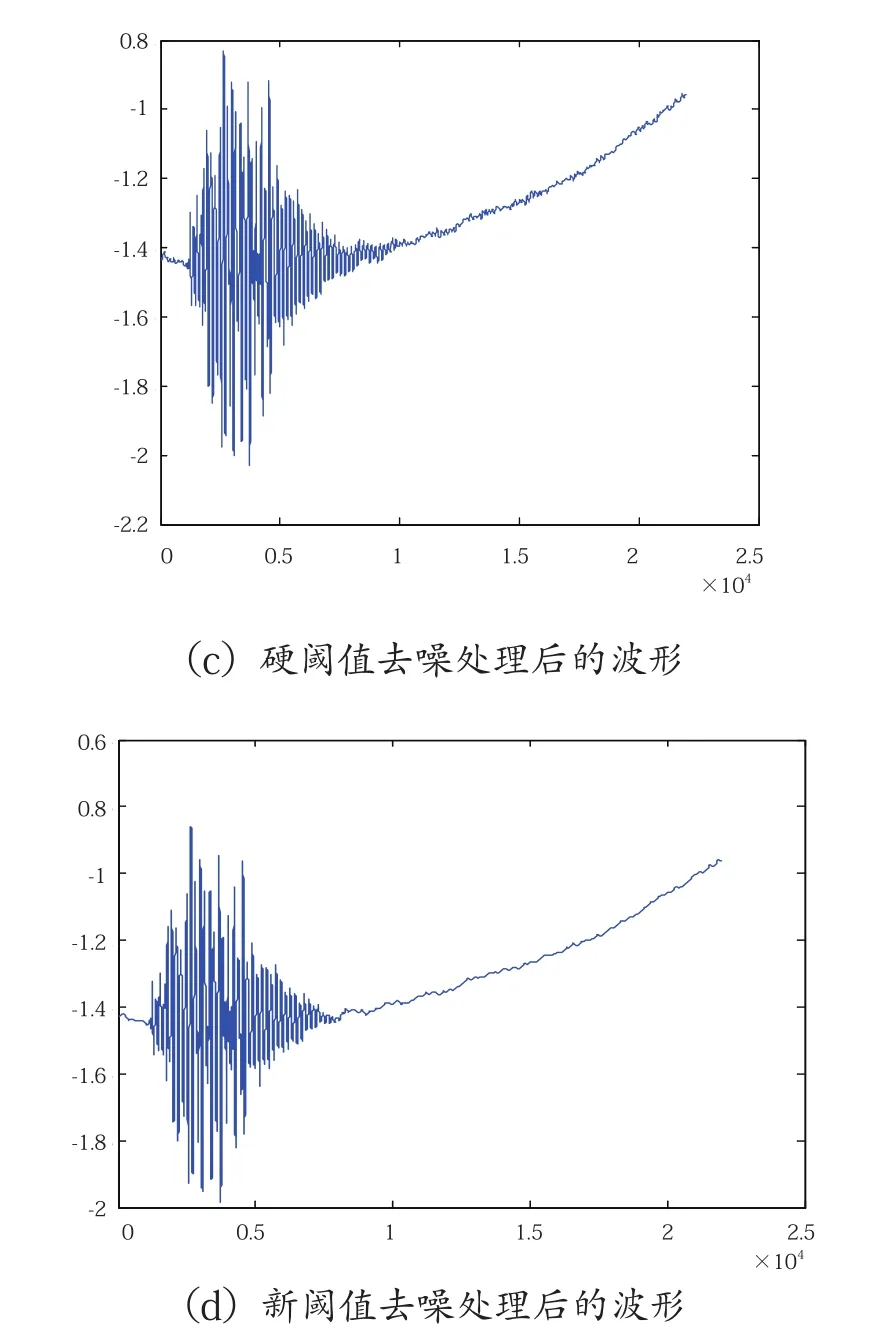
图4　不同阈值函数条件下实测波形B去噪

表6　不同阈值函数下实测波形B去噪评估

3　结束语

在对现场采集的过电压进行识别处理之前，需要对其进行去噪处理，本文在充分考虑传统阈值去噪缺陷的条件下构造了一种新的阈值函数，通过实例对比分析，新阈值函数克服了硬阈值函数不连续和软阈值函数固定偏差的缺点。通过仿真实验验证了该去噪方法对于高频过电压信号中的噪声有良好的去噪效果，在最大化保留了过电压信号的同时，又去除了信号中影响过电压信号后续处理的噪声，比传统软、硬阈值函数更好地提高了信号的信噪比。

［1］ 欧阳森，宋政湘，陈德桂，王建华.小波软阈值去噪技术在电能质量检测中的应用［J］.电力系统自动化2002（19）：56-60.

［2］ 李璟延，司马文霞，姚陈果，孙才新.染污绝缘子安全区泄漏电流检测中去除信号干扰方法［J］.电力系统自动化，2008（5）：85-89.

［3］ 钱勇，黄成军，陈陈，江秀臣.多小波消噪算法在局部放电检测中的应用［J］.中国电机工程学报，2007（6）：89-95.

［4］ DONOHO DL. De-noising by msoft-thresholding ［J］. IEEE Transactions on Information Theory，1995，41（3）：613-627.

［5］ 刘卫东，刘尚合，胡小锋，王雷.小波阈值去噪函数的改进方法分析［J］.高电压技术，2007（10）：59-63.

［6］ 崔华，宋国乡.基于小波阈值去噪方法的一种改进方案［J］.现代电子技术，2005（1）：8-10.

［7］ 吕瑞兰，吴铁军，于玲.采用不同小波母函数的阈值去噪方法性能分析［J］.光谱学与光谱分析，2004（7）：826-829.

［8］ 王蓓，张根耀，李智，王静.基于新阈值函数的小波阈值去噪算法［J］.计算机应用，2014（5）：1499-1502.

［9］ 赵瑞珍，宋国乡，王红.小波系数阈值估计的改进模型［J］.西北工业大学学报，2001（4）：625-628.

［10］ 李加升，黄文清，戴瑜兴.基于自定义阈值函数的小波去噪算法［J］.电力系统保护与控制，2008（19）：21-24.

［11］ 林京.基于最大似然估计的小波阈值消噪技术及信号特征提取［J］.仪器仪表学报，2005（9）：923-927.

（2016-1-20）