基于随机规划的并网风电穿透功率极限的计算

周晓玲　宁 哲　朱 博

（西安建筑科技大学华清学院 ）

基于随机规划的并网风电穿透功率极限的计算

周晓玲宁 哲朱 博

（西安建筑科技大学华清学院 ）

风电穿透功率极限的计算是含并网风电场的电力系统运行与规划的一个重要问题。文章采用数学优化算法来计算并网风电场穿透功率极限，基于随机规划建立风电穿透功率的求解模型，求取在一定的安全、稳定以及电能质量的约束条件下系统允许的风电场最大装机容量。另外，因为风速、负荷是动态变化的，所以文中以概率形式表示约束条件。并且针对问题的特点，求解模型时采用了遗传算法和Monte-Carlo仿真。最后以IEEE30节点系统为例进行算例分析，验证该算法的优越性。

风电穿透功率极限；随机规划；Monte-Carlo模拟；遗传算法

0　引言

随着人类对新能源的日益重视，风电技术得到飞速发展，风电的并网容量也越来越大，大规模的风电并网对系统电能质量以及系统运行的安全性稳定性等将产生一系列的重大影响［1-2］。因此，确定并网风电场的穿透功率极限是很有必要的。一般将风电穿透功率极限定义为风电场的最大装机容量占系统负荷的比值［2］。 目前主要用数字仿真法、基于频率静特性约束法、带约束的数学优化方法等来求解风电穿透功率极限。前两种方法都考虑不到负荷以及风速的动态变化［3-5］。

本文采用带约束的数学优化方法来计算并网风电场的穿透功率极限，在各种等式以及不等式约束下求解穿透功率极限。这样可以考虑所有可能的运行模型，假设风速的变化服从Weibull分布，节点负荷的变化服从正态分布。根据问题的特点应用基于Monte-Carlo模拟的改进遗传算法求解优化模型，最后在IEEE30节点系统上验该算法的有效性。

1　风电机组输出功率的计算模型

为了便于求解，本文用一台等效风电机来模拟风电场。风机输出功率与风速的关系可以近似用图1表示，公式表示如式（1）所示。

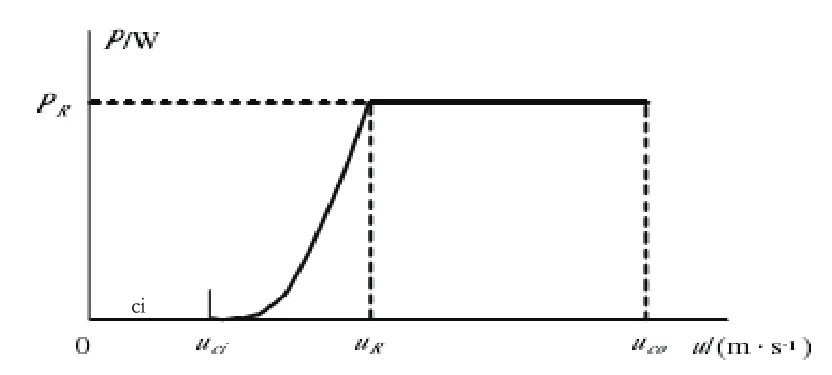
图1　风机输出功率/风速关系曲线

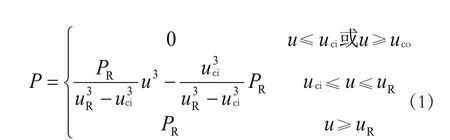
式中，u为风机轮毂高度处的风速；uR为额定风速；uci为切入风速；uco为切出风速；PR为额定输出功率。

概率密度方程为

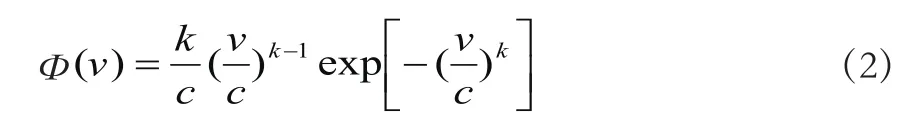
式中，k为形状系数，取值1.5～2.3之间；c反映了年平均风速大小。

2.基于随机规划的模型的建立

2.1.目标函数的确定

本文要求解并网风电场穿透功率极限，因此目标函数取为风电场的最大装机容量，即

2.2.约束条件

（1）等式约束

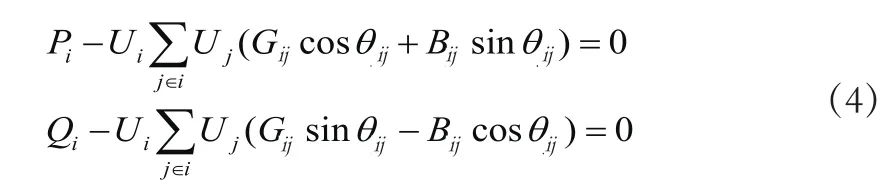
（2）不等式约束

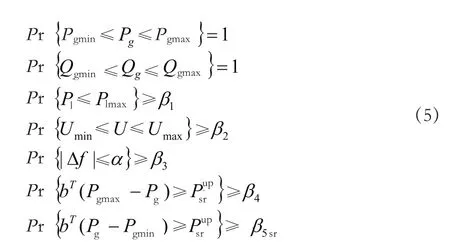
风电场最大装机容量即为在常规机组的出力、输电线路传输功率、电压偏差、系统的频率偏移、系统旋转备用容量等约束下，系统最多可接受的风电场容量，约束模型如下式中，Pg、Pgmin和Pgmax分别为常规机组的有功功率向量以及常规机组出力的上下限向量；Pl、Pgmax分别为传输线路的有功功率向量以及其传输容量极限；△为系统的频率偏移，为频率偏移极限；b为与Pg同维的列向量，对应于Pg中非零元素位置上的元素取1，其他元素为0；βl～β5为置信水平，代表着系统能够接受的风险的大小。

3　采用基于Monte-Carlo模拟的改进遗传算法求解模型

3.1Monte-Carlo模拟技术

Monte-Carlo模拟是一种实现随机系统抽样试验的技术，其操作原理是根据给定的概率分布来抽取一定样本的随机变量［10］。文中的Monte-Carlo仿真模拟主要用于检验约束条件是否成立，下面介绍应用Monte-Carlo模拟检验线路的传输功率约束

风速服从Weibull分布，负荷服从正态分布，样本规模为n，则Monte-Carlo模拟算法如下：

1）设jsq=0；

2）应用随机模拟技术生成风速样本［v1，v2……vn］、负荷样本［P1D，P2D……PnD］,利用式（1）计算风电场的输出功率；

3）应用节点功率对线路的灵敏度函数计算P1，如果P1≤Plmax，jsq=jsq+1；

4）重复步骤（2）～（4）一次；

5）如果pr｛P1≤Plmax｝=jsq/n≥β1，则计算结束。

3.2基于Monte-Carlo模拟的改进遗传算法

对于求最优化问题，求解方法主要有传统算法和智能算法，本文以改进遗传算法为例详细说明求解风电穿透功率极限的过程。利用遗传算法求解机会约束规划有以下关键问题。

（1）解的编码

（2）种群初始化

风电场的装机容量不会很大，超不过系统的负荷水平，这样就限定了解的搜索空间［12］。随机产生一个染色体，应用Monte-carlo模拟检验是否满足各约束条件；若满足，则作为一个个体进入种群。重复popsize（群体规模）次，完成种群初始化。

（3）带有惩罚项的适应度函数

适应度是根据目标函数确定的用于区分群体中个体好坏的标准［13］。对上面所建立的目标函数采用惩罚策略，采用加法形式构造带有惩罚项的适应值函数，变量仍为风电机装机容量，设为P,但是建立的目标函数为

式中，w为等式约束的惩罚算子；r为不等式约束的惩罚算子；g（x）为功率平衡方程；h（x）为不等式约束。

（4）改进的选择、交叉、变异操作

在选择方法上，采用了基于最优保存策略的最佳保留选择，按轮盘赌选择方法［14］执行遗传操作可以保证遗传算法的优化的最终结果是种群中出现的最高适应度的个体。在交叉操作上采用单点交叉操作，增加种间竞争以避免陷入局部最优。在变异操作上将进化的过程分为渐进、突变两个不同的阶段，突变阶段的变异概率高；渐进阶段变异概率低。这样采用动态变异算子使得突变阶段提高了群体多样性，渐进阶段则加快了全局收敛速度。

3.3算法流程

遗传算法基本流程如图2所示。

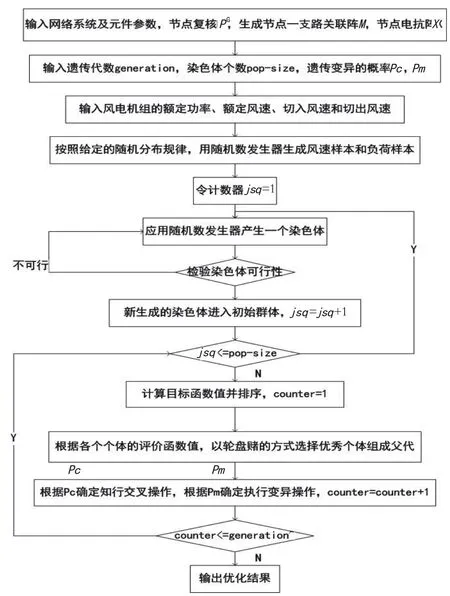
图2　基于Monte-carlo模拟的遗传算法流程图

4　算例验证

系统参数：以IEEE30节点系统［9］为例对文中所建模型和算法进行验证。IEEE30节点系统的网络拓扑图如图3所示。机组参数取自Matpower，系统的总负荷为2.862,共有6个常规机组1，2，5，8，11，13。假设5、8号机组出力分别为0.45、0.35；1号作为调频机组；2、11、13号机组参与优化，表1为常规机组有功出力上下限值。在计算中考虑了各节点负荷服从正态分布，均值和方差可以参考文献［5］。风速参数k=2.0，c=7.5，风速以及负荷的样本规模取为n=1000。

算法参数设置：遗传算法的群体规模取popsize=30，遗传代数generation=200，交叉概率Pc=0.7，变异概率1～50代Pm=0.1，50～100代Pm=0.05，150～200代Pm=0.01。

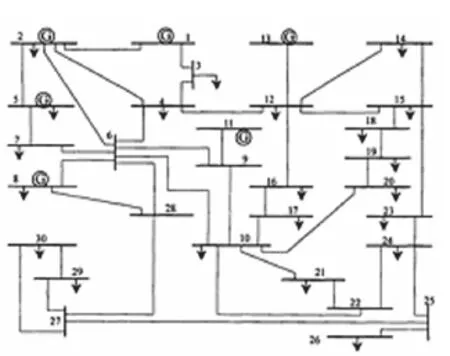
图3　IEEE30节点网络拓扑图

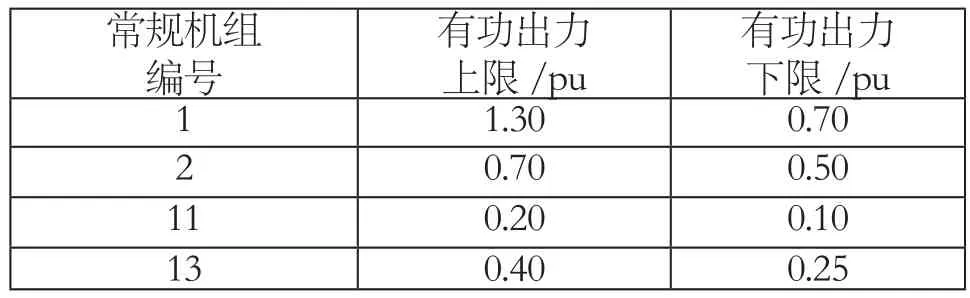
表1　常规机组参数

为了对影响并网风电场穿透功率极限的因素进行分析，设计了以下几个方案：

方案一：只在一个节点并入风电场，随机选取节点16、22、28、30，βl～β5分别取0.92、0.96、1.00，vci=5m/ s，vco=20m/s。进化的最优结果如表2所示，此外表3还给出了βl～β5=0.96时，风电场从不同节点接入时2、11、13号机组的最优出力。

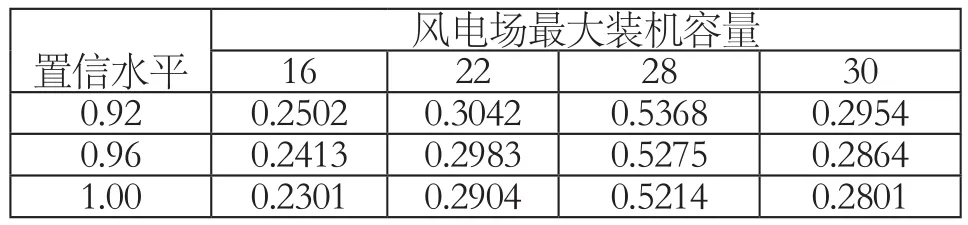
表2　进化最优结果

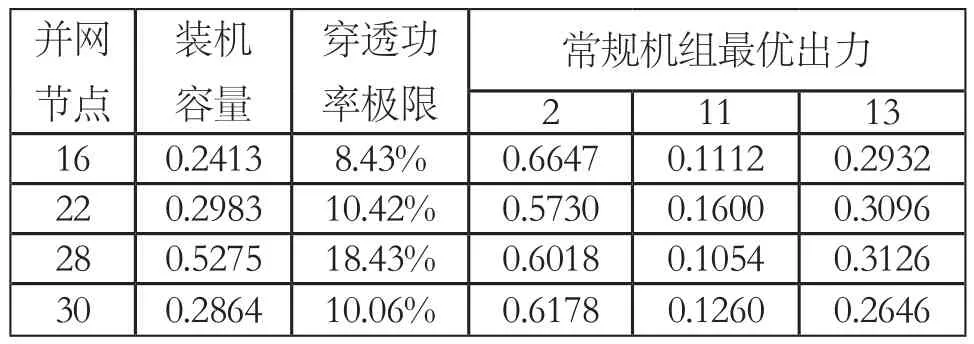
表3　常规机组出力的优化结果

方案二：方案一中的条件不变，分别将常规机组的出力上限提高10%，下限减小10%，其进化的优化结果见表4。

表4　

方案三：方案一中的条件不变，改变Weibull分布参数，若取c=7.5,其进化的优化结果见表5。若改变k，其进化的最优结果见表6。

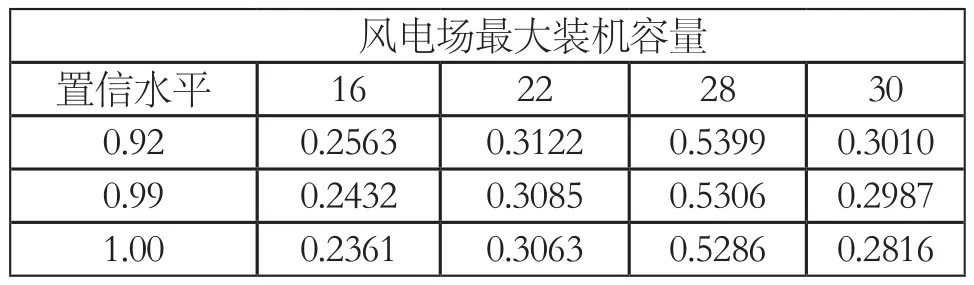
表5　

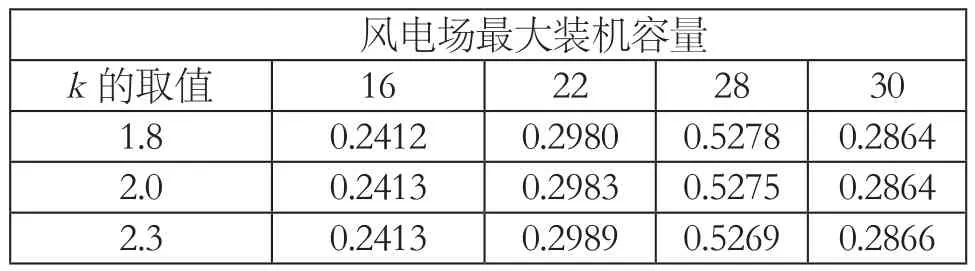
表6　

比较分析上面的表2～6中的计算结果，不难得到以下几点结论：

1）由表2的计算结果可知：风电场从不同节点并入系统，风电场的最大装机容量明显不同；表3给出了置信水平为0.96时，风电场从不同节点接入时，常规机组的最优出力，这对含风电的电网运行与规划具有重要意义。

2）从表2、表4中可看出：放宽对常规机组的出力上下限的约束后，各节点的风电场的最大装机容量有较大提高。且各节点的提高水平不同，这说明风电穿透功率水平受到常规机组出力限制的同时也受到网络结构的约束。

3）对比表2与表5的计算结果表明：c的取值较小，则当地的风场平均风速也较小，但系统可接受的风场最大装机容量有一定程度的提高，这是因为：假设风场装机容量相同，如果风速的变化范围越广，对系统的扰动也会越大，这样将会限制风电场的装机容量。且由表6知风速的Weibull形状系数k取不同的数值对系统可以接受的最大风电装机容量影响不明显。

5　结束语

1）利用本文所建模型、优化算法可以直接求解出在负荷、风速动态变化的情况下风电穿透功率的极限值。

2）文中定量分析了风电场并网节点的选择、风电场的风速分布规律、常规机组的出力限制等因素对风电穿透功率水平的影响。另外，本文方法的另一个优点是在计算风电场最大装机容量的同时给出了其他常规机组的最优出力，这对含风电场的电网的运行规划具有重要意义。

［1］ 彭莎. Cvar理论在风电场穿透功率极限中的应用研究［D］. 长沙：长沙理工大学，2012.

［2］ 李文娟.风电并网及其穿透功率极限的研究［D］.武汉：华中科技大学，2009.

［3］ 吴俊玲，周双喜，孙建锋，等. 并网风力发电场的最大注入功率分析［J］. 电网技术.2005， 28（20）：28-32.

［4］ 吴俊，李国杰，孙元章. 基于随机规划的并网风电场最大注入功率计算［J］.电网技术，2007，31（14）：15-19.

［5］ 雷亚洲，王伟胜，印永华，等. 基于机会约束规划的风电场穿透功率极限的计算［J］.电网技术，2003，22（5）：32-35.

［6］ Chen Z.Issues of Connection Wind Farms into Power System［C］.IEEE/PES Transmission and Distribution Conference and Exhibition-Asia and Pacific，China ，2006.

［7］ 刘德坤，于磊，周鑫. 风电场接入容量分析与计算［J］.华北电力技术， 2010.

［8］ 黄红选. 数学规划［M］.北京：清华大学出版社， 2005.

［9］ 张伯明，陈寿孙. 高等电力网络分析［M］.北京：清华大学出版社， 1996.

［10］ Charne A.Chance-constrained programming［J］. Management Science， 1959，6（1）：73-79.

［11］ Ha Thu Te， Thang Quang Nguyen. Augmenting Wind Power Penetration and Grid Voltage Stability Limits Using ESS： Application Design， Sizing， and a Case Study［J］. IEEE Transactions Power Systems ， Feb，2012：27（1）：161-171.

［12］ 雷英杰，张善文，李续武，等.MATLAB遗传算法工具箱及应用［M］.西安：西安电子科技大学出版社，2005.

［13］ 朱雪玲，张洋，李强，等. 基于遗传算法的风电场最优接入容量问题的研究［J］. 电力系统保护与控制，2011，38（9）：55-60.

［14］ Ala A Tamimi，Anil Pahwa，Shelli Stawett，et al.Maximizing Wind Penetration Using Voltage Stability Based Methods for Sizing and Locating New Wind Farms in Power System［J］，Power System Protection and Control，2010.

［15］刘鑫，栗文义，许立杰，等. 并网风电最大注入功率影响因素研究［J］. 华东电力，2012，40（3）：398-400.

（2016-01-28）