偏最小二乘建模及其多重共线抑制能力分析

杨春华，杨玲（保山学院数学学院，云南保山678000）

偏最小二乘建模及其多重共线抑制能力分析

杨春华，杨玲
（保山学院数学学院，云南保山678000）

首先，分析偏最小二乘法解决问题的思路，进而从数学角度刻画偏最小二乘法的四步建模过程.然后，利用数学归纳法证实偏最小二乘法对多重共线的抑制能力.最后，以某地区的供水能力评价为研究实例，证实偏最小二乘法的有效性.结果表明：偏最小二乘法完全适用于多变量复杂关系的求解.

偏最小二乘；数学归纳法；多重共线；回归分析

在参数估计和回归分析领域，多个自变量和多个因变量间的关系是一个非常复杂的问题［1－3］.采用最小二乘法等常规分析方法，难以达到预期的效果.这是因为多个自变量之间，多个因变量之间往往存在多重相关性，即多重共线性［4－10］.偏最小二乘回归分析利用信息综合筛选技术进行回归模型的构建，有效规避了原有变量的多重相关问题［11－15］.本文对偏最小二乘回归分析方法及其建模过程进行研究.

1 偏最小二乘法

假设分析的问题中，存在m个自变量，其集合可表述为｛p1，p2，…，pm｝；存在n个因变量，其集合可表述为｛q1，q2，…，qn｝.根据统计方法获取m个自变量和n个因变量的原始数据后，用P，Q对这些数据进行描述.其后，偏最小二乘法的执行，就是在数据对象P和Q上进行.

首先，在数据对象P，Q上各自提取1个主成分，分别用α1，β1表示.实际上，α1是集合｛p1，p2，…，pm｝中各个元素的1个线性组合，而β1则是集合｛q1，q2，…，qn｝中各个元素的1个线性组合.在提取α1，β1时，需满足2个条件：第一，α1，β1要尽可能多地表征数据对象P，Q的变异特征；第二，α1，β1的关联水平可以达到最高.然后，在提取α1，β1后，偏最小二乘法进一步对数据对象P，Q执行有关α1，β1的回归检验.如果回归检验满足既定的精度要求，偏最小二乘法执行完毕；如果回归检验没有满足既定的精度要求，则需要根据P，Q被α1，β1描述后的剩余信息，再次执行成分提取，直至满足检验精度.最后，偏最小二乘法会为数据对象P提取出i个成分，即α1，α2，…，αi；偏最小二乘法为数据对象Q提取出j个成分，即β1，β2，…，βj.多因变量集合｛q1，q2，…，qn｝中任一因变量，可描述为α1，α2，…，αi的回归关系.

2 多变量问题的偏最小二乘建模

应用偏最小二乘法，对多变量问题进行建模求解时，有如下4个步骤.

步骤1 对数据对象P，Q执行标准化处理，进一步得到自变量和因变量矩阵P0，Q0，其过程为

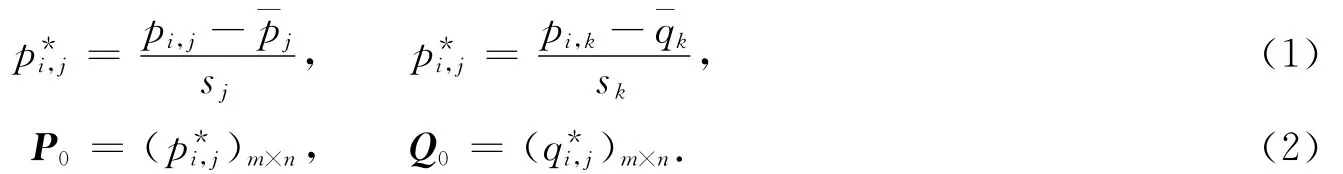
式（1），（2）中：珚pj，珔qk为均值；sj，sk为标准差.

步骤2 从自变量矩阵P0和因变量矩阵Q0中提取第1个主成分，即

式（3）中：a1为P′0Q0Q′0P0的特征向量；b1为Q′0P0P′0Q0的特征向量.

数据对象P，Q和第1个主成分的回归关系，可以描述为

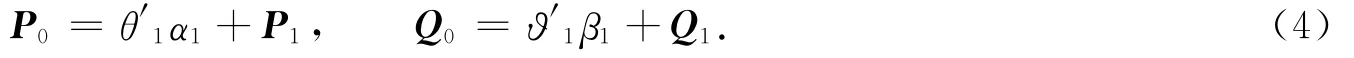
式（4）中：θ1，1为回归方程中的回归系数.

步骤3 根据第1个主成分的回归方程，可以递推第2个主成分的回归方程，即

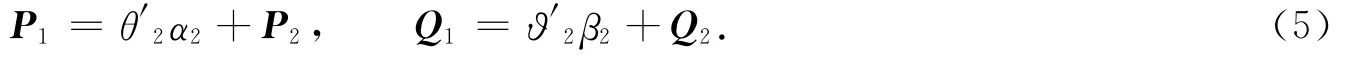
以此类推，可以获得第λ个主成分的回归方程，即

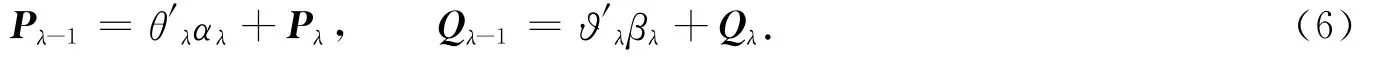
步骤4 假设最终数据对象P的秩是λ，则有

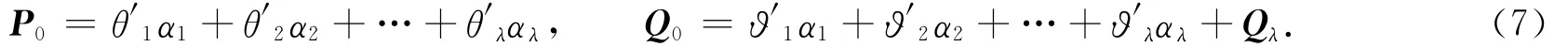
最终，因变量q＊的有关自变量的偏最小二乘形式为

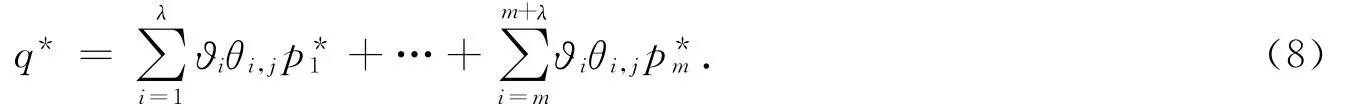
3 偏最小二乘的多重共线抑制能力分析

对多重共线的抑制能力，是偏最小二乘法的重要特征.为了证实偏最小二乘法在此方面的性能，只要证明偏最小二乘法提取的多个成分之间相互直交.据此，考察如下命题是否成立.

命题1 当h≠l时，偏最小二乘法获得的多个成分α1，α2，…，αλ相互直交，即存在α′lαh＝0.

证明 采用数学归纳法证明此命题.

首先，证明α1，α2之间是否是直交的，即是否存在α′1α2＝0.

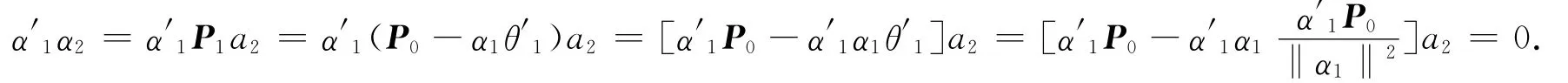
至此，α1，α2之间的直交关系得到证实.根据数学归纳法，只要假设在α1，α2，…，αh直交的前提下，证实α1，α2，…，αh＋1也是直交的，命题中的结论就可以得到证实.

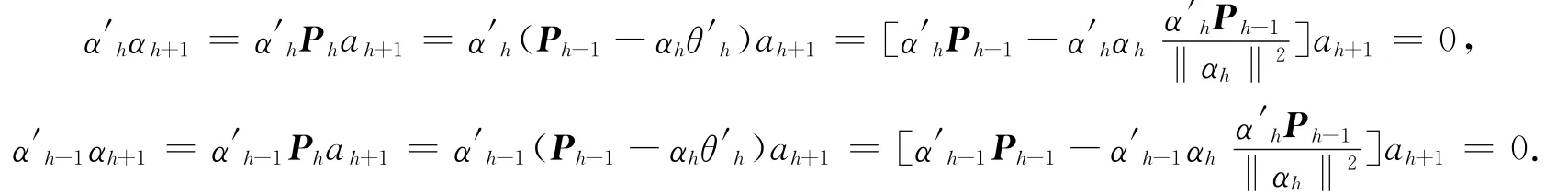
因α′h－1αh＝0，有

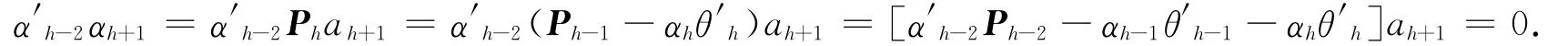
至此，α1，α2，…，αλ之间的直交关系得到证实.在原始问题的回归分析中，那些变量都可以表征为α1，α2，…，αλ之间的回归组合，而这些成分又是相互直交的，这就不会存在多重共线问题.

4 偏最小二乘建模在实际问题中的应用

假设某地区供水能力的影响因素分别用p1，p2，…，pn表示，从而构建1个多影响因素集合P＝｛p1，p2，…，pn｝.假设某地区供水能力，可以有多个指标表征，如q1，q2，…，qm，从而构建一个多指标评价集合Q＝｛q1，q2，…，qm｝.供水能力影响因素和供水能力评价指标，可以分别得到2个观测矩阵，即

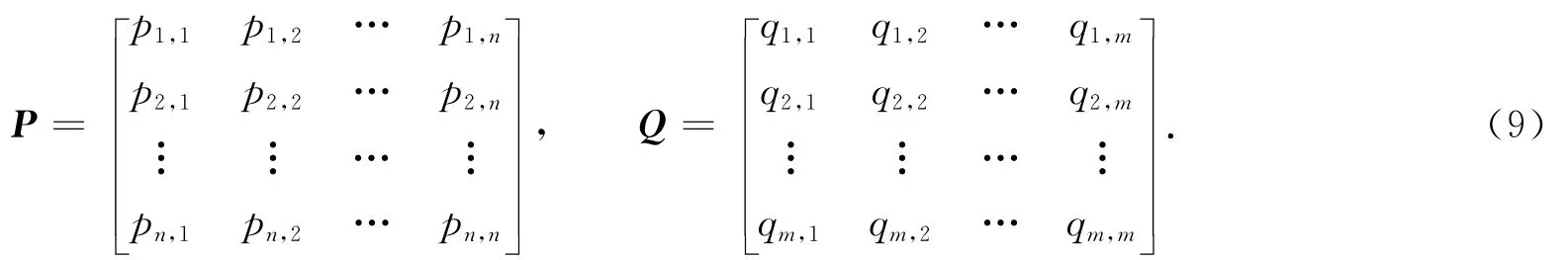
因此，某地区供水能力的分析、评价与预测，就演变为P，Q的偏最小二乘模型求解.

某地区主要依靠3个水库进行供水，按照地理位置，分为东区水库、西区水库和南大坝水库.为此，设计如下指标：q1～q3分别为该地区东部、西部、南部用水量需求；p1为该地区东部水库供水量；p2为该地区东部水库泄洪量；p3为该地区西部水库供水量；p4为该地区西部水库泄洪量；p5为该地区南部水库供水量；p6为该地区南部水库泄洪量.上述参数主要来源于2000－2015年度统计数据，如表1所示.

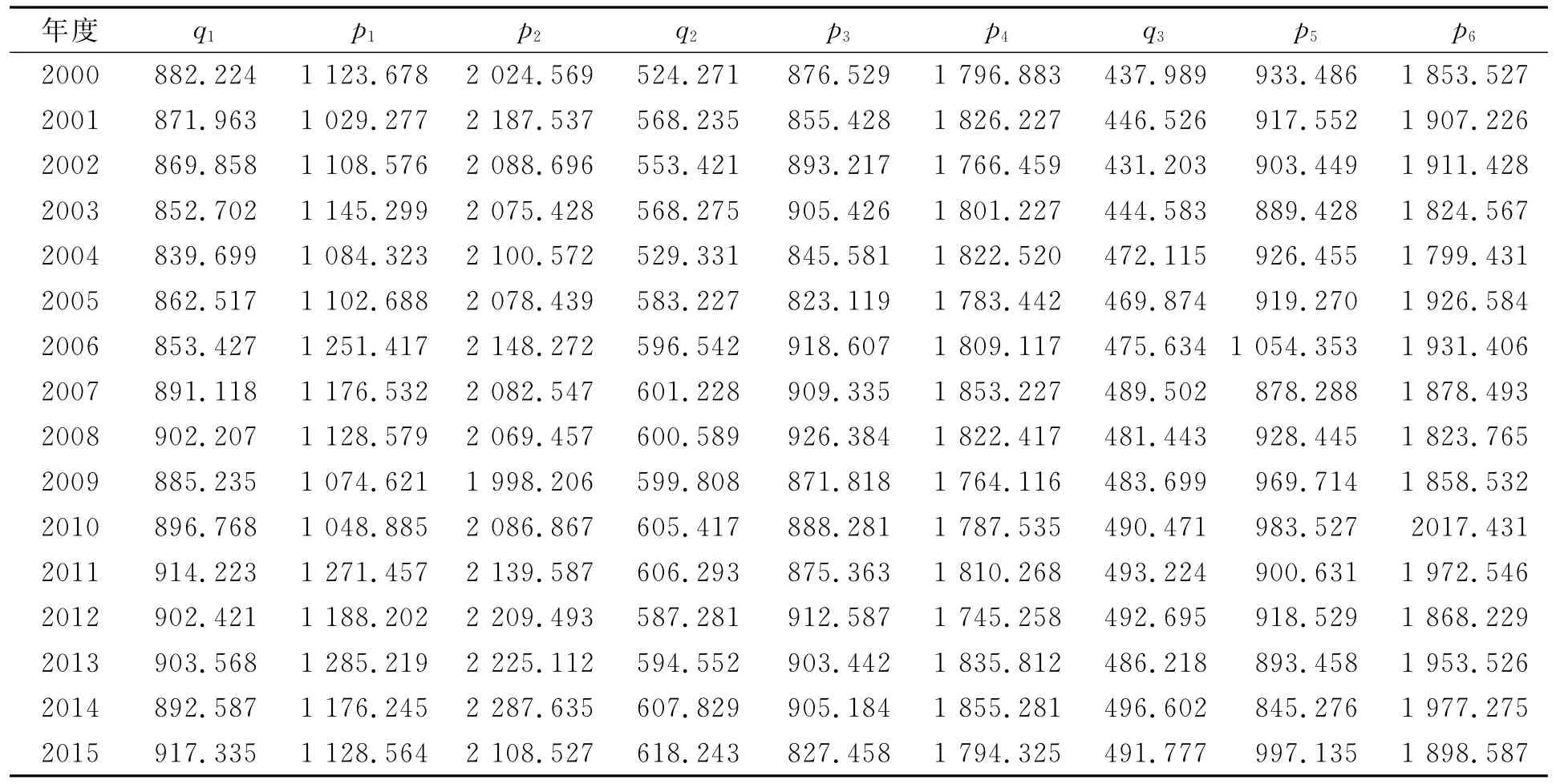
表1 主要参数的年度数据Tab.1 Main parameters of the annual data 万m3

将表1的数据，代入供水能力偏最小二乘模型，进而执行偏最小二乘分析，回归系数如表2所示.由表2可知：p1，p2和p1的关联程度最高；p3，p4和q2的关联程度最高；p5，p6和q3的关联程度最高.该地区供水能力影响因素P和供水能力Q的复相关系数为0.762 2，这表明P，Q之间密切相关.

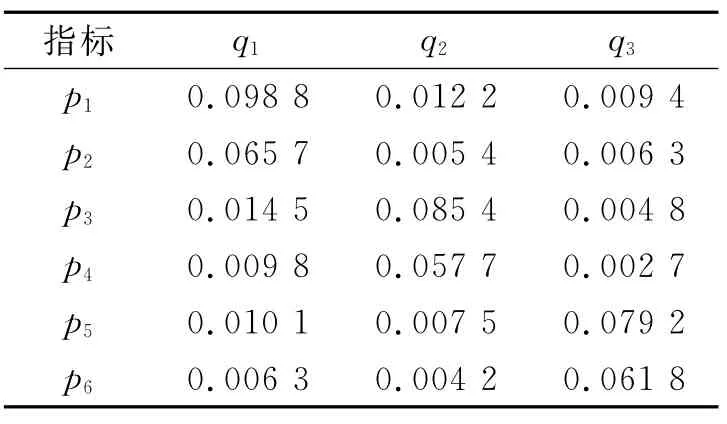
表2 偏最小二乘得出的回归系数Tab.2 Regression coefficient obtained by using partial least squares

在上述模型下，进一步以供水能力影响因素（p1，p2，p3，p4，p5，p6）年度环比值预测其在2016－2018年度的变化，根据关联系数及偏最小二乘模型预测该地区供水能力（，）在2016－2018年度的变化；进而根据供水能力（q1，q2，q3）年度环比预测其在在2016－2018年度的变化，算出该地区未来3年富余水量的情况（Δq1，Δq2，Δq3），结果如表3所示.由表3可知：未来3年中，该地区的东部、西部、南部供水量都有盈余，能够满足当地供水的需求.

表3 2016－2018年度的预测结果Tab.3 Forecast results for 2016－2018 万m3

5 结束语

梳理了偏最小二乘法的建模过程及其解决实际问题的思路，重点分析了其对多重共线的抑制.以某地区的供水能力评价为研究实例，其结果充分证明偏最小二乘分析具有多重共线抑制能力，对于多个变量的复杂关系求解具有较强的适用性.

［1］ ADRIANO D A G，SCHENONE A V.Unfolded partial least squares／residual bilinearization combined with the successive projections algorithm for interval selection：Enhanced excitation－emission fluorescence data modeling in the presence of the inner filter effect［J］.Analytical and Bioanalytical Chemistry，2015，22（5）：30－37.

［2］ MOKHTARI A，KEYVANFARD M，EMAMI I.Simultaneous chemiluminescence determination of citric acid and oxalic acid using multi－way partial least squares regression［J］.RSC Advances，2015，37（5）：29214－29221.

［3］ ELDEN L.Computing frechet derivatives in partial least squares regression［J］.Linear Algebra and Its Applications，2015，473（11）：316－338.

［4］ ADJORLOLO C，MUTANGA O，CHO M A.Predicting C3and C4grass nutrient variability using in situ canopy reflectance and partial least squares regression［J］.International Journal of Remote Sensing，2015，36（6）：1743－1761.

［5］ TZANAKAKIS V A，MAUROMOUSTAKOS A，ANGELAKIS A N.Prediction of biomass production and nutrient uptake in land application using partial least squares regression analysis［J］.Water，2015，7（1）：1－11.

［7］ KUANG Boyan，TEKIN Y，MOUAZEN A M.Comparison between artifical neural network and partial least squares for on－line visible and near infrared spectroscopy measurement of soil organic carbon pH and clay content［J］.Soil and Tillage Research，2015，146（8）：243－252.

［8］ 吴瑞红，王亚丽，张环冲，等.一种基于最小二乘支持向量机的葡萄酒品质评判模型［J］.华侨大学学报（自然科学版），2013，34（1）：30－35.

［9］ 魏引尚，郑活勃，王宁.采空区自燃“三带”特征的最小二乘法分析［J］.西安科技大学学报，2015，35（2）：159－164.

［10］ 胡德，郭刚正.最小二乘法、矩法和最大似然法的应用比较［J］.统计与决策，2015，33（9）：20－24.

［11］ 宋媛媛，王萍，张庆芳，等.基于最小二乘法的TD－LTE传播模型校正研究［J］.电子测量技术，2015，38（1）：123－125.

［12］ 李鑫，张跃强，刘进博，等.基于直线段对应的相机位姿估计直接最小二乘法［J］.光学学报，2015，44（6）：203－213.

［13］ 陈明晶，方源敏，陈杰.最小二乘法和迭代法圆曲线拟合［J］.测绘科学，2016，41（1）：194－197.

［14］ 王鹏，刁山菊，张季谦.基于最小二乘法的单摆实验数据处理［J］.安庆师范学院学报（自然科学版），2015，36（1）：136－139.

［15］ 张开远，周孟然，闫鹏程，等.基于最小二乘法的pH值温度补偿系统设计［J］.传感器与微系统，2015，34（5）：109－111.

（责任编辑：钱筠 英文审校：黄心中）

Partial Least Squares Modeling and
Its Multiple Collinear Inhibition Capability Analysis

YANG Chunhua，YANG Ling
（School of Mathematics，Baoshan University，Baoshan 678000，China）

Firstly，by analyzing the thinking route to solve the problem of the partial least square method，the authors describe four modeling steps to the partial least square method.Finally，we confirmed the inhibition ability of partial least squares method for multiple collinear by using the mathematical induction method.By evaluating the water supply capacity of an area as a case study，it really shows the validity of the partial least squares method.Results in this paper shows that partial least squares method is completely applicable to the solution of multi variable complex relationships.

partial least squares；mathematical induction；multiple collinear；regression analysis

O 625.63

A

1000－5013（2016）04－0523－04

10.11830／ISSN.1000－5013.201604027

2016－05－05

杨春华（1973－），男，副教授，主要从事最优化理论及其应用的研究.E－mail：378667756＠qq.com.

云南省教育厅科学研究基金资助项目（2012Y258）