《数据的波动程度》测试题
2016-08-23沈红菊
沈红菊
A.① B.② C.③ D.②③
*7.某同学5次上学途中所花的时间(单位:min)分别为x,y,10,11,9。已知这组数据的平均数为10,方差为2,则|x-y|的值为( )。
A.1 B.2 C.3 D.4
二、填空题(每小题4分,共28分)
8.一组数据-1,0,1,2,3的方差是____。
9.已知一个样本1,3,5,x,2。若它的平均数为3,则这个样本的方差是____。
10.某超市出售三种品牌的面粉。在它们的包装袋上,质量分别标有(25±0.1)kg,(25±0.2)kg,(25±0.3)kg的字样。从中随意抽取两袋,它们的质量最多相差____kg。
11.若一组数据-2,0,2,5,a的最大值与最小值的差是8,那么a的值是____。
12.现有A,B两个班级,每个班级各有45名学生参加一次测试。每名参加者可获得0,1,2,3,4,5,6,7,8,9这几种不同的分值中的一种。A班的成绩如表3所示。B班的成绩如图1所示。
(1)观察可知,____班成绩的方差较大。
(2)若两班合计共有60人及格。则参加者最少获____分才可以及格。
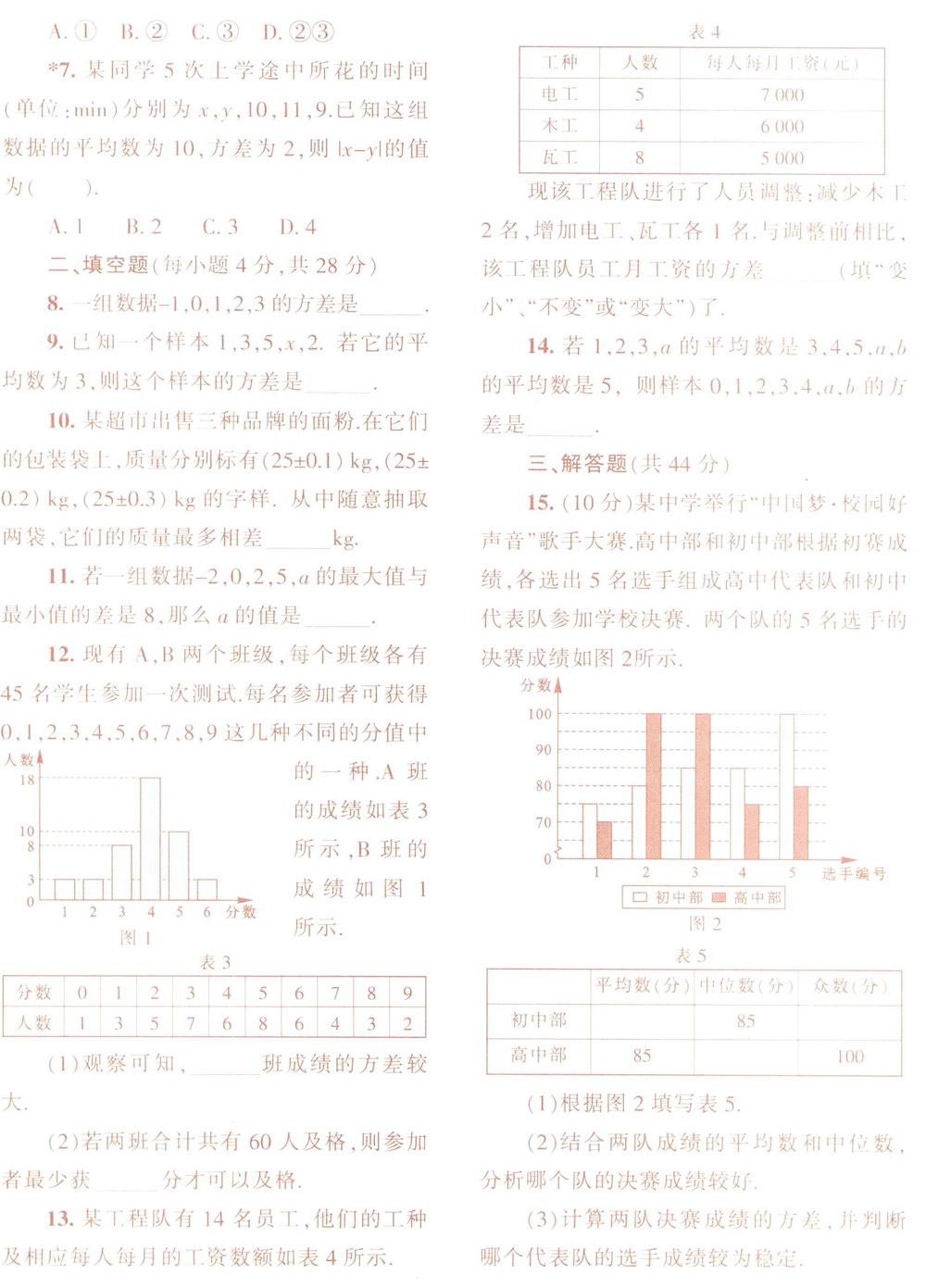
13.某工程队有14名员工,他们的工种及相应每人每月的工资数额如表4所示。
现该工程队进行了人员调整:减少木工2名,增加电工、瓦工各1名,与调整前相比。该工程队员工月工资的方差____(填“变小”、“不变”或“变大”)了。
14.若1,2,3,a的平均数是3,4,5,a,b的平均数是5,则样本0,1,2,3,4,a,b的万差是____。
三、解答题(共44分)
15。(10分)某中学举行“中国梦·校园好声音”歌手大赛。高中部和初中部根据初赛成绩,各选出5名选手组成高中代表队和初中代表队参加学校决赛。两个队的5名选手的决赛成绩如图2所示。
(1)根据图2填写表5。
(2)结合两队成绩的平均数中位数。分析哪个队的决赛成绩较好。
(3)计算两队决赛成绩的方差,并判断哪个代表队的选手成绩较为稳定。