数据的集中与离散

田载今

从计算结果可知，甲、乙的平均训练成绩差距不大，甲比乙略高。

（2）将甲的全部训练成绩（共100个）按环数从小到大依次排列，这100个数据中处于正中间位置的是第50个数据7和第51个数据8。这两数的平均数为7.5，即为甲训练成绩的中位数。

将乙的全部训练成绩（共99个）按环数从小到大依次排列，这99个数据中处于正中间位置的是第50个数据8，即为乙训练成绩的中位数。

从计算结果可知，一般情形下，甲发挥中等水平时成绩介于7环和8环之间的可能性较大，乙发挥中等水平时成绩是8环的可能性较大。

（3）在甲的全部训练成绩（共100个）中，出现次数最多的是7环（26次），7即这组数据的众数。

在乙的全部训练成绩（共99个）中，出现次数最多的是7环（25次）和8环（25次），7和8即这组数据的众数。

从计算结果可知，虽然每次射箭成绩可能会有变化，但在一般情形下，甲射中7环比射中其他环数的可能性要大，乙射中7环或8环比射中其他环数的可能性要大。

（4）由前面的平均数及方差公式，可得s²_甲≈1.95，s²_乙≈1.84。

从训练成绩的方差看，甲略大于乙，这说明甲的数据比乙的数据的离散程度略高，也即成绩的起伏略大。乙的成绩相对来说稳定些。

从上面这个例子可以看出，四种数据代表的求法不同，所表示的意义也各异。

平均数是所有数据之和除以数据的个数所得的商，它是分析和比较数据的集中趋势时最常用的数据代表。平均数的计算利用了一组数据中的每一个数据。任何一个数据的变化。都会影响平均数的大小。如果一组数据中有少数数据的值明显地过大或过小，最好不要仅仅使用平均数来考量，因为个别过大或过小的极端值会导致平均数与数据的实际集中点有较大差距。这时，最好用中位数作为数据代表，因为中位数不受极端值的影响。有时，为了决定是用平均数还是用中位数作为代表来分析一组数据的集中趋势，最好把这两个数据代表都算出来。如果它们的值很接近，则使用平均数；如果它们有很大的不同，则使用中位数。

根据一组数据的中位数，可以把数据分成同等数目的两组，其中一组数据的值不小于中位数，而另一组数据的值不大于中位数。将一组数据由小到大排列，有奇数个数据时，处于正中间位置的数就是中位数：有偶数个数据时，取处于正中间位置的两个数的平均数作为中位数。可以看出，中位数并不一定是原始数据之一。但它很好地代表了一组数据的“中点”，而且很容易找出它。

众数是指一组数据中出现次数最多的数据。它一定是这组数据中的某个数据。有时，众数可能不止一个。如上例中乙的训练成绩就有两个众数。如果一组数据中各个不同的数值出现的次数完全一样，则这组数据就没有众数。找众数只需要比较各数据的个数，而不需要计算。众数反映了一组数据的最大集中点。由众数可知这个数据在这组数据中出现的次数最多，但由它并不能知道这个数据具体出现了多少次，以及它比其他数据的出现次数多到何种程度。和中位数一样，众数也不受极端值的影响。

平均数、中位数和众数的侧重点不同，反映一组数据的集中趋势的角度不同。因此，应根据实际问题的需要，选取合适的数据代表来研究数据的集中趋势。

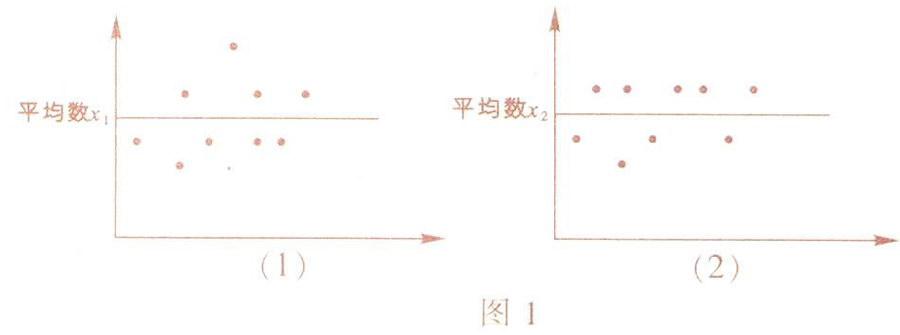
从方差的计算公式可以看出。它实际上是各数据与平均数之差的平方的平均数。之所以用差的平方，是因为差本身有正负。而平方后则不存在负数，相加求平均数时不会正负相抵，从而能更准确地刻画各数据与平均数的平均偏离程度。图1是数据散点图。其中（1）（2）里的点分别表示两组数据。直观上可以发现，（1）中数据点分布的离散程度较高，各点与平均数对应的水平线的偏离度大；（2）中数据点分布的离散程度较低，各点与平均数对应的水平线的偏离度小。这里的偏离度不是就个别数据点而论的。而是就所有数据点的偏离度的平均水平而言的。（1）中数据的方差较大，（2）中数据的方差较小。这是数据离散程度的几何解释。