建筑物垂直度监测及精度分析

韦小娜，李齐键，帖黎阳，刘丁，马宇滕

（合肥工业大学土木与水利工程学院，安徽 合肥 230601）



建筑物垂直度监测及精度分析

韦小娜，李齐键，帖黎阳，刘丁，马宇滕

（合肥工业大学土木与水利工程学院，安徽 合肥 230601）

目前建筑物变形监测，由传统的单一监测手段向点、线、面立体交叉的空间模式发展。传统建筑物垂直度的观测是点对点的，文章采用面对面的方法，即观察曲面的变形情况来确定建筑物变形。然后用全站仪测量高层建筑物得出的数据进行精度分析与观察，运用软件处理数据，分析精度，能够改善测量人员对建筑物的垂直度监测及精度分析工作，提高生产生活效率，所提到的用最小二乘法拟合曲面方程，与用最小二乘法拟合曲线的方法类似，但曲面拟合的计算过程比曲线拟合的计算过程麻烦得多、复杂得多。

变形监测；全站仪；自动化；最小二乘法；曲面方程；拟合；二次曲面；精度分析

1　概述

对于快速发展的城市，必然有越来越多的高层建筑物和超高层建筑物，常见的为框架结构外面安装玻璃幕墙，那么玻璃幕墙的安全性体现地越来越重要，或者由于种种原因建筑物产生变形，而高层建筑物的倾斜对建筑物的危害较大，对建筑物的使用寿命有直接的影响。需要对建筑物进行倾斜观测，以便及时掌握建筑物的安全状况，及时发现问题并予以解决，从而保护人民与财产安全。所以，有必要对建筑物的倾斜观测进行探讨。所谓倾斜，即建筑物顶部及底部中心不在一条垂直线上，倾斜率就是顶底中心水平投影距与建筑物高度之比。目前对建筑物倾斜的测试手段有测斜系统、全站仪等。虽然用测斜系统测量倾斜精度较高，但是测斜管的埋设及测试工作有比较大的困难，而且费用高。由于全站仪在工程建设中应用十分广泛，而用全站仪进行建筑物倾斜测量，测点的埋设容易，测量方便灵活。

2　监测方案的实施

选取合肥工业大学校内逸夫楼北侧玻璃幕墙为观测面。《高层建筑混凝土结构技术规程》（JGJ 3—2002）对高层建筑结构施工的测量放线作业及其允许误差作了明确的规定。其中第7．2．3条，规定了测量竖向垂直度时，必须根据建筑平面布置的具体情况确定若干竖向控制轴线，并应由初始控制线向上投测。对于轴线投测的误差，规定了层间测量偏差不应超过3mm；建筑全高垂直度测量偏差不应超过3H/10000（H为建筑总高度），且对应于不同高度范围的建筑物，其总高轴线投测偏差有不同的规定。使用具有反射片代替反光镜功能的全站仪进行垂直度监测的示意图见图1。在监测前，先在欲监测的柱体上布点并贴上反光片。布点时应注意：视建筑物实际情况布设足够的监测点，上部点和对应的下部点布设在同一柱体上，所布监测点应能反映出建筑整体的垂直度误差情况。对于逸夫楼北侧玻璃幕墙我们布设了20个点，其中10个点拟合平面，另外10个点分析精度。布点完成后，在距建筑物100～150m的地面上合适位置O处架设TS30全站仪，精确整平后，即可以同一个任意后视方向依次测出墙面上各反光片点的坐标。

根据上述理论对合肥工业大学校内逸夫楼进行合理安排实测，在2、3、5、7、9楼安置徕卡反光片（60mm×60mm），如下示意图。

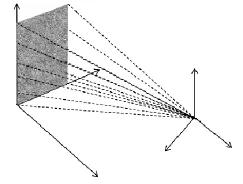
图1

3　数据处理

3.1高次曲面方程拟合的最小二乘法

这里Q可看作是关于ai的函数，共有10个未知量ai，所以上述拟合多项式的构造问题可以归结为求多元函数的极值问题，即ai应满足。

于是可得：

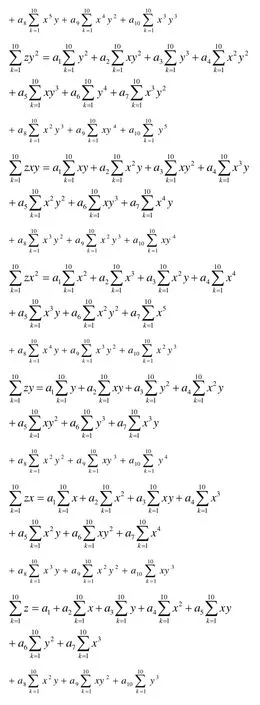
10个离散数据点的坐标值　表1

在计算机上应用matlab系统中的高斯法可计算出结果：

所以拟合出来的曲面方程为：

z=0.01724+1201.1556x-6328.1033941788y +1.8785x2+13767.5394xy+0.01194y2-7244.787x3+5701.0081x2y-7347.9873xy2-1.053648y3

在计算机上应用matlab系统中的命令作出这个三次曲面图

>>x=0：0.01：1;y=0：0.01：1;

>>[X，Y]=meshgrid（x，y）;

>>Z=0.01724+1201.1556.*X-6328.10339.*Y+1.87 85.*X.*X+13767.5394.*X.*Y+0.01194.*Y.*Y-7244.78 7.*X.*X.*X+5701.0081.*X.*X.*Y-7347.9873.*X.*Y.* Y-1.053648.*Y.*Y.*Y;

>>mesh（X，Y，Z）;title（'拟合出来的三次曲面图'）;

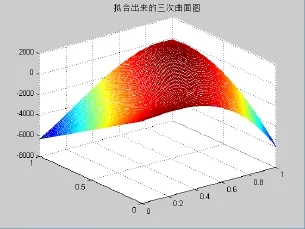
图2

4　结论

通过高精度的全站仪利用反光片代替棱镜，测量高层建筑物上点的X、Y、Z坐标，利用采集的实测点坐标数据拟合出平面，通过该面与垂直面的角度，得到高层建筑物的垂直度。传统的建筑物主体的垂直度观测应测定建筑顶部观测点相对于底部固定点或上层相当于下层观测点的倾斜度。而我们是通过测量许多建筑物外部观测点，拟合出面求建筑物垂直度，在理论上，这种方法比传统方法精度更高、更准确，这是我们测量建筑物变形的一个方法创新。应用最小二乘法拟合曲面方程，数据的计算工作量大，计算过程复杂。实践证明，如果我们的垂直度观测新方法能够更加完善，那么对于当前高层建筑物的垂直度观测来说，开辟了新思维，而且将是一个很实用、很简便，又能保证测量精度的一种测量方法。通过拟合面求建筑物垂直度对建筑物进行倾斜观测，及时掌握建筑物的安全状况，及时发现问题并予以解决，对保护人民与财产安全将有重大意义。

[1]JGJ8-2007，建筑变形测量规程[S].

[2]GB50026-93，工程测量规范[S].

[3]JGJ3-2002，高层建筑混凝土结构技术规程[S].

[4]胡伍生，潘庆林.土木工程测量[M].南京：东南大学出版社，2012.

[5]刘进山，李小平.MATLAB平台上几种线性方程组解法的比较[J].科技信息，2007（19）.

[6]霍晓程，李小平.用最小二乘法拟合曲面方程[J].赤峰学院学报，2009 （25）.

[7]董春来.MATLAB语言及测绘数据处理应用[M].成都：西南交通大学出版社，2012.

TU198

A

1007-7359(2016)03-0257-03

10.16330/j.cnki.1007-7359.2016.03.094

合肥工业大学2014年国家级大学生创新训练计划项目（编号：201410359029）。

韦小娜（1994-），女，安徽阜阳人，合肥工业大学土木与水利工程学院本科在读，专业：测绘工程。