乙二醇溶液水平新型多头内螺纹管内流阻特性

张吉礼，王永辉，马志先，陈敬东

（大连理工大学土木学院，辽宁 大连 116024）



乙二醇溶液水平新型多头内螺纹管内流阻特性

张吉礼，王永辉，马志先，陈敬东

（大连理工大学土木学院，辽宁 大连 116024）

建立了水平管内绝热流动阻力特性试验系统，试验研究了乙二醇溶液在两种新型多头内螺纹管内的流动特性。试验中，乙二醇体积分数为15%，两种试验管公称内径为22 mm与16 mm、螺纹头数为60头与38头、螺旋升角为45°与60°、相对粗糙高为0.022与0.053，测试段长度分别为2643 mm与2945 mm，Pr范围13.9～23.2，Re范围4000～33000。结果表明：多头内螺纹管阻力系数达到极大值之前的变化趋势与均匀粗糙管显著不同，而且无法通过既有多头内螺纹管经验模型准确描述；多头内螺纹管内达到阻力系数极大值的分界点Re为内肋结构参数的函数；入口效应对内螺纹管阻力系数的影响随Re增加而增大，传统的判别入口段可忽略的判据（l/di＞60）并不适用于多头内螺纹管，尤其是在Re＞20000的工况；既有多头内螺纹管经验模型适用工况条件有待进一步拓宽，多头内螺纹结构流动阻力的作用机制、阻力系数出现极大值的分界点的变化规律有待进一步试验探索。

内螺纹管；阻力系数；乙二醇；入口效应；试验；流动；模拟；数值分析

引　言

通过强化传热手段降低两器（制冷循环中的蒸发器与冷凝器）传热温差是提升制冷循环效率的有效手段之一，带有内螺纹肋结构的双侧强化管广泛用于壳管式蒸发器与冷凝器，该类换热管管内阻力系数是应用其进行两器设计开发的必备参数。然而，新的内螺纹肋结构与介质组合下的管内流动换热问题仍依赖于试验求解，尽管前人已在内螺纹管管内流动换热问题的试验与理论研究方面付出了极大的努力。

试验方面，Wang等［1］、张定才等［2］、Li等［3］、Siddique等［4］、Filho等［5］、Raj等［6］、Copetti等［7］与Naphon等［8］以水、R11、乙二醇与过冷R134a等为介质试验研究了多种内螺纹管在不同Re区间的摩阻特征，并基于试验结果分析探讨了肋高、肋间距、螺纹头数、管径、螺旋升角等因素对阻力系数的影响，结果一致表明：Re＞10000后内螺纹管阻力系数高于光管，Re＞30000后内螺纹管阻力系数变化趋势与光管趋同（阻力系数随Re增大而减小），阻力系数随肋高与螺纹头数增加而增大。但不同研究者获得的研究成果亦有相悖之处，如部分学者得出整个Re区间内阻力系数随Re变化趋势均与光管相一致，部分学者得出Re＜10000时内螺纹管阻力系数与光管相近、Re＞10000时内螺纹管阻力系数大于光管，部分学者得出3300≤Re≤22500范围内螺纹管阻力系数为Blasius公式计算值的2倍，其中缘由值得探究。而为众多研究者沿用的作为光管内旺盛湍流的分界点（Re=10000）是否可用于内螺纹管，普遍缺乏必要的论证。

理论分析方面，Webb等［9］、Han等［10］、Cheng等［11］、洪荣华等［12］、Zdaniuk等［13-15］、Meyer等［16］、Celen等［17］基于试验结果的理论分析、试验结果与前人提出的经验方程的对比分析相继给出适用于不同内螺纹肋结构与Re区间阻力系数经验方程，Ağra等［18］在Zdaniuk等［13-15］工作基础上结合数值试验进一步研究了12000≤Re≤54000范围内多头内螺纹管内的静压分布特征。与传统的阻力系数模型相比，以Zdaniuk等［13］模型为代表的半经验模型已经较全面地考虑了螺纹头数、螺旋升角、相对粗糙高（肋高/管内径）与Re等因素的影响，但各模型适用的工况区间（各因素的范围）有待进一步拓宽。此外，各模型在忽略入口效应对内螺纹管阻力系数影响时亦缺乏必要的论证。

前人在内螺纹管阻力系数试验与理论研究方面的研究成果已为该类换热管的推广应用做出了巨大的贡献，也为进一步试验研究新型结构内螺纹管摩阻特征、提出更精确与普适的阻力系数模型奠定了良好的基础。本研究在前人工作基础上，结合乙二醇溶液在两种新型结构内螺纹管内的流阻特征试验与理论分析探讨内螺纹管对应旺盛湍流分界点问题与入口段问题，并进一步结合试验结果与Zdaniuk等［13］模型及Nikuradse［19］实验结果的对比分析探讨多头内螺纹管阻力系数模型的发展方向以及多头内螺纹结构与均匀粗糙结构对管内阻力系数影响差异的根源。本研究结果可直接用于两种新型内螺纹结构换热管的推广应用，间接为日后研究入口段与旺盛湍流分界点等问题，完善内螺纹管阻力系数模型提供参考。

1　试　验

以获取乙二醇溶液在水平强化管内流动与换热特性及入口效应影响为目标设计建立了乙二醇溶液水平管内流动与换热试验平台，本研究试验与该系统中的流阻测试部分对应，以下简介试验详情。

1.1试验系统

乙二醇溶液水平管内流动阻力系数测试系统原理如图1所示，该系统由溶液循环、溶液冷却循环、计算机监控与数据采集等子系统构成。

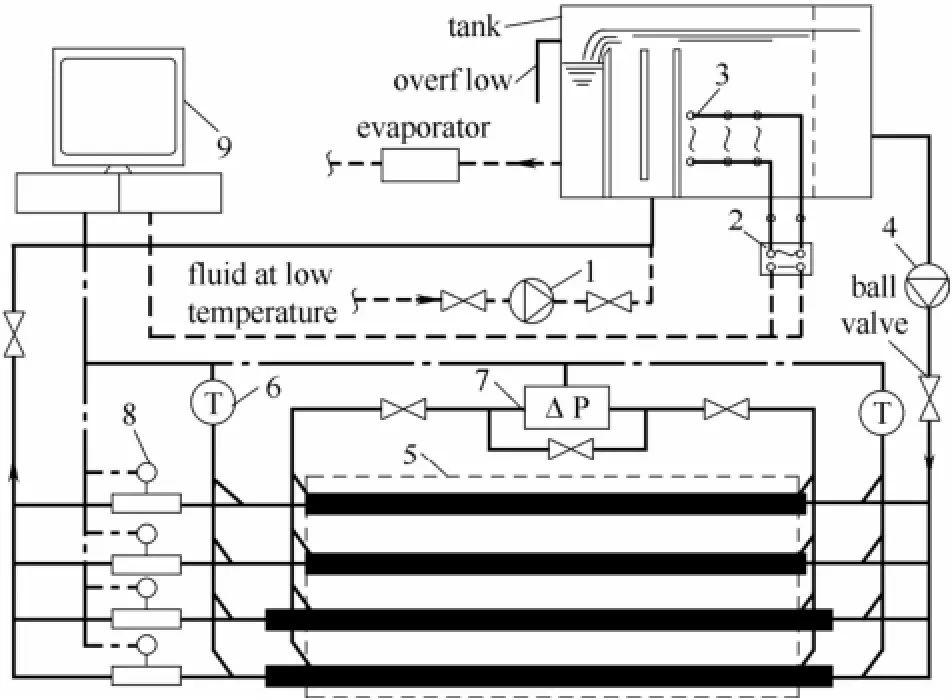
图1　试验系统原理Fig.1　Schematic diagram of test system 1，4—working fluid pump；2—silicon controlled switch；3—electric heater；5—test section；6—PT-100 temperature sensor；7—differential pressure transducer；8—turbine flowmeter；9—computer measurement and control system

（1）溶液循环具备稳定压力与温度（设定温度）的乙二醇溶液由高位水箱出水腔经由循环泵4输送到试验段5，流经试验管及其后的涡轮流量计8后与来自溶液冷却循环的低温溶液混合后进入水箱回水腔，与水箱内溶液混合后进入水箱再热腔，经再热腔内置的电加热器加热到设定温度后再次进入高位水箱出水腔，周而复始，形成具有高水力与热力稳定性的溶液循环。

（2）溶液冷却循环溢流腔内溶液经溶液泵泵送至溶液冷却器（制冷机蒸发器），降温后经电加热器再热至冷却溶液设定温度（低于溶液循环设定温度）后进入水箱回水总管与溶液循环回水混合，混合后溶液循环过程与（1）中对应部分一致。

（3）计算机监控与数据采集系统试验中采用量程0.6～6 m3·h-1、精度等级0.5级的涡轮流量计测量溶液循环流量，试验前、后利用称重法对各流量计的低量程读值（0.6～2.5 m3·h-1）进行校准（标定间隔0.25 m3·h-1）；采用精度等级0.1级，量程为0～10 kPa、0～20 kPa、0～40 kPa、0～60 kPa与0～100 kPa的5台压差变送器并联构成的压差表组测量试验管两端的压差，试验前通过标准液柱差高校准各表在低量程范围内的读值（标定间隔20 cm水柱高）；采用四线制PT-100温度传感器（温度测试精度优于±0.02℃）监测试验管进、出口溶液温度与温差（进、出口温度传感器读值之差），试验前采用一等标准水银温度计与分辨率为0.001℃的精密恒温水槽标定各温度传感器；采用变设定值的模糊PID控制方法，实现溶液循环温度与设定温度偏差始终控制在±0.1℃范围之内；采用配备7708板卡的Keithley2700数据采集器（RS232接口连接到计算机），以30 s为采集周期对每个试验点进行16次重复采样（单次采样利用采集器中的平均值滤波方法提高精度），采样获得数据实时传输到计算机处理与储存。

1.2试验段

试验段中试验管安装如图2所示，图中l、lo分别为试验管总长与测试段长度（表1），试验管整体外被30mm厚的橡塑保温材料（保温层厚度根据管内溶液平均温度、环境温度与管内溶液允许温升0.1℃计算得出）；试验管进、出口各安装一只四线制铂电阻温度传感器监测溶液进、出口温度，传感器探头均迎着来流方向安装；试验管内溶液流量通过装设在管路上的球阀调节；试验管上开设直径为0.5 mm的孔（先装引压管后再开孔并去开孔在内壁形成的毛刺），进、出口两端的引压管分别接压差传感器表组的H与L接口。

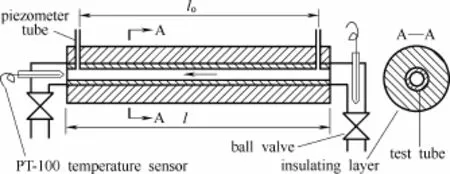
图2　试验段Fig.2　Test section

1.3试验管

图3　试验管Fig.3　Tubes tested

试验用管的几何参数见表1，其中Tube-s为光管，其余为多头内螺纹粗糙管（管内结构如图3所示），Ns为螺纹头数、p为肋间距、e为内肋高、α为螺旋升角、di为管内径、θ为肋顶角、s为肋基间距、l为管总长、lo为试验段长度，各量单位见表1。

表1　R试验管结构参数Table 1　Geometric parameters of test tube

1.4试验工况与工质

（1）试验工况参见表2，表中Ti为试验管进口溶液温度，测试中进口溶液温度达到设定温度后通过调节溶液流量实现各测点对应工况。

基于数量级比较略去微小量δdi/di、δρ/ρ及δlo/lo3项后，结合试验工况（试验中压差、流量与温度等）与仪器仪表测试精度可推算出阻力系数的极大试验相对误差为±2.4%（其中各测试量随机误差均按3σ取值）。

1.6试验系统可靠性

（1）绝热工况验证试验管不同入口温度进、出口温升试验结果如图4所示。图示结果表明，试验管外被保温材料后介质流经试验管的温升均小于0.05℃，满足设计温升低于0.1℃的要求。

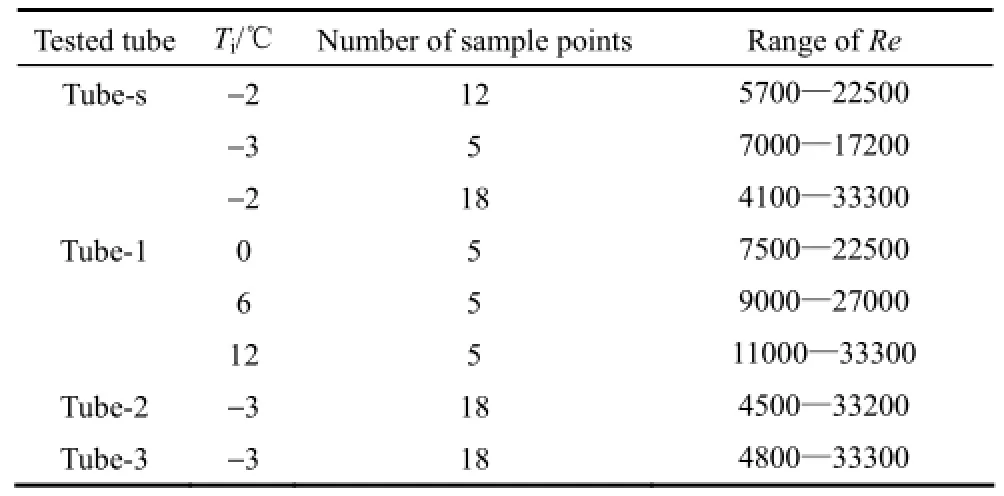
表2　R试验工况Table 2　Test conditions

（2）试验工质体积分数为15%的乙二醇溶液，采用纯净自来水（用3层高效滤布循环过滤5次）与纯乙二醇（99.5%）以体积比3：17配制。试验工况范围内试验工质的Pr范围为13.9～23.2。

1.5试验数据处理

（1）数据处理试验目标为获得阻力系数f与量纲1数Re的关系。

阻力系数f的试验原理方程如下

图4　试验管进、出口温升Fig.4　Temperature rise between import and export of tube tested

式中，Δp为试验管两端压力差，kPa；di为试验管内径，m；ρ为工质密度，kg·m-3；lo为试验段长度，m；u为工质流速，m·s-1。

Re的计算表达式如下

式中，μ为流体动力黏度，Pa·s。

（2）误差分析根据式（1）与误差分析原理［20］可得阻力系数f相对误差计算公式

（2）标模试验检验试验系统获取的光管管内阻力系数结果与Filonenko公式［21］［式（4）］计算值对比如图5（a）所示，图中试验值与公式计算值的相对偏差见图5（b），可见试验值与公式计算值相对偏差均在±2%之内，表明试验系统具有较高的可靠性。

2　试验结果

2.1介质温度对内螺纹管阻力系数的影响

溶液入口温度对多头内螺纹管阻力系数的影响随溶液Re的变化如图6所示，图中实线为试验结果的回归曲线，虚线为与该曲线相对偏差为±2.4%的曲线。图示结果表明，不同入口溶液温度对应试验结果与中位值回归曲线的偏差大都（95%以上）在极大试验相对误差±2.4%限值范围内，因此可判定溶液在管内的阻力系数为Re的单一函数，而且溶液温度所致其他物性参数变化对阻力系数的影响均可忽略不计。

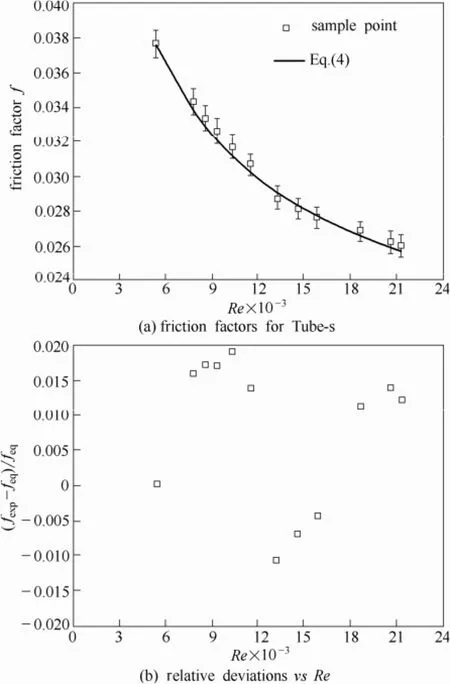
图5　Tube-s试验结果与理论公式计算值比较Fig.5　Comparison between experimental results and that calculated by Filonenko formula

图6　溶液入口温度对Tube-1管内阻力系数影响随Re的变化Fig.6　Effect of solution inlet temperature on friction factor vs Reynolds number

2.2阻力系数随Re的变化

乙二醇溶液在多头内螺纹管管内的阻力系数试验结果与Re的对应关系如图7所示，图中Tube-s对应阻力系数结果为Filonenko公式［21］［式（4）］计算值。

图7　试验管阻力系数随Re的变化Fig.7　Friction factors of test tubes vs Reynolds number

图示结果表明试验Re区间内多头内螺纹管阻力系数的变化趋势与光管具有显著差异。其中Tube-1（内径16.662 mm、38头三角螺纹内肋，具体参数见表1）在Re为11000附近出现一个驻点（亦是极大值点，记为Recr，1#），驻点前f随Re增大而增大且无拐点，驻点后f随Re增大而减小；Tube-2与Tube-3（内径22.48 mm、60头梯形螺纹内肋，具体参数见表1）在Re为7500与17000附近均出现驻点（亦是极值点），第一驻点前f随Re升高而降低，两个驻点之间f随Re增大而增大且存在一拐点，第二驻点（Recr，2#）后f随Re增大而减小（但在试验Re范围内第二驻点后未见拐点）；Tube-s（光管，粗糙度小于0.8 μm）f随Re增大而减小且与理论公式计算值变化趋势相一致。

对于光管（或均匀粗糙管），通常将Re=10000作为旺盛紊流的分界点（记为Recr），当Re＞Recr时可认定f随Re单调变化，相应地可运用紊流区间的阻力系数经验方程较准确地预测阻力系数的变化趋势乃至数值（图5）；但对于多头内螺纹管，如果仍将Recr取为10000，则在Re＞Recr后不能保证f随Re单调变化（图7）。此外，由图7所示结果可知不同结构的多头内螺纹管的Recr显著不同。

2.3入口效应对多头内螺纹管阻力系数的影响

对于不同长度同型（除长度外其余几何参数全同）换热管，入口段对阻力系数影响的比重不同，因此本研究试验中利用不同长度的同型换热管（Tube-2与Tube-3）的阻力系数的对比分析考察入口效应的影响。为便于计算，首先利用5次多项式（根据回归效果试探选出）对试验结果进行回归分析，得出两试验管阻力系数的计算公式，公式适用Re范围为4500～33000，而且范围不可扩展。公式计算值（f）与试验结果（fexp）的相对偏差［（f-fexp）/fexp］如图8所示，图示结果表明实验值与公式计算值偏差均在±2.0%之内。

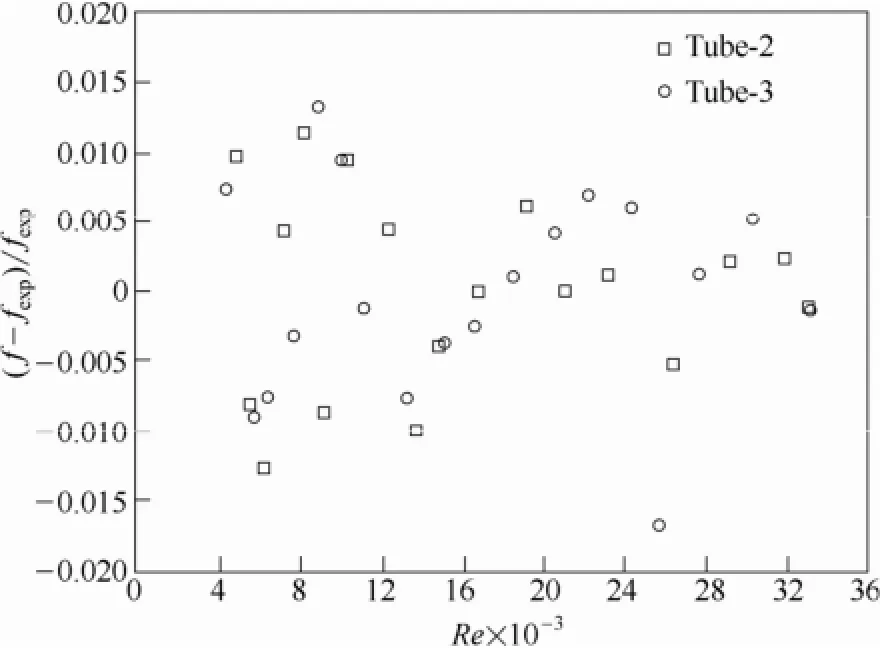
图8　Tube-2与Tube-3阻力系数拟合偏差Fig.8　Fitting deviations of Tube-2 and Tube-3

其次，利用两管的阻力系数公式计算出同Re下两管阻力系数的相对偏差［（f2-f3）/f3］。对应结果如图9所示，图示结果表明，同Re下Tube-2（测试段长2.643 m）阻力系数均高于Tube-3（测试段长2.945 m），Re由4500递增至33000过程对应阻力系数相对偏差从3.4%递增至8.5%。综上可知，对于多头内螺纹管，入口段影响体现在增大阻力系数且其影响随Re增加而增大，长径比接近120时（Tube-2长径比lo/di=2643/22.48≈118）仍不能忽略入口效应影响，尤其是在Re＞20000的工况。

图9　Tube-2与Tube-3阻力系数相对偏差Fig.9　Relative deviations between friction factors of Tube-2 and Tube-3

3　讨　论

3.1试验结果与经典模型对比分析

试验结果与Zdaniuk等［13］得到的多头内螺纹管阻力系数模型［式（5）］预测值的比较如图10所示。

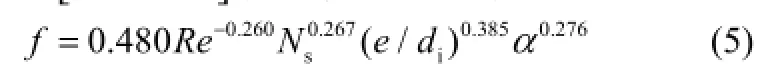
式中各参数及其覆盖范围：螺旋升角α范围25°～48°，螺纹头数Ns范围10～45，肋高与内径比e/di范围为0.0199～0.0327，Re范围12000～60000。

图10　试验结果与经典模型预测值比较Fig.10　Comparison of friction factors between experimental result and that predicted by semi-empirical model

图示结果表明，式（5）预测值随Re增大而单调递减。Re低于11000时，因预测值与试验曲线的变化趋势相反，二者偏差随Re降低而迅速增加；Re超过12000后，预测值与Tube-1试验结果偏差大都在±20%范围之外，而且偏差持续为负值，Tube-1 α和e/di超出式（5）适用范围是恒定偏差的成因之一；Re在12000～17000之间，预测值与Tube-2和Tube-3实验值之间的偏差不断减小；Re超过17000后，预测值与Tube-2和Tube-3实验结果偏差在-20%左右，Tube-2和Tube-3 Ns超出式（5）适用范围。因此可推测，该模型用于高肋密度多头内螺纹管时应缩小式中Ns和e/di指数的数值。图示预测值与试验结果偏差随Re的变化如图11所示。

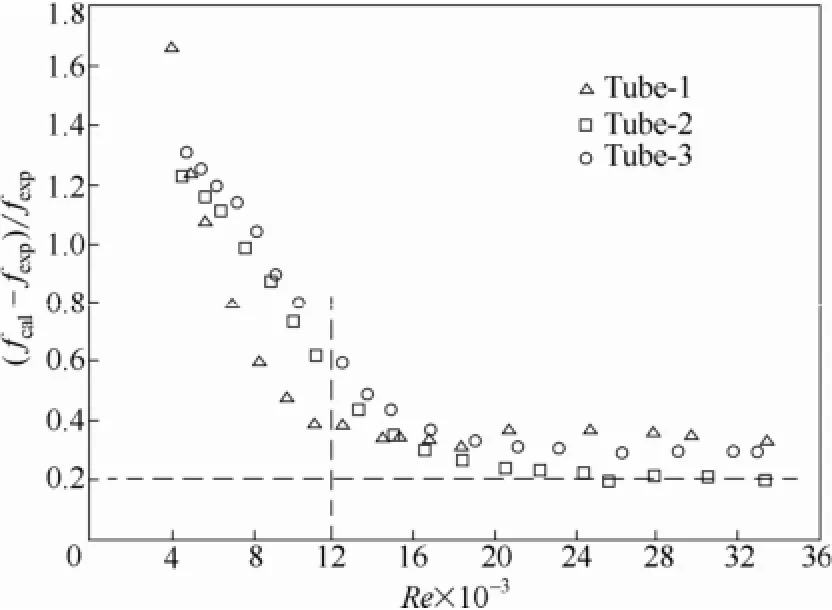
图11　试验结果与经典模型预测值相对偏差Fig 11　Relative deviations between experimental results and that predicted by semi-empirical model

综上所述，既有多头内螺纹管阻力系数经验模型的适用管型参数范围（螺纹头数、螺旋升角等）有待进一步拓宽，而在阻力系数达到极大值之前所对应的Re区间需要补充适宜的阻力系数经验模型，以覆盖该类换热管在低温与高黏流体的使用工况（如使用乙二醇溶液的蓄冷工况）。

3.2多头螺纹与均匀粗糙对阻力系数影响的差异

Nikuradse［19］试验中采用均匀粗糙管，管内粗糙为类球状均匀砂粒，其在湍流区域的阻力系数随Re的变化曲线如图12所示（根据文献［19］中数据绘制）。图中曲线ab为紊流光滑区，该区内f只与Re有关；曲线ab与曲线cd之间为紊流过渡区，曲线为波状曲线；曲线cd右侧为紊流粗糙区，f仅为相对粗糙度（ks/di）的函数。

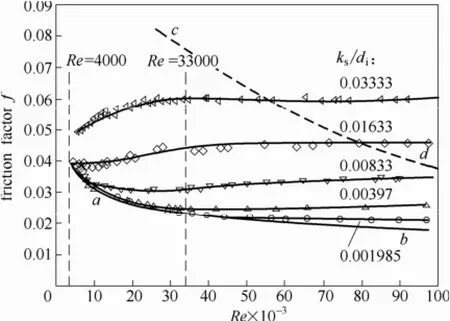
图12　Nikuradse试验部分紊流曲线Fig.12　Nikuradse's experimental results in turbulence zone

图13　多头内螺纹管阻力系数与Nikuradse试验结果对比Fig.13　Comparison between Nikuradse's experimental results and current experimental results

以肋高与内径比（e/di）表征多头内螺纹管的相对粗糙度［13］，即可将试验结果同Nikuradse试验曲线进行比较（图13）。由图13所示结果可知：① e/di与ks/di值相近时，多头内螺纹管阻力系数明显高于Nikuradse试验中使用的均匀粗糙管的阻力系数，而且前者随Re的变化趋势亦与后者显著不同。例如，Re由4000增至33000的过程中，Tube-1管阻力系数存在先增后降的剧烈变化，但粗糙度略低于该管的均匀粗糙管的阻力系数单调递增且增长率随Re增大而减小。② 当Re超过20000之后，随着Re的增大，多头内螺纹管阻力系数试验结果以递减方式向均匀粗糙管结果逼近，而该区均匀粗糙管阻力系数结果随Re单调递增。③ 多头内螺纹管阻力系数值随e/di增加而增大，但不同内螺纹结构对应阻力系数的变化趋势相异，这与均匀粗糙对应情况相似。综上，基于Nikuradse试验获得的阻力系数准则方程不适合用于预测内螺纹管在紊流过渡区内的阻力系数，尤其在Re较小时二者差别显著。

Re较低时，流体流过内螺纹结构产生的摩擦阻力与压差阻力会诱导近壁面流体以旋转方式前进。流体以旋转方式前进一方面会提高流型的稳定性，使层流向临界过渡区、临界过渡区向紊流光滑区转化的临界Re延后，导致Tube-2与Tube-3试验管层流与临界过渡区之间的临界点对应的Re延至6000左右（在Re为4000～6000时仍呈现出Nikuradse实验层流区阻力系数的变化趋势）、临界过渡区与紊流光滑区之间的临界点对应的Re延后至17000左右（Re为6000～17000区间体现出Nikuradse实验层流向紊流过渡区阻力系数的变化趋势）、Tube-1试验管过渡区与紊流的临界点对应的Re延后至12000左右，另一方面会使近壁面流体在管内的实际行程较均匀粗糙管大幅度增加，进而导致内螺纹管阻力系数的表观值（以管内平均流速与内径计算得出Re对应的阻力系数值）大幅度增加（流体旋进时在管轴线上的分速度的均值与流体非旋进时相同，因此其旋进速度必超过轴向速度，高流速与加长行程的摩擦损失折算到短行程，进而导致阻力系数大幅度增加）。

Re高于紊流过渡区对应临界值后，随着近壁区流体轴向速度的增大，内螺纹结构诱发管内流体旋进的能力与流体旋进维持流型稳定性的能力逐步被削弱，流体旋进所致阻力系数增大的效应随之减弱，相应地，内螺纹管阻力系数随Re增加而降低并逐步向同粗糙度的均匀粗糙管的阻力系数值逼近。

综上所述，内螺纹管阻力系数达到最大值之后，可采用既有经典内螺纹管阻力系数模型预测阻力系数值，但阻力系数的最大值仍依赖于试验求解（尚无可靠预测方法）；在阻力系数达到最大值之前，内螺纹管阻力系数的变化趋势显著偏离既有经典模型预测情况，而且目前尚无可靠方法预测。

4　结　论

通过本研究工作可得如下结论。

（1）光管试验结果能与Filonenko公式计算结果较好地吻合，而且溶液温度对试验结果没有影响。

（2）多头内螺纹管内流体流动状态转变对应的Re区间较光管发生显著变化，致使4000＜Re＜Recr区间内螺纹管阻力系数的变化趋势与均匀粗糙管阻力系数的变化趋势截然不同；内螺纹管阻力系数在Re=Recr时达到极大值，Recr是多头内螺纹管内肋结构参数的函数；传统的用于判定均匀粗糙管内流态转变的准则不应无条件用于内螺纹管内的流态判定。

（3）入口效应对内螺纹管阻力系数的影响随Re增加而增大，传统的判别入口段可忽略的判据（l/di＞60）并不适用于多头内螺纹管，尤其是在Re＞20000的工况。

符 号 说 明

di——管内径，mm

do——管外径，mm

e ——内肋高，mm

f ——阻力系数

l ——管总长，mm

lo——管试验段长度，mm

Ns——内肋螺纹头数

Pr——Prandtl数

p——肋间距，mm

Δp——流体压力损失，kPa

Re——Reynolds数

Recr——阻力系数最大值时Reynolds数

s——肋基间距，mm

Ti——流体入口温度，℃

u——溶液流速，m·s-1

α——螺旋升角，（°）

θ——肋顶角，（°）

μ——流体动力黏度，Pa·s

ρ——流体密度，kg·m-3

References

［1］ WANG H S， ROSE J W. Prediction of effective friction factors for single-phase flow in horizontal microfin tubes ［J］. International Journal of Refrigeration， 2004， 27（8）： 904-913. DOI： 10.1016/j. ijrefrig.2004.04.013.

［2］ 张定才， 何雅玲， 刘启斌， 等. 内螺旋肋管流动与传热特性的实验研究 ［J］. 工程热物理学报， 2006， 27（6）： 1029-1031. ZHANG D C， HE Y L， LIU Q B， et al. Experimental study of fluid flow and heat transfer in internal helical-rib tubes ［J］. Journal of Engineering Thermophysics， 2006， 27（6）： 1029-1031.

［3］ LI X W， MENG J A， LI Z X. Experimental study of single-phase pressure drop and heat transfer in a micro-fin tube ［J］. Experimental Thermal and Fluid Science， 2007， 32（2）： 641-648. DOI： 10.1016/j. expthermflusci.2007.08.005.

［4］ SIDDIQUE M， ALHAZMY M. Experimental study of turbulent single-phase flow and heat transfer inside a micro-finned tube ［J］. International Journal of Refrigeration， 2008， 31（2）： 234-241. DOI：10.1016/j.ijrefrig.2007.06.005.

［5］ FILHO E P B， JABARDOB J M S. Experimental study of the thermal hydraulic performance of sub-cooled refrigerants flowing in smooth， micro-fin and herringbone tubes ［J］. Applied Thermal Engineering， 2014， 62（2）： 461-469. DOI： 10.1016/j.applthermaleng. 2013.10.002.

［6］ RAJ R， LAKSHMAN N S， MUKKAMALA Y. Single phase flow heat transfer and pressure drop measurements in doubly enhanced tubes ［J］. International Journal of Thermal Sciences， 2015，88：215-227. DOI： 10.1016/j.ijthermalsci.2014.10.004.

［7］ COPETTI J B， MACAGNAN M H， SOUZA D， et al. Experiments with micro-fin tube in single phase ［J］. International Journal of Refrigeration， 2004， 27（8）： 876-883. DOI： 10.1016/j.ijrefrig. 2004.04.015.

［8］ NAPHON P， SRIROMRULN P. Single-phase heat transfer and pressure drop in the micro-fin tubes with coiled wire insert ［J］. International Communications in Heat and Mass Transfer， 2006，33（2）： 176-183. DOI： 10.1016/j.icheatmasstransfer.2005.08.012

［9］ WEBB R L， NARAYANAMURTHY R， THORS P. Heat transfer and friction characteristics of internal helical-rib roughness ［J］. Journal of Heat Transfer-Transactions of the ASME， 2000， 122（1）： 134-142. DOI： 10.1115/1.521444.

［10］ HAN D H， LEE K J. Single-phase heat transfer and flow characteristics of micro-fin tubes ［J］. Applied Thermal Engineering，2005， 25（11/12）： 1657-1669. DOI： 10.1016/j.applthermaleng. 2004.10.015.

［11］ CHENG L X， CHEN T K. Study of single phase flow heat transfer and friction pressure drop in a spiral internally ribbed tube ［J］. Chemical Engineering & Technology. 2006， 29（5）： 588-595. DOI：10.1002/ceat.200600014.

［12］ 洪荣华， 钟昌雄， 倪煜， 等. 内螺纹强化管传热和阻力特性 ［J］.工程热物理学报， 2008， 29（1）： 154-156. HONG R H， ZHONG C X， NI Y， et al. Thermal analysis of heat transfer and friction coefficients for internal thread tubes ［J］. Journal of Engineering Thermophysics， 2008， 29（1）： 154-156

［13］ ZDANIUK G J， CHAMRA L M， WALTERS D K. Correlating heat transfer and friction in helically-finned tubes using artificial neural networks ［J］. International Journal of Heat and Mass Transfer， 2007，50（23/24）： 4713-4723. DOI： 10.1016/j.ijheatmasstransfer. 2007.03.043.

［14］ ZDANIUK G J， CHAMRA L M， MAGO P J. Experimental determination of heat transfer and friction in helically-finned tubes ［J］. Experimental Thermal and Fluid Science， 2008， 32（3）： 761-775. DOI：10.1016/j.expthermflusci.2007.09.006.

［15］ ZDANIUK G J， LUCK R， CHAMRA L M. Linear correlation of heat transfer and friction in helically-finned tubes using five simple groups of parameters ［J］. International Journal of Heat and Mass Transfer， 2008， 51（13/14）： 3548-3555. DOI： 10.1016/j.ijheatmasstransfer. 2007.10.022.

［16］ MEYER J P， OLIVIER J A. Transitional flow inside enhanced tubes for fully developed and developing flow with different types of inlet disturbances（Ⅰ）： Adiabatic pressure drops ［J］. International Journal of Heat and Mass Transfer， 2011， 54（7/8）： 1587-1597. DOI：10.1016/j.ijheatmasstransfer.2010.11.027.

［17］ CELEN A， DALKILIC A S， WONGWISES S. Experimental analysis of the single phase pressure drop characteristics of smooth and microfin tubes ［J］. International Communications in Heat and Mass Transfer， 2013， 46： 58-66. DOI： 10.1016/j.icheatmasstransfer. 2013.05.010.

［18］ AĞRA Ö， DEMIR H， ATAYILMAZ Ş Ö， et al. Numerical investigation of heat transfer and pressure drop in enhanced tubes ［J］. International Communications in Heat and Mass Transfer， 2011，38（10）： 1384-1391. DOI： 10.1016/j.icheatmasstransfer.2011.07.013.

［19］ NIKURADSE J. Laws of flow in rough pipes［R］. Washington： NACA TM 1292， 1950.

［20］ 费业泰. 误差理论与数据处理［M］. 6版. 北京： 机械工业出版社，2010： 62. FEI Y T. Theory of Errors and Data Processing ［M］. 6th ed. Beijing：China Machine Press， 2010： 62.

［21］ FILONENKO G K. Hydraulic resistance in pipes ［J］. Teploergetica，1954， 1（4）： 40-44.

Friction characteristics for water-ethylene glycol mixture flow in horizontal tubes with new type of helically fins

ZHANG Jili， WANG Yonghui， MA Zhixian， CHEN Jingdong
（School of Civil Engineering， Dalian University of Technology， Dalian 116024， Liaoning， China）

An experiment setup was built for investigating single-phase adiabatic flow characteristics of internal helical-rib roughness. The friction characteristics for 15% （by volume） water-ethylene glycol mixture flow in three internal finned tubes （two types of new developed internal helical-fins） and a smooth tube were obtained. The parameters of test tubes are nominal inside diameters （22 mm and 16 mm）， numbers of fins （60 and 38）， helix angles （45° and 60°） and fin height to inside diameter ratios （0.022 and 0.053）. The lengths of the internal helical-rib tubes in test section were 2643 mm and 2945 mm， respectively. The Prandtl number varied from 13.9 to 23.2 and the Reynolds number ranged from 4000 to 33000. The smooth-tube results were compared to the Filonenko equation with satisfactory agreement. The experimental results of different length and same type multi-start internal helically-finned tubes also showed that the entrance effect on the friction factor in the multi-start internal helically-finned tube increased with the increase of Re. Especially for Re＞20000， the criterion that entrance effect can be ignored when lo/di＞60 （lo—length in test section， di—inside diameter） was not suitable for the multi-start internal helically-finned tube. All the three helically-finned tubes results indicated that there was a critical Re， Recr， a function of geometric variables of internal helically fins. The friction factor achieved themaximum when Re=Recrand for 4000＜Re＜Recr. The earlier friction factor correlations could not be in good agreement with experimental data. Much efforts should be done to enlarge the application range of the earlier empirical formula. Also， for 4000＜Re＜Recr， the variation tendency of friction factors in multi-start internal helically-finned tubes were greatly different from those in equivalent roughness tubes used in the Nikuradse experiment. The difference between resistance mechanisms of internal helically-finned tube and artificial equivalent roughness tube was analyzed and deserved more attention.

date： 2015-10-08.

MA Zhixian， mazhixian@dlut.edu.cn

supported by the National Natural Science Foundation of China （51578102） and the Fundamental Research Funds for the Central Universities （DUT14ZD210， DUT15RC（4）24）.

internal helically-finned tube； friction factor； ethylene glycol； entrance effect； experiment； flow；simulation； numerical analysis

10.11949/j.issn.0438-1157.20151514

TK 124

A

0438—1157（2016）05—1762—09

2015-10-08收到初稿，2015-12-04收到修改稿。

联系人：马志先。第一作者：张吉礼（1969—），男，博士，教授。

国家自然科学基金项目（51578102）；中央高校基本科研业务费专项（DUT14ZD210， DUT15RC（4）24）。