水平圆形与方形微小通道内R134a冷凝数值模拟

2016-08-22张井志

化工学报 2016年5期

关键词：干度液膜方形

张井志，李　蔚

（1浙江大学能源工程学院，浙江杭州 310027；2先进航空发动机协同创新中心，浙江杭州 310027）

水平圆形与方形微小通道内R134a冷凝数值模拟

张井志1，2，李蔚1

（1浙江大学能源工程学院，浙江杭州 310027；2先进航空发动机协同创新中心，浙江杭州 310027）

利用数值模拟研究了水平圆形与方形微小通道内R134a的冷凝换热阻力特性，制冷剂饱和温度为320 K。结果表明：传热系数与摩擦压降梯度随着质量流量、干度的升高而升高，而干度大于0.85时，摩擦压降梯度随着干度的升高而降低。方形通道的换热与阻力均高于圆形通道，数值结果与文献冷凝换热、阻力公式吻合较好。圆形通道内冷凝液膜集聚在通道下部，而方形通道内液膜集中在角落区域。薄液膜区域所占的比例随着干度的增大而增大，方形通道内的液膜厚度要小于圆形通道，换热效果优于圆形通道。

凝结；微小通道；数值模拟；传热；压降

杨英英等［1］观测了内径2 mm水平圆管内R32冷凝流型，环形流区域随制冷剂流量的增大而增大。Illán-Gómez等［2］研究了微小通道（dh=1.16 mm）内R1234yf和R134a的冷凝换热过程，实验结果表明热导率、汽液密度比与汽液黏度比在冷凝换热过程中起着重要作用。Sakamatapan等［3］测定了微小通道内R134a的冷凝传热系数，指出传热系数随着干度、质量流量、壁面热流的增大而增大。Liu等［4］分析了圆形与方形通道（dh=1.152～0.952 mm）内R152a冷凝换热阻力特性，结果表明传热系数与压降随着饱和温度的升高而降低，方形通道的传热系数要优于圆形通道。

相比实验方法，数值计算可以获得内部流动情况，进而更详细地分析冷凝换热特性。Wang等［5-7］研究了微小通道内的冷凝换热，指出在方形和三角形通道内，表面张力的作用要强于重力及剪切力作用。Da Riva等［8-9］研究了水平光管内的冷凝流动，指出考虑液膜区域的湍流扰动可以更好吻合实验结果。刘纳等［10］研究了R32在水平微细管（dh=1 mm）内的冷凝，结果表明管顶部液膜厚度基本不变而底部液膜厚度逐渐变厚。El Mghari等［11］分析了微小方形通道内的冷凝换热情况，结果表明传热系数随水力直径的降低、壁面接触角及通道纵横比的增大而增大。

相对实验研究，微小通道内的冷凝换热数值模拟工作仍然处于起步阶段。前人针对冷凝的研究主要针对于换热特性，而对于阻力特性的研究仍有很大的不足。本研究主要对微小圆管与方形管内冷凝换热现象进行数值研究，讨论截面形状、质量流量、干度对其换热阻力特性的影响，并分析了圆管与方形管内冷凝换热时截面液膜厚度分布。

1　数值计算模型

汽液界面采用Ansys Fluent 14.5的VOF模型进行追踪。VOF模型质量守恒特性较好，并具有较高的界面精度，广泛应用于两相流数值模拟。采用SST k-ω湍流模型考虑汽、液两相的湍流运动。

1.1控制方程

计算区域流体控制方程如下：

连续性方程

动量方程

能量方程

体积分数方程

其中

式中，αl代表计算单元格内液体的体积分数，αl=1，代表单元格全为液体，αl=0代表单元格全为气体。

表面张力的作用采用Continuum Surface Force（CSF）模型考虑，其中动量方程中的体积力项F定义为

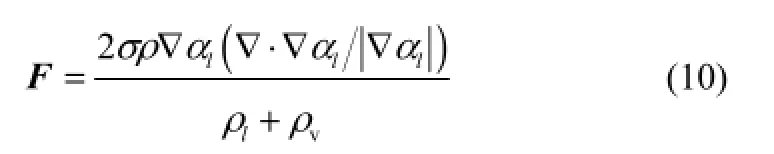
1.2汽液界面传热传质模型

对于相变换热的数值研究，关键点在于汽液界面传热传质问题。本研究采用Lee［12］模型考虑界面的传热传质情况，此模型广泛应用于冷凝［9-10］和沸腾［13-14］模拟。Lee［12］模型假设汽液界面温度为饱和温度，如式（11）所示，当汽相温度低于饱和温度或液相温度高于饱和温度时，界面产生质量与热量传递。由质量传递所引起的能量变化，通过能量方程中汽化潜热与质量传递之积考虑。

Da Riva等［9］指出过小的r系数会导致汽液界面的温度偏离饱和温度，而过高的r系数则会引起计算的收敛问题。相对而言，文献中对于蒸发、沸腾［13-14］的模拟，采用较小的r，而对于冷凝模拟则采用较大的r系数。本文模拟过程中r取值为1.5×106，其中汽液界面的温度与饱和温度之差小于0.5 K，传热传质模型利用Ansys Fluent中的用户自定义函数（UDF）实现。

1.3几何模型、边界条件及离散格式

采用三维模型分析圆形与方形通道内的冷凝情况，计算域如图1所示，计算域长度L设定为方形通道200 mm，圆形通道400 mm。方形通道（dh=1.57 mm）与圆形通道（dh=2 mm）的单位长度换热面积保持一致。考虑流动换热的对称性，采用1/2模型，YZ截面设定为对称边界条件。计算域入口设定为速度入口边界条件，出口设定为压力出口边界条件。管壁设定为无滑移的恒温壁面（T=310 K），流体饱和温度设定为320 K，制冷剂工质的物性采用REFPROP 8.0确定。

图1　计算模型Fig.1　Computational model

计算域采用结构化网格进行划分，壁面附近采用加强壁面函数考虑近壁区域液膜黏性底层的湍流，近壁面附近采用边界层网格，以满足壁面y+≈1.0。对网格进行无关性验证，对于圆形通道，网格数目为191.24万个及273.52万个时，壁面热流量的误差小于0.8%。考虑计算时间，最终圆形和方形通道的网格数目为191.24万个和173.33万个。

速度入口的速度分布、湍动能及湍流耗散利用长度为20 mm，截面网格分布与最终冷凝模拟模型一致的单相模拟获得，其中单相模拟采用周期性边界条件，以获得充分发展状态下入口值。入口温度设定为饱和温度320 K。

表1　R计算方法及离散格式Table 1　Solution method and discretization scheme

考虑模拟中重力与表面张力的计算，激活VOF模型中的隐式体积力选项，操作密度设定为汽相密度。由于采用相变模型，欠松弛因子设置为0.1～0.2，以提高计算稳定性，汽-液界面构造及其他参数的离散方法详见表1。

2　结果分析与讨论

2.1换热特性

图2为质量流量G为317、531、715 kg·m-2·s-1时，圆形与方形通道内冷凝传热系数随干度x的变化规律。由图2可得，传热系数随着质量流量、干度的增大而增大。在高干度（通道入口段附近）时，传热系数随干度的增大趋势要高于低干度时。在相同的质量流量与干度下，方形通道的传热系数高于圆形通道。相对圆形通道，方形通道内表面张力作用更强，促使液膜聚集在通道角落位置，导致在壁面其他位置液膜厚度大幅降低，换热热阻减小，换热效果提升。同时，在相同的换热面积下，方形通道的当量直径要低于圆管，较小的当量直径也是方形通道传热系数较高的一个原因。

图2　传热系数随干度与质量流量的变化Fig.2　Heat transfer coefficients vs vapor quality and mass flux

2.2阻力特性

对于相变换热，总的压降由摩擦压降、重力压降及加速压降构成。加速压降是由于进出口汽液含量变化而导致的压降损失，如式（13）所示。对于横管而言，重力压降可以忽略，则阻力压降梯度为总压降梯度与加速压降梯度之差，如式（14）所示。

图3为不同质量流量下，两通道内摩擦压降梯度随干度x的变化规律。由图3可得，摩擦压降随着质量流量的升高而升高，方形通道的压降损失要高于圆形通道，且二者之差随着质量流量的提高而增大。当x＜0.85时，摩擦压降随着x上升而上升，当x＞0.85时，摩擦压降随着x上升而逐渐降低。由于考虑液膜区域的湍流度，在入口段附近由于液膜Reynolds数相对较小，湍流度不强，导致进口段的压降稍低，Del Col等［15］的实验结果也得到类似现象。

图3　压降梯度随干度与质量流量的变化Fig.3　Pressure drop gradients vs vapor quality and mass flux

2.3模拟结果与经验公式对比

为验证数值模拟、相变传热传质模型及系数r选择的可靠性，将数值模拟所得到的传热系数及摩擦压降梯度与文献经验公式进行对比。采用平均绝对误差（MAD）与平均相对误差（MRD）量化模拟结果与实验结果的偏差，MAD与MRD的定义如下

式中，U代表传热系数与摩擦压降梯度。

图4为模拟传热系数与Cavallini等［16］和Shah［17］的经验公式对比情况。二者公式均对冷凝流动利用Froude数进行分区，对不同的区域采用不同的计算模型，而方法基本一致，即在管内单相湍流强制对流的换热关联式（Dittus-Boelter公式）的基础上添加两相修正因子。由图4可得，经验公式可以较好预测模拟结果，圆形与方形通道模拟结果基本在预测值的±30%以内。由表2可得，Shah［17］公式可以较好预测模拟结果，圆形与方形通道的MAD分别为8.54%和10.32%。

图4　传热系数模拟结果与公式的对比Fig.4　Comparison of numerical heat transfer coefficients with empirical correlations

表2　R换热与压降经验公式的MAD和MRDTable 2　MAD and MRD for heat transfer and pressure drop correlations

图5为摩擦压降梯度的模拟值与Zhang等［18］、Kim等［19］、Li等［20］、Zhang等［21］的经验公式的对比情况。4组公式均采用两相分离模型，其中Zhang等［18］公式为实验值拟合得到，而其他3组均为提取大量文献实验结果，构建足够丰富的压降数据库，分析修正Chisholm因子获得。由图5可得4组压降公式可以较好预测模拟结果，其中圆形与方形通道模拟结果基本在预测值的±40%与±20%以内。由表2可得，Li等［20］公式（MAD=14.88%，MRD=-8.76%）可以较好预测圆形通道模拟结果，而Zhang等［21］公式（MAD=10.90%，MRD=3.85%）可以较好预测方形通道模拟结果。综合传热系数与压降梯度与经验公式的对比，可以得到模拟传热传质模型的选择是可靠的。

2.4汽液界面轮廓图

本文模拟中假设壁面温度与汽液界面温度恒定，传热系数主要由液膜厚度以及液膜区域的湍流黏度确定。图6为圆形与方形通道内，G为317、715 kg·m-2·s-1时，汽液界面的分布情况，其中对方形通道进行了比例缩放。由图6可得，对于圆形通道，在高干度情况下液膜厚度基本均匀。随着干度的降低，液膜在重力的作用下逐渐向通道底部集聚，而通道顶部的液膜厚度基本不变。随着质量流量的增大，顶部的液膜厚度增大，而底部的液膜厚度降低。对于方形通道，液膜主要集聚在通道的角落位置，而四周管壁中间附近的液膜厚度较薄。随着质量流量的增大，在相同干度下，角落附近的液膜厚度逐渐降低，同时薄液膜所占通道周长的比例逐渐增大，平均换热效果提升。

图5　压降梯度模拟结果与公式的对比Fig.5　Comparison of numerical pressure drop gradients with empirical correlations

2.5液膜厚度

图7为圆形与方形通道内，G为531 kg·m-2·s-1时，液膜厚度沿圆心角的分布情况。由图7（a）可得，液膜厚度在圆管上部基本稳定，约为25 μm。由于重力的作用，液膜逐渐积聚在圆管下部，厚度随着θ的增大逐渐提高。随着干度的降低，蒸汽冷凝量增加，重力对液膜的积聚作用增强，底部的液膜厚度逐渐增加。同时，液膜厚度骤增的位置对应的θ随着干度的增大而逐渐增高，表明在高干度时，薄液膜区域所占比例更高。

图6　圆形与方形通道内汽液界面形状Fig.6　Vapor-liquid interfaces in circular and square channels

由图7（b）可得，方形通道内液膜主要积聚在角落位置（θ为45°、135°），而管壁中间位置区域（θ为0°、90°、180°）液膜较薄。相对圆形通道，方形通道内表面张力的作用更强，而重力的作用相对较小。随着干度的降低，角落位置的液膜厚度逐渐增大，而管壁中间区域的液膜厚度以及薄液膜所占的区域逐渐降低，导致传热系数随着干度的降低而降低。

对于冷凝流动，传热系数与液膜厚度呈反比。对于圆管，通道上侧区域传热系数较大，蒸汽更容易在此处凝结为液体，而对于方形通道，整个换热部分主要集中在四周管壁的中间位置。由图7可得，方形通道内液膜厚度小于圆形通道，换热效果优于圆形通道。

图7　圆形与方形通道内液膜厚度Fig.7　Liquid film thicknesses in circular and square channels

3　结　论

通过数值模拟研究了水平微细圆形与方形通道内的冷凝流动换热阻力特性，得到如下结论。

（1）传热系数随着质量流量、干度的增大而增大，方形通道的传热系数高于圆形通道。

（2）摩擦压降梯度随着质量流量增大而提高，当x＜0.85时，随着干度的增大而增高。同样，方形通道的压降要高于圆形通道。

（3）模拟所获得的传热系数与摩擦压降梯度可以较好地吻合文献经验公式。

（4）圆形通道内的液膜集聚于通道底部，而方形通道的液膜主要集中于通道角落区域。相对圆形通道，方形通道内表面张力的作用更强，而重力的作用相对较小。

（5）薄液膜区域所占的比例随着干度的增大而增大，方形通道内的液膜厚度要小于圆形通道，换热性能优于圆形通道。

符号说明

cp——比定压热容，J·kg-1·K-1

dh——当量直径，mm

E——比热力学能，J·kg-1

F——动量方程源项，N·m-3

G——质量流量，kg·m-2·s-1

g——重力加速度，m·s-2

h——传热系数，W·m-2·K-1

hlv——汽化潜热，J·kg-1

k——热导率，W·m-1·K-1

m——相变质量源项，kg·m-3·s-1

MAD——平均绝对误差

MRD——平均相对误差

r——质量源项系数，s-1

T——温度，K

v——速度矢量，m·s-1

x——干度

α——单元格体积分数

δ——液膜厚度，μm

θ——角度，（°）

μ——动力黏度，kg·m-1·s-1

ρ——密度，kg·m-3

σ——表面张力，N·m-1

下角标

a——加速压降

cal——计算值

f——摩擦压降

l——液相

sat——饱和状态

sim——模拟值

tp——两相

v——汽相

References

［1］杨英英，李敏霞，马一太. 水平光滑细管内R32冷凝换热的流型特性［J］. 化工学报， 2014， 65（2）： 445-452. DOI： 10.3969/j.issn. 0438-1157.2014.02.011. YANG Y Y， LI M X， MA Y T. Characteristics of flow pattern for condensation heat transfer of R32 in horizontal small tube ［J］. CIESC Journal， 2014， 65（2）： 445-452. DOI： 10.3969/j.issn.0438-1157. 2014.02.011.

［2］ ILLÁN-GÓMEZ F， LÓPEZ-BELCHÍ A， GARCÍA- CASCALES J R，et al. Experimental two-phase heat transfer coefficient and frictional pressure drop inside mini-channels during condensation with R1234yf and R134a ［J］. Int. J. Refrig.， 2015， 51： 12-23.

［3］ SAKAMATAPAN K， KAEW-ON J， DALKILIC A S， et al. Condensation heat transfer characteristics of R-134a flowing inside the multiport minichannels ［J］. Int. J. Heat Mass Transfer， 2013，64（0）： 976-985

［4］ LIU N， LI J M， SUN J， et al. Heat transfer and pressure drop duringcondensation of R152a in circular and square microchannels ［J］. Exp. Therm. Fluid. Sci.， 2013， 47： 60-67.

［5］ WANG H S， ROSE J W. A theory of film condensation in horizontal noncircular section microchannels ［J］. J. Heat Transfer， 2005，127（10）： 1096-1105.

［6］ WANG H S， ROSE J W. Film condensation in horizontal microchannels： effect of channel shape ［J］. Int. J. Therm. Sci.， 2006，45（12）： 1205-1212.

［7］ WANG H S， ROSE J W. Theory of heat transfer during condensation in microchannels ［J］. Int. J. Heat Mass Transfer， 2011， 54（11/12）：2525-2534.

［8］ DA RIVA E， DEL COL D. Numerical simulation of laminar liquid film condensation in a horizontal circular minichannel ［J］. J. Heat Transfer， 2012， 134（5）： 051019-051019.

［9］ DA RIVA E， DEL COL D， GARIMELLA S V， et al. The importance of turbulence during condensation in a horizontal circular minichannel ［J］. Int. J. Heat Mass Transfer， 2012， 55（13/14）：3470-3481.

［10］刘纳，李俊明. R32 在水平微细圆管内凝结换热的数值模拟［J］.化工学报， 2014， 65（11）： 4246-4253. DOI： 10.1080/10407782. 2015.1081029. LIU N， LI J M. Numerical simulation of R32 condensation heat transfer in horizontal circular microchannel ［J］. CIESC Journal， 2014，65（11）： 4246-4253. DOI： 10.1080/10407782.2015.1081029.

［11］ EL MGHARI H， ASBIK M， LOUAHLIA-GUALOUS H， et al. Condensation heat transfer enhancement in a horizontal non-circular microchannel ［J］. Appl. Therm. Eng.， 2014， 64（1/2）： 358-370.

［12］ LEE W H. A pressure iteration scheme for two-phase flow modeling［J］. Multiphase Transport Fundamentals， Reactor Safety， Applications，1980， 1： 407-431.

［13］ WEI J， PAN L， CHEN D， et al. Numerical simulation of bubble behaviors in subcooled flow boiling under swing motion ［J］. Nucl. Eng. Des.， 2011， 241（8）： 2898-2908.

［14］ YANG Z， PENG X， YE P. Numerical and experimental investigation of two phase flow during boiling in a coiled tube ［J］. Int. J. Heat Mass Transfer， 2008， 51（5）： 1003-1016.

［15］ DEL COL D， BORTOLATO M， AZZOLIN M， et al. Condensation heat transfer and two-phase frictional pressure drop in a single minichannel with R1234ze（E） and other refrigerants ［J］. Int. J. Refrig.，2015， 50： 87-103.

［16］ CAVALLINI A， DEL COL D， DORETTI L， et al. Condensation in horizontal smooth tubes： a new heat transfer model for heat exchanger design ［J］. Heat Transf. Eng.， 2006， 27（8）： 31-38.

［17］ SHAH M M. An improved and extended general correlation for heat transfer during condensation in plain tubes ［J］. HVAC&R Res.， 2009，15（5）： 889-913.

［18］ ZHANG M， WEBB R L. Correlation of two-phase friction for refrigerants in small-diameter tubes ［J］. Exp. Therm. Fluid. Sci.， 2001，25（3）： 131-139.

［19］ KIM S， MUDAWAR I. Universal approach to predicting two-phase frictional pressure drop for adiabatic and condensing mini/micro-channel flows ［J］. Int. J. Heat Mass Transfer， 2012，55（11/12）： 3246-3261.

［20］ LI W， WU Z. A general correlation for adiabatic two-phase pressure drop in micro/mini-channels ［J］. Int. J. Heat Mass Transfer， 2010，53（13/14）： 2732-2739.

［21］ ZHANG W， HIBIKI T， MISHIMA K. Correlations of two-phase frictional pressure drop and void fraction in mini-channel ［J］. Int. J. Heat Mass Transfer， 2010， 53（1/2/3）： 453-465.

Numerical simulation of condensation in horizontal circular and square minichannels using R134a

ZHANG Jingzhi1，2， LI Wei1
（1College of Energy Engineering， Zhejiang University， Hangzhou 310027， Zhejiang， China；2Collaborative Innovation Center of Advanced Aero-Engine， Hangzhou 310027， Zhejiang， China）

Heat transfer and pressure drop characteristics of condensation for R134a at saturation temperature of 320 K inside horizontal circular and square minichannels were investigated numerically. The results indicated that the heat transfer coefficients and frictional pressure drop gradients increased with mass flux and vapor quality，while the pressure drops decreased with increasing vapor quality at x＞0.85. Compared with the circular tube， the square channel with the same perimeter as the corresponding circular tubes can enhance heat transfer coefficients and increase the pressure losses. The numerical results agreed well with the well-known empirical correlations for condensation. A thicker liquid film was obtained at the bottom of the round tube， while the liquid film for the square channel accumulated at the bottom and the middle top of the channels at lower vapor quality. The proportion of the thinner liquid film region， which corresponded to a higher heat transfer coefficient， increased with increasing vapor quality， leading to a higher heat transfer coefficient at higher vapor quality. The liquid film thicknesses in square channels were lower than that in circular channels， thus enhancing the heat transfer.

condensation； minichannels； numerical simulation； heat transfer； pressure drop