基于ANSYS的载货汽车车架静动态性能分析*

黄玉亭 李韶华 ，2 杨绍普 ，2

（1.石家庄铁道大学；2.河北省交通安全与控制重点实验室）

车架是发动机、车体、传动部件及外部载荷的基础和关键承载部件，它承受的载荷包括汽车车身质量和行驶时受到的冲击、扭曲及惯性力等。由于车架受力的复杂性，合理的设计目标不容易实现，但车架强度、刚度性能的好坏直接影响汽车行驶过程的安全性及可靠稳定性[1-2]。因此，有必要对汽车车架的刚度及强度进行验证分析[3-5]，同时对车架有限元模型进行动力特性分析，得到车架固有频率及振型，为汽车车架动态设计提供理论参考[6-7]。通过阅读文献，车架在瞬态响应分析方面研究较少，但瞬态冲击不仅影响车架的使用寿命，还影响汽车行驶平顺性[8-11]。文章还以汽车通过减速带时的工况为例，分析车架在冲击载荷作用下动力响应，得到车架的位移响应曲线。

1 车架建模

文章以某重型三轴载货汽车为例，其车架为边梁式，由位于两边的2根纵梁和11根横梁组成。车架长11 398 mm，宽860 mm，高302 mm，前轴与后前轴的轴距为5 700 mm，2个后轴轴距为1 300 mm。一般情况下，车架纵梁的横截面做成等截面，但也有变截面的情况，这依赖于汽车的不同用途和整车的布置情况，文章所研究的重型汽车前面承受的载荷相对较小，纵梁前横截面可以较小一些，后端承受载荷较大，故纵梁后截面较宽一些，前截面翼面宽度尺寸为70 mm，后截面为90 mm，车架总成三维模型，如图1所示。

图1 某重型三轴载货汽车车架三维模型图

定义车架的材料属性，如表1所示。为了对模型进行更加精确的分析，忽略一些次要的零件，在不影响精度的前提下对该模型进行简化，将简化后的模型导入有限元软件ANSYS中，再对该模型进行网格化。网格化决定单元的数量及网格尺寸，网格划分较大，形成的单元数量较少，计算精度不高，反之，网格较小，单元数量较多，计算精度得到提高，但是极大地降低了计算机的工作效率。因此，要根据模型复杂程度及结构特点合理的划分网格。考虑到该模型结构复杂，需要进行简化处理后，采用自由划分网格的方式划分，节点数共44 860个，网格单元数20 646个，最终建立的车架局部有限元模型，如图2所示。

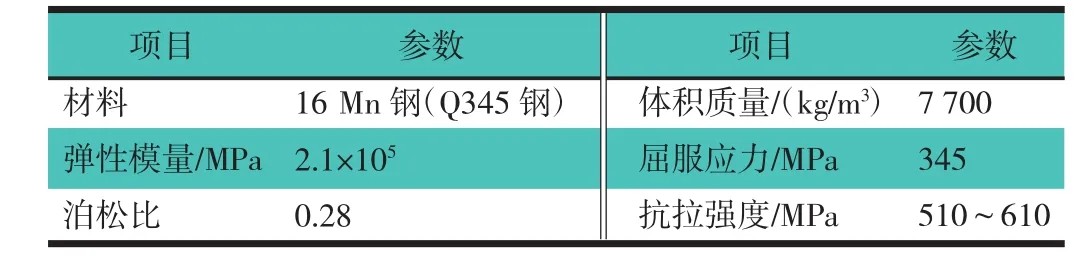
表1 某重型三轴载货汽车车架材料特性

图2 某重型三轴载货汽车车架局部有限元模型图

2 车架静力分析

汽车在行驶过程中，典型的静力分析工况主要包括弯曲、扭转、急刹制动及转弯4种工况。其中，弯曲和扭转是2种对车架影响较大的工况，因此文章对车架结构主要分析这2种工况。通过计算在固定不变载荷下车架结构位移、应力及应变，并对车架强度、刚度进行校核，保证了结构安全和正常工作，同时又满足设计轻量化和经济性的需求。

2.1 载荷处理

主要的弯曲载荷是由车架自身质量和外加质量产生的，包括悬挂在车架上的总成、车厢及货物质量。扭转载荷是由汽车在行驶过程中遇到路面不平引起的非对称性支撑载荷。

由于对车架的分析校核是为了验证刚柔耦合模型中弹性车架可靠度，所以在静力学分析中，货物的质量（19 000 kg）按均布载荷分布在2根纵梁上，发动机（900 kg）、变速箱（260 kg）、驾驶舱（1 000 kg）、驱动轴（175 kg/个）及其它附件的质量（540 kg）按其安装位置施加集中载荷，为保证车架静力分析时有限元模型不产生刚性位移，施加载荷前要对模型进行约束处理，对车架与悬架接触位置根据不同需要进行限制，保证车架不同工况下有足够的自由度约束。

2.2 弯曲工况

弯曲工况是指汽车满载状态下，在良好路面匀速直线行驶时四轮着地的情况。在有限元分析过程中，车架承受的质量和载荷要乘以一定的动载荷系数，而动载荷系数受外界条件的约束，所以根据半经验值取动载荷系数为2.5适宜。约束施加在前后悬架弹簧支撑车架的相应节点上，总共施加约束6处，限制每个节点6个方向的自由度，运行分析结果，如图3和图4所示。

图3 车架弯曲工况应力分布图

图4 车架弯曲工况位移分布图

2.3 扭转工况

扭转工况同样是在满载状态下，汽车在不同路面行驶而导致一个前车轮悬空时车架的受力。左前悬架与车架接触处，不施加任何约束，其余接触点限制所有自由度。而扭转工况多数发生在较差路面，行驶车速较低，所以惯性载荷较小，此时最大动载荷系数取1.25较宜。运行分析结果，如图5和图6所示。

图5 车架扭转工况应力分布图

图6 车架扭转工况位移变形图

由图3和图5可以看出，由于车架后部自由端相对较长，受到载荷时易发生变形，此处为车架在该状态下受到的最大应力，约200 MPa，最小应变在车架前端第1根横梁处。根据该车架使用的低合金钢材料可知其屈服应力为345 MPa，则车架的结构安全系数为：

式中：σmax——车架材料的屈服极限，MPa；

σx——不同工况下计算出的车架最大应力值，MPa。

当σ＞1时，说明车架在该工况下结构刚度满足要求，否则，车架刚度不符合要求。文章中，σ=345 MPa/200 MPa=1.725，说明该车架结构强度满足要求。从图6可以看到，车架绕z轴上下弯曲，纵梁的尾部及第7，8根横梁处位移变化最大，为11.56 mm，这是由于车架受到载荷作用时后部车架受到的约束较少，因此易发生变形。

3 车架模态分析

模态分析一般用于分析结构的振动特性，是动力学分析的起点和基础。根据模态理论可知，车架结构的振动可以表现为各阶固有弯曲和扭转阵型的线性组合。一般情况下，汽车车架低阶振型对汽车行驶平顺性影响较大，为此只分析车架的低阶固有频率及相应的振型。车架自由状态下在前后轴6个受力支撑点固定约束，划分网格，运行分析后可得到车架的5阶固有频率值及振型，如图7所示。

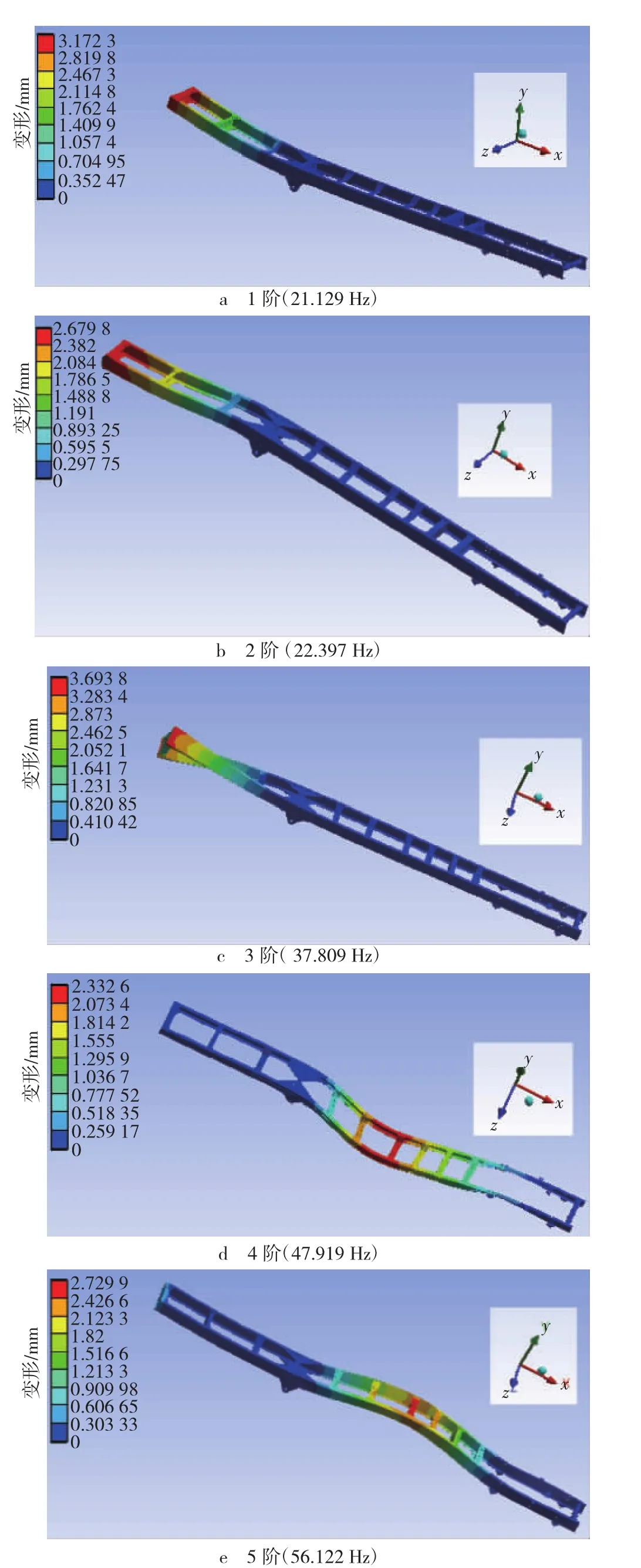
图7 车架固有频率和振型图

由图7可知，车架的1阶频率为21.129 Hz，主要变形是车架绕z轴上下弯曲；2阶频率为22.397 Hz，主要为车架绕y轴左右弯曲，发生在车架纵梁中后部；3阶频率为37.809 Hz，主要为绕x轴的扭转，发生在车架的后部和10，11根横梁上；4阶频率为47.919 Hz，绕y轴在z轴方向弯曲和绕x轴扭转；5阶频率为56.122 Hz，主要绕z弯曲在y方向上弯曲和绕x轴扭转，主要发生在车架中部。而车架之所以会有上述弯曲和扭转情况，就是因外界激励产生的振动频率达到车架结构的固有频率，随之引起车架发生共振，影响车架和汽车的寿命。为了避免这种情况的发生，要尽力避开外界这种激励作用产生的各阶频率范围。

4 车架瞬态动力学分析

瞬态动力学分析是时域分析，分析结构在随时间变化的载荷作用下动力响应的过程。其输入数据作为时间函数的载荷，而输出结果是随时间变化的位移等量。文献[12]利用ADAMS软件对重型汽车以不同车速通过不同类型减速带，得到重型汽车转向轮垂向轮胎力值的大小。文章仅分析汽车转向轮通过高度为12 mm，宽度为600 mm的减速带时车架受到的瞬时冲击力。汽车悬架隔振系数选为45%[13]，则车架受到的瞬态冲击力是转向轮轮胎力幅值的45%。假定汽车以60 km/h通过减速带，受到障碍对车轮的反作用冲击力为6.5×104N，该结构的阻尼大小为0.05。在模态分析的基础上，设置动态力载荷（载荷作用在前悬架与车架的接触位置）和时间步骤进行瞬态动力学分析，得到车架转向轮处的瞬态冲击力作用下变形分析云图和位移响应曲线，如图8和图9所示。

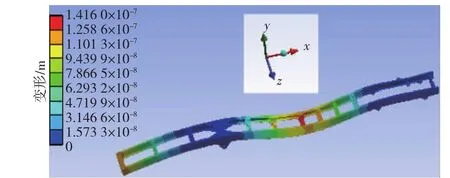
图8 车架瞬态分析变形云图

图9 车架瞬态分析位移响应曲线

从图8可以看到，汽车转向轮在过减速带时，受到瞬态冲击，该作用力使车架发生绕z轴弯曲和绕x轴扭转变形，最大变形发生在第5根横梁处，除车架中部发生较大变形外，车架尾部也会受到些许的弯曲变形。而作用点处位移随时间变化曲线，如图9所示。由于存在结构阻尼引起能量消耗，随着时间载荷的增加，应变增大，在0.11 s达到最大，为0.101 mm。随后载荷逐渐衰减，位移响应曲线呈现下降趋势，直至0.5 s时应变趋于0，车架慢慢趋于平稳。

5 结论

通过仿真分析可以看出，车架在弯曲和扭转工况下的最大应力接近200 MPa，远小于车架结构的屈服极限，刚度和强度均满足结构要求，且车架扭转刚度对车架的刚度影响偏大。模态分析得到柔性车架低阶固有频率，为汽车设计提供理论参考。瞬态冲击影响车架的使用寿命和行驶平顺性，该分析验证了车架能够满足结构设计的同时，也为车架导入整车模型，建立刚柔耦合汽车平顺性分析提供前提。