呈现不同统计图,感受别样精彩
2016-08-19余旭红
余旭红
呈现不同统计图,感受别样精彩
余旭红

苏科版数学八年级下册教材第15至16页例题呈现了2000年我国每10万人中具有各类文化程度人数的条形统计图和扇形统计图.今天我们就从这道题入手,探究例题的解题结论如何在问题变式中得到有效应用,帮助同学们更好地感受条形统计图、扇形统计图和折线统计图在实际生活中的应用.
一、课本例题的解题结论
课本呈现了2000年我国每10万人中具有各类文化程度人数的条形统计图和扇形统计图,如图1与图2.

图1 2000年我国每10万人中具有各类文化程度人数的条形统计图

图2 2000年我国每10万人中具有各类文化程度人数分布的扇形统计图
结论:条形统计图、扇形统计图和折线统计图是三个重要的统计图,它们都可以非常直观地表示数据.其中条形统计图是用宽度相同的“条形”的高度表示数据;扇形统计图主要用于表示总体中各组成部分所占的百分比;折线统计图是用折线表示数据的变化特征,用于反映事物的变化过程和趋势.例题的呈现说明在同一信息与数据下,条形统计图和扇形统计图是可以相互转化的,同样,折线统计图也可以和条形统计图或扇形统计图转化.
二、例题的变式训练
(一)呈现一种统计图,尝试画另一种统计图
变式一光明中学对某班45名学生初中三年中戴近视眼镜人数进行了跟踪调查,统计数据如图3-1所示.

图3-1 某班学生初中三年中戴近视眼镜的人数统计图
(1)如果用整个圆代表该班人数,请在图3-2中画出该班七年级初戴近视眼镜人数和未戴近视眼镜人数扇形统计图,并标出百分比;

图3-2

图3-3
(2)如果用整个圆代表该班人数,请在图3-3圆中画出该班九年级末戴近视眼镜人数和未戴近视眼镜人数扇形统计图,并标出百分比.
【解析】(1)根据条形统计图,可知该班七年级初戴近视眼镜人数为9,所占百分比
对应扇形的圆心角为360°×20%=72°;因此未戴近视眼镜人数所占百分比为1-20%=80%,对应扇形圆心角为360°×80%=288°.制作的扇形统计图如图4-1所示.
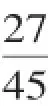

图4-1 七年级初戴和未戴近视眼镜人数分布统计图

图4-2 九年级末戴和未戴近视眼镜人数分布统计图
感悟:变式一呈现了统计图之间的转化.制作扇形统计图所需的数据由条形统计图获得,通过计算求出各部分占总体的百分比及其相应的扇形圆心角,体现了两种统计图之间的自然联系.
(二)呈现两种不完整统计图,尝试补全统计图
变式二博鳌亚洲论坛2014年年会于2014年4月8日在海南博鳌开幕,光明中学就同学们对博鳌亚洲论坛的了解程度,随机抽取了部分学生进行问卷调查,并根据收集的信息进行了统计,绘制了下面两幅尚不完整的统计图.根据图5所提供的信息解答下列问题:

图5 光明中学学生对博鳌亚洲论坛的了解程度折线统计图和扇形统计图
(1)该校参加问卷调查的学生有_______名;
(2)补全两个统计图.
【解析】(1)由折线统计图可知“了解很少”的有25人,由扇形统计图可知其所占百分比为50%,由此可求出参加问卷调查的学生总人数为25÷50%=50;
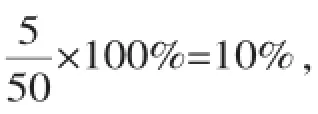
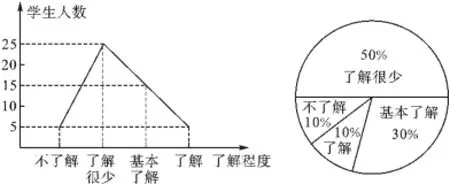
图6 光明中学某校学生对博鳌亚洲论坛的了解程度折线统计图和扇形统计图
感悟:变式二考查了如何从两幅不完整的统计图中正确读取信息的能力.通过两种统计图之间数据信息的分别读取,巩固了折线统计图和扇形统计图的画法,感受了不同统计图的优点和在实际生活中的应用.
(三)呈现两幅完整统计图,尝试解决实际问题
变式三在变式二的基础上,提出以下两个问题:
(1)若光明中学有1 500名学生,那么该校有多少名学生达到基本了解以上(含基本了解)的程度?
(2)为了让更多学生更好地了解博鳌亚洲会,学校举办了两期专刊.之后又进行了一次调查,结果全校已有1176名学生达到了基本了解以上(含基本了解)的程度,如果每期专刊发表之后学生达到基本了解以上(含基本了解)程度的增长百分数相同,试求这个百分数.
【解析】(1)∵样本中,达到基本了解以上(含基本了解)的程度的学生占样本总数的40%,
∴1 500×40%=600.
∴该校有600名学生达到基本了解以上(含基本了解)的程度.
(2)设这个百分数为x,根据题意可得600(1+x)2=1 176,
可得(1+x)2=1.96,解得x1=0.4,x2=-2.4(负值不合题意舍去),
则这个百分数为40%.
感悟:变式三一方面体现了利用样本估计总体的思想,同时通过一元二次方程的求解,建立了不同数学内容之间的联系.
总之,三种统计图是中考的必考内容,同学们不仅要会根据具体数据画三种统计图,而且要不断增强从统计图中获取信息的能力,结合相关数学知识解决实际生活中的问题,感受做一题、通一类的别样精彩!
(作者单位:浙江省绍兴市柯桥区钱清镇中学)
