“通过计算探索规律”实验方案

孙晓祥



“通过计算探索规律”实验方案

孙晓祥

1.方案提出：“通过计算探索规律”的实验活动是师生一起对数的乘方（即幂的相关运算）的规律进行探索，同学们在经历“计算结果、观察猜想、验证结论、学以致用”整个过程的基础上，学会“发现问题、提出问题”，并通过“探究、合作”等手段，寻求解决问题的方法，并用来解决新的问题.“规律探索”型问题在历年中考也屡见不鲜，其中所蕴含解决问题的思想方法、策略、经验的积累正是新课程标准要求学生学习数学的价值体现.

2.实验目的：（1）进一步理解整数指数幂的意义及其基本运算法则，借助于计算器，引导同学们通过计算、观察、猜想揭示规律，提高归纳能力；

（2）经历不同问题的操作、观察、比较、猜想、归纳、交流，感受和积累“从具体到抽象、从特殊到一般”的思想方法；

（3）发展同学们的符号意识.

3.实验重点：通过实验培养归纳、合情推理的能力，感悟“从具体到抽象、从特殊到一般”的数学思想方法.

4.实验时间：45分钟.

5.实验准备：计算器.

6.实验过程：

一、交流展示、探究引入

1.播放视频，简单介绍著名数学猜想——“哥德巴赫猜想”

【活动说明】引导同学们感受有些“伟大的科学发现”是经过“计算、观察、猜想”得到的，激发学习、探究的兴趣与欲望.

2.（1）下列各式是个位数是5的整数的平方运算.各等式右边数的末两位上的数有什么特点？观察各式中其余数位上的数字，你有什么发现？

（2）根据你发现的规律，猜想下列各式的结果：

452=_______，552=_______，

652=_______，752=_______，

952=_______，1152=_______，

1952=_______.

（3）利用计算器验算（2）中各式的结果是否正确.

二、自主质疑、互动解惑

活动1计算——感悟

1.（1）观察下列各式：

3×5，33×35，333×335，3 333×3 335.

（2）计算并写出（1）中各式的结果.

（3）你能发现（1）中各式的结果有什么规律吗？

（4）根据你发现的规律尝试填写下列空格：

3 333 333×3 333 335=_____________；

（）×（）=1111111155555555.

（5）利用计算器验算（4）中的式子是否正确.

2.（2014·云南省）观察规律并填空.

……

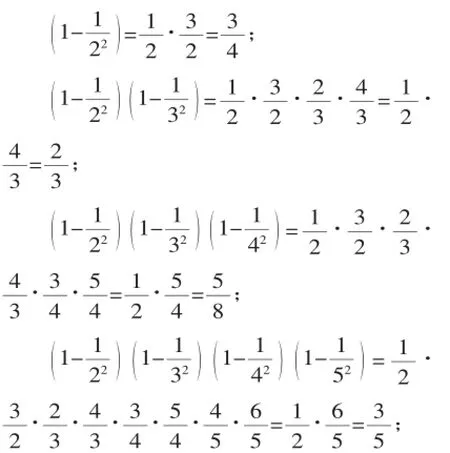
3.（2014·甘肃兰州）为了求1+2+22+ 23+…+2100的值，可令S=1+2+22+23+…+2100，则2S=2+22+23+24+…+2101，因此2S-S=2101-1，所以S=2101-1，

即1+2+22+23+…+2100=2101-1.

仿照以上推理计算1+3+32+33+…+32014的值是_______.

【活动说明】通过对三道习题的探究，进一步感悟数（幂）的计算在“规律探索”中的应用与方法，体会问题不同但解决策略、基本思路相同，即都应用了“计算结果、观察猜想、验证结论、学以致用”的探索路径，使学生进一步积累数学活动经验.

活动2互评——交流

1.小组内同学之间互相交流：①分别说说上述三个问题的特征、发现的规律；②交流如何应用发现的规律解决新问题.

2.推荐小组代表全班讲题交流：①上述三个问题的规律是什么？如何发现的？②“问题解决”如何思考？③这三个活动的规律探索有什么共同特征？你积累了什么经验？④你还能提出什么问题？

【活动说明】安排此环节主要基于以下思考：从发现到表达交流是能力提升的过程，在倾听、思辨、争鸣中统一基本认识还能追求“求同存异”，为提出新的问题提供生长点.

活动3解题——应用

1.（1）计算：9×6=_______，99×96= _______，999×996=_______，

9 999×9 996=_______，99 999×99 996= _______；

（2）与同伴交流，探讨计算中的规律；

（3）运用已发现的规律，直接写出下式的计算结果：

999 999 999×999 999 996=_________.

2.先请你计算下列各式：

21×29=_______，34×36=_______，42× 48=_______，53×57=_______，

64×66=_______，75×75=_______，……

（1）你有什么新的发现？

（2）再多写些有上述式子特征的算式，验证你的发现.

3.4100的个位数字是几？还有其他想法吗？932016的个位数字呢？

三、分层训练、巩固提高

1.（2014·安徽省）观察下列关于自然数的等式：

32-4×12=5①

52-4×22=9②

72-4×32=13③

……

根据上述规律解决下列问题：

（1）完成第四个等式：92-4×_______2= _______；

（2）写出你猜想的第n个等式（用含n的式子表示），并验证其正确性.

2.阅读下面的材料，并完成填空.

你能比较两个数20152016与20162015的大小吗？为了解决这个问题，现将问题一般化，即比较nn+1和（n+1）n的大小（n≥1的整数），然后从分析n=1、2、3、4、5……这些简单情况入手，从中发现规律，经过归纳猜想得出结论.

（1）通过计算比较下列各组两个数的大小（在横线上填“＞”“＜”或“=”）

①12_______21；②23_______32；

③34_______43；④45_______54；

⑤56_______65.

（2）根据第（1）小题结果经过归纳，可以猜想nn+1和（n+1）n有怎样的大小关系？

（3）根据上面的归纳猜想得到的一般结论，判断20152016与20162015的大小关系.

【活动说明】活动主要目的是引导大家在积累基本活动经验的基础上进行巩固练习、进行变式训练，引导大家回归到已有的数学知识、生活经验，挖掘提炼解决问题的策略、思想方法，进一步提炼解决问题的方法策略以及提高归纳、猜想的能力.

四、归纳反馈、拓展延伸

1.（2014·甘肃白银、临夏）观察下列各式：

……

猜想13+23+33+…+103=_______.

2.在本节课的探究过程中，你有哪些感受与收获？回顾你的探究心路历程，请将你的探究经验、感悟和发现写成学习体会或数学小论文.

【活动说明】撰写学习体会或数学小论文就是以“数学写作活动”来指导学习或学习反思，它是学生将所学知识、技能、经验、思想方法进一步“内化”的一种过程，对理解数学、表达数学和应用数学起着很重要的作用.

附：活动的评价

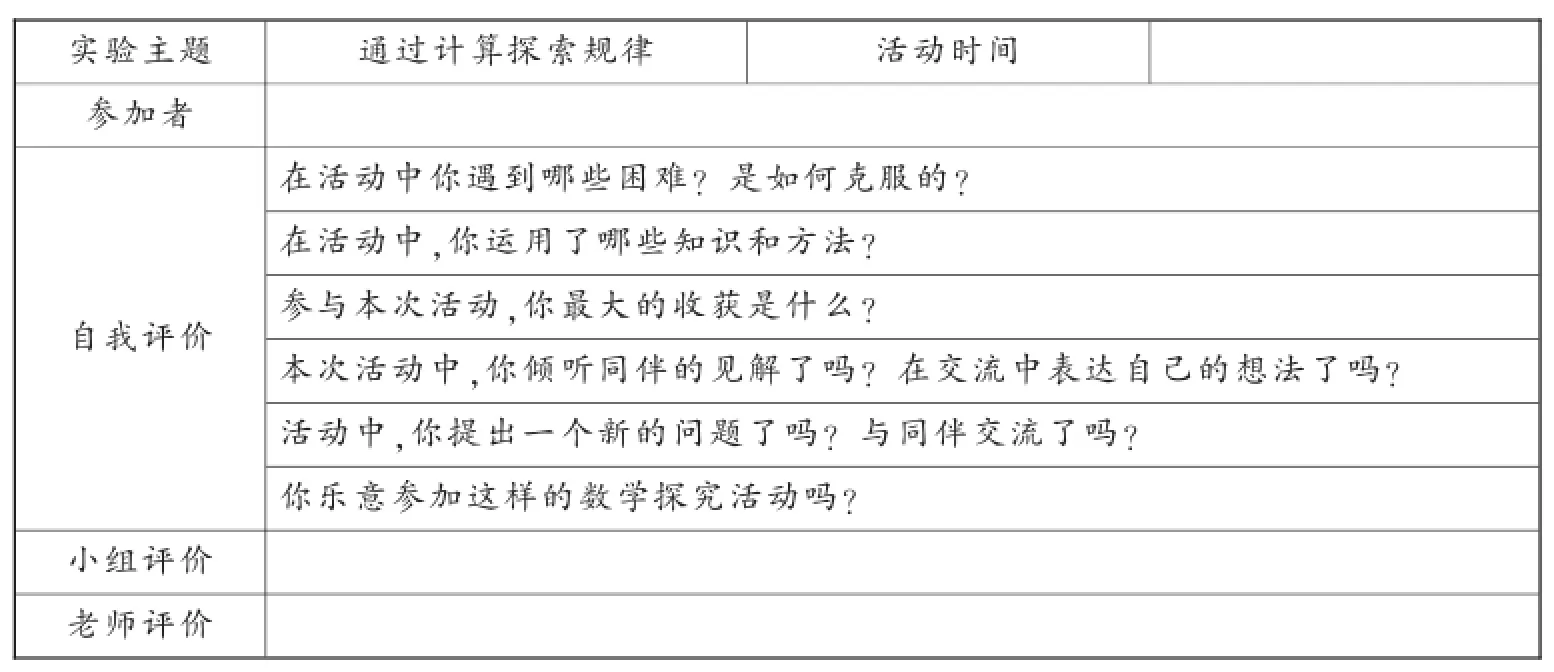
数学实验活动评价表

【活动说明】数学探究性学习的评价应突出过程性评价，重点评价自己在探究过程中对问题的理解、思辨与情感态度的投入程度，也要学会倾听同学、老师的意见，提高学习的效率.

（作者单位：江苏省泰州中学附属初级中学）