深入本质 一通百通

江美红



深入本质 一通百通

江美红

整式的乘法是一种重要的代数恒等变换，它是今后学习分式运算、解一元二次方程等内容的基础，是中考必不可少的一部分内容.面对这部分内容，许多同学的反应往往是：“老师讲的听不懂，烦，愁.”“每次我都很认真地听，可总似懂非懂，考试总考不好，我头痛.”要改变现状，我们需要打好基础，寻找规律，举一反三、一通百通.

一、问题解答

例1计算：（x+2y-1）（x-2y+1）.

【解析1】

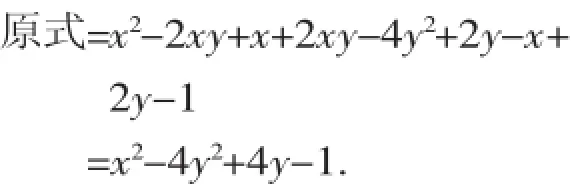
【点评】利用多项式乘多项式的法则解题，三项式乘三项式，展开得九项式，再合并同类项.

【解析2】

【点评】利用整体思想，转化为二项式乘二项式，展开得四项式，再利用平方差公式展开，最后合并同类项.

【解析3】

【点评】利用整体思想构造平方差公式，再利用完全平方公式展开.

二、寻找规律

此题还有更多的解法.那么为什么有这么多的解法呢？这些解法是怎么想出来的？这其中有什么秘密吗？

这其中蕴含了很多的规律.

1.知识规律

这中间包含了多项式与多项式的乘法、平方差公式和完全平方公式，它们之间的联系如图所示.正是因为有了这些关系，才会使题目有多种解法.

2.解题规律

（1）选用多项式与多项式的乘法计算与选用平方差公式和完全平方公式计算都能解决问题，这是因为这三个公式是“一伙”的.

（2）题中若有“形”，则选定一种公式直接解题.比如出现（a+b）（a-b）形，则选用平方差公式；若出现（a+b）2与（a-b）2形，则选用完全平方公式.

（3）题中若无“形”，选定一种方法，造出它的“形”，比如解析3运用平方差公式，那就要把2y-1看作整体，造出平方差公式的“形”，即［x+（2y-1）］［x-（2y-1）］，再用平方差公式解题.而在解析2中要用平方差公式，就把x+2y与x-2y看作整体，造出（x+2y）·（x-2y），再利用平方差公式解题.

值得一提的是，虽然各种方法都能到达成功的彼岸，但还是要在平时的练习中积累经验，选择最佳方法解题.

三、一通百通

例2计算：（x+2y）（x-2y）（x2+4y2）.

【分析】题中有平方差公式的“形”，直接利用公式计算.

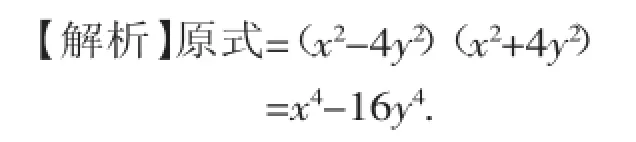
例3计算：（2x+3y）2（2x-3y）2.

【分析】题中虽无“形”，但有“隐形”，逆用积的乘方，造出平方差公式的“形”，再利用完全平方公式计算.

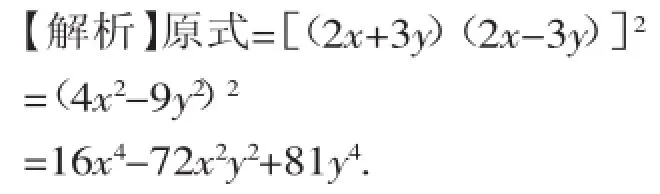
例4计算：（m-n-3）2.

【分析】题中虽无“形”，但也有“隐形”，可把m-n看作整体，造出完全平方公式的“形”.

例5计算：20152-2014×2016.

【分析】题中无“形”，也无“隐形”，利用数字之间的关系造出公式的“形”.

例6已知a2-b2=6，a-b=-3，求a+b的值.

【分析】题中有平方差公式的“形”，直接利用公式计算.

例7已知a-b=3，ab=2，求a2+b2的值.

【分析】题中虽无“形”，但也有“隐形”，即（a-b）2=a2-2ab+b2，直接利用公式计算.

在初中数学的每一章、每一节中都有知识规律与解题规律，掌握了规律，就能把难题变简单；解题找规律，就能一看就会、一通百通，你将会变得更有智慧，学习数学更轻松.

（作者单位：江苏省太仓市实验中学）