认清本质 灵活运用 突破难点
2016-08-19张晓东
张晓东
认清本质 灵活运用 突破难点
张晓东
整式乘法和因式分解是在整式这部分内容中最重要的两个知识,要正确地运用相关知识进行整式乘法和因式分解,除了要理解定义内涵之外,还要认清整式乘法和因式分解的本质.下面就和同学们就这部分中的符号问题、项数问题、正确区分两者之间关系及灵活运用四方面的难点进行剖析,希望对大家的学习有所帮助.
一、正确处理符号
例1计算:(-x-3y)(x-3y).
【分析】要正确计算本题的关键是要处理好符号,把它变形成为完全符合平方差公式的形式.观察发现第一个括号内两项都是负的,所以可以考虑提出负号,变形成为-(x+3y)(x-3y),这样对应到平方差公式中“a”就是x,“b”就是3y;从另外一个角度看,两个括号内3y项的符号相同、x项符号相反,所以可以考虑交换两项位置让其满足平方差公式.
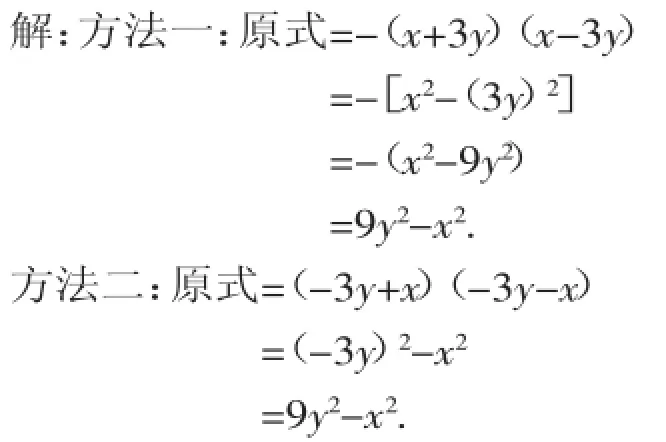
【点评】解答此类题目的关键是满足公式的形式,符号上必须满足和乘差才能运用平方差公式.当然,如果没有看出可以变形后运用公式,那就老老实实用整式乘法中多乘多的方法,一项一项相乘也是可以得到结果的.
例2计算:(-x-3y)2.
【分析】这个整式乘法明显符合完全平方公式,在计算中关键是符号的处理.我们可以把它看成为-x与3y差的平方,亦可以利用(-a)2=a2这一恒等式,把式子转化为(x+ 3y)2去计算.
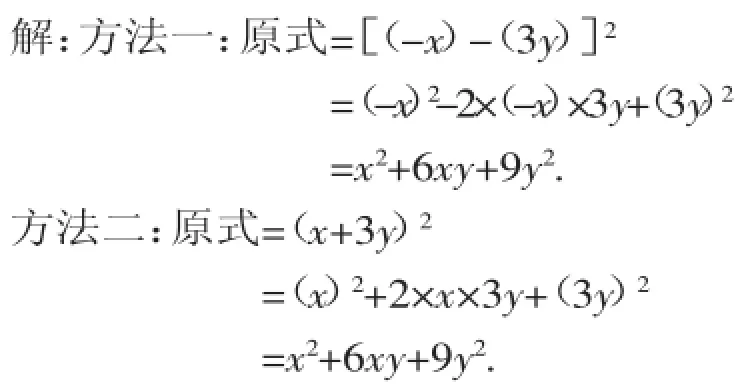
【点评】此类问题要求我们除注意公式的结构特点外,还要注意灵活处理式子中的符号.
例3因式分解:-x2+16y2.
【分析】多项式有两项,而且两项是平方形式,形式看起来不符合公式的特点,但两项符号是一正一负,所以只要调整两项位置或提取负号,就可以用平方差公式进行因式分解了.

【点评】平方差公式用来分解两项的多项式,但多项式必须满足两项可以写成平方形式,且两项符号要相反.只有通过相应的调整及提取符号,将形式变为和公式完全一致,分解起来才得心应手.
二、正确寻找“a”与“b”
例4计算:(x+3y-4)(x-3y+4).
【分析】本题是两个三项式相乘,和公式不太匹配(公式中只有两项),观察发现两个括号中第一项符号完全相同,可以看成公式中的“a”,二、三项符号相反,我们可以把后两项添括号后看成公式中的“b”,这样就符合了平方差结构特点.

【点评】两个公式中的“a”与“b”可以是单项式,也可以是多项式,在碰到三项乘三项时,我们要注意观察符号的特点(一同两反或一反两同),通过添括号把三项转化成两项,进而用公式进行计算.
例5计算:(x+y-1)2.
【分析】若将其中两项看成一项,即符合完全平方结构,即数学中的“整体思想”的体现.

【点评】此题还可以把后面两项添括号得[x+(y-1)]2,再把x和(y-1)看成为公式中的“a”与“b”,两种不同处理方法的本质是一样的,都是要把三项变为两项.有些同学错误地把这类计算直接算成为x2+y2-1,这是把本题和积的乘方性质混淆了.
三、灵活运用整式乘法和因式分解
例6计算:(x-y)2-(x+y)2.
【分析】本题可以用完全平方公式将前后两部分展开,再进行整式加减运算.也可以把整个式子看成为x-y与x+y平方差形式,运用平方差公式写成乘积形式后进行合并,再去括号.
解:方法一:


【点评】在动笔做题前,大家首先要看清题目要求是计算,也就是最后结果中是没有括号的.很多没有看清楚的同学往往以为是因式分解问题.当然,方法一是本题的常规的做法,方法二是灵活的做法.
例7计算:512-51.1×50.9.
【分析】观察发现,将51.1和50.9分别写成51+0.1、51-0.1,就能产生平方差公式的结构.

【点评】灵活运用整式乘法和因式分解是这部分的难点,本题的突破口在于要观察到51.1和50.9的平均数正好是前面的底数51.如果用死算的方法做这道题,不仅计算量大,而且容易出错.
四、处理好几个代数式的关系
例8已知a+b=10且ab=4,求a2+b2.
【分析】此题求解的是与a2+b2有关的结论,已知条件为a+b=10,很自然会想到完全平方公式(a+b)2=a2+2ab+b2.
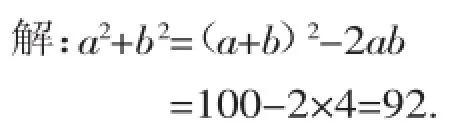
【点评】解决好此类问题的关键是要处理好“四兄弟”:a+b、a2+b2、ab及a-b之间的关系,常用的变形公式有:

(作者单位:江苏省太仓市沙溪实验中学)
