考虑加载过程及桩体固结变形的碎石桩复合地基固结解析解*

郭　彪　龚晓南　李亚军

(①云南省交通规划设计研究院陆地交通气象灾害防治技术国家工程实验室　昆明　650041)(②浙江大学　杭州　310058)



考虑加载过程及桩体固结变形的碎石桩复合地基固结解析解*

郭彪①龚晓南②李亚军①

(①云南省交通规划设计研究院陆地交通气象灾害防治技术国家工程实验室昆明650041)(②浙江大学杭州310058)

为了完善碎石桩复合地基固结理论，通过假设从桩体排出的水量等于流入桩体的水量与桩体体积变化之和以及地基扰动区土体水平渗透系数呈线性变化，并考虑上部荷载逐渐施加，推导了考虑桩体体积变化的碎石桩复合地基超静孔压及固结度解析解。当加载时间趋于零时，本文解可退化为瞬时加载情况下的解； 当加载时间及桩径同时趋于零时，本文解可进一步退化为Terzaghi一维固结解，这证明了本文解的正确性。通过与已有解的比较，对地基固结性状进行了分析。结果表明，加载过程对地基固结度影响显著，加载历时越长，固结越慢； 在各种条件下，不考虑桩体固结变形时地基固结始终比考虑桩体变形时快，并且其影响随着加载历时变小、桩径比变小、桩土模量比变小、桩土渗透系数变小而逐渐增大，这说明在实际工程固结计算中不考虑桩体固结变形是偏于不安全的。

碎石桩复合地基固结加载过程桩体固结变形解析解

0　引　言

采用碎石桩处理软土地基是一种简单经济有效的措施，地基沉降是碎石桩复合地基的主要的问题之一，要对地基沉降进行分析，就必须研究复合地基的固结理论。

碎石桩复合地基和砂井地基相比，具有应力向碎石桩集中以及桩径比(碎石桩影响区半径与桩半径之比)较小的特点。与砂井地基相比，碎石桩复合地基固结理论研究起步较晚，研究较少。Yoshikuni(1979)最早提出了复合地基应力集中效应并引入到复合地基的固结理论研究中。此后，王瑞春等(2001， 2002， 2004)、Han et al.(2001， 2002)、孙举等(2008)、张玉国等(2005， 2014)众多学者对复合地基固结理论不断进行了研究完善，发展了未打穿复合地基、双层复合地基、变荷载、考虑碎石桩施工的扰动作用以及桩体渗流阻力作用、半透水边界等多种工况及影响因素下的碎石桩复合地基固结理论。

扰动区土体的水平渗透系数变化对复合地基固结有很大的影响，近年来在这方面有较多的研究。桩体周围扰动土体渗透系数随扰动作用强弱变化这一现象由Sharma et al.(2002)通过试验研究发现，此后，wlader Hal et al.(2002)、Zhang et al.(2006)、Xie et al.(2009)进行了进一步研究和完善，得到了水平渗透系数线性连续变化、二次抛物线形式连续变化等情况下的固结解。

不过在以上的理论中，均没有考虑碎石桩的竖向变形，假定某一时刻从桩体排出的水量就等于土体流入桩体的水量，这与理论所采用的等应变假设是不符的。于是卢萌盟(2009)、赵明华等(2010)针对这一点，通过对桩周流量假设进行改进考虑了桩体的竖向变形，从而解决了这一矛盾。

然而，在卢萌盟(2009)、赵明华等(2010)的研究中，假定外部荷载是瞬时施加的，这与工程实际不符，使得这一理论难以得到广泛应用。鉴于此，本文推导得到了变荷载下考虑桩体变形的复合地基固结解析解，并考虑地基涂抹区水平渗透系数呈线性变化，与现有解进行了比较验证，分析了地基固结性状。

1　固结方程及求解条件

图1为变荷载下碎石桩复合地基固结简化模型。图中re为碎石桩影响区半径，rs为涂抹区半径，rc为碎石桩半径，us、uc分别为土体及桩体内的超静孔压力，Es、Ec分别为土体及桩体的压缩模量，kr(r)为土体水平渗透系数，kv为土体竖向渗透系数，kc为碎石桩体渗透系数，H为碎石桩深度，q(t)为上部荷载。

除了桩土等应变假设以及达西定律，本文还作了以下假定： ①地基上部荷载是时间的函数，附加应力随深度不变； ②从桩体排出的水量等于从土体流入桩体的水量与桩体体积减小之和。

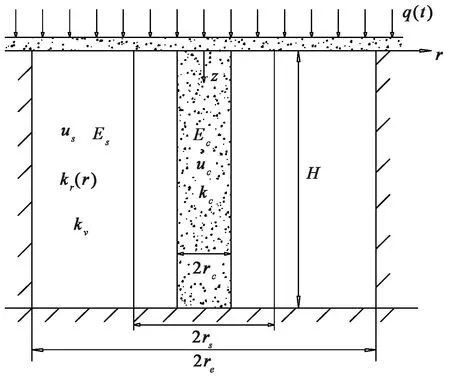
图1　碎石桩复合地基示意图Fig. 1　Sketch diagram of gravel pile composite foundation

根据谢康和(1993)，Xie et al.(2009)，Zhang et al.(2006)文献的研究，复合地基土体的固结方程可以写成：

(1)

其径向的边界条件为：

(2)

(3)

(4)

式(1)中， kr(r)为土体水平渗透系数，为随r变化的函数，其表达式为：

(5)

式(1)为一个多元多次偏微分方程，无法直接求解，需对其作进一步推导。

下面首先推导地基的应变εv的表达式：

复合地基上部荷载由碎石桩及土体共同承担，地基竖向的平衡方程为：

(6)

又根据等应变假设，即地基土体与桩体在任意时刻应变相等，有：

(7)

由式(6)、式(7)可得：

(8)

(9)

式(9)可以改写为：

(10)

将式(5)、式(8)带入式(1)可得：

(11)

接下来对式(11)进行消元推导：

对式(11)两边关于r积分并利用边界条件(2)可得：

(12)

再对式(12)两边关于r积分并利用边界条件(3)可得：

(13)

其中，

(14)

将式(10)带入式(13)后，再将式(13)带入式(4)可得：

(15)

其中，

(16)

(17)

本文假设从桩体排出的水量等于流入桩体的水量与桩体体积变化之和，在地基固结过程中，桩体的体积变化量ΔVc可以写成：

(18)

由达西定律，参考卢萌盟(2009)的研究，从桩体向上流出的水量Qvc的表达式为：

(19)

同时，从地基土体流入桩体的水量Qhs的表达式为：

(20)

故可得在dt时间段内桩体内水量的变化量ΔQc为：

(21)

由桩周流量假设可知ΔQc=ΔVc，将式(18)、式(21)带入整理可得：

(22)

(23)

由式(22)、式(23)有：

(24)

将式(8)、式(10)带入式(24)整理可得：

(25)

其中，

(26)

(27)

(28)

其中，

(29)

(30)

再结合式(25)和式(28)可得：

(31)

式(31)即为变荷载下考虑桩体变形的碎石桩复合地基固结控制方程，考虑顶面排水，底面不排水，其竖向边界条件为：

(32)

地基不同位置处土体水平向渗透系数的变化情况(图2)。图中kh为未受到碎石桩施工影响范围内的水平渗透系数，ks为受到施工影响最大处(紧临桩体)土体水平渗透系数。

图2　土体平渗透系数Fig. 2　Permeability coefficient in soil

本文描述渗透系数随r变化的函数f(r)形式为(卢萌盟， 2009)：

(33)

其中， δ=kh/ks。

由式(14)、式(16)、式(17)、式(33)可得：

(34)

式中， s=rs/rc。

2　方程求解

在实际工程，荷载逐渐施加的，加载至最终荷载后保持不变(图3)。式中，t1为加载到最终荷载所经历的时间，qu为最终荷载。

图3　荷载随时间变化图Fig. 3　Variation of preloading with time

荷载可表示为：

(35)

将上式代入式(31)可得：

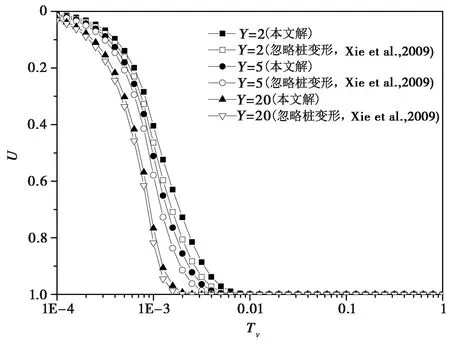
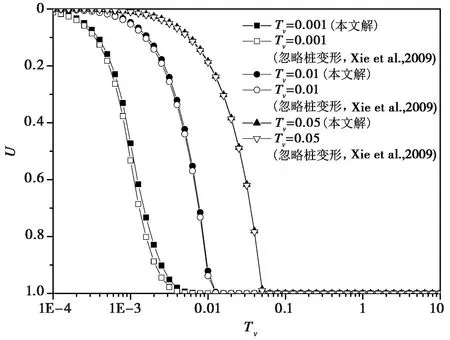
当0≤t

(36)

当t≥t1时：

(37)

设方程(36)的解为：

(38)

根据边界条件式(32)可解得：

从而可得：

(39)

式(39)代入式(36)可得：

(40)

在式(40)两端同乘以某一具体项sin(Mz/H)后在[0，H]上积分可得：

(41)

其中，

(42)

(43)

由初始条件可得：

(44)

在式(44)两端同乘以某一具体项sin (Mz/H)后在[0，H]上积分可得：

(45)

方程(41)和式(45)分别为关于Tm(t)的常微分方程以及初始条件，其解可写为：

(46)

将式(46)代入式(39)可得：

(47)

式(37)解的形式可写成：

(48)

其初始条件为：

(49)

由式(48)、式(49)可得：

(50)

将(50)代入式(48)可得：

(51)

综上所述，可得地基某时刻某深度处的平均孔压为：

当0≤t

(52)

当

(53)

将式(42)、式(43)代入式(53)并整理可得：

(54)

地基任一时刻的固结度为：

(55)

将式(35)、式(52)、式(54)代入式(55)可得：

0≤t

(56)

t≥t1时：

(57)

将系数A、B、C、D代入式(42)可得βm的表达式为：

(58)

3　解的验证及比较

为了验证本文解的合理性，将解进行退化。

在瞬时加载情况下，t1→0，式(54)退化为：

(59)

式(58)、式(59)即为卢萌盟(2009)的解。

进一步地，如n→∞，即桩的半径趋于0时，式(58)退化为：

(60)

式(59)、式(60)即为Terzaghi一维固结解。

上述退化结果表明，卢萌盟(2009)的解及Terzaghi一维固结解均为本文解的特例，本文解是合理正确的。

图4　本文解与卢萌盟(2009)解的比较Fig. 4　Comparison of the average degree of consolidation by the present solution and the Lu M M(2009) solution

图4是本文解与卢萌盟(2009)的解的比较，卢萌盟(2009)的解认为荷载瞬时施加。图中Tv1为t1时刻对应的地基竖向固结时间因子。计算参数为：n=4，s=2，H/rc=20，Y=5，kh/kv=2，kc/kh=500，δ=0.4。

从图可以看出，逐渐加载与瞬时加载固结度差别是巨大的，加载历时越长，固结越慢，在实际工程中，堆载都是逐渐施加的，本文解比卢萌盟(2009)解更加合理适用。

图5～图8 是本文解与Xie et al.(2009)的解的比较，在Xie et al.(2009)的解中考虑了加载过程以及涂抹区水平渗透系数呈线性变化，但没有考虑桩体的固结变形，通过与此解全面的比较可突出本文的研究成果。

图5是不同桩径比时两者固结速度的比较。计算参数为：Tv1=0.001，s=1.6，H/rc=40，Y=5，kh/kv=2，kc/kh=500，δ=0.4。从图可以看出，不考虑桩体变形时地基固结仍然比考虑桩体变形时快，可见在工程应用中不考虑桩体变形是偏不安全的，这会低估地基的工后沉降。不过随着桩径比的增大，两者的差异逐渐减小。

图6是不同桩土模量比时解的比较。计算参数为：Tv1=0.001，n=2，s=1.6，H/rc=40，kh/kv=2，kc/kh=500，δ=0.4。从图可以看出，不同桩土模量比下不考虑桩体变形时地基固结仍然比考虑桩体变形时快，随着桩土模量比的增大，两者的差异逐渐减小。

图7是不同桩土渗透系数比时解的比较。计算参数为：Tv1=0.001，n=2，s=1.6，H/rc=40，kh/kv=2，Y=2，δ=0.4。从图可以看出，不同桩土渗透系数比下不考虑桩体变形时地基固结同样比考虑桩体变形时快，随着桩土渗透系数比的增大，两者的差异逐渐减小。

图6　不同桩土模量比时与Xie et al.(2009)解的比较Fig. 6　Comparison with the Xie et al.(2009) solution under different compression modulus ratios of column and soils

图7　不同桩土渗透系数比时与Xie et al.(2009)解的比较Fig. 7　Comparison with the Xie et al.(2009)solution under different permeability coefficient ratios of column and soils

图8　不同加荷历时条件下与Xie et al.(2009)解的比较Fig. 8　Comparison with the Xie et al.(2009)solution under different loading time

图8是不同加载历时考虑桩体固结变形与不考虑时地基的固结速度比较。计算参数为：n=2，s=1.6，H/rc=20，Y=5，kh/kv=2，kc/kh=500，δ=0.4。从图可以看出，不考虑桩体变形时地基固结比考虑桩体变形时快，不过，加载速度越慢，两者的差距越小，但这样做会耽误工期，影响施工进度。

图9是本文解与王瑞春等(2002)的解的比较，在王瑞春等(2002)的解中考虑了加载过程，但没有考虑涂抹区水平渗透系数的变化以及桩体的固结变形。计算参数为：Tv1=0.01，s=2，H/rc=20，Y=10，kh/kv=2，kc/kh=500，δ=0.4。从图可以看出，考虑涂抹区水平渗透系数呈线性变化比不考虑要快，当桩径比n=5时两者差距较大，而当n=2时两者差距明显缩小，通过前面的分析可知，这是因为当桩径较小时，不考虑桩体固结变形对地基固结度影响较大，与不考虑涂抹区水平渗透系数变化两因素相抵所致。

图9　不同桩径比时与王瑞春等(2002)解的比较Fig. 9　Comparison with the Wang et al.(2002)solution under different diameter ratios

4　结　论

本文推导得到了变荷载下考虑桩体变形的复合地基固结解析解，解可退化到瞬时荷载下的解，并可进一步退化到Terzaghi解，说明本文解是正确的。

通过地基固结比较分析可知：

(1)逐渐加载与瞬时加载固结度差别显著，加载历时越长，固结越慢，本文考虑荷载施加过程，更加符合工程实际。

(2)考虑涂抹区水平渗透系数呈线性变化比不考虑要快。

(3)在各种条件下，不考虑桩体变形时地基固结始终比考虑桩体变形时快，并且其差值随着加载历时变小、桩径比变小、桩土应力比变小、桩土渗透系数变小而逐渐增大。

也就是说，不考虑桩体变形会高估地基的固结速度，从而低估地基的工后变形量。因此，在实际工程固结计算中不考虑桩体变形是偏于不安全的，本文解可使计算结果更符合实际。

Han J，Ye S L. 2001. Simplified method for consolidation rate of stone column reinforced foundations[J]. Journal of Geotechnical and Geoenvironmental Engineering，127(7)： 597～603.

Han J，Ye S L. 2002. A theoretical solution for consolidation rates of stone column-reinforced foundations accounting for smear and well resistance effects[J]. International Journal of Geomechanics，2(2)： 135～151．

Hawlader B C，Imai G，Muhunthan M. 2002. Numerical study of the factors affecting the consolidation of clay with vertical drains[J]. Geotextiles and Geomembranes，20(4)： 213～239．

Lu M M. 2009. Analytical Study on Consolidation Theory of Composite Ground under Complicated Conditions[D]. Hangzhou： Zhejiang University．

Sharma J S，Xiao D. 2002. Characterization of a smear zone around vertical drains by large-scale laboratory tests[J]. Canadian Geotechnical Journal，37(6)： 1265～1271．

Sun J，Xie X Y，Xie K H. 2008. Analytical theory for consolidation of double-layered composite ground with granular columns[J]. Rock and Soil Mechanics，29(2)： 321～326．

Wang R C，Xie K H. 2001. Analytical theory for consolidation of double-layered composite ground with granular columns[J]. Chinese Journal of Geotechnical Engineering，23(4)： 418～422．

Wang R C，Xie K H，Guan S H. 2002. Analytical solutions for consolidation of composite ground with granular columns under time-dependent loading[J]. Journal of Zhejiang University(Engineering Science)， 36(1)： 12～16．

Wang R C，Xie K H，Tang X W. 2004. Analytical study on consolidation of composite ground with partially penetrated granular columns[J]. Journal of highway and transportation research and development，21(6)： 12～16．

Xie K H. 1993. Research status and development of composite foundation consolidation theory[J]. Ground Improvement，4(3)： 1～14．

Xie K H，Lu M M，Hu A F，et al. 2009. A general theoretical solution for the consolidation of a composite foundation[J]. Computers and Geotechnics，36(1—2)： 24～30．

Yoshikuni H. 1979. Design and control of construction in the vertical drain method[M]. Tokyo： Gihoudou．

Zhang Y G，Xie K H，Ying H W，et al. 2005. Consolidation analysis of composite foundation of granular columns with impeded boundaries[J]. Chinese Journal of Geotechnical Engineering，27(3)： 304～307．

Zhang Y G, Xie K H，Wang Z. 2006. Consolidation analysis of composite ground improved by granular columns considering variation of permeability coefficient of soil[J]. Ground Modification and Seismic Mitigation， ASCE，Geotechnical Special Publication， GSP152： 135～142．

Zhang Y G，Sun M，Xie K H. 2014. Study of simplifying solution to consolidation of composite ground with partially penetrated granular columns[J]. Rock and Soil Mechanics，35(5)： 1303～1310．

Zhao M H，Liu D P，Zhang L. 2010. Analytical solution for consolidation of composite ground with granular columns accounting for consolidation deformation of pile[J]. Rock and Soil Mechanics，31(2)： 483～488．

卢萌盟. 2009. 复杂条件下复合地基固结解析理论研究[D]. 杭州：浙江大学．

孙举，谢新宇，谢康和. 2008. 双层散体材料桩复合地基固结理论[J]. 岩土力学，29(2)： 321～326．

王瑞春，谢康和. 2001. 双层散体材料桩复合地基固结解析理论[J]. 岩土工程学报，23(4)： 418～422．

王瑞春，谢康和，关山海. 2002. 变化荷载下散体材料桩复合地基固结解析解[J]. 浙江大学学报(工学版)， 36(1)： 12～16．

王瑞春，谢康和，唐晓武. 2004. 未打穿散体材料桩复合地基固结解析研究[J]. 公路交通科技，21(6)： 12～16．

谢康和. 1993. 复合地基固结理论研究现状与发展[J]. 地基处理，4(3)： 1～14．

张玉国，谢康和，应宏伟，等. 2005. 双面半透水边界的散体材料桩复合地基固结分析[J]. 岩土工程学报，27(3)： 304～307．

张玉国，孙敏，谢康和. 2014. 未打穿散体材料桩复合地基固结简化解研究[J]. 岩土力学，35(5)： 1303～1310．

赵明华，刘敦平，张玲. 2010. 考虑桩体固结变形的散体材料桩复合地基固结解析计算[J]. 岩土力学，31(2)： 483～488.

ANALYTICAL SOLUTION FOR CONSOLIDATION OF STONE COLUMN-REINFORCED FOUNDATIONS TAKING INTO ACCOUNT CONSOLIDA￣TION DEFORMATION OF PILE UNDER PROGRESSIVE LOADING

GUO Biao①GONG Xiaonan②LI Yajun①

(①National Engineering Laboratory for Land Transport Meteorological Disaster Control Technology， Broadvision Engineering Consultants， Kunming650041)(②Zhejiang University， Hangzhou310058)

For the sake of improvement of the composite foundations consolidation theory， an analytical solution is obtained for consolidation of stone column-reinforced foundations taking into account the consolidation deformation of pile under progressive loading. Column consolidation and deformation are considered with the following two assumptions：(1)the quantity of water flowing through the disturbed soil zone into the column is not equal to that flowing out from the column and (2)the difference between them is equal to the volume change of the column. In addition， the linear distribution pattern of the horizontal permeability of soil in the disturbed zone is also taken into account for the disturbance effect of columns construction on the surrounding soil. To prove the correctness of the solution， a discussion is performed in the article. If the loading time tends to zero， the obtained solution can be convert to the solution in the condition of constant load. Furthermore， if the loading time and the size of stone columns tend to zero at the same time， the obtained solution can be convert to the one-dimensional solution obtained by Terzaghi. In the end， the average degree of consolidation of a composite foundation is obtained and discussed. The results show that the influence of loading process on the consolidation is obvious. The consolidation rate under the linear distribution pattern of the horizontal permeability of soil in the disturbed zone is faster than the consolidation rate in the condition of constant permeability. The consolidation rate considering deformation of pile is slower than consolidation rate using traditional assumptions. So that it is unsafe to ignore deformation of pile. Furthermore， the differences increase gradually as the loading time， the radius ratio， the stress ratios and the permeability coefficient ratios decrease．

Stone column-reinforced foundations， Consolidation， Preloading process， Column consolidation， Analytical solution

10.13544/j.cnki.jeg.2016.03.010

2015-05-22;

2016-03-30.

云南省交通厅科技项目(2015(A)12)，云南省山间盆地高等级公路软基处置新技术研究资助.

郭彪(1982-)，男，博士，高级工程师，主要从事地基方面的研究工作. Email: gb25891775@163.com

TU472

A