基于Fluent网格变形的旋流器的形状优化
2016-08-18蒋明虎谭放金淑芹龙桂兰陈桂芹徐保蕊东北石油大学机械科学与工程学院黑龙江大庆68大庆采油三厂一矿黑龙江大庆山东华宸高压容器有限公司山东济南500
蒋明虎,谭放,金淑芹,龙桂兰,陈桂芹,徐保蕊(东北石油大学机械科学与工程学院,黑龙江 大庆 68;大庆采油三厂一矿,黑龙江 大庆 6;山东华宸高压容器有限公司,山东 济南 500)
研究开发
基于Fluent网格变形的旋流器的形状优化
蒋明虎1,谭放1,金淑芹2,龙桂兰2,陈桂芹3,徐保蕊1
(1东北石油大学机械科学与工程学院,黑龙江 大庆 163318;2大庆采油三厂一矿,黑龙江 大庆 163113;3山东华宸高压容器有限公司,山东 济南 250101)
目前,旋流器的流体结构优化主要局限于单参数的尺寸优化;大多采用多组网格分别模拟的方法;不仅费时,而且对于微小的尺寸变形常常难以操控。当旋流器的分离效率优化到一定峰值后,进一步提高则比较困难。为解决这一问题,提出了基于网格变形的形状优化方法。以旋流器的分离效率为目标,采用ANSYS Fluent的网格变形方法,优化了旋流器的外形结构,将旋流器的分离效率由原来的95.69%提高到了99.18%,并对比分析了优化前后的压降、速度和油相体积分布。研究结果表明:Fluent 网格变形器驱动网格节点的平滑变形,可以同时实现变形区域的结构参数的优化组合,以及优化迭代的自动化和智能化,具有良好的全局搜索能力和较强的鲁棒性;Fluent网格变形优化算法能够缩短CAD建模的时间,避免网格重构;可在单一尺寸优化的基础上,在一定范围内提高旋流器的分离效率。
形状优化;网格变形;分离效率;轴流式旋流器;目标函数
旋流分离器是利用离心加速度进行轻相和重相分离的高效分离设备,具有结构紧凑、分离效率高、节能环保、系统配件少、维修费用低等特点,广泛应用于石油、环保、化工、矿山、冶金等领域。其中,轴流式旋流器的分离效率更高且流场稳定[1],不易产生循环流和短路流,特别适合于含油率较低的油水混合液分离。
优化旋流器的结构参数、提高分离效率一直是研究人员面临的重大课题。近年来,研究人员采用CFD方法,对轴流式分离器的结构参数进行了一系列优化研究工作,并且取得了一定的研究成果。聂涛[2]、俞接成[3]等初步探讨了轴流式旋流器的速度、压力和分离效率;GONG等[4]模拟了不同螺旋角和导流叶片的轴流式分离器的分离性能;王云峰等[5]对实体锥段和多孔介质锥段的轴流式旋流器进行了模拟研究;宋民航等[6]优化了轴流式脱水型旋流器的溢流口结构和出口形式;蒋明虎等[7-9]模拟了轴流式分离器的速度分布和压降规律并进行了实验研究,探讨了含气量对分离器性能的影响,优选了气、液、砂三相分离器的处理量和分流比等操作参数;赵立新等[10-11]优选了轴流式油水分离器的入口结构以及处理量和分流比等操作参数;史仕荧等[12]优化了轴流式分离器的矩形切向开缝出油管的结构;黄龙等[13]对轴流式气液旋流器的速度分布规律与压降变化进行了数值模拟。以上文献均采用的是基于控制变量法的单一尺寸优化;运用该方法开展旋流器的结构优化研究已进行得比较深入,对于进一步提高旋流器的分离效率已几乎没有提升空间;况且,单一的尺寸优化对旋流器的局部外形难以准确控制。为此,采用ANSYS Fluent的网格变形的方法[14],以旋流器的分离效率为单一目标函数,对旋流器的流体结构进行了形状优化,进一步提高了旋流器的分离效率。
1 ANSYS Fluent的网格变形优化器
所谓优化就是在设计空间中寻找最佳的合理设计点。Fluent网格变形器(mesh morpher)恰是基于用户自定义的控制点的网格运动进行光滑地变形的[15];在无需过多的人工干预的情况下,智能地寻找最佳设计点,可以很好地解决形状优化问题[16-17]。ANSYS Fluent在用户设定的变形区域中,设计点是由“控制体”限定的一系列控制点来实现,由这些控制点操控指定区域(控制体)网格的光滑变形;依据优化器的不同,其变形原理基于径向基函数插值法[18]或张量积的伯恩斯坦多项式[19]。
Fluent网格变形器无需重新修改CAD模型和网格重构,节省了CAD建模和划分网格的时间,对网格类型和物理模型没有限制;不足之处是无法对重叠的区域同时进行变形,不支持任意形状的变形,不能单独用于多目标优化。
Fluent Mesh Morpher/Optimizer(MMO)一共内置6个优化器,分别是:The Compass Optimizer[20]、The NEWUOA Optimizer[21]、 The Simplex Optimizer[22]、The Torczon Optimizer[23]、The Powell Optimizer[24]和The Rosenbrock Optimizer[25]。其中,Compass优化器以目标函数的最小值为网格变形的调整方向,从一个给定的值开始,基于最小二乘法的原理[26],通过逐步改进控制点进行网格变形。本文主要采用Compass优化器进行优化。
2 模型尺寸及参数设置
2.1旋流分离原理
模拟采用的轴流式旋流分离器是经尺寸优化过的,其几何结构模型如图1所示;初始结构的主要参数:入口段长度L1=50mm,螺旋段长度L2=57mm,旋流腔长度L3=80mm,锥管段长度L4=336mm,尾管段长度L5=50mm,溢流管长度L7=16mm,旋流腔直径D2=50mm,底流口直径D4=25mm,溢流管直径D5=8mm,螺旋流道数N=5,锥管段锥角α=6°。其工作原理是,油水混合介质由入口进入螺旋流道产生强旋流,冲入旋流腔后继续作强螺旋流动,产生重力加速度几百倍以上的离心加速度。由于密度的差异,在离心力的作用下,水相流向壁面并汇集到底流口流出,而油相则被挤向旋流器的中心区域,形成细长状的油心,在背压的作用下从溢流口流出,从而实现油水分离。
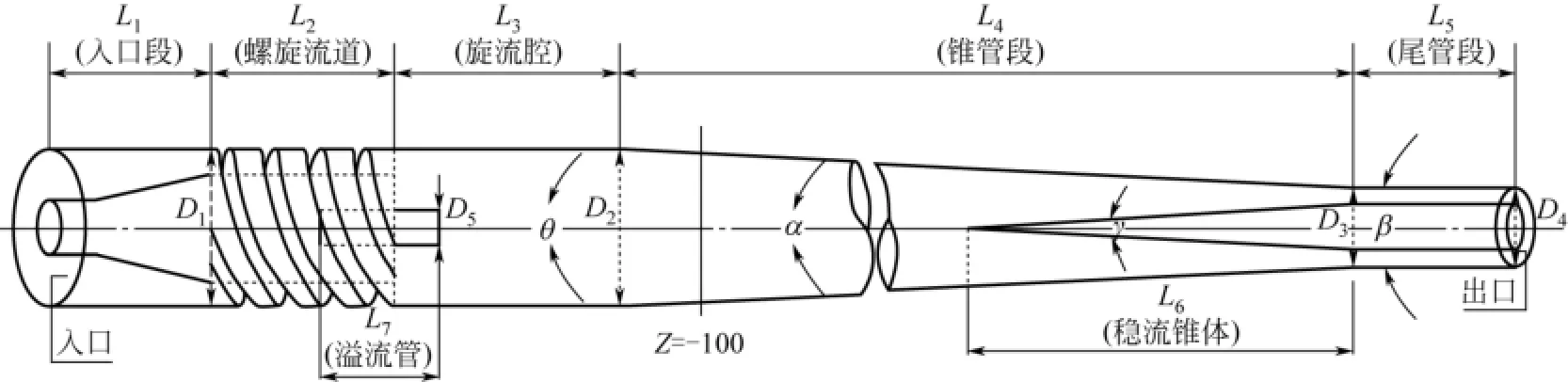
图1 旋流器初始结构模型
2.2网格划分
因六面体结构化网格数量较少,网格单元和流体流动方向对齐,既可以提高求解精度,又可以节约计算成本,特别适合于多相流的模拟计算;故采用ICEM CFD对旋流器进行全六面体网格划分。为检验网格的无关性,划分了3种不同数量的六面体网格单元;分别是390901个(分离效率为95.56%)、445188个(分离效率为95.69%)和852067个(分离效率为95.71%),网格质量均在0.3以上;因后两个分离效率模拟数据比较接近,考虑到节省计算资源,最终确定为 445188个六面体单元,413203个节点(如图2所示)。

图2 旋流器的网格划分
2.3参数设置
影响油水分离器分离性能的参数主要有:入口混合介质参数(油滴粒径、油和水的黏度、油水密度差和含油浓度等)、操作参数(入口流量、分流比等)和结构参数(旋流腔尺寸、锥管段尺寸、尾管段尺寸、入口尺寸、溢流管尺寸和螺旋流道尺寸等)。本文只改变旋流腔、锥管段及尾管段的形状和尺寸进行数值模拟,力求得到三者的最佳匹配参数。
油水混合介质的物性参数:水的密度为0.9982×103kg/m3,水的黏度为 1.003×103kg/(m·s),油的密度为889kg/m3,油的黏度为1.06kg/(m·s),油滴粒径为0.4mm。操作参数:环境温度为298K,环境压力为101325N/m2,入口速度为0.8m/s,底流分流比为80%,溢流分流比为20%,水相的体积分数为98%,油相的体积分数为2%。
就旋流器模拟方法而言,大涡模拟(large eddy simulation,LES)和雷诺应力(Reynolds stress model,RSM)模型最适合三维高旋流,但大涡模拟需要较高的网格质量且耗费的计算资源较多,而雷诺应力模型忽略了各项同性的涡黏性假设,较好地考虑了漩涡、旋转流动的变化情况,具有较强的模拟螺旋复杂湍流的能力,计算结果比较可信;又因为Mixture多相流模型能够考虑相间的速度滑移,故采用RSM模型和Mixture模型进行数值模拟。
模拟采用的是基于压力基的计算稳健的SIMPLE算法、双精度和二阶迎风格式;因计算域具有较大的曲率且为高旋流,故压力项设置为PRESTO!;残差精度设置为10-7,完全可以满足计算要求。为方便配置分流比,底流和溢流出口的边界条件均设置为 outflow。数值模拟设置如表 1所示。

表1 数值模拟设置
3 优化过程
3.1变形原理[27]
用于本文的网格变形原理基于伯恩斯坦多项式。若在一个坐标系内建立一个控制体,控制体内的坐标控制点被映射到网格节点上,由坐标控制点带动网格节点的运动。
假定q为网格内节点,其位移由局部三维控制点(uq,vq,wq)进行限定,在 l×m×n的控制体内,u、v、w分别与坐标 i、j、k方向相对应。第 q个网格节点位置与第i、j、k控制点位置之间的线性关系见式(1)。
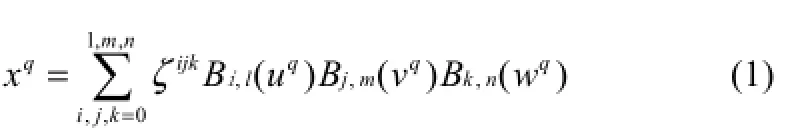
式(1)中,Bi,l(u)为第l阶伯恩斯坦多项式,见式(2)。)
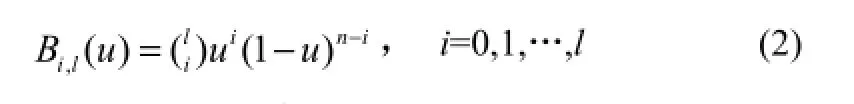
控制体内的网格变形是由一个或多个控制点的移动映射到网格节点来进行平滑定位的,由网格节点定位的目标函数δτ的变化可按式(3)、式(4)估算。
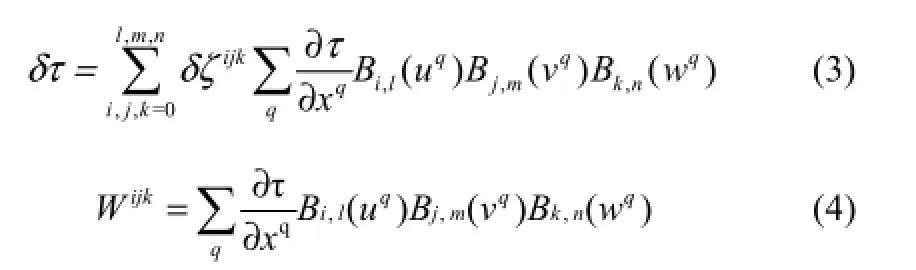
为控制点的敏感区域,δζijk表示控制点位置的调整。通过简单的梯度运算,令δζijk=λWi jk,即可求出光滑边界的网格形变,从而改进设计(式中比例系数λ默认值为1);增加网格数量和单元阶次都可以提高提高计算精度。
3.2变形优化过程
Fluent MMO的运行步骤如下:
(1)按照Fluent设置首先求得初始结构的模拟结果文件;
(2)加载MMO模块,依次设置变形体区域、网格变形方向和大小、目标函数、优化器、收敛精度及离散步数等;
(3)优化求解,Fluent软件会根据设定的精度自动智能开始优化计算,到达设计精度时运算终止。
因旋流腔、锥管段和尾管段(如图1所示)是影响旋流器的分离效率的主要结构参数[28];因此,在保持旋流器整体长度不变的情况下,取8个优化设计点,对这三部分进行结构变形优化,变形方向均为径向中心方向。网格变形控制体如图3所示。
网格变形体共得到49个,从中选取4个对称变形结构,如图4所示,可看出大致变形趋势。

图3 网格的变形控制体

图4 旋流器的网格变形过程
定义旋流器分离效率为式(5)。

式中,Ez为旋流器分离效率;m˙in为入口油相的质量流量,kg/s;m˙ov为溢流油相的质量流量,kg/s。以分离效率作为单一目标函数(如图 5所示),收敛精度设置为 0.001,由于溢流口的质量流量为负值,故优化目标就是力求目标函数值为最小。
目标函数的优化设计阶段如图6所示。图6中,目标函数曲线左端点为目标函数(分离效率)的初始值,右端点为最终优化值;在经过进行49次网格变形后达到所设定的计算精度,分离效率达到最大并趋于稳定。目标函数值越小分离效率越高,即曲线越靠近 x 轴分离效率越高。经计算,优化前旋流器的分离效率为95.69%,优化后的分离效率为99.18%,分离效率提高幅度较为明显。
4 结果分析
4.1形状变化
图7中(a)和(b)为变形前后的几何形状变化图,(c)为变形前后几何形状重叠图,透明部分为变形前的形状。从图7中可以看出,变形后得到的几何结构(旋流腔、锥管段和尾管段)较原来纤细,旋流腔和尾管段均由圆柱形变成圆台形,锥管段的锥角变小了。表2为几何变形前后各段锥角的变化情况。

图5 目标函数的设置

图6 目标函数的优化设计阶段
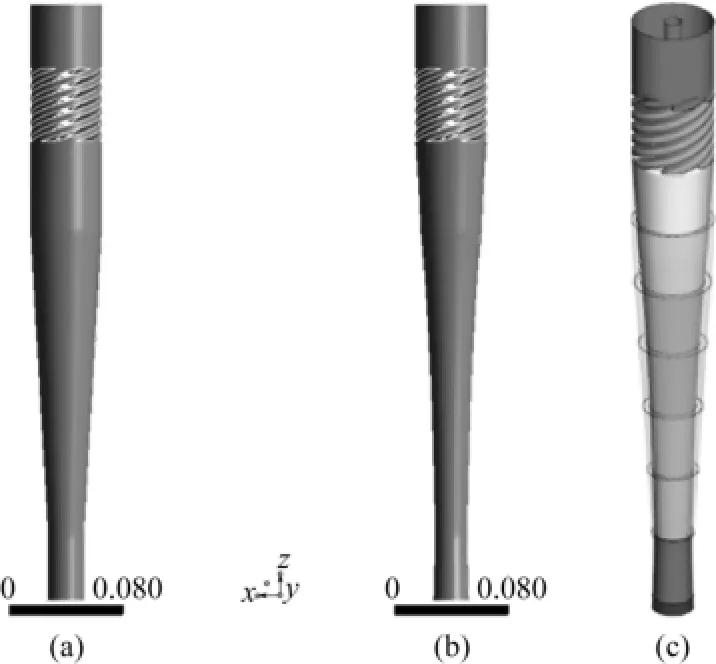
图7 变形前后的形状比较(单位:m)

表2 变形前后的锥角 单位:(°)
从以上数据可知,旋流器的几何形状的变化不大,优化后的旋流腔和锥管段平滑过渡并融为一体。这种几何形状的微小变化是传统的单一尺寸优化难以达到的。
4.2压降变化
由Fluent求解入口面、出口面及溢流口面的平均静压力及压降如表3所示。
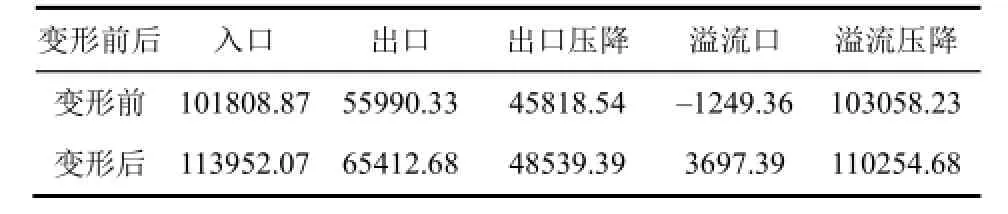
表3 平均压降变化 单位:Pa
由表3可知,变形后的压降均比变形前有所增大,但变化幅度均较小。变形前溢流口的压力为负值,对于溢流液的流出极为有利;由于流体压强的相互传递,变形后入口的压力增加了,溢流口的压力为虽为正值,但变化较小,约为7196.45Pa,对溢流液的流出影响不大。变形后的出口压降较变形前增加了,约为2720.85Pa,对于分离液的流出影响更小。图8为锥管段Z= -100mm处的变形前后静压力分布图,可知变形后混合液的压力有一定的损失,大约在104Pa数量级,约为0.1个大气压。
4.3速度变化

图8 变形前后的Z= -100mm处的压力
图9为锥管段截面Z= -100mm处的变形前后合速度对比图,可以看出,变形前后的图形基本形状未变,均为M形。变形后,外旋流的速度变大,内旋流的速度反而变小,二者的速度差有利于油水混合液的分离。

图9 变形前后的Z= -100mm处的合速度
切向速度决定旋流器中离心加速度和离心力的大小,是决定旋流器分离性能的重要因素[29]。图10为变形前后Z= -100mm处切向速度的变化图。由图10可知,变形前后的切向速度形状相似,且速度最大值重合;但变形后外旋流的速度变小且最值的差值较大,比变形前更靠近壁面;这种变化可促进油水分离,提高分离效率。
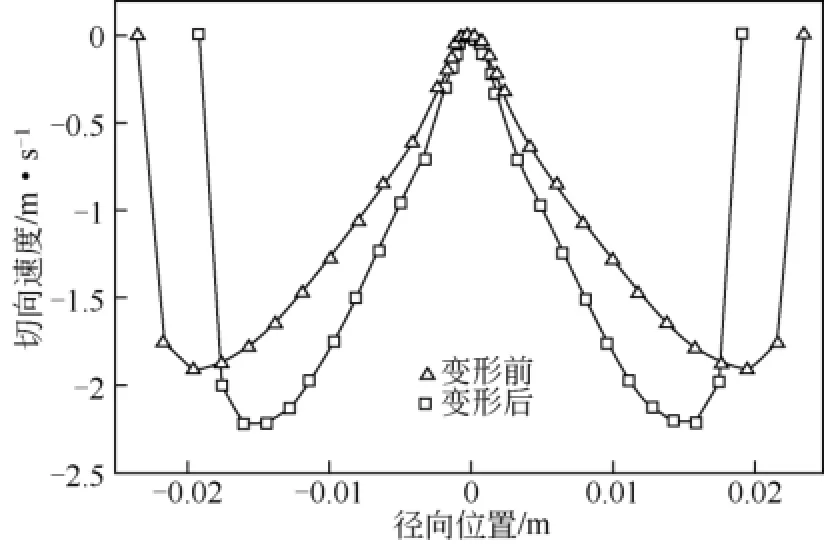
图10 变形前后的Z= -100mm处的切向速度
综合压降和速度变化可知,由旋流器几何形状的纤细改变而增加的旋流速度,是由增大的压降转化而来的;优化后的压力能比优化前降低较多,补充了油水分离所需要的动能,符合能量守恒定律,正是这种能量的转化提高了旋流器的分离效率。
4.4油相体积的变化
图11为油相体积的轴截面图。从图11中可以看出,在轴向中心和溢流口处,变形后的油心长度和宽度均比变形前的大,这说明油相的分布与变形前相比具有较大的体积分数,分离效率较变形前有所提高。
总之,经尺寸优化过的流体结构,再进行形状优化,分离效率仍有一定提升空间。分别改变网格的最小正交质量或选择不同的优化器(前文已提及,MMO共包含6个优化器),模拟结果是相同的;这说明MMO是稳健可靠的。

图11 变形前后油相的体积分数(单位:m)
5 模拟与实验对比分析
因入口流量为入口速度与入口截面积之积,为方便在实验[30]中控制流量,把入口速度0.7m/s、0.8m/s、0.9m/s、1.0m/s、1.1m/s换算为对应的进口流量,分别为5.0m3/h、5.7m3/h、6.4m3/h、7.1m3/h、7.8m3/h。
5.1分离效率的对比
图12为溢流分流比为0.2时,分离效率随入口流量变化的模拟与实验值对比图。由图12可知,随着流量的增大,分离效率有逐渐增加的趋势,但流量越大,分离效率增加的越缓慢且实验值均低于模拟值;当流量约为6.77m3/h时,变形后分离效率的实验值最高,超过7.1m3/h时,分离效率的实验值逐渐下降。这是因为实际分离过程中,随着流量的增加,剪切应力也随之增大,导致一部分油滴破碎,增大了油滴的乳化作用,致使分离效率降低。

图12 分离效率对比图
5.2压降的对比
图 13为变形后压降随入口流量变化的趋势对比图。
由图13可知,随着入口流量的增大,模拟和实验结果的压降也随之增大,溢流压降值均大于出口压降值;实验值均大于模拟值,这主要是旋流器实体结构制造质量的影响、模拟时对旋流器的壁面进行近似处理所致。

图13 压降对比图
6 结 论
(1)Fluent网格变形技术,可以在保证流体网格质量的前提下实现几何结构的平滑变形,避免受到几何重新建模和网格重新划分的制约。
(2)Fluent网格变形可以同时对控制体内的几何参数进行智能匹配,从全局角度系统地对结构参数进行目标驱动优化。优化过程是自动智能的,无需过多人工干预,具有很好的全局搜索能力。
(3)提高分离效率所需要的旋流速度,是由进口、出口和溢流口之间的压降来补偿的;压降的转化量是提高分离效率的基本前提。
[1]赵立新,宋民航,蒋明虎,等.轴流式旋流分离器研究进展[J].化工机械,2014,41(1):20-25.
[2]聂涛. 轴流式液液旋流器内流场的数值模拟[D]. 东营:中国石油大学(华东),2008:47-51.
[3]俞接成,陈家庆,韩景. 轴向入口油水分离水力旋流器及其数值模拟[J]. 北京石油化工学院学报,2009,17(2):19-23.
[4]GONG Guangcai,YANG Zhouzhou,ZHU Shaolin. Numerical investigation of the effect of helix angle and leaf margin on the flow pattern and the performance of the axial flow cyclone separator[J]. Applied Mathematical Modelling,2012,36(8):3916-3930.
[5]王云峰,刘仁桓,王金花,等. 2种锥段结构的轴流式旋流器内的流场模拟[J]. 流体机械,2013,41(6):22-26.
[6]宋民航,韩佳轩. 轴流式脱水型旋流器的流场分析与结构优化[J].石油矿场机械,2012,41(12):56-60.
[7]蒋明虎,陈世琢,李枫,等. 紧凑型轴流式除油旋流器模拟分析与实验研究[J]. 油气田地面工程,2010,29(9):18-20.
[8]蒋明虎,宫磊磊,徐保蕊,等. 含气条件对井下油水分离旋流器性能影响的数值模拟[J]. 化工机械,2014,41(5):629-632.
[9]蒋明虎,李永山,徐保蕊,等. 轴流式脱气除砂三相旋流分离器操作参数优选[J]. 化工机械,2015,42(1):68-71.
[10]赵立新,代佳鑫,郭现臣. 叶片式水力旋流器操作参数优选[J]. 流体机械,2013,41(10):7-9.
[11]赵立新,宋民航,蒋明虎,等. 新型轴入式脱水型旋流器的入口结构模拟分析[J]. 石油机械,2013,41(1):68-71.
[12]史仕荧,吴应湘,许晶禹,等. 导流片型管道式分离器油水分离结构优化[C]//第十三届全国水动力学学术会议暨第二十六届全国水动力学研讨会,青岛,2014:1063-1067.
[13]黄龙,邓松圣,王斌,等. 新型轴流导叶式气液旋流器流场数值模拟[J]. 机床与液压,2015,43(1):164-167.
[14]杨磊,李宝军,胡平. 网格变体方法的工程应用与进展综述[C]//中国计算力学大会2014暨第三届钱令希计算力学奖颁奖大会,贵阳,2014.
[15]BIANCOLINI Marco Evangelos. Mesh morphing accelerates design optimization[E/OL]. Rome,Italy,2010. http://www.ansys.com/ staticassets/ANSYS/staticassets/resourcelibrary/article/AA-V4-I1-Mesh-Morphing-Accelerates-Design-Optimization.pdf.
[16]JEMCOV Aleksandar,MARUSZEWSKI Joseph. Shape optimization based on downhill simplex optimizer and free-form deformation in general purpose CFD code[C]// 17th Annual Conference of CFD Society of Canada,Ottawa,Ontario,Canada,2009.
[17]MURUGAN S,WOODS B K S,FRISWELL M I. Hierarchical modeling and optimization of camber morphing airfoil[J]. Aerospace Science and Technology,2015,42(2):31-38.
[18]BIANCOLINI Marco Evangelos. Advanced mesh morphing for automotive applications using RBF Morph[C]//Automotive Simulation World Congress,Frankfurt am Main,Germany,2013.
[19]RAIDL Günther R,WUTM Christian. Approximation with evolutionary optimized tensor product Bernstein Polynomials[A]. Karlsplatz 13,1040 Vienna,Austria,2003.
[20]KOLDA Tamara G,LEWIS Robert Michael,TORCZON Virginia. Optimization by direct search:new perspectives on some classical and modern methods[J]. SIAM Review,2003,45(3):385-482.
[21]ZASLAVSKI Alexander,POWELL M J D. The NEWUOA software for unconstrained optimization without derivatives[M]. US:Springer,2004:255-297.
[22]MCKINNON K I M. Convergence of the Nelder-Mead simplex method to a nonstationary point[J]. SIAM J. Optimization,1998,9 (1):148-158.
[23]TORCZON Virginia. On the convergence of the multidirectional search algorithm [J]. SIAM J. Optimization,1991,1(1):123-145.
[24]PRESS William H,TEUKOLSKY Saul A,VETTERLING William T. Numerical recipes:the art of scientific computing[M]. 3rd Ed. Cambridge,England:Cambridge University Press,2007.
[25]ROSENBROCK H H. An automatic method for finding the greatest or least value of a function[J]. Computer Journal,1960,3(3):175-184.
[26]王仁芳,许秋儿,汪沁,等. 基于最小二乘网格的模型变形算法[J].计算机辅助设计与图形学学报,2010,22(5):777-783.
[27]ELSAYED Khairy. Design of a novel gas cyclone vortex finder using the adjoint method[J]. Separation and Purification Technology,2015,142:274-284.
[28]OLSONT T J,VAN OMMEN R. Optimizing hydrocyclone design using advanced CFD model[J]. Minerals Engineering,2004,17(5):713-720.
[29]袁惠新,李双双,付双成,等. 三相分离旋流器内流场及分离性能的研究[J]. 流体机械,2015,43(1):28-32.
[30]盛庆娇. 新型螺旋入口水力旋流器模拟分析及实验研究[D]. 大庆:东北石油大学,2012:39-45.
Sharp optimization of hydrocyclone based on Fluent mesh morphing
JIANG Minghu1,TAN Fang1,JIN Shuqin2,LONG Guilan2,CHEN Guiqin3,XU Baorui1
(1School of Mechanical Science and Engineering,Northeast Petroleum University,Daqing 163318,Heilongjiang,China;2The First Oil Mine,Daqing No.3 Oil Production Company,Daqing 163113,Heilongjiang,China;
3Shandong Huachen High Pressure Vessel Co.,Ltd.,Ji'nan 250101,Shandong,China)
Currently,fluid-structure optimization of hydrocyclone has been mainly limited to single-parameter size optimization. Generally,the optimization process is dependent upon the method of separate simulation with multiple sets of grid. Nevertheless,the approach is time-consuming and not capable of controlling the micro size deformation. Besides,further improvement on the separation efficiency of cyclone is rather difficult once a certain maximum optimization is achieved. To solve this problem,mesh deformation-based shape optimization method was proposed. Aimed at improving the hydrocyclone separation efficiency with ANSYS Fluent mesh deformation method,the hydrocyclone sharp structure was optimized and the hydrocyclone separation efficiency was increased from 95.69% to 99.18%. A comparative analysis involved with pressure drop,velocity and oil phase volume distributions before and after optimization was then conducted. The results indicated that the smoothing mesh deformation driven grid nodes by Fluent mesh morpher could concurrently contribute to the optimal combination of structural parameters in the deformation zone,and the optimization of the automation and intelligentization of the iteration process. Besides,it had a considerable capability ofglobal searching and strong robustness. Fluent mesh morphing optimization algorithm can shorten CAD modeling time,avoid mesh reconstruction and further improve the separation efficiency of hydrocyclone within a certain range on the basis of single-parameter size optimization.
sharp optimization; mesh morphing;separation efficiency;axial cyclone;objective function
TQ 028.4
A
1000-6613(2016)08-2355-07
10.16085/j.issn.1000-6613.2016.08.08
2016-02-18;修改稿日期:2016-03-11。
国家高技术研究发展计划(2012AA061303)。
及联系人:蒋明虎(1962—),男,教授,博士生导师,主要研究方向为旋流分离技术。E-mail jmhdq@126.com。
