基于改进协方差控制的传感器管理算法*

吕鹏飞，彭冬亮，左　燕，谷　雨

（杭州电子科技大学，杭州　310018）

基于改进协方差控制的传感器管理算法*

吕鹏飞，彭冬亮，左燕，谷雨

（杭州电子科技大学，杭州310018）

针对传统的基于协方差控制的传感器管理算法使用全遍历方法所造成的计算量大，以及传感器切换频繁的问题，提出了一种基于改进协方差控制的传感器管理算法。该算法在每一时刻首先判断前一时刻所用传感器组是否能够满足目标跟踪需求，以滤波协方差与期望协方差的偏差作为参考，结合量纲变换和特征值求取，为协方差偏差矩阵经过量纲变换后得到的量纲一致阵的所有特征值设定一个精度阈值，然后判断滤波协方差是否满足期望，从而决定是否维持当前选择的传感器组。在目标作匀速、匀加速、协同转弯等多种场景下进行了算法性能测试分析，仿真结果表明，该算法不仅在大部分场景下满足目标跟踪精度，而且能够提高传感器管理算法的实时性，同时降低传感器的切换频率。

传感器管理，协方差控制，目标跟踪精度，量纲变换

0　引言

在信息融合系统中，为目标跟踪配置更多的传感器资源，可以增加融合的可靠性，进而提高跟踪效果。但由于实际环境下的很多约束条件，能够提供的传感器资源往往十分有限，因此，为了充分发挥融合系统的功能及性能，需要对这些有限的传感器资源进行科学合理的分配［1］。传感器管理，指的是在一个传感器系统满足各项约束并达成运行目标时，对它的自由度进行控制［2］。为此，典型的是找到一个策略来决定每一时刻的最优传感器配置。

目前常见的传感器管理方法主要有基于规划论［3］、基于信息增益［4］和基于协方差控制［5-6］等方法。但它们普遍都存在一个问题，即每一时刻全遍历所有传感器组合造成的计算量大以及传感器频繁切换的问题。快速启发式算法［7］基于信息增益给所有传感器作了一个先验的排序，在线选取最接近期望增益的传感器组合，在一定程度上减少了算法的计算量和传感器的切换，但始终按传感器的排序依次增加传感器的方法使算法常常选择到不合适的传感器，既造成了传感器资源的浪费,还损失了跟踪精度。

针对传统的协方差控制方法中全遍历选择传感器组的方法所带来的计算量大以及传感器频繁切换的问题，本文在每一决策时刻利用前一时刻的传感器分配结果进行滤波，对滤波协方差与期望协方差的偏差进行量纲归一化再求取其特征值，并为这些特征值设定一个精度阈值，对其是否满足跟踪精度需求作出判断：若满足，则维持当前传感器选择；若不满足，则在该传感器组合的基础上增加或者减少其中的传感器。本文算法能够在不影响跟踪精度的前提下，降低算法的计算量及传感器组的切换频率。

1　基于协方差控制的传感器管理算法

基于协方差控制的传感器管理算法主要是以滤波估计协方差作为参考，每一时刻通过遍历所有组合来根据当前的观测值预测所有组合的滤波估计协方差，选择一组拥有与期望协方差最接近的滤波估计协方差的组合作为当前时刻的跟踪滤波组合［8］。其最优的目标函数为［9］：

式中：pi（tk）为第i种传感器组合Di在tk时刻的滤波估计协方差；pd（tk）为对应的期望协方差；f（·）为某种矩阵度量；Dopt（tk）表示当前时刻最优的传感器分配组合。

基于协方差控制的传感器管理算法可以在维持目标期望跟踪状态的条件下，合理分配传感器资源，但该算法也存在一些不足［10］：

1）算法在每一时刻通过遍历所有组合来进行最优组合的选择，对于有N个传感器的组网系统，传感器的组合就有2N-1个，计算量大，实时性差。

2）各时刻在最优组合的选择上并无关联性，因此，前后时刻使用的传感器组常常不同，这样频繁地切换传感器组合会在一定程度上造成系统的负担。

2　基于改进协方差控制的传感器管理算法

基于改进协方差控制的传感器管理算法的基本思想为：首先在第一时刻遍历所有组合，并以滤波协方差与期望协方差的偏差f（Pd（t1），pi（t1））最小为准则选取最优传感器组合；然后在之后的每一时刻tk开始时，用前一时刻的传感器组对目标进行观测，通过期望协方差与所得到的滤波估计协方差的差值矩阵ΔP=Pd（tk）-pi（tk）判断是否满足跟踪精度需求，若满足则维持当前的传感器组选择，若不满足则在当前传感器组的基础上增加或减少一个传感器。

基于改进协方差控制的传感器管理算法流程如图1所示。

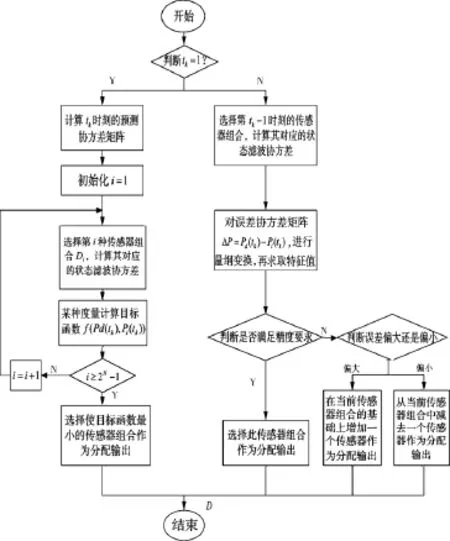
图1　基于改进协方差控制的传感器管理算法框图

该算法中，一方面采用基于协方差控制的传感器管理算法，在初始时刻为目标分配了一组最合适的传感器，保证了协方差的控制；另一方面，在后续的决策时刻无需重新分配传感器，而是利用前一时刻的传感器分配结果，快速确定一组能够有效跟踪目标的传感器组合。

2.1跟踪精度判断

在基于协方差控制的传感器管理算法中，传感器的选择是基于期望协方差与滤波估计协方差之间的偏差矩阵而决定的，即：

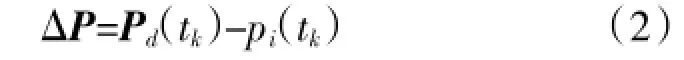
所以跟踪精度也是由此协方差偏差矩阵来判断。若该矩阵表明各误差均小于期望值，则可以判定满足跟踪精度的要求。

一般设定的期望协方差Pd（tk）为对角阵，而经过滤波过后的滤波协方差pi（tk）则往往不是对角阵，易见偏差协方差ΔP也不是对角阵，所以直接对其对角线上的元素进行判断就会忽视它的部分信息，因而可以通过对其求特征值来进行判断［11-12］。

不论是滤波协方差Pi（tk），还是期望协方差Pd（tk），在几何平面上都可以用一个椭圆来表示。协方差矩阵的特征值是椭圆的主轴和若干次轴长度的一半，特征向量表示这些轴的方向。

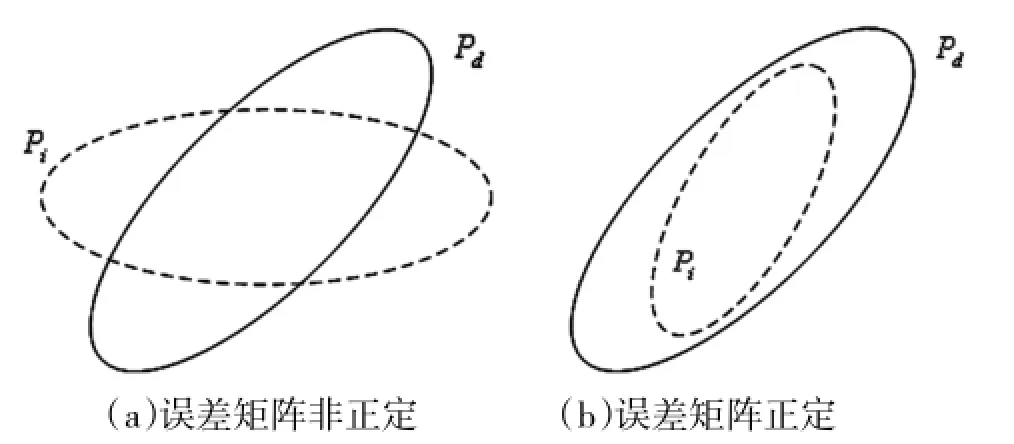
图2　滤波协方差所表示的各元素的误差

如图2所示，当偏差矩阵ΔP为正定矩阵，亦即其所有特征值均为正时，可以直观地看出滤波协方差所表示的各元素的误差均小于期望值，而当ΔP非正定时，则无法作出此判断。

为了在不影响跟踪精度的前提下尽量降低计算量和切换频率，本文为偏差矩阵特征值的判断设定了一个接近于零的上下限阈值。即使特征值不全为正，但只要它们均在零附近的一个较小的范围内，亦可认为满足精度需求。当特征值过大时，表示误差远远小于期望值，则可以从当前传感器组中减少一个传感器再进行观测；同理，当特征值过小时，可以增加一个传感器。

2.2量纲变换

协方差矩阵中各元素的量纲是不同的，例如，如果目标状态向量中包含位置（单位：m）和速度（单位：m/s），则滤波协方差矩阵的量纲为：

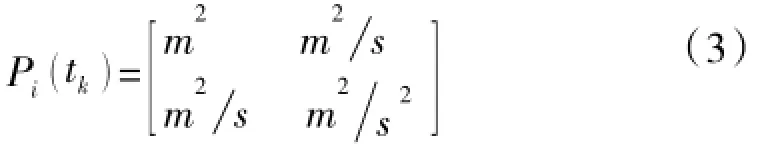
因此，在使用矩阵度量进行协方差比较时需要考虑量纲问题，而为了给协方差偏差矩阵的所有特征值设定一个统一的精度阈值，也需要对偏差矩阵进行量纲归一化。

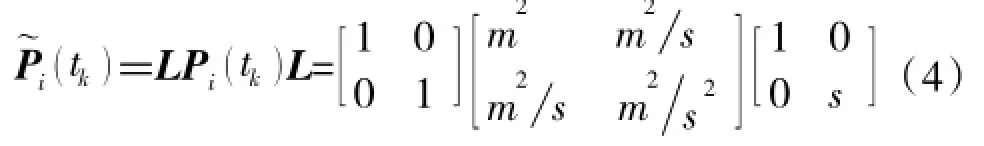
除了量纲阵变换，还有一种无量纲变换方法［14］。设和分别为期望协方差矩阵Pd（tk）的对角线元素，那么进行无量纲变换如下：

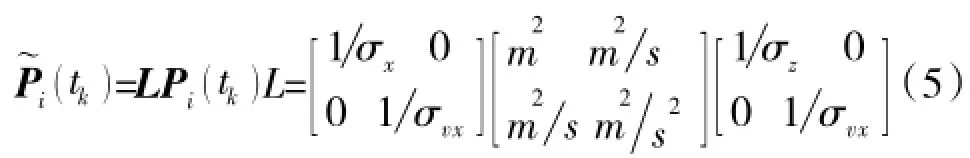
另一种解决量纲不一致问题的方法是，仅按位置期望协方差控制或仅按速度期望协方差控制，即每次计算时，从实际协方差中提取出位置或速度项进行比较。

3　仿真分析

3.1性能评估指标

本文对改进协方差控制方法和传统的全遍历协方差控制方法以及快速启发式方法进行比较，并以跟踪精度、传感器组切换率、传感器资源使用率以及计算量作为评价算法性能的指标。

跟踪精度，本文采用的是传感器滤波估计状态与目标实际状态之间的位置均方误差；传感器组切换率，是指在整个仿真过程中，传感器组切换的次数与总共选择传感器的次数的比值；传感器资源使用率，指的是使用的传感器占总的传感器资源的比例；计算量由仿真运行的时间表示。

位置均方误差：

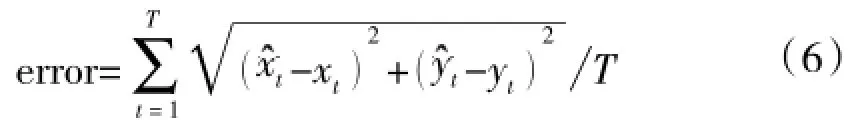
传感器组切换率：

其中Nc表示相邻时刻使用的传感器组不同的次数，Ns是对传感器组进行选择的总次数。

传感器资源使用率：

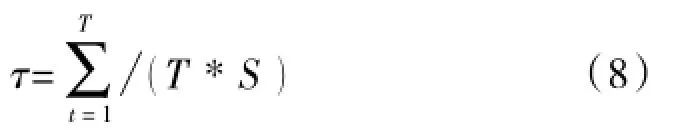
其中St表示每一时刻选择的传感器个数，S表示传感器总个数。

3.2仿真结果

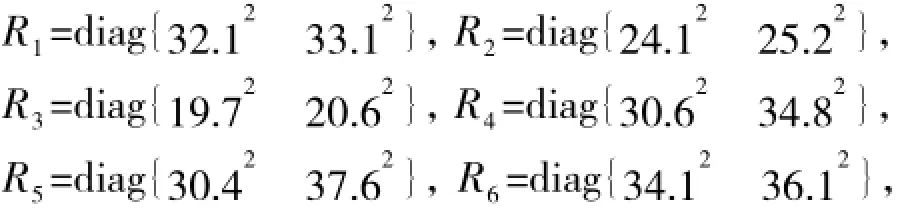
仿真场景1：目标运动模型为CV模型。

该场景下目标初始状态为x= ｛1000 200 1500 150｝T，运动过程中受到零均值高斯白噪声的扰动。考虑到初始时粗略跟踪，后期精确跟踪，将期望协方差设定为两阶段变化，前半段较大，为Pd1=diag｛ 26.8 4.4 71 4.7｝，后半段较小，为Pd2=diag｛ 26.8 3.3 30.6 3.5｝，采用无量纲变换，精度阈值前半段为0.74，后半段为0.61。

将本文提出的基于改进协方差控制的传感器管理算法与传统的全遍历协方差控制算法［5］以及快速启发式算法［7］进行比较，仿真结果如图3和图4所示。

3种算法各评价指标如表1所示。

图3　场景1：3种算法位置均方误差

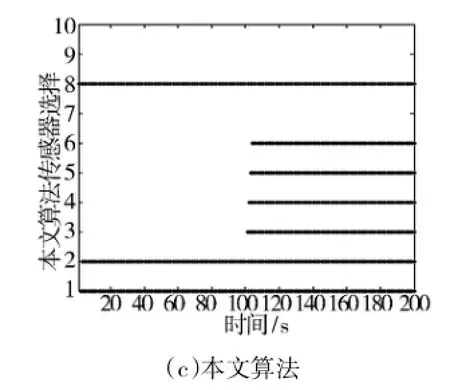
图4　场景：3种算法传感器选择情况

表1　场景1：3种算法性能评价指标

从上述图表中可以看出，当目标的运动模型为CV模型时，传统全遍历方法明显的缺点就是计算量大以及传感器切换频繁；快速启发式算法虽然减小了计算量和传感器切换率，但却浪费了过多的传感器资源，同时还损失了跟踪精度；本文算法因为在最开始就选择了最合适的传感器并且在后续时刻没有较大改变，所以能够保持较好的跟踪精度，并且在减小计算量和传感器切换率上比快速启发式算法更加有效。

仿真场景2：目标运动模型为CA模型。

该场景下目标运动模型CA模型，初始状态x= ［1 000 200 5 1 500 150 5］T，期望协方差前半段为Pd1=diag ｛60 5.4 0.007 705.70.007｝，后半段为Pd2=diag ｛29.3 4.3 0.004 344.50.0 0 4｝，采用无量纲变换，精度阈值前半段为0.8，后半段为0.7。

将本文提出的基于改进协方差控制的传感器管理算法与传统的全遍历协方差控制算法以及快速启发式算法进行比较，仿真结果如下页图5和图6所示。

3种算法各评价指标如下页表2所示。

从图表中可以看出，当目标的运动模型为CA模型时，快速启发式算法损失的跟踪精度非常大，而本文算法依然能够在很好地保持跟踪精度和传感器资源使用率的前提下，降低传感器组的切换率和算法的计算量。

仿真场景3：目标运动模型为CT模型。

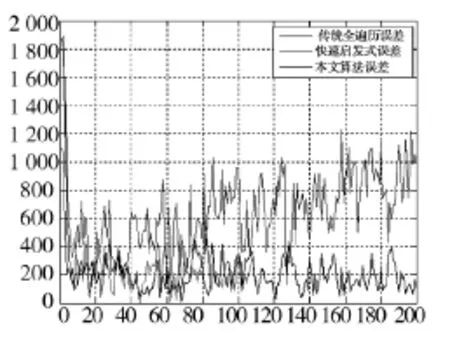
图5　场景二：3种算法位置均方误差

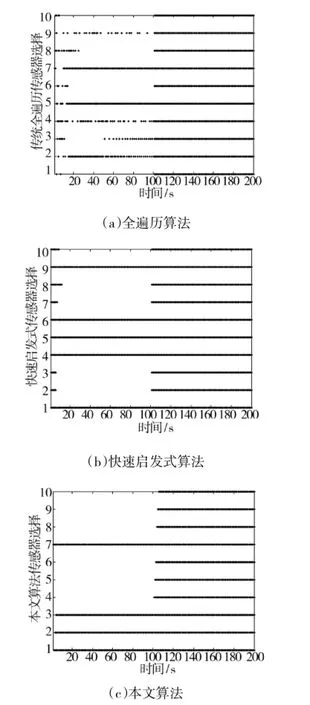
图6　场景2：3种算法传感器选择情况

该场景下目标的初始状态为x=［1 000 200 5 1 500 150 5］T，目标在整个过程中的角速度变化如表3所示。

对应于角速度变化的4个时段，将期望协方差也设定为四阶段变化，分别是Pd1= diag｛ 80.65.8092.560｝，Pd2= diag｛ 70.75.60805080｝，Pd3= diag｛ 605.350705.60｝，Pd4= diag｛46 4.9 0 525.10｝，采用无量纲变换，相应阶段的精度阈值分别为 0.77、0.69、0.66、0.64。

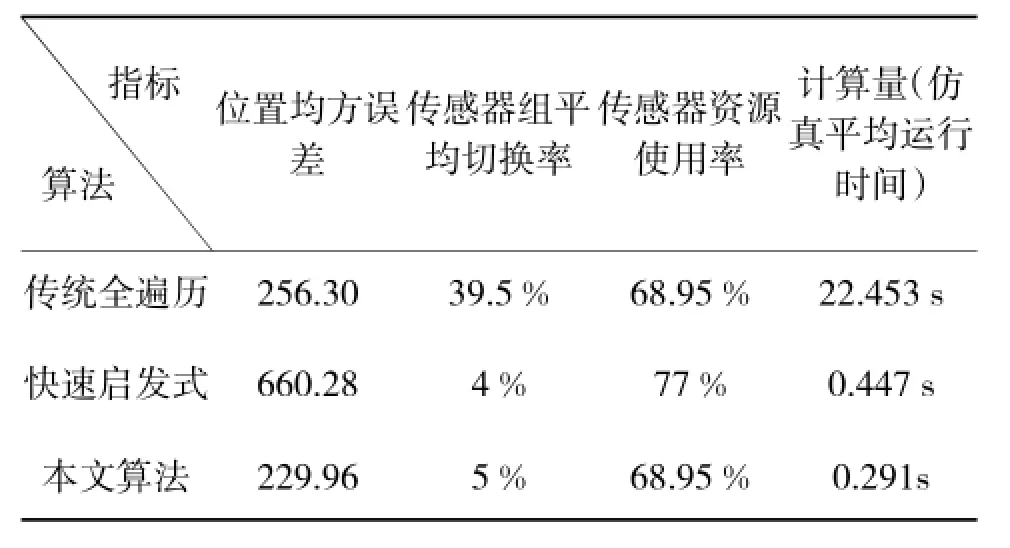
表2　场景2：3种算法性能评价指标

表3　场景3：目标角速度

将本文提出的基于改进协方差控制的传感器管理算法与传统的全遍历协方差控制算法，以及快速启发式算法进行比较，仿真结果如图7～图9所示。

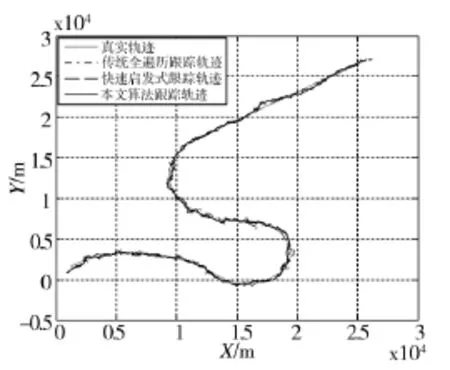
图7　场景3：目标实际运动轨迹与滤波曲线

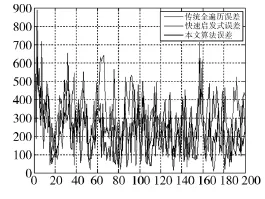
图8　场景3：3种算法位置均方误差

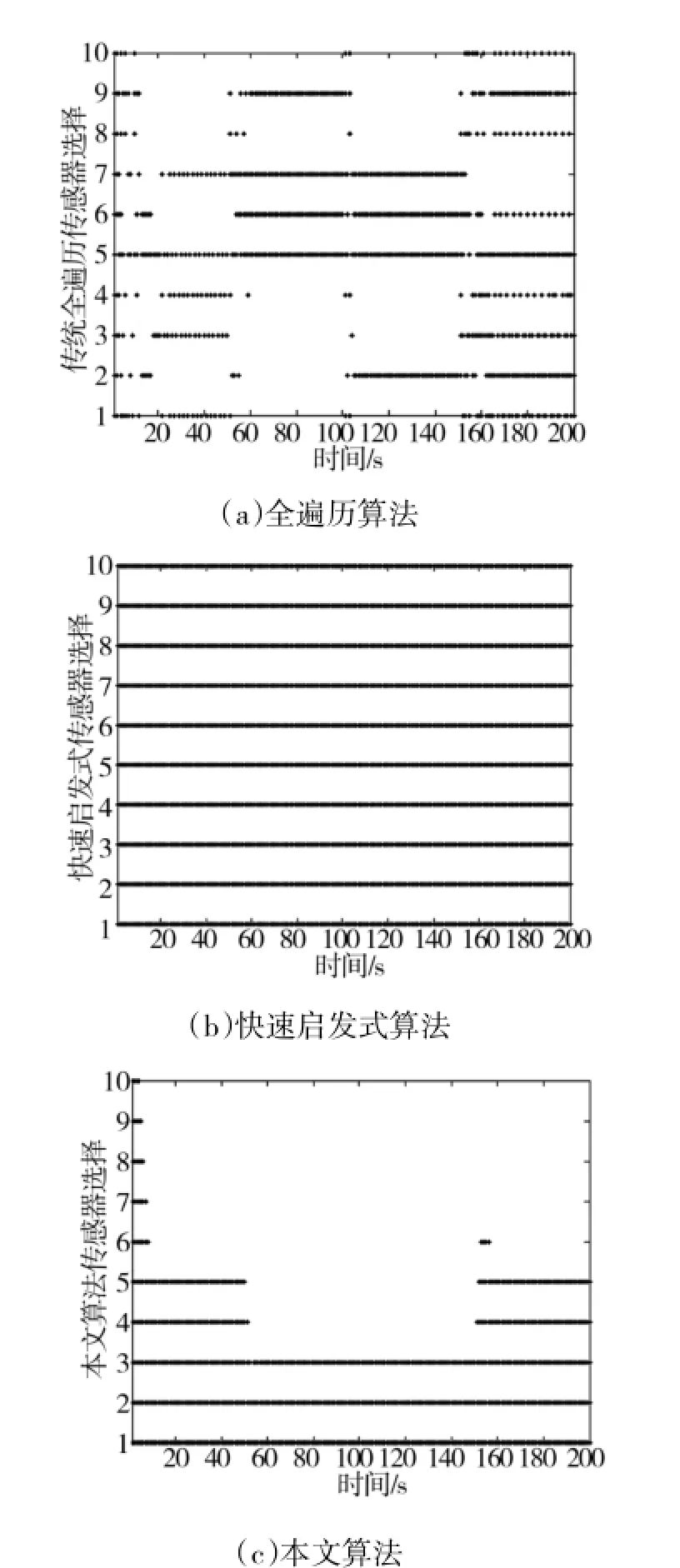
图9　场景3：3种算法传感器选择情况

3种算法各评价指标如表4所示。

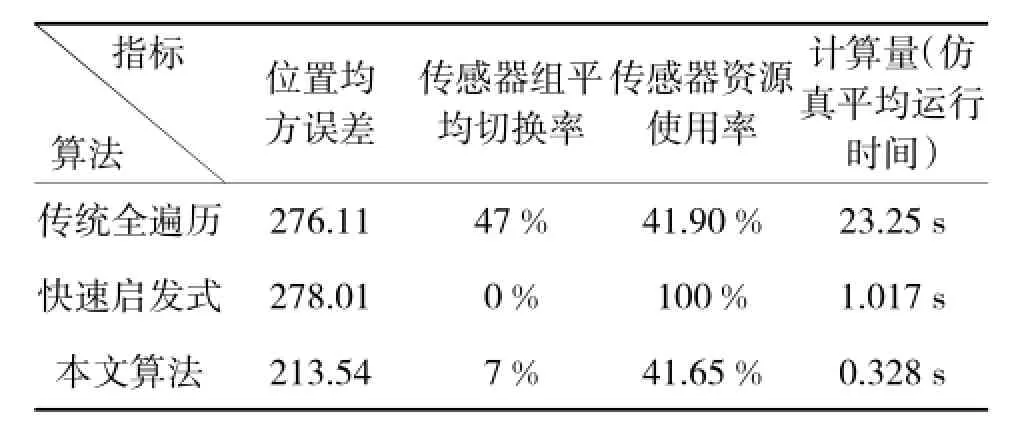
表4　场景3：3种算法性能评价指标

从上述图表中可以看出，当目标的运动模型为CT模型时，快速启发式算法由于目标速度和加速度的变化因而不能很好地进行协方差的控制，导致全时段都使用了所有的传感器，这显然是不好的；虽然加入了一定的机动情况，本文算法依然能够对目标进行快速有效的跟踪，并且提高算法的效率和实时性。

4　结论

本文在分析了协方差控制传感器分配问题的基础上，重点阐述了基于改进协方差控制的传感器管理算法，给出了整个算法流程。该算法相比于传统的全遍历协方差控制的传感器管理算法和多传感器选择快速启发式算法，在目标作匀速、匀加速以及协同转弯等多数场景下，保持了目标的跟踪精度，能够对目标进行有效跟踪，同时降低传感器管理算法的计算量和传感器的切换频率，有更好的效率和实时性。

［1］刘先省，申石磊，潘泉.传感器管理及方法综述［J］.电子学报，2002，30（3）：394-398.

［2］HERO A O，COCHRAN D.Sensor management：past, present,and future［J］.Sensors Journal，IEEE，2011，11 （12）：3064-3075.

［3］XIONG N，SVENSSON P.Multi-sensor management for information fusion：issues and approaches［J］.Information fusion，2002，3（2）：163-186.

［4］刘先省，周林，杜晓玉.基于目标权重和信息增量的传感器管理方法［J］.电子学报，2005，33（9）：1683-1687.

［5］周文辉，胡卫东，余安喜,等.基于协方差控制的集中式传感器分配算法研究［J］.电子学报，2004，31（B12）：2158-2162.

［6］周文辉，胡卫东，郁文贤.自适应协方差控制的传感器分配算法［J］.信号处理，2005，21（1）：57-62.

［7］徐松柏，左燕，谷雨.雷达组网多传感器选择快速启发式算法［J］.杭州电子科技大学学报，2014，34（2）：32-35.

［8］杨秀珍，何友，鞠传文.基于跟踪精度控制的传感器管理方法研究［J］.电光与控制，2005，12（1）：9-11.

［9］卢建斌，胡卫东，郁文贤.基于协方差控制的相控阵雷达资源管理算法［J］.电子学报，2007，35（3）：402-408.

［10］KALANDROS M，PAO L Y.Controlling target estimate covariance in centralized multisensor systems［C］//American Control Conference，1998.Proceedings of the 1998.IEEE，1998，5：2749-2753.

［11］KALANDROS M.Covariance control for multisensor systems ［J］.Aerospace and Electronic Systems,IEEE Transactions on，2002，38（4）：1138-1157.

［12］王玉生,田康生,朱康,等.基于目标估计协方差控制的传感器资源管理算法［J］.现代防御技术,2003，31（2）：52-54.

［13］HINTZ K J，MCVEY E S.Multi-process constrained estimation ［J］.Systems，Man and Cybernetics，IEEE Transactionson，1991，21（1）：237-244.

［14］周文辉.相控阵雷达及组网跟踪系统资源管理技术研究［D］.长沙：国防科学技术大学，2004.

Sensor Management Algorithm Based on Improved Covariance Control

Lu Peng-fei，PENG Dong-liang，ZUO Yan，GU Yu
（Hangzhou Dianzi University，Hangzhou 310018，China）

To solve the problem of high computational need and frequent switching caused by complete search algorithm in traditional sensor management algorithm based on covariance control，an improved algorithm is proposed in this paper.The algorithm determines whether the sensors used at last time step can meet the accuracy of target tracking at first，by consulting the bias of the filtering covariance matrix and the desired one，using dimensional transformation and eigenvalue calculation.Set a threshold for all eigenvalues of the dimensional uniformity matrix which is transformed from the bias matrix，then determine whether the filtering covariance satisfys expectation or not，and decide whether to maintain the current sensors for choice.The performance of the proposed algorithm is tested in constant velocity（CV），constant acceleration（CA）and coordinate turn（CT）cases.The simulation results demonstrate that the algorithm not only meets target tracking accuracy in most of the tracking scenes，but also can improve the timeliness of sensor management and reduce switch frequency.

sensormanagement，covariancecontrol，targettrackingaccuracy，dimensional transformation

TN953

A

1002-0640（2016）07-0028-06

2015-06-08

2015-07-11
*

国家自然科学基金资助项目（61174024）

吕鹏飞（1991-），男，安徽宣城人，硕士研究生。研究方向：传感器资源管理。