单位圆内高阶齐次线性微分方程解与小函数的关系
2016-08-17吴元平陈莉五邑大学数学与计算科学学院广东江门529020
吴元平,陈莉(五邑大学 数学与计算科学学院,广东 江门 529020)
单位圆内高阶齐次线性微分方程解与小函数的关系
吴元平,陈莉
(五邑大学 数学与计算科学学院,广东 江门 529020)
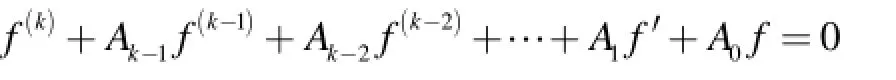
高阶齐次线性微分方程;单位圆;小函数;收敛指数
1 引言与问题
2000年,J.Heittokangas[5]首先在其博士论文中系统地研究了单位圆上的微分方程解的增长性,之后国内学者也开始了相关研究[6-9].
2002年,陈宗煊[3]研究了高阶齐次线性微分方程,得到了如下关于解的增长级的结果:
定理A假设 A0(z) ,… ,Ak-1(z )是Δ内解析函数且满足:1)σ ( Aj)< σ(A0), j= 1,2 … ,k-1;或者2)A0(z)是可允许的, A1( z) ,… ,Ak-1(z )是不可允许的,那么:的每个非零解 f具有无穷级.
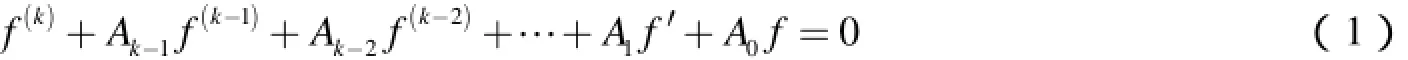
2008年,曹廷彬和仪洪勋[4]进一步研究了方程(1),得到了如下关于解的超级结果:
定理B假设 A0(z) ,… ,Ak-1(z )在Δ内解析,如果那么方程(1)的所有解 f(≠ 0)都满足 σ2(f)= σM(A0)≥ σ(A0).
陈宗煊等[1]首先研究了关于一类二阶微分方程解与小函数的关系,此后关于高阶微分方程解与小函数的关系得到了大量的关注.而单位圆上的高阶微分方程解与小函数关系的研究结果较少,金谨[2]结合定理B,证明了如下结果:
定理C设 A0(z), A1(z ),… ,Ak-1(z )是单位圆Δ内的解析函数,且则方程(1)的不恒为零解析解 f( z)满足
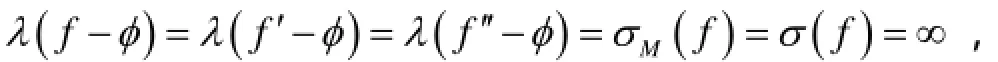
其中, φ( z )是 f( z)的小函数.
自然地,我们考虑在定理A的条件下,如何得到方程的解与小函数的关系,即:
定理 设 A0(z), A1( z) ,… ,Ak-1(z )是单位圆Δ内的解析函数,A0(z)是可允许的,A1( z),…, Ak-1(z )是不允许的,且 max {Aj(z), j = 0,1,…,k-1}=σ<∞,则方程(1)不恒为零解析解 f( z)满足

其中, φ( z )是 f( z)的有穷级小函数.
注:令 k= 2,如果 A1= 0,则得到文献[10]的定理1,故本文定理推广了文献[10]的结果.
2 所需引理
引理1[3]723设 f( z)是单位圆Δ内的亚纯函数,k是自然数,则其中且满足,若 f( z)是有穷级,则
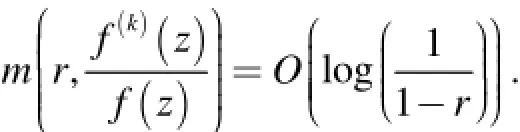
引理2[2]756设不恒为零的 f( z)是微分方程(1)的解, g( z) = f( z)- φ (z),则
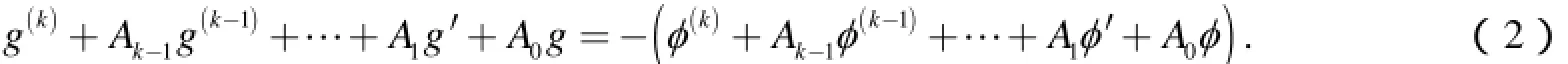
引理3[2]756设不恒为零的 f( z)是微分方程(1)的解, w( z) = f ′(z)- φ (z),则
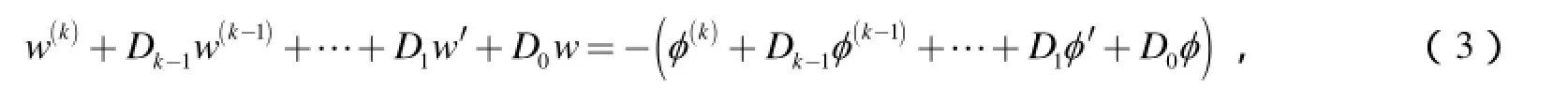
引理4[2]757设不恒为零的 f( z)是微分方程(1)的解, h( z) = f ′(z)- φ (z),则
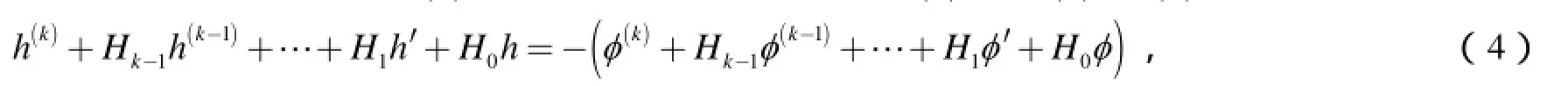

引理5[4]723设 f 是Δ内解析函数 σ ( f )= σ<+∞,那么对任意充分大的 ε > 0,当 r ∈ [ 0,1)且充分接近1时,有
引理6[11]设 f ( z)是单位圆Δ内的亚纯函数,则 σ (f)≤ σ (f)≤ σ (f )+1.M
3 定理的证明
证明 设不恒为零的 f ( z)是微分方程(1)在单位圆Δ内的解析解.由定理A知, σ ( f )=∞;又由引理6知, σM(f )=∞.
令g( z) = f( z)-φ (z),w( z) = f ′ (z)-φ (z),h( z) = f ′ (z)-φ (z),则 f( z) ,f ′(z ) ,f ′ (z )取小函数φ(z )的点分别是 g ( z),w( z),h( z)的零点,且有
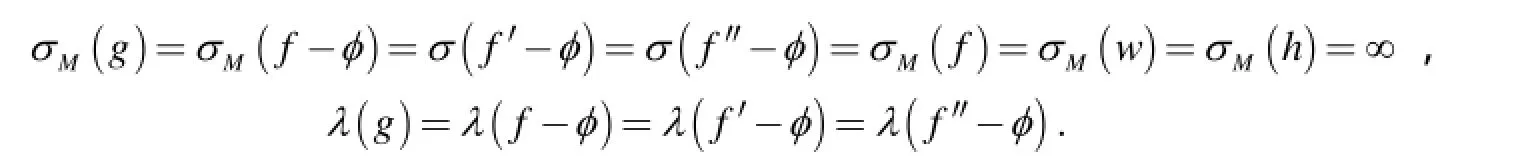
因为 A0(z)是单位圆Δ内的可允许的解析函数, A1( z) ,… ,Ak-1(z )都是单位圆Δ内的不可允许的解析函数,所以
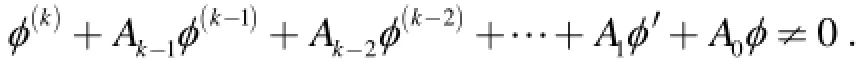
假定有φ(k)+ Ak-1φ(k-1)+ Ak-2φ(k-2)+…+A1φ ′+A0φ=0,则
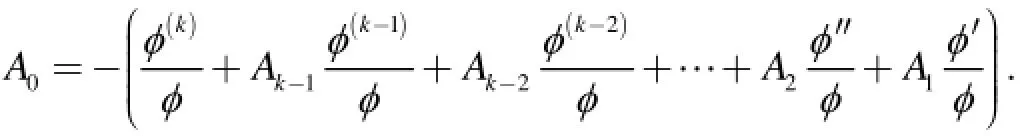
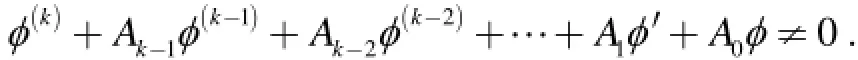

同理,由引理3和引理4可得:
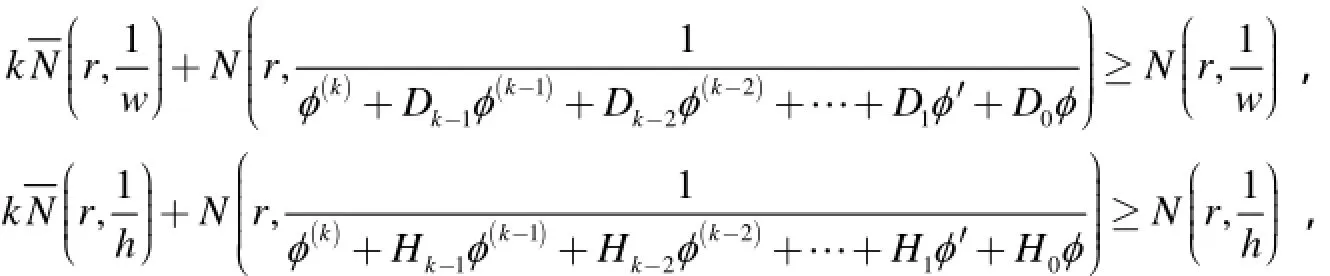
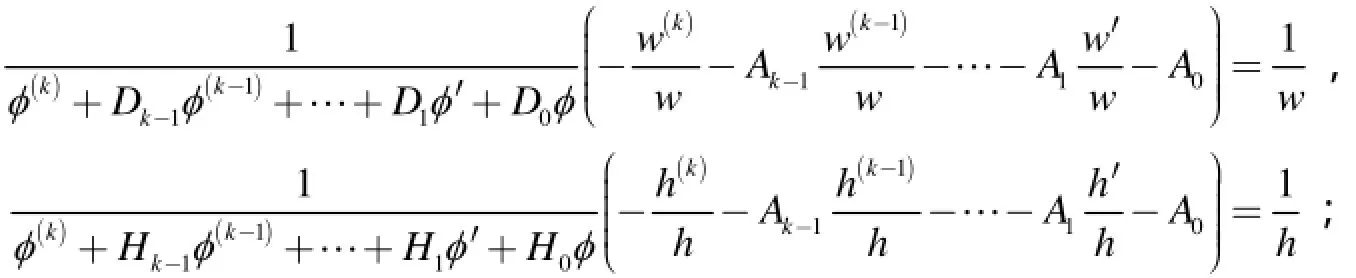
因此:
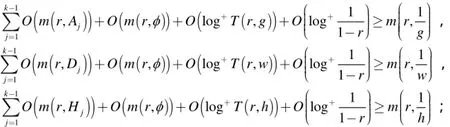
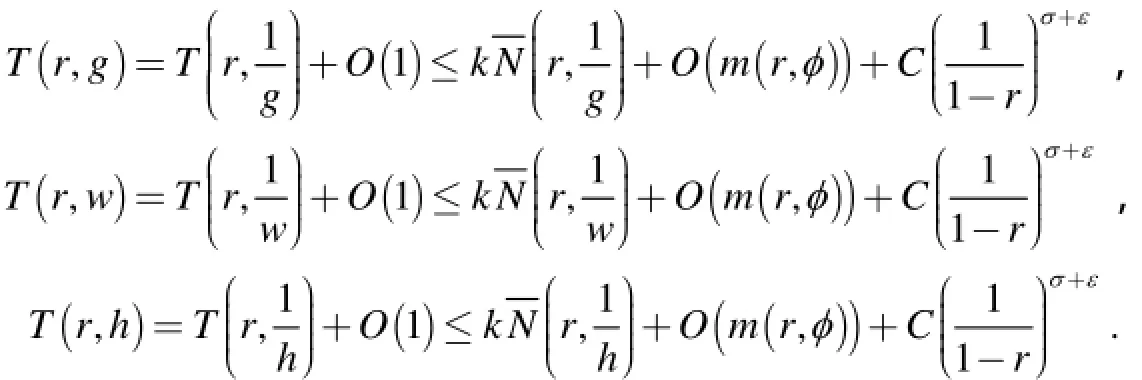
又φ( z )是 f( z)的小函数,因此微分方程(1)的所有不恒为零的解析解 f( z)都满足

[1]陈宗煊,孙光镐.一类二阶微分方程的解与小函数的关系[J].数学年刊,2006,27A(4):431-442.
[2]金谨.单位圆内高阶齐次线性微分方程解与小函数的关系[J].应用数学学报,2014,37(4):754-764.
[3]陈宗煊.一类单位圆内微分方程解的性质[J].江西师范大学(自然科学版),2002,26(3):272-281.
[4]曹廷彬,仪洪勋.关于单位圆内解析系数的二阶线性微分方程解的复振荡[J].数学年刊,2007,28A(5): 719-732.
[5]HEITTOKANGAS J.On complex differential equations in the unit disc[J].Ann Acad Sci Fenn Math Diss,2000, 122:1-54.
[6]XU Junfeng,ZHANG Zhanliang.Growth order of meromophic solutions of higher-order linear differential equations[J].Kyungook Math J,2008,48:123-132.
[7]CAO Tingbin,CHEN Zongxuan,ZHENG Xiumin,et al.On the iterated order of meromorphic solutions of higher order linear differential equations[J].Ann of Diff Equ,2005,21(2):111-122.
[8]CAO Tingbin,YI Hongxuan.The growth of solutions of linear differential equations with coefficients of iterated order in the unit disc[J].Math Anal Appl,2006,319(1):278-294.
[9]李叶舟.单位圆盘上二阶微分方程解的增长性[J].纯粹数学与应用数学,2002,18(4):295-300.
[10]甘会林,孔荫莹.单位圆内二阶线性微分方程的解及其导数的不动点[J].江西师范大学学报(自然科学版),2008,32(6):671-673.
[11]CHEN Zongxuan.The fixed points and hyper order of solutions of second order complex differential equations [J].Acta Math Sci Ser A Chin Ed,2000,20(3):425-432.
[责任编辑:熊玉涛]
Relationship Between Solutions of the Higher Order Homogeneous Differential Equation and the Small Functions in the Unit Disc
WU Yuan-ping,CHEN Li
(School of Mathematics and Computational Science,Wuyi University,Jiangmen 529020,China)
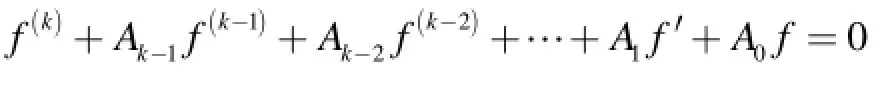
higher order homogeneous differential equation;unit discs;small functions;convergence indexes
O174.5
A
1006-7302(2016)03-0010-04
2016-03-28
吴元平(1989—),男,广东广州人,在读硕士生,主要从事复分析研究.
