湖泊水资源量质耦合态下宏观用水优化
——以太湖流域为例
2016-08-16刘钢,陈兰,王圣
刘 钢,陈 兰,王 圣
(1.河海大学管理科学研究所,江苏 南京 211100; 2.江苏沿海开发与保护协同创新中心,江苏 南京 210098;3.国电环境保护研究院,江苏 南京 210031)
湖泊水资源量质耦合态下宏观用水优化
——以太湖流域为例
刘钢1,2,陈兰1,王圣3
(1.河海大学管理科学研究所,江苏 南京211100; 2.江苏沿海开发与保护协同创新中心,江苏 南京210098;3.国电环境保护研究院,江苏 南京210031)
摘要:针对湖泊水资源配置管理中量质耦合现象,从水资源量质耦合状态分析入手,引入联合分布概率理论,构建基于水质与水量的Copula函数模型,揭示流域水资源“量”与“质”的内在耦合态,并在此基础上,基于IPCC提出未来情境仿真框架,以决策树理论从宏观角度开展太湖流域用水结构优化策略研究,提出逐步关停淘汰企业,建立循环经济实现产业升级的工业用水优化策略;通过采取新型种养殖模式提高农产品价格推动科学生产的方法来实现有机农业的农业用水策略;从低碳生活入手,做到一水多用,逐步改变生活方式的生活用水策略。
关键词:水量水质耦合;Copula函数;决策树;宏观用水策略
随着世界人口的增长和经济的迅速发展,水资源供需矛盾将进一步激化,水资源危机不断加剧。地球表面70%以上被水覆盖,而淡水资源占比为2.52%,其中,易于开发利用的水体仅占淡水总储量的0.34%,不到全球总储量的万分之一。世界上约有80多个国家40%的人口面临缺水问题。水资源总量匮乏已经成为制约人类生存发展的核心瓶颈。
中国是世界上严重缺水的国家之一,总缺水量约530亿m3/a, 人均水资源量呈下降趋势。同时,水资源的时空分布不均,总体呈“南多北少”分布,约有80%分布在长江流域及其以南地区;由于季风气候的强烈影响,我国降水和径流的年内分配很不均匀,夏秋多,冬春少,且年际变化大,少水年和多水年持续出现,旱涝灾害频繁;另一方面,在人类生产生活过程中,用水效率低下、水污染事件频发进一步加剧了水资源稀缺状况[1]。太湖流域是长江三角洲的核心区域,其中江苏省占流域的53%,但是江苏省水生态问题不容乐观,存在严重的水质型与水量型缺水。江苏省年平均本地水资源量320亿m3,人均432 m3,仅为世界人均占有量(12 900 m3)的3.35%,全省近三分之二的水体劣于Ⅲ类水;重点水功能区水质达标率仅为50%左右,同时南水北调工程也对江苏省的水生态系统环境影响巨大。
所以,进行水量水质联合调度,合理利用水资源,缓解地区供水矛盾,提高水资源和水环境的承载能力,改善生态环境,维持社会、经济、生态的可持续发展,已是一个刻不容缓的问题[2]。近年来,虽然国内外的学者对此作了大量的研究,但大多数是将水资源的“质”属性和“量”属性隔离开进行分析,罕见基于耦合状态的实例[3]。笔者从太湖流域水资源量质耦合态分析入手,提出将水质与水量同时考虑的联合分布概率的概念,引入Copula理论,构建了水质水量的联合分布函数,揭示流域水资源的“量”与“质”的内在耦合态,并在此基础上,以水质水量的联合分布概率函数为核心要素,基于《IPCC排放情境特别报告(SRES)》(以下简称IPCC)情境框架,通过决策树模型对宏观状态的工业、农业、生活用水策略结构进行分析,构建基于水量水质耦合态的宏观用水优化策略。
1 太湖流域水资源量质耦合态分析
1.1湖泊水资源量质循环结构分析
流域水资源管理是对流域水资源供给与需求关系的协调过程, 是以追求可利用水资源的最大效益, 实现流域人水和谐、经济系统和生态环境系统和谐发展为最终目标的水资源统一调控和协调管理[4]。实际上,流域水资源的管理及分配是一个复杂的问题,不仅涉及生态环境的保护与利用,更涉及社会、经济、政治等诸多方面的稳定。只有重视水循环过程中的每一个环节, 充分考虑水循环的每一个过程:大气过程、地表过程、土壤过程等的消耗转化,通过探究水量与水质的互动关系,明确水资源量质耦合机理,才可提升流域水资源管理可行性。笔者以太湖流域为例,研究水资源量质循环结构,如图1所示。
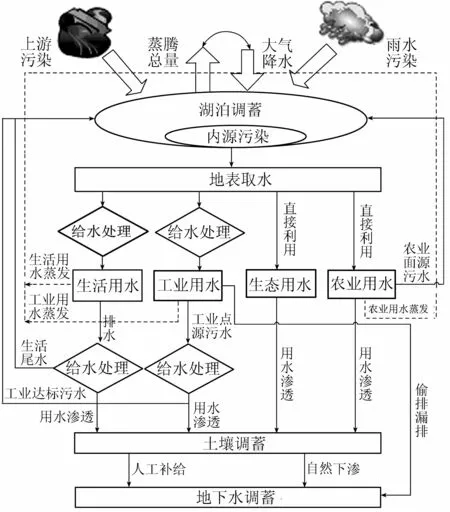
图1 太湖流域水资源量质循环结构
图1所示,湖泊水量主要来源于大气降水以及上游水体,在自身内部循环后,用于农业、工业、生活、生态等以及必要的蒸发和渗透。蒸发的同时也将水中的污染物蒸发到空气中;水渗透进入土壤,一部分用于土壤的调蓄,另一部分进入地下水循环中。在整个水量循环过程中,每一个环节都会伴随着污染物的产生,集中体现在:①在大气降水过程中不可避免地会将空气中的污染物质随着雨水带到湖泊中,如酸雨等雨水污染源。②水流会将湖泊上游的污染物质带到湖泊中,且上游水质很难预测及控制,如上游来水污染源。③在湖泊内循环过程中,随着鱼虾等生物的生存,呼吸、排泄、死亡等生存过程中产生废弃物,虽然湖泊本身也具有分解某些污染物质的能力,但其内源污染也是湖泊重要的污染来源。④水源用于居民的日常生活中时,居民排水主要是厨卫污水,以COD、氨氮、总磷含量高为特点,经城市污水处理厂处理达标后排放,然而城市污染一级A排放标准中大部分污染物质量仍高于地表水质量标准中的Ⅴ类水体要求,即对湖泊而言,生活污水处理后排放仍是污水。⑤农业用水一般较少进行污水综合处理,通过河渠网络直接排入河湖,污水中主要含有牲畜粪便、化肥、农药等污染物质,污染物中COD、氨氮、总磷含量较高。⑥工业生产排放的污水经统一处理达到国家排放标准后外排。然而,伴随着成本考核、监管漏洞、政府纵容等问题,工业企业始终存在着偷排漏排行为,尾水未达标甚至未处理直接排放,污染严重。⑦生态用水主要供自然生态系统生存发展使用,是生态环境可持续发展的保障资源,一般忽略其污染物产生情况。
综上所述,湖泊水资源量质循环过程中不仅包括湖泊调蓄,而且包括地下水调蓄、土壤调蓄等,在水量循环过程中始终伴随水质变化。水量水质产生变化的原因与人类生产生活的方式密切相关,可以归为直接原因和间接原因:直接原因有工业面源污水、农业点源污水、生活尾水的排放,湖泊水使用后将产生的污水排入湖泊中,不仅使水量减少,而且使水质明显下降;间接原因包括上游污染物质、雨水污染以及湖泊本身内部循环产生的污染,上游污染水以及雨水流入湖泊在水量增大的同时也降低了水质,而污染水以及酸雨等雨水的形成很大一部分与人类的行为有关,湖泊水污染程度越严重,人类为净化水所做的工作越多,可用水量越少,影响着人们的生产生活方式。所以,湖泊水污染的产生受到人类生产生活方式的影响,同时,水质水量的关系也影响着人类的生产生活方式。因此,针对湖泊水资源量质循环过程中的耦合关系,有必要从联合分布的视角考虑水量与水质互动关系的耦合状态,从而实现统一管理。
1.2模型构建
针对上述问题,从联合分布的视角考虑水量与水质互动关系的耦合状态问题,近年来,国内外学者取得了较为广泛的研究成果,其中,关于Copula函数研究进展显著[5-8],其在水文多变量分析计算中具有良好的应用前景。因此,笔者将Copula函数应用于太湖流域水资源量质耦合分析过程,通过构建水质水量的联合分布概率函数,明确太湖流域人水互动关系以及水资源量质耦合结构之后,建立相关耦合模型,为太湖流域水质管理、水量配置问题提供可靠的依据。
1.2.1构建湖泊水资源量质耦合态Copula经验公式
Copula函数是定义域在[0,1]均匀分布的水质与水量的联合分布函数,将水质x、水量y的边际分布连接起来构造联合分布:
(1)
式中:C()为Copula函数;F1,F2为水质与水量的边际分布;r为Copula参数。
由Sklar定理[9]可知,令H(*,*)为具有边缘分布F(*)和G(*)的联合分布函数,即有Copula函数C(*,*),满足以下等式:

(2)
其中,若F(*),G(*)连续,则C(*,*)唯一且确定;反之,若F(*),G(*)为一元分布函数,则C(*,*)为相应的Copula函数,那么式(2)中H(*,*)是具有F(*),G(*)边缘分布的联合分布函数。
由以上Copula定义可以采用以下公式计算边缘分布的经验频率。
(3)
式中:P为X≤xm的经验频率;m为xm的序号;N为样本容量。
1.2.2湖泊水资源量质耦合态Copula联合分布函数构建
在水资源计算中,采用最多的是阿基米德Copula函数,根据不同的Copula函数对相关性的适应范围[8],笔者选择通用性较好的Clayton函数来构造联合分布函数。
(4)
式中:xi为水质参数;yi是水量参数;θ为表征水质与水量2个变量之间关系的耦合态系数;i为湖泊水循环中每类污染产生过程对应的第i种情境。
2 实例分析
太湖流域地跨苏、浙、皖、沪三省一市,总面积36 895 km2。历来是我国人口密度最大、工农业生产发达、国民经济产值和人均收入增长幅度最快的地区。据2013年统计资料,太湖流域总人口占全国总人口的4.4%,GDP占全国GDP的 10.2%,人均GDP是全国人均GDP的2.3倍,其中江苏省太湖流域人口占全省总人口的22.6%,太湖流域在江苏省发展大局中的地位举足轻重。
自20世纪90年代以来,江苏省经济化社会发展迅速,污染物排放量不断增加,水环境持续恶化,导致江苏省出现水质型缺水与水量型缺水并存的水生态危机。
2.1数据来源
选择太湖流域2012年6月到2015年5月共计35个月的水量和水质(采用氨氮指标)数据,数据来源于《太湖流域省界水体水资源质量状况通报》与《水情月报》。
2.2分析与讨论
2.2.1参数估计
太湖流域的水量和水质(采用氨氮指标)月总量分布以及概率密度情况,如图2、图3所示。
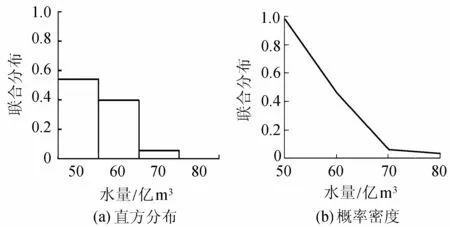
图2 太湖流域月水量直方分布及其概率密度

图3 太湖流域月氨氮总量直方分布及其概率密度
如图2、3所示,各边缘分布的拟合曲线能够反映出边缘分布的频率直方图,因此,可以用此分布以及参数来表示水量与水质的边缘分布,其参数选择是合理的。
2.2.2拟合优度检验
目前,在水文分析计算中,一般假设水文变量服从皮尔逊Ⅲ型分布。把水质和水量分别用x和y来描述,在实测数据中,把(x1,x2,…,xn)和(y1,y2,…,yn)按照系列x的升序排列,挑选排好次序数据中的xi≤xj,yi≤yj(i (5) 对于两变量单参数阿基米德Copula函数的参数估计,常采用Genest等提出的非参数估计方法[11],结合式(4),将太湖的水量和氨氮指数的经验频率和理论联合分布频率值绘于图4中。 图4 水量与水质联合观测点的理论分布和经验分布的比较 如图4所示,F(x,y)为理论联合分布,Femp(x,y)为经验联合分布函数。对其进行拟合优度检验,得到R2=0.989 7, 证明笔者所选取的Copula函数是合理的,可用来分析湖泊水资源量质耦合态问题。 2.3湖泊水资源量质耦合态情境仿真分析 考虑到人类经济社会发展变化情况,引入IPCC中的未来发展情境框架,通过对比分析可知,更为符合现状人类生存环境的社会状况是情境族B2。B2情景族描述了这样一个世界:强调经济、社会和环境可持续发展的局地解决方案。在这个世界中,全球人口数量持续增加,但增长率减缓,经济发展处于中等水平,技术变化速度较快且更加多样化,同时也致力于环境保护和社会公平。总体来看,在B2情境下,排放量减少,环境更稳定,能源更清洁,水环境承载能力以及水环境容量都有显著提升,即水质逐步好转,水量增长放缓。 因此,按照B2情境设计,分别对式(4)中的水量y,水质x进行偏导分析,以分析该情境下水质水量耦合关系的变化。 (6) (7) 如式(6)、式(7)所示,按照B2情境设计,太湖流域水质水量的耦合态系数θ=0.57,通过分析可知:①当水质x不变,水量y增大时,y-θ减小,(x-θ+y-θ-1)减小,函数值增大;同理,水量y不变,水质x增大时,函数值增大。这说明水质与水量对联合分布函数造成同向变化,选择的函数符合预期假设。②当式(6)或式(7)等于0时,x=0(y=0)或者x-θ+y-θ=1,因为水质或水量不可能等于0,当且仅当水质与水量满足x-θ+y-θ=1时,此时水质与水量耦合态达到最佳效果。可以发现,面对B2情境下的经济社会发展,当降低水质污染水平时,变相提高了可用水量,因此,节能减排政策仍然具有显著的效力。 在此基础上,基于太湖流域水质与水量耦合态,以IPCC设定的B2情境为框架,分别对太湖流域工业、农业以及生活中的产污行为进行决策树评估,选择水量与水质耦合态下的水资源管理策略的优化对策。 就我国现行水资源量质标准而言,城市污染一级A排放标准中大部分污染物质量仍高于地表水质量标准中的Ⅴ类水体要求,如我国地表水排放标准为GB18918—2002《城镇污水处理厂污染物排放标准》,该标准适用于中华人民共和国领域内江河、湖泊等具有使用功能的地表水水域,以氨氮指标而言,GB18918—2002给出的一级A标准为5(8) mg/L,然而GB3838—2002《地表水环境质量标准》中Ⅴ类水体氨氮指标为2.0 mg/L,而Ⅴ类水体主要适用于农业用水区及一般景观要求水域,已不适用于人类生产生活。 因此,污水达标排放也已成为不可用水资源。有必要系统思辨人类生产生活与水资源量质耦合关系,从宏观层面辨析更适于生态文明建设理念的人水关系,从而从根源上提高水资源管理水平,促进人类社会的可持续发展。笔者将通过决策树分析模型,系统分析工业、农业、生活三方面用水结构,基于湖泊水资源量质耦合态,从宏观角度提出具有可操作性的工业、农业、生活用水优化策略。笔者主要采用决策树的方法对每个领域的解决方法进行评估,采用数值仿真的方法计算每一个情况出现的可能性以及带来的效益值。 3.1工业用水策略优化数值仿真 人类生产活动造成的水体污染中,工业引起的水体污染最严重,如工业废水,它含污染物多,成分复杂,不仅在水中不易净化,而且处理也比较困难。根据工业污染以及国家经济发展现状,从生态环境以及环保意识2个方面提出解决方法,采用数值仿真方法计算得出每一种方法对应的效益值以及出现的可能性,如表1所示,并进行决策树评估,如图5所示。 表1 工业用水决策树数值仿真 图5 工业用水策略决策树优化模型 如图5所示,根据最新出台的《水污染防治行动计划》(以下简称“水十条”)规定,以取缔“十小”企业,整治“十大”行业为纲领,以保障经济发展,改善城市环境为原则,采取突出重点,分步实施,依次推进,限期淘汰,逾期关闭的方式,首先从污染最严重的企业、最落后的工艺开始,每年淘汰关闭一批,实施环境污染末位淘汰,以此关停淘汰企业,扩大非污染企业,改变城镇企业结构,改善环境,进一步建立循环经济,实现产业升级。关停部分淘汰企业以及污染严重的企业,不仅节约了水量,而且污染物质减少,提高了水质,通过式(5)与式(6)的分析可知,水质提高,水量增大的情况下,水质与水量的耦合关系更符合IPCC中的未来发展情境B2,且相对于其他措施,更具可行性。因此,通过分析工业用水策略决策树的优化模型可以发现:在工业用水过程中,逐步关停淘汰企业,建立循环经济,实现产业升级是一项明智之举。 3.2农业用水策略优化数值仿真 在农业生产过程中,逐渐增加的化肥使用量以及养殖业产生的粪便不仅使营养流失,而且导致水体N、P等物质的不均衡,出现富营养化等现象,污染水源。农业污染是重要的污染源之一,如何使农业生产过程中产生的污染物达到最少,对水体的污染程度减小,是刻不容缓的问题。笔者从有机农业、环保观念以及生态治理3个方面进行决策树优化策略的选择,采用数值仿真方法计算得出每一种方法对应的效益值以及出现的可能性,如表2所示,并进行决策树评估,如图6所示。 如图6所示,根据周泽江[12]提出的健康原则、生态原则、公平原则和关爱原则四大原则,从控制农 表2 农业用水决策树数值仿真 业污染源出发,合理灌溉,科学使用农药,减少农药残留物流向湖泊,平衡使用农家肥与化肥,控制减少含有氮磷化肥的总量,并且通过检测土壤各元素浓度鉴别农产品是否合格,提高合格农产品的价格,推动科学的生产过程。更重要的是采取新型种养殖模式(种植—养猪—沼气),用种植业带动养殖业,养殖业推动沼气工程的进行,打破传统的农业模式,使物质得到重复利用,减少污染,实现物质与能量的转化,全面减少污染物。众所周知,今天的生态农业,不是光讲安全农业,十八大提出了生态文明,并写进党章,所以有机农业是一个必然的趋势,而且在节约水量的同时提高了水质。通过分析农业用水策略决策树的优化模型可以发现:采取新型种养殖模式、提高农产品价格推动科学生产的方法来实现有机农业,更符合水质与水量耦合关系的要求,同时也很好地适应了现代社会的需求。 3.3生活用水策略优化数值仿真 图6 农业用水策略决策树优化模型 生活用水对水体的污染是由城市生活污水、垃圾和废气造成的,集中的城市人口加剧了城市的污染,同时造成了污染物处理的不便。城市污染源对水体的污染主要是生活污水,它是人们日常生活中产生的各种污水的混合液,其中包括厨房、洗涤房、浴室和厕所排出的污水。笔者从人类自身生活方式的转变以及环保意识出发,采用数值仿真方法计算得出每一种方法对应的效益值以及出现的可能性,如表3所示,并进行决策树评估,如图7所示。 表3 生活用水决策树数值仿真 图7 生活用水策略决策树优化模型 如图7所示,相对于完全依靠人们的环保观念以及政府罚款,做到低碳生活显得更为高效,日常生活中要强调节水减污,把再生水以及水的重复利用提高到较高位置,引导居民节约利用水资源,做到低碳生活,一水多用,节约用水,加强垃圾回收,对于污水排放前进行一定程度的过滤、吸附等简单操作,减少油性物质等的排放。通过分析生活用水策略决策树的优化模型可以发现:低碳生活的方式不仅可操作性强,有利于培养环保意识,更重要的是可以做到持续的节约水资源,减小污水处理的压力,做到了水量增加,水质提高,所以低碳生活的生活方式更符合水质与水量的耦合态以及人类生存发展的要求。 随着经济发展和人口增加, 水污染引发了一系列生态环境问题,但在经济社会进程中,水资源发挥着不可忽视的作用,涉及经济、社会和环境等众多问题。笔者围绕湖泊水环境容量小、水资源承载能力差的问题,以太湖流域为例,叙述了湖泊水循环过程中水质与水量的耦合态问题,引入联合分布概率理论,建立了水质与水量双维度的Copula函数,通过算例分析表明,笔者构建的模型具有实用性和高效性。最后在IPCC情境B2的框架下,运用决策树分析方法分别对工业、农业、生活用水等行为提出水资源管理策略优化方案。 参考文献: [ 1 ] 郑通汉.中国水危机:制度分析与对策 [M].北京: 中国水利水电出版社,2006. [ 2 ] 王亚华.水权解释 [M].上海: 上海人民出版社,2005. [ 3 ] 王宗志,张玲玲,王银堂,等.基于初始二维水权的流域水资源调控框架初析 [J].水科学进展,2012,23(7): 590-598. [ 4 ] 王浩,杨贵羽.二元水循环条件下水资源管理理念的初步探索 [J].Chinese Journal of Nature,2010,32(3): 129-133. [ 5 ] 熊立华,郭生练.Copula联结函数在多变量水文频率分析中的应用 [J].武汉大学学报(工学版),2005,38(6):16-19. [ 6 ] 莫淑红,沈冰.基于Copula函数的河川径流丰枯遭遇分析[J].农林科技大学学报(自然科学版),2009,37(6): 131-136. [ 7 ] 许月萍,李佳.Copula在水文极限事件分析中的应用[J].浙江大学学报(工学版),2008,42(7): 1119-1122. [ 8 ] 张翔.基于Copula函数的水量水质联合分布函数[J].水力学报,2011,42(4): 483-489. [ 9 ] SKLAR A.Fonctions de repartition an dimension et leurs marges[J].Publication de I’Institut de Statistique de I’Universite de Paris,1959,8:229-231. [10] ZHANG L.Multivariate hydrological frequency analysis and risk mapping[D].Louisiana State: Louisiana State University,2005. [11] 钟波,张鹏.Copula函数选择方法[J].重庆工学院学报(自然科学版),2009,23(5):155-160. [12] 周泽江.发展有机农业与有机食品不仅仅是为了健康[J].新农村,2015(10):41-43. 基金项目:国家社会科学基金青年项目(14CGL030);教育部高等学校博士学科点专项科研基金(新教师类)(20130094120022);河海大学中央高校基本科研业务费项目(2013B04714) 作者简介:刘钢(1981—),男,山西太原人,讲师,博士,主要从事生态经济学研究。E-mail: lglhm@msn.com DOI:10.3880/j.issn.1003-9511.2016.04.013 中图分类号:TV213.3 文献标识码:A 文章编号:1003-9511(2016)04-0051-06 (收稿日期:2015-11-15编辑:方宇彤)

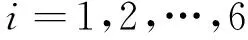
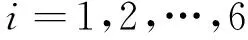
3 湖泊水资源量质耦合态的宏观用水策略优化

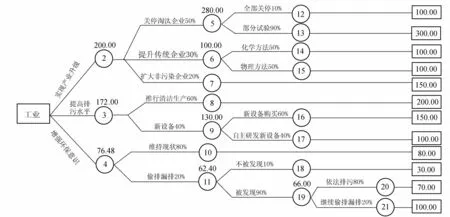
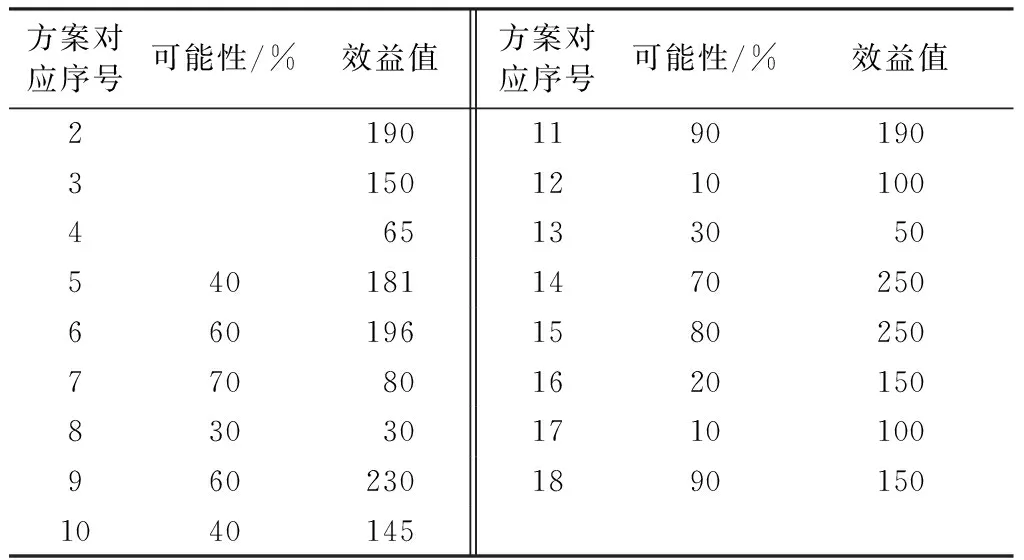
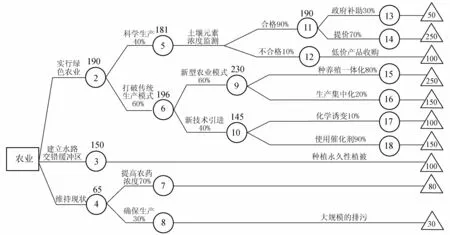


4 结 语
