基于改进机器学习算法的微电网短期负荷预测

齐庭庭， 李建奇

基于改进机器学习算法的微电网短期负荷预测

齐庭庭， 李建奇

（湖南文理学院 电气与信息工程学院， 湖南 常德， 415000）

为了对具有基数小、波动大及随机性强等特点的微电网负荷进行准确预测， 提出了一种基于改进的机器学习算法。该算法包括基于蚁群算法的模型参数寻优和基于改进核函数极限学习机的预测模型2部分。首先， 对蚁群算法信息素的作用方式进行了改进， 并将训练误差用于计算蚁群个体的新增信息素， 从而得到最优的模型参数。其次， 采用基于加权离散距离的方法对训练数据进行筛选， 留下相似度高的训练样本对核函数输出权重进行训练， 从而减少计算量， 提高预测精度。用某小区高层楼宇的电网历史负荷数据， 在 Matlab中对算法进行仿真验证， 结果表明预测算法能较好地实现微电网的负荷预测。

微电网； 负荷预测； 机器学习算法

本文提出了一种基于蚁群算法参数寻优的改进核函数极限学习机的负荷预测方法。对用于解决离散问题的蚁群算法进行了机理改进， 使蚁群算法适用于连续解的寻优， 从而实现对核函数极限学习机的模型参数进行优化。并采用基于加权离散距离的方法对在线训练样本数据库进行筛选， 用加权离散距离较小的一批训练数据， 对参数优化后的核函数极限学习机的在线预测模型输出权重进行训练， 从而减少训练数据冗余度， 提高计算速度和预测结果精度。

1　核函数极限学习机

在神经网络算法快速发展的时候， Huang等［8］在2006年提出一种新的机器学习理论——极限学习机理论。目前， 基于该理论已衍生出基本极限学习机（Extreme Learning Machine， ELM）、在线序贯极限学习机与核函数极限学习机（Extreme Learning Machine with Kernel， KELM）等相关算法［9］。KELM是一种单层前馈神经网络算法， 由于加入了核机制， 因此， 其解决回归预测问题的能力比基本 ELM 算法更强。KELM与支持向量机（SVM）算法相比， 由于KELM算法的输入层权重固定， 且只需要对输出权重进行训练， 因此， 在获得更好或相似的预测精度时， KELM的计算速度更快［10］。

图1　极限学习机算法的神经网络结构

基本ELM算法是一种随机隐藏层的前馈神经网络算法， 其网络结构如图1所示。其表示的前馈神经网络函数表达式为

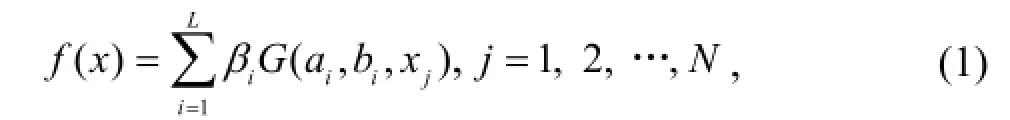
式中： ai为连接输入层与隐藏层节点的输入权重， bi为隐藏层节点的阈值， 且ai， bi随机生成； G（ai， bi， xj）为隐藏层的激励函数；βi为连接隐藏层和输出层的输出权重； N为输入层输入数据xj的维数。结合图1与式（1）可知， 通过隐藏层激励函数可将输入数据从N维空间映射到L维空间。

与BP神经网络等传统回归预测算法相比， ELM算法不仅趋向于获得最小的预测误差， 同时还趋向于最小化输出权重β，即。式中， H为ELM算法的隐藏层矩阵， 且H。输出权重向量β和目标值O的表达式分别为

基本ELM算法通常用于已知激励函数hi（x）的情况， 当激励函数hi（x）未知时， 可对ELM算法使用Mercer条件， 从而构成KELM算法。对于KELM算法， 其神经网络特性方程与基本ELM相同， 但通过引入核函数能获得更好的回归预测精度。ELM_K网络特性方程表述为， 式中： C为待优化参数；ELMΩ为所选核函数， 一般选择高斯核函数， 即， 其中γ为待优化参数。引入高斯核函数后， 隐藏层矩阵由N × L维转化为N × N维。通过采用核函数， 由激励函数构成的隐藏层矩阵H无需知道待求解问题所对应的G（ai， bi， xj）函数。

2　基于蚁群优化算法的离线参数寻优

为了得到最优化的核函数参数 C和 γ， 本文训练相对预测误差最小， 采用改进的蚁群算法进行寻优。20世纪90年代， 意大利学者M. Dorigo和V. Maniezzo等根据蚁群觅食的原理提出了一种新型的智能优化算法——蚂蚁系统（Ant System， AS）。该算法一经提出便得到了飞速的发展， 并形成了蚁群优化算法（Ant Colony Optimization， ACO）， 对解决组合优化、函数优化、系统辨识、数据挖掘等领域的问题有很好的效果。

原始的蚁群算法用于解决离散问题， 蚂蚁的信息素体现在离散点之间的路径上。本文对蚁群算法中种群个体的信息素作用机制进行一定的改进， 将信息素依附在种群个体上， 信息素的作用体现为对其他种群个体的吸引力。种群中的个体总是被信息素吸引力最强的个体吸引。

2.1寻优目标及蚁群构建

用参数寻优目标函数

使所有训练样本的平均预测误差最小。式（2）中： Xi为输入训练样本； yi为训练样本的目标值；iy︵为预测输出值； N为训练样本数。

平均预测误差的取值范围为［0， 1］， 因此， 可将预测误差作为种群个体的信息素产生函数， 其表达式为

信息素更新策略表达式为

式（4）中， η为信息素挥发系数， 取值范围为［0， 1］。

所有种群完成一次搜索之后， 需要根据相应的规则向吸引力最大的个体靠近。本文为了保证种群的多样性和算法的收敛能力， 将种群分为 3部分： （1） 挑选出一定比例信息素吸引力较小的个体， 进行随机大步长移动； （2） 剩下除最大信息素个体外的所有个体向最大信息素个体靠拢； （3） 最大信息素个体在小范围内进行小步长探测， 实现局部精细搜索。

2.2基于蚁群算法的参数寻优步骤

采用蚁群算法进行参数寻优的详细步骤： ① 收集历史数据， 建立训练样本数据集和测试样本数据集； ② 初始化种群数量、迭代次数、收敛条件、种群位置、信息素、信息素挥发系数等相关参数； ③ 用每个种群的参数构建KELM算法模型， 并用训练样本进行训练， 根据式（2）计算每个种群的平均预测误差， 判断是否达到收敛条件， 如果达到收敛条件则结束寻优过程， 否则继续； ④ 根据式（3）计算种群个体的信息素， 根据信息素浓度找出最优个体的位置； ⑤ 取少部分信息素较小的个体做随机位置搜索，剩下除最优位置个体外的其他个体向最优个体移动， 最优个体则按小步长进行局部精细化搜索； ⑥ 按照式（4）更新每个个体的信息素浓度； ⑦ 判断是否达到最大迭代次数， 如果达到则结束寻优， 否则继续；⑧ 通过寻优得到最优参数后， 将其用于构建KELM预测模型。

3　基于加权离散距离的在线训练样本筛选

由于微电网负荷特征整体上随时间变化具有周期性， 因此， 本文选择短时间序列样本作为超短负荷预测在线训练数据库。

设当前时刻为 ti， 当前时刻的输入序列为。已知输入样本序列后， 采用加权离散距离进行在线训练样本筛选， 步骤为： ① 根据当前输入序列， 从训练样本数据库总集中选择所有同期对应时刻的前序短时间序列样本， 形成备用样本集； ② 根据式计算加权离散距离， 式中， wk为前序短时间序列第k个分量的权重，为ti时刻前序短时间序列的第k个分量，为挑选出来备用样本集中的对应ti时刻前序短时间序列的第k个分量， c为前序短时间序列的加权离散距离值； ③对根据第②步计算得到的加权离散距离值进行升序排序， 用选出离散距离较小的前L%个序列对核函数极限学习机进行输出权值训练； ④ 用加权离散距离计算得到的输出权重构建核函数极限学习机。

4　算例

选用高层小区楼宇负荷数据对本文提出的预测算法进行测试。首先， 获取连续23 d间隔为15 min的历史负荷数据， 并对数据进行纠错处理。历史数据每天的采样点数为 96， 因此， 以 96为周期， 从前20 d的历史负荷数据中提取出对应的时间样本集T， 则

从前20 d的历史负荷数据中以滑动时间窗长度为5， 提取出与T对应的前序短时间序列样本集X，

从前20 d的历史负荷数据中提取出与T对应的目标时刻值Y， 且。从第1 d到第19 d， 每天最后1个点为下1 d的第1个点， 如第1 d的最后1个点为第2 d的第1个点的负荷值2， 1y， 第20 d的最后一个时刻取值为前19 d对应时刻的平均值。

设置蚁群算法的种群数为50， 最大迭代次数为300。用第21 d到第23 d的数据进行测试， 测试结果如图2所示， 预测误差如图3所示。

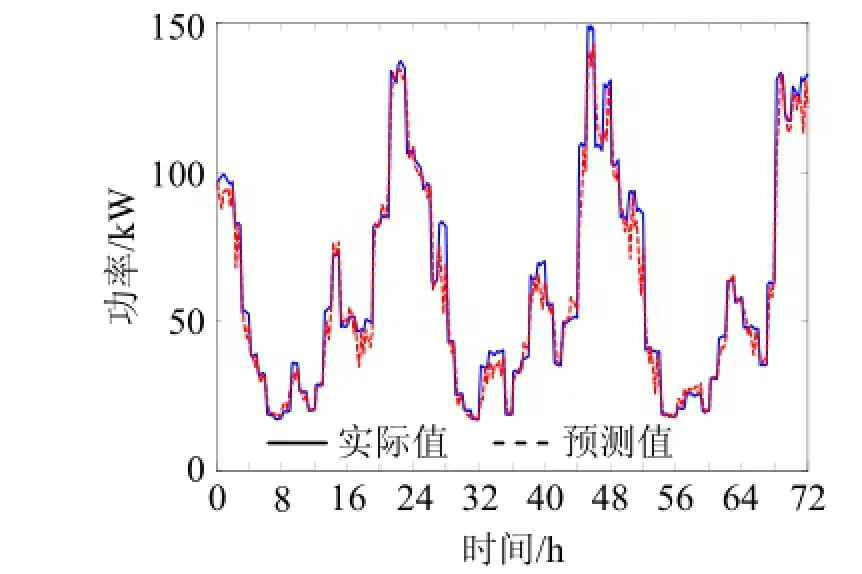
图2　负荷预测结果与实际结果对比

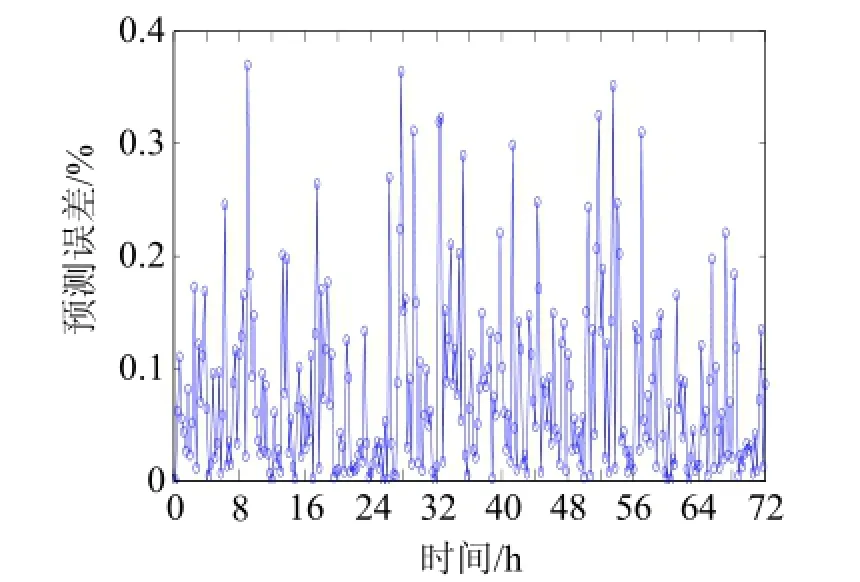
图3　负荷预测误差

从图2中原始负荷曲线可看出， 小区负荷的波动性和随机性很大， 最大负荷约为最小负荷的6倍。但是， 每天都有相似的规律， 上午负荷最小， 下午负荷有所增加， 到晚上负荷达到高峰。图2中的虚线为预测算法获得的预测结果， 整体上看， 预测算法通过学习之后， 能够很好地跟踪实际负荷的变化。

由图 3可知， 大部分时刻的负荷预测误差在 15%以下， 最小预测误差接近 0， 最大预测误差约为38%， 连续3 d的平均预测误差约为7.6%。仔细分析图3可知， 误差较大的情况都发生在负荷由较大值向较小值变化的时候。这是因为用电负荷的突然变化导致算法不能及时准确跟踪突变点， 并且由相对误差的计算公式可知， 此时误差计算的分母（实际负荷）由一个较大值变化为一个较小值， 从而导致了大误差的产生。

5　结论

本文提出了一种基于蚁群算法参数寻优的改进核函数极限学习机的负荷预测方法。对用于解决离散问题的蚁群算法进行了机理改进， 使蚁群算法适用于连续解的寻优， 从而实现对核函数极限学习机的模型参数进行优化。并采用基于加权离散距离的方法对在线训练样本数据库进行了筛选， 从而减少训练数据冗余度， 提高计算速度和预测结果精度。通过仿真实验结果可知， 本文提出的负荷预测算法在微电网负荷预测的应用中能取得较好的效果。

［1］ 董爽. 电力系统短期负荷预测方法综述［J］. 黑龙江科技信息， 2009（29）： 81.

［2］ 张涛. 电力系统短期负荷预测技术的研究与应用［D］. 杭州： 浙江大学， 2007.

［3］ 陆宁， 武本令， 刘颖. 基于自适应粒子群优化的 SVM 模型在负荷预测中的应用［J］. 电力系统保护与控制， 2011， 38（15）： 43-46.

［4］ 师彪， 李郁侠， 于新化， 等. 基于改进粒子群—模糊神经网络的短期电力负荷预测［J］. 系统工程理论与实践， 2010， 30（1）： 157-165.

［5］ 刘梦良， 刘晓华， 高荣. 基于相似日小波支持向量机的短期电力负荷预测［J］. 电工技术学报， 2006， 21（11）： 59-64.

［6］ 张素香， 赵丙镇， 王风雨， 等. 海量数据下的电力负荷短期预测［J］. 中国电机工程学报， 2015， 35（1）： 37-42.

［7］ 汤庆峰， 刘念， 张建华， 等. 基于 EMD-KELM-EKF与参数优选的用户侧微电网短期负荷预测方法［J］. 电网技术，2014， 38（10）： 2 691-2 699.

［8］ 张清鑫. 分布式光伏接入的用户侧微电网功率预测方法［D］. 北京： 华北电力大学， 2014.

［9］ Huang G B， Wang D H， Lan Y. Extreme learning machines： a survey ［J］. International Journal of Machine Learning and Cybernetics， 2011（2）： 107-122.

［10］ Huang G B， Zhou H， Ding X， et al. Extreme learning machine for regression and multiclass classification ［J］. IEEE Trans Syst Man Cybern B Cybern， 2012， 42（2）： 513-529.

（责任编校： 江河）

Short-term load forecasting for microgrids based on improved machine learning algorithm

Qi Tingting， Li Jianqi
（College of Electrical and Information Engineering， Hunan University of Arts and Science， Changde 415000， China）

In order to improve the accuracy of short-term load forecasting， an improved machine learning algorithm is proposed. It consists of model parameters optimization based on ACO （Ant Colony optimization） and forecasting model based on improved KELM （Extreme Learning Machine）. Firstly， the way that pheromone works is modified and the training error is introduced into calculating new pheromone. By this way， the optimal parameters of KELM can be obtained. Secondly， the weighted discrete distance is utilized to screen the training data. The more similar ones will be picked out to train the output weight of KELM. It can reduce calculation and improve the accuracy. The historic load data of a residential building is utilized to conduct the verifying simulations in Matlab. The results show that the proposed algorithm has a good performance in short-term load forecasting for microgrids.

microgrids； load forecasting； machine learning algorithm

TM 715

1672-6146（2016）03-0057-05

10.3969/j.issn.1672-6146.2016.03.012

齐庭庭， 240795741@qq.com。

2016-05-20

国家自然科学基金（61403136）。短期电力负荷预测方法。文献［6］针对海量的负荷数据， 提出了一种基于局部加权线性回归模型和云计算平台的负荷预测模型， 在大数据负荷预测计算效率和精度上取得了较好的效果。由于微电网中用电负荷容量小， 随机性和波动性强， 并且微电网设备计算能力较弱， 因此， 对微电网的负荷预测难度更大。文献［7］提出了一种基于经验模态分解、扩展卡尔曼滤波及核函数极限学习机的组合负荷预测模型， 并采用粒子群对参数进行了优化。该方法虽然能取得一定的预测精度， 但其算法复杂， 实现难度大， 不适合在微电网中推广。

根据目前国内外的相关研究， 按时间尺度可以将电力系统负荷预测分为长期、中期、短期和超短期负荷预测4类［1］。其中， 短期负荷预测与超短期负荷预测主要对未来一天、小时级及分钟级的负荷做出预测， 为电力系统的运行和经济调度提供依据， 是市场环境下编排调度计划、供电计划和交易计划的基础［2］。长期以来， 国内外专家学者对电力系统短期及超短期负荷预测技术进行了大量的研究， 提出了多种有效的负荷预测方法。文献［3-6］研究了大电网的电力负荷预测方法。文献［3］提出了一种基于支持向量机的短期负荷预测模型， 该模型采用粒子群优化算法对支持向量机的参数进行了最优化处理。文献［4］利用改进的粒子群算法对模糊神经网络进行参数优化， 然后建立了考虑气象、天气和日期类型等多个影响因素的短期负荷预测模型。文献［5］将小波分析与支持向量机相结合， 提出了一种小波支持向量机的