液压型风力发电机组的转速和转矩解耦控制

张　寅　孔祥东　陈立娟　艾　超　李　昊

1.燕山大学，秦皇岛，066004　　2.秦皇岛职业技术学院，秦皇岛，066100



液压型风力发电机组的转速和转矩解耦控制

张寅1,2孔祥东1陈立娟1艾超1李昊1

1.燕山大学，秦皇岛，0660042.秦皇岛职业技术学院，秦皇岛，066100

以液压型风力发电机组为研究对象，输出高质量电能为研究目标，针对机组存在的转速和转矩解耦问题展开研究。建立定量泵-变量马达液压传动系统数学模型。从液压传动系统出发，探究影响机组电能输出质量的关键因素，分析该多输入-多输出系统存在的耦合问题，并采用前馈解耦补偿控制方法解耦。分析变量马达和比例节流阀对液压系统输出转速与转矩的控制规律，得到基于高电能质量控制的转速和转矩解耦控制器。以30 kVA液压型风力发电机组半物理仿真实验台为基础，针对提出的控制方法展开研究。仿真和实验结果表明：液压型风力发电机组输出的转速和转矩实现了解耦控制，有效地实现了液压传动系统的稳速控制和传输功率波动的平滑控制。研究结果为液压型风力发电机组高质量电能输出控制和电网友好性能提高奠定了基础。

风力发电；液压传动；稳速控制；功率平滑；解耦控制

0　引言

风能作为一种绿色再生能源，凭借其环境友好和可持久利用的特点[1]，逐渐受到人们的重视。传统风电机组主要以齿轮箱传动和直驱传动两种机型为主，这两种机型存在装机质量大和成本高等不足。液压型风力发电机组作为一种新型机组，采用柔性传动弥补传统机型的不足，并可提高电能质量[2]。

随着风电机组总装机容量逐渐增大，风电机组所带来的电能质量问题也逐渐得到人们的重视[3-5]。风资源的不确定性和风电机组本身的运行特性使风电机组的输出功率是波动的，可能影响电网的电能质量，如电压偏差、电压波动和闪变、谐波等[6]。

针对风力发电机组的电能质量控制问题，国内外学者展开了一系列研究。文献[7]在直驱式风力发电机组原有模型的基础上，提出了一种采用交叉耦合控制抑制低次谐波电流分量的网侧变换器控制策略，对并网谐波电流进行精确控制，改善了系统输出的电能质量。文献[8]以永磁直驱式风力发电机组为研究对象，提出了一种基于模糊算法的储能系统优化控制策略，有效地平抑了风电机组的功率波动。文献[9-11]采用储能方式来实现风力发电机组的有功功率波动平滑。文献[12-13]通过控制发电机转速，使发电机有功功率能够较好地跟踪给定的功率曲线。

上述关于高电能质量控制的研究主要是针对传统机型，但液压型风力发电机组能量传输和功率控制过程与传统的双馈机型和直驱机型相比更为复杂，发电质量问题亟待解决，目前已经成为阻碍该机型走向工程实际的瓶颈。本文针对电能质量问题中的电压波动和闪变问题，从液压型风力发电机组自身特点出发，分析变量马达和比例节流阀对液压系统输出转速与转矩的控制规律，针对机组输出的转速和转矩进行解耦控制，提出了一种液压型风力发电机组输出转速和转矩解耦控制策略，进而实现机组输出功率平滑。

1　液压型风力发电机组原理

液压型风力发电机组[14]的原理如图1所示，液压型风力发电机组主要由风力机、定量泵-变量马达闭式液压传动系统、补油系统和励磁同步发电机组成。定量泵与风力机刚性相连，主要完成风能向液压能的转换，变量马达与同步发电机刚性相连，主要完成液压能向电能的转换，最终变量马达驱动同步发电机旋转，实现机组并网发电。

图1　液压型风力发电机组原理图

2　风力发电机组数学模型

2.1定量泵数学模型

定量泵在风力机作用下输出高压油，其流量连续性方程为

qVp=Vpωp-Ctpph1

(1)

式中，qVp为定量泵的流量；Vp为定量泵的排量；ωp为定量泵的转速；Ctp为定量泵的泄漏系数；ph1为定量泵进出口的压力差。

定量泵负载力矩Tp为

Tp=Vpph1/ηpm

(2)

式中，ηpm为定量泵机械效率。

考虑到定量泵输出端刚度很大，即Gp=0，故定量泵的力矩平衡方程为

(3)

式中，Tr为风力机输出转矩；Jp为定量泵转动惯量；Bp为定量泵的阻尼系数。

考虑效率时，定量泵机械功率输入和液压功率输出的能量平衡方程为

TpωpηpmηpV=ph1qVp=ph1VpωpηpV

(4)

式中，ηpV为定量泵容积效率。

由式(2)和式(3)可得定量泵的状态方程：

(5)

2.2比例节流阀数学模型

比例节流阀在定量泵与变量马达之间起节流调速作用，其阀芯位移方程为

Xv=KUE

(6)

式中，Xv为比例节流阀开口大小；K为比例系数；UE为电压信号。

比例节流阀流量方程为

(7)

式中，Cd为节流口的流量系数；W为节流口的面积梯度；ph2为比例节流阀出口压力；pL为比例节流阀前后压力差；ρ为液压油密度；Kq为流量系数。

2.3变量马达数学模型

变量马达排量控制方程为

Vm=Kmγ

(8)

式中，Vm为变量马达排量；Km为变量马达排量梯度；γ为变量马达摆角大小。

变量马达流量方程为

qVm=Kmγωm+Ctmph2

(9)

式中，ωm为变量马达转速；Ctm为变量马达泄漏系数。

变量马达输出转矩Tm为

Tm=Vmph2ηmm

(10)

式中，ηmm为变量马达的机械效率。

考虑到变量马达输出端刚度很大，即Gm=0，变量马达力矩平衡方程为

(11)

式中，Te为作用在变量马达的电磁力矩；Jm为变量马达的转动惯量；Bm为变量马达的阻尼系数。

变量马达液压功率输入和机械功率输出的能量平衡方程为

ph2qVm=ph2VmωmηmV=TmωmηmmηmV

(12)

式中，ηmV为变量马达的容积效率。

由式(12)和式(13)可得变量马达的状态方程：

(13)

2.4液压管路数学模型

定量泵到比例节流阀间高压管路流量方程为

(14)

式中，V01为定量泵到比例节流阀间的高压管路总体积；βe为油液体积弹性模量。

由式(1)、式(7)和式(14)可得该段管路的状态方程：

(15)

比例节流阀到变量马达间高压管路流量方程为

(16)

式中，V02为比例节流阀到变量马达间的高压管路总体积。

由式(7)、式(9)和式(16)可得该段管路的状态方程：

(17)

2.5液压传动系统状态空间模型

为了分析方便，需要在以下假设条件下建立定量泵-变量马达液压调速系统的状态方程。

(1)定量泵和变量马达之间的连接管道很短，管道中压力损失、流体质量效应和管道动态效应可忽略不计；

(2)定量泵和变量马达的泄漏为层流，其壳体回油压力均为大气压，忽略低压腔壳体的外泄漏量；

(3)高低压管路完全相同，每个腔室内油液密度和体积弹性模量均为常数，且压力均匀相等；

(4)忽略补油系统；

(5)管道中不产生压力冲击，其压力不超过安全阀压力，比例节流阀输入信号较小，不出现压力饱和现象。

定量泵-变量马达液压调速系统的状态方程表达式为

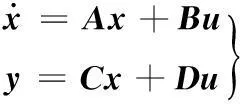
(18)

通过上述分析选取，比例节流阀开口度和变量马达摆角作为输入，以液压主传动系统输出转矩和转速为输出，最终来实现电能质量的优化控制。

系统输入为

(19)

选取系统状态为

(20)

系统输出为

(21)

其中，系统状态方程的各参数分别为

式中，ph20为比例节流阀出口压力基准值；γ0为变量马达摆角基准值；ωm0为变量马达转速基准值。

3　理论分析

3.1耦合分析

由上述状态空间表达式，可得该系统传递函数矩阵：

(22)

由式(19)～式(22)可得系统输入输出控制模型为

(23)

由式(23)可得液压传输系统输入与输出耦合关系，如图2所示。

图2　液压传输系统转矩与转速耦合框图

故上述系统为典型的双输入双输出耦合系统，为实现液压系统输出转速和转矩的高精度高响应动态控制，减少耦合对系统控制的影响，需对上述控制系统进行解耦，使液压系统输出转速和转矩分别更好地跟踪自己的控制输入。

3.2液压传输系统转矩与转速解耦算法

本文采用前馈补偿解耦控制方法，其原理是把某回路的调节器输出对其他回路的影响视为扰动作用，并对此采用前馈控制的方法来解除控制回路之间的耦合。前馈补偿解耦控制框图如图3所示。

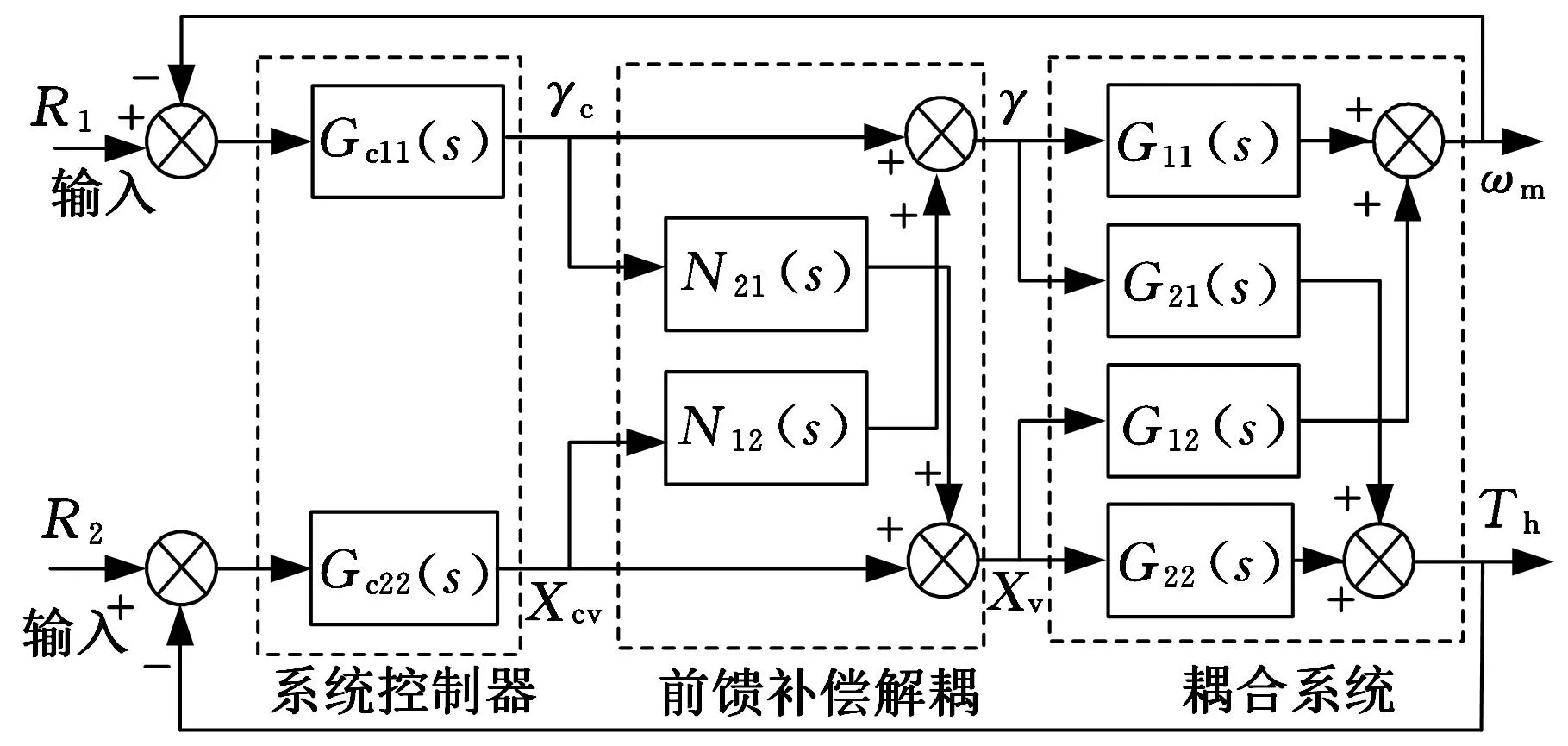
图3　前馈补偿解耦控制框图

由前馈控制原理可得解耦控制器为

(24)

其中，前馈补偿解耦控制器的传递函数N21(s)和N12(s)分别为

经前馈补偿解耦控制器作用，系统传递函数矩阵为

(25)

3.3转速和转矩解耦控制器

3.3.1变量马达摆角控制器

通过控制变量马达摆角调整液压系统输出转速，保证机组并网运行。

由式(17)可得，变量马达摆角控制器为

(26)

3.3.2比例节流阀开度控制器

通过控制比例节流阀开度调整液压系统输出转矩，进而实现液压系统输出功率的快速调整(此时发电机保持并网状态，转速为定值)。在整个液压系统中，节流阀是储能元件，把比例节流阀等效为惯性环节。尽管系统的输入发生突变，通过节流的作用相应量缓变，故可从储能的角度对控制器进行规划。

由定量泵输入的功率，一部分存储到节流阀中，另一部分进入变量马达。故比例节流阀开度控制器为

(27)

4　转速和转矩解耦控制仿真与实验

4.1转速和转矩解耦控制仿真和实验

依据液压型风力发电机组高电能质量控制原理，搭建了30kVA液压型风力发电机组半物理仿真实验平台，基于该实验平台建立了液压型机组高电能质量控制仿真模型，如图4所示。

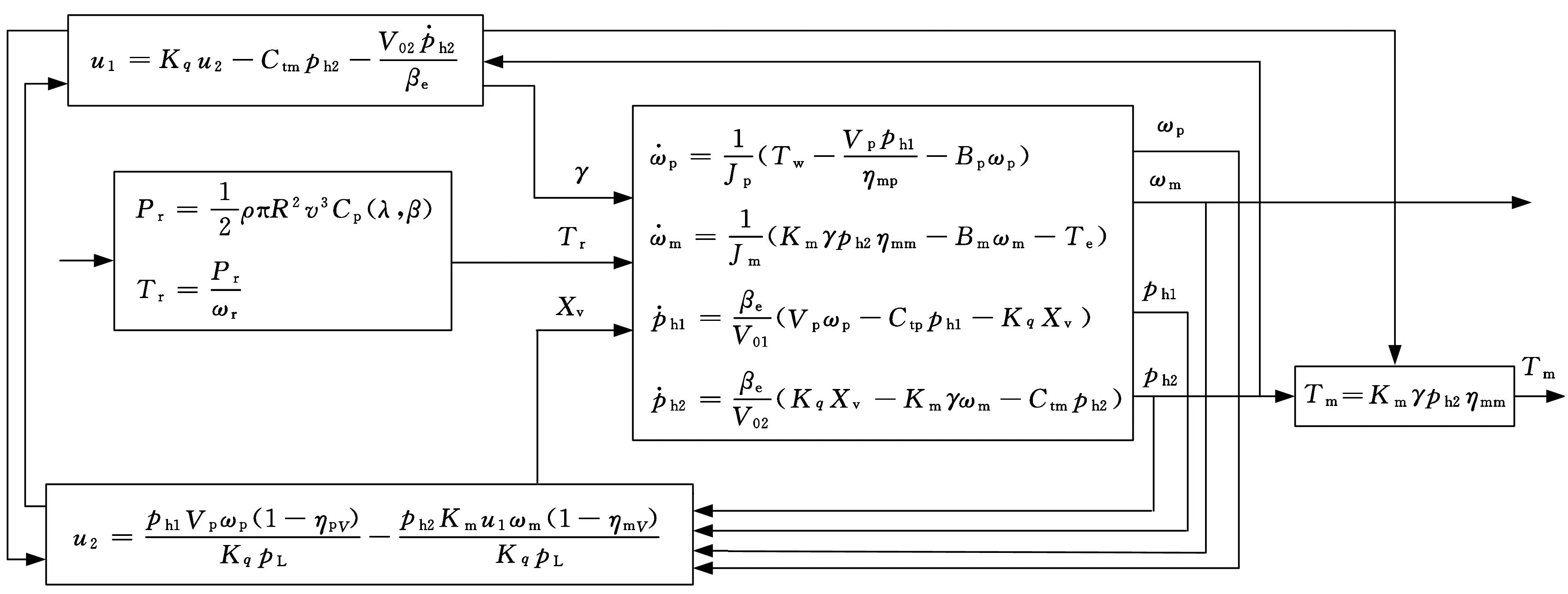
图4　基于转矩和转速联合控制的高电能质量控制仿真模型

该仿真实验平台主要包括风力机模拟部分、液压传动部分、控制部分和并网发电部分，实验平台实物图如图5所示，相应的参数见表1。

图5　实验平台液压系统实物图

风力机额定功率Pr(kW)24定量泵转动惯量Jp(kg·m3)400风力机额定风速vr(m/s)13变量马达排量梯度Km(m3·rad)5.366×106风力机叶轮半径R(m)7.48变量马达阻尼系数Bm(N·m·s/rad)0.0345最大风能利用系数Cpmax0.4496变量马达转动惯量Jm(kg/m3)0.462最佳叶尖速比λmax22.77油液体积弹性模量βe(Pa)743×10-6风力机转速ωr(r/min)762系统泄漏系数Ct(m3/(s·Pa))6.28×10-12定量泵阻尼系数Bp(N·m·s/rad)0.4管路容腔体积V(m3)2.8×10-3定量泵排量Vp(m3·rad)10-5

4.2仿真与实验结果分析

通过仿真模型和实验平台模拟真实风力发电机组工作状况，当定量泵在典型的转速范围内运转时，变量马达输出转速如图6所示。

图6中，当定量泵转速分别在400～410 r/min、600～610 r/min和800～810 r/min范围内变化时，在上述控制器下，变量马达转速的实验曲线是相对平滑的，即系统输出的转速波动小。同时随着定量泵转速的增加，马达转速动态响应速度相对快些，超调量小些，且输出转速实验与仿真曲线最终均稳定于(1500±6)r/min。

当定量泵转速分别为400 r/min、700 r/min和800 r/min三种典型转速时，系统输出转矩如图7所示。

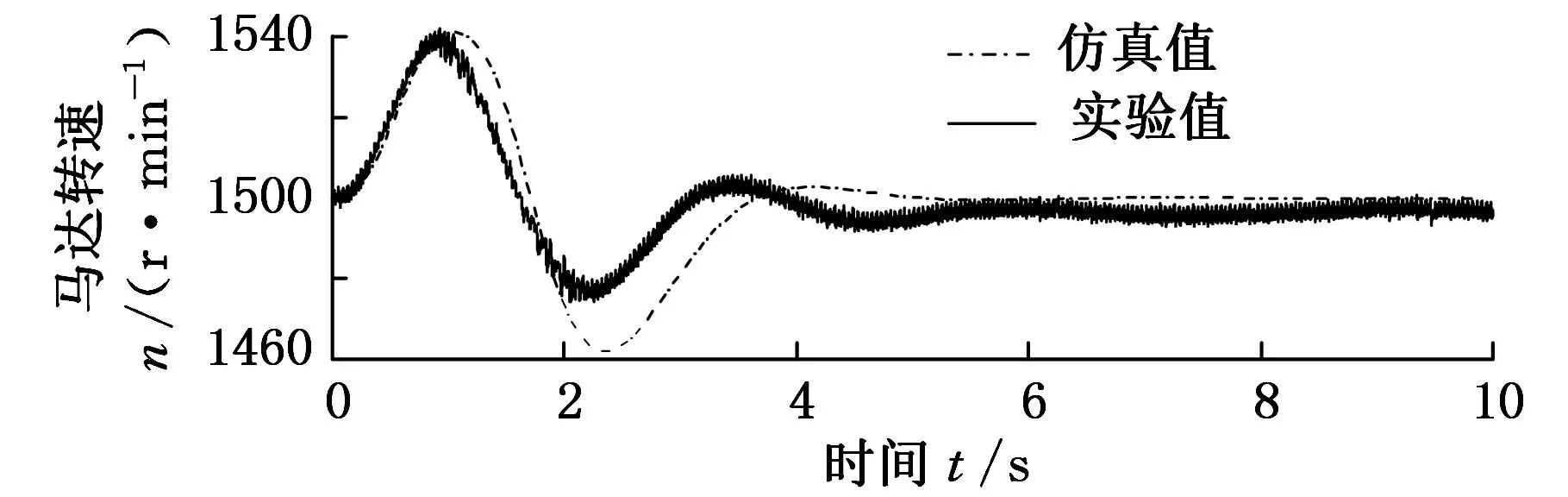
(a)定压泵转速为400～410 r/min

(b)定压泵转速为600～610 r/min

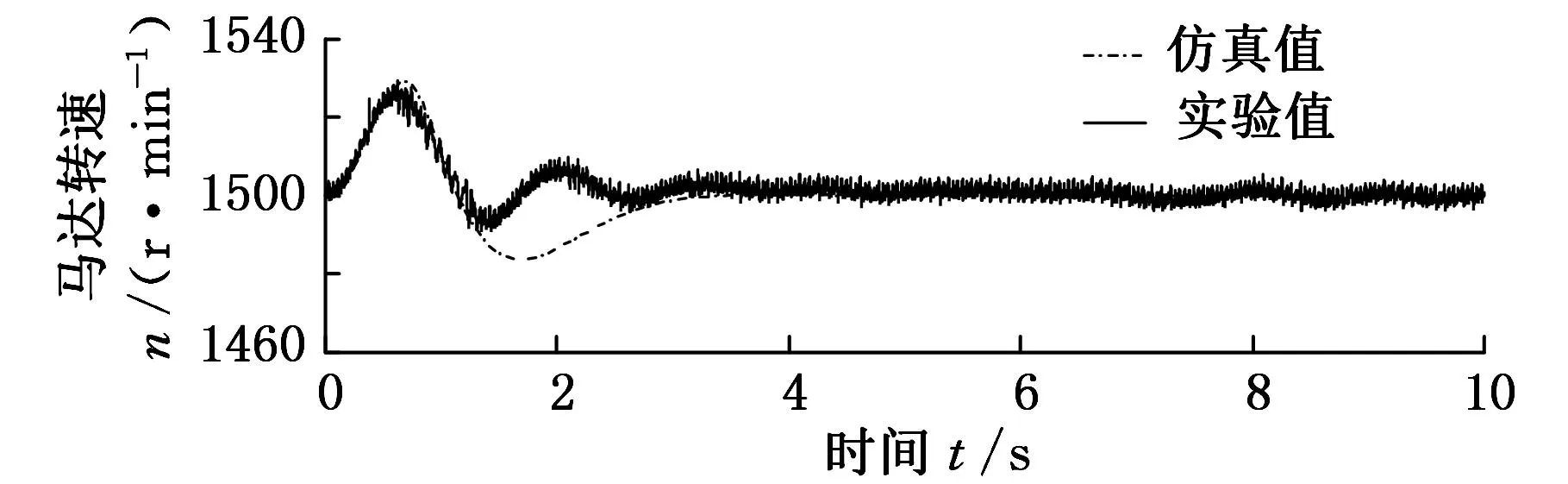
(c)定压泵转速为800～810 r/min图6　变量马达转速的仿真-实验结果

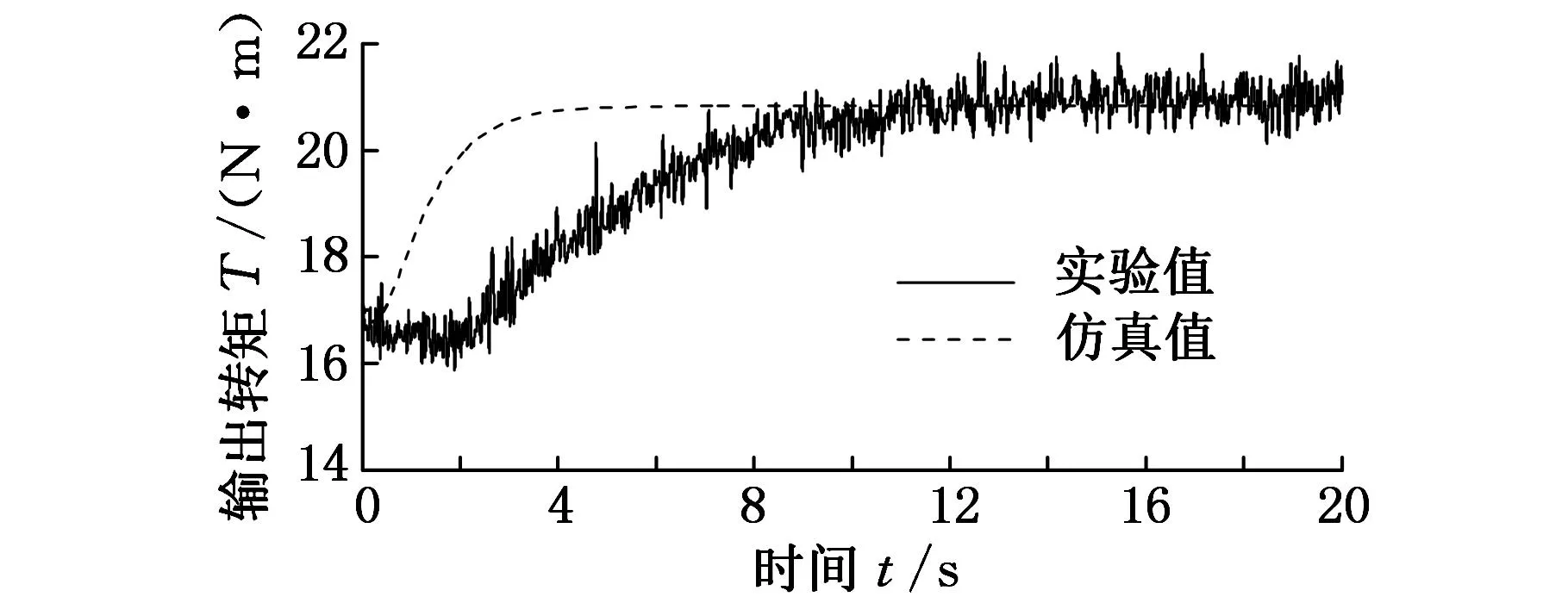
(a)ωm=400 r/min

(b)ωm=700 r/min

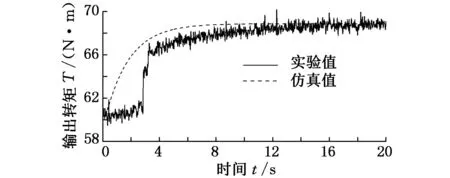
(c)ωm=800 r/min图7　系统输出转矩的仿真-实验结果

由图7可知，当定量泵转速分别为400 r/min、700 r/min和800 r/min时，在上述控制器下，系统输出的转矩相对平滑，且实验曲线最终均能与理论的仿真曲线重合，即采用上述控制器，在不同定量泵转速下，均可以保证转矩控制精度。

5　结语

本文针对液压型风力发电机组的高电能质量控制问题中的关键因素转速和转矩的解耦控制进行研究。首先，进行理论分析，建立定量泵-变量马达液压传动系统数学模型。其次，针对该数学模型存在的双输入双输出耦合问题进行分析，采用前馈补偿解耦控制方法解耦，并提出以比例节流阀开度和变量马达摆角为输入的转速和转矩解耦控制器。最后，以30kVA液压型风力发电机组半物理仿真实验平台为基础，进行仿真与实验研究，将仿真和实验结果进行对比，在不同定量泵转速下，系统输出的转速和转矩都能得到很好的控制效果，并最终重合到一起，从而验证了理论分析的准确性，为液压型风力发电机组的高电能质量的控制提供了理论基础。

[1]International Energy Agency. Global Carbon-dioxide Emissions Increase by 1.0 Gt in 2011 to Record High[EB/OL].[2012-05-24].http://www. iea. org/newsroomandevents/news/2012/may/name_27216_en.html.

[2]Hamzehlouia S, Izadian A.Modeling of Hydraulic Wind Power Transfers[C]//2012 IEEE Power and Energy Conference.Illinois, 2012:1-6.

[3]马伟明, 肖飞．风力发电变流器发展现状与展望[J]．中国工程科学, 2011, 13(1): 11-20.

Ma Weiming, Xiao Fei.The Status and Outlook of Wind Power Converters[J].Engineering Sciences, 2011, 13(1): 11-20.

[4]Jha B, Rao K.Disturbance Rejections and Harmonics Reduction of Doubly-fed Induction Generator Using Robust Controller[C]//Proceedings of 2009 Annual IEEE India Conference.Gujarat,2009: 1-5.

[5]Sainz L, Mesas J.Deterministic and Stochastic Study of Wind Farm Harmonic Currents[J].IEEE Transactions on Energy Conversion, 2010, 25(4): 1071-1080.

[6]孙涛, 王伟胜, 戴慧珠, 等. 风力发电引起的电压波动和闪变[J]. 电网技术,2003, 27(12):62-70.

Sun Tao, Wang Weisheng, Dai Huizhu, et al.Voltage Fluctuation and Flicker Caused by Wind Power Generation[J]. Power System Technology, 2003, 27(12):62-70.

[7]姚俊, 夏先锋, 陈西寅, 等.风电并网用全功率变流器谐波电流抑制研究[J]. 中国电机工程学报, 2012, 32(12):17-25.

Yao Jun, Xia Xianfeng, Chen Xiyin, et al. Harmonic Currents Suppression for Full Size Power Grid-connection Converter Used for Wind Power Generation[J]. Proceedings of the CSEE, 2012, 32(12):17-25.

[8]张坤, 吴建东, 毛承雄, 等. 基于模糊算法的风电储能系统的优化控制[J].中国电机学报, 2012, 27(10) :235-241.

Zhang Kun, Wu Jiandong, Mao Chengxiong, et al. Optimal Control of Energy Storage System for Wind Power Generation Based on Fuzzy Algorithm[J].Transactions of China Electrotechnical Society, 2012, 27(10):235-241.

[9]Jerbi L，Krichen L, Ouali A. A Fuzzy Logic Supervisor for Active and Reactive Power Control of a Variable Speed Wind Energy Conversion System Associated to a Flywheel Storage System[J]. Electric Power Systems Research, 2009, 79(6): 919-925. [10]Denholm P, Sioshansi R. The Value of Compressed Air Energy Storage with Wind in Transmission-constrained Electric Power Systems[J].Energy Policy, 2009, 37 (8): 3149-3158.[11]Ngamroo I. Power Oscillation Suppression by Robust SMES in Power System with Large Wind Power Penetration[J]. Physica：C, 2009, 469(1): 44-51.

[12]Luo Changling, Banakar H, Shen Baike, et al．Strategies to Smooth Wind Power Fluctuations of Wind Turbine Generator[J].IEEE Trans. on Energy Conversion, 2007, 22(2): 341-349.

[13]De Battista H, Mantz R J.Dynamical Variable Structure Controller for Power Regulation of Wind Energy Conversion Systems[J].IEEE Trans. on Energy Conversion, 2004, 19(4): 756-763．

[14]艾超, 叶壮壮, 孔祥东,等. 液压型风力发电机组主传动系统压力控制特性研究[J]. 中国机械工程, 2015, 26(6):729-732.

Ai Chao, Ye Zhuangzhuang, Kong Xiangdong, et al. Pressure Control Characteristics of Main Transmission System of Hydraulic Transmission Wind Energy Conversion System[J]. China Mechanical Engineering, 2015, 26(6):729-732.

(编辑陈勇)

Decoupling Control of Speed and Torque of a Hydraulic Wind Turbine

Zhang Yin1,2Kong Xiangdong1Chen Lijuan1Ai Chao1Li Hao1

1.Yanshan University,Qinhuangdao,Hebei,066004 2.Qinhuangdao Institute of Technology,Qinhuangdao,Hebei,066100

Taking a hydraulic wind turbine as the research object, the high power quality output as a goal, the decoupling control of the speed and torque in the unit was conducted.The mathematical models for the hydraulic transmission system fixed displacement pump-variable motor were established. Based on the hydraulic transmission system, the key factors affecting the quality of the unit electric energy output were explored, the coupling problem of the multiinput-multioutput system was analysed, and the control method of feed-forward decoupling compensation was used to decouple. The control laws of variable motor and proportional throttle valve to the output speed and output power of the hydraulic system were analysed, and the speed and torque decoupling controller was obtained based on high power quality in hydraulic wind turbine. Taking a 30 kVA hydraulic wind turbine semi-physical simulation platform as the simulation and experimental platform, the proposed control method was researched. Simulation analyses and experimental results show that the decoupling control of output speed and torque in hydraulic wind turbine is realized, and the steady speed control of hydraulic transmission system and the smoothing control of transmission power fluctuation may be achieved effectively. The results lay the foundation for the control of high quality electric power output and the improvement of the grid friendly performance in the hydraulic wind turbine.

wind power; hydraulic transmission; constant speed output; power smoothing; decoupling control

2015-07-03

国家自然科学基金资助项目(51375422)；河北省青年基金资助项目(QN20132017)

TH137DOI：10.3969/j.issn.1004-132X.2016.07.017

张寅，男，1979年生。燕山大学机械工程学院博士研究生，秦皇岛职业技术学院机电工程系副教授。研究方向为流体传动及控制。发表论文10余篇。孔祥东(通信作者)，男，1959年生。燕山大学副校长、教授、博士研究生导师。陈立娟，女，1989年生。燕山大学机械工程学院硕士研究生。艾超，男，1982年生。燕山大学机械工程学院副教授、博士。李昊，男，1977年生。燕山大学车辆工程学院副院长兼车辆实验室主任、副教授、博士。