基于CFD的磁流体轴承润滑膜特性分析

李　婷　马吉恩　章　禹　方攸同

浙江大学，杭州，310027



基于CFD的磁流体轴承润滑膜特性分析

李婷马吉恩章禹方攸同

浙江大学，杭州，310027

磁流体轴承具有转速高、密封性好、承载力强等优点，符合高速铁路中的应用需求。提出一种磁流体轴承结构，并运用CFD方法对轴承润滑区的承载性能以及热效应问题进行了仿真计算，在此基础上进一步分析了偏心率对轴承承载力及温升的影响规律，为之后磁流体轴承的进一步设计提供帮助。

磁流体轴承；CFD；气穴模型；润滑特性

0　引言

高速是我国铁路发展的主要方向。为了适应高速牵引电机轴承的高速、重载等使用要求，轴承必须具有优异的密封、振动、温升、承载力等性能指标，才能使工作寿命延长[1]。

磁流体是由纳米级尺寸的磁性固体颗粒经由界面活性剂均匀地分散在液体介质中而形成的一种磁性胶体溶液[2]。这种新型的功能性液体在具备流体特性的同时，也拥有和磁性材料相类似的特性。在外加磁场作用下，其流变性与空间形态能够被控制。磁流体轴承就是利用磁流体的这些特殊性能而发展起来的一种新型轴承。

早在20世纪60年代，已有学者开展磁流体润滑滑动轴承的理论研究。文献[3]开创性地对非均匀磁场作用下的磁流体润滑轴承进行了研究，得到了外加磁场在转动轴上作用的磁悬浮力会使轴承的承载能力提高的结论。文献[4]对磁流体在短轴承中的应用进行了理论研究，研究表明，在一定磁场强度范围内，磁流体的应用令润滑膜的承载能力大大增加，同时轴承的稳定性和刚度也得以提高。文献[5]对耦合应力作用下的磁流体轴承承载能力进行了计算，计算结果显示，端泄会在极大程度上降低润滑膜承载力，高转速则利于全油膜润滑的建立。文献[6]对磁流体轴承的设计以及应用进行了系统概括，并展示了近年来磁流体设计方面的成果。种种研究表明磁流体轴承相对于传统轴承有着更多的优点。

磁流体轴承以磁流体为润滑介质，在外加磁场的影响下，依靠磁流体的自密封能力，可以防止泄漏以及外界污染物进入轴承间隙，故具有良好的密封性；由于磁流体润滑能够提供平稳的低摩擦润滑，且具有良好的可控性，因而振动小；采用磁流体润滑的摩擦因数小，所以发热少；由于存在磁场，使得在高速高温情况下拥有更高的承载力。鉴于以上优点，磁流体轴承非常适合用作高速铁路机车牵引电机轴承。

本文建立了磁流体轴承的三维仿真模型，运用Fluent软件对磁流体轴承润滑区特性进行仿真计算，着重分析润滑区的承载性能以及热效应问题。为了讨论轴承承载力以及温升情况与轴颈偏心变化的关系，分别建立了不同偏心率情况下的磁流体轴承模型，单独改变轴颈偏心量，通过仿真分析其对轴承承载力及温升的影响。

1　磁流体轴承的应用优势和原理

1.1对比普通轴承的应用优势

牵引电机轴承是保证铁路机车安全运行的重要部件之一。对于高速铁路机车牵引电机来说，其转速较高、启动快、运行久，因而对轴承的稳定性有更高的要求[7]。

目前，滚珠轴承应用最为广泛，其在精密程度方面具有一定的优势，但在高速以及高温等特殊工况下工作会产生许多问题。例如，高速情况下会使润滑脂飞溅，磨损加剧，产生振动与噪声；高温情况下润滑油脂破坏会致使轴承寿命缩减等。相比较而言，空气轴承依靠空气不磨损接触件的特性，使得轴承寿命大大延长。但是，空气轴承的刚性不如机械轴承，且对生产制造工艺有很高的要求，并需要无水、无油、无尘的空气。相比于滚珠与空气轴承，普通油膜润滑滑动轴承依靠其较大的黏度而具有更好的抗振能力及承载能力。但是，普通油膜润滑滑动轴承为了实现润滑和散热，需要配置大功率的供油系统来不断注入润滑油，这使系统成本增加的同时也带来了维护和保养的不便。

磁流体轴承是20世纪60年代配合核动力技术而发展起来的新型轴承，是以加入了磁性固体颗粒的载液(即磁流体)作为润滑介质进行润滑的轴承。与传统轴承相比，这种轴承具有一系列特性：①在外加磁场的影响下，依靠磁性固体颗粒表面特殊液态膜的保护而具有更稳定的润滑状态，从而防止端泄以及外界污染物进入轴承间隙，起到自润滑密封的作用；②由于加入到摩擦副中的磁性固体颗粒大小只有5～10 nm，远小于表面粗糙度而一般不会引起磨损，故磁流体润滑能够提供平稳的低摩擦润滑，振动小；③磁流体润滑具有较小的摩擦因数，因而发热少；④能工作于高速高温情况，且由于磁场的存在，轴承承载能力强于同等轴承；⑤在强磁场、低偏心情况下，甚至能做到零泄漏，减少润滑液端泄的同时简化了系统[8-10]。

1.2磁流体轴承的原理

磁流体轴承正常工作所需要的外加磁场一般采用永磁体或直流励磁来激发。前者可以产生磁力线形状规则的稳定磁场，而后者则可以通过改变励磁电流来改变磁场强度，从而进一步改进磁流体的分布。两种磁场激发方式各有优劣。本文主要研究直流励磁磁流体轴承，其结构如图1所示。

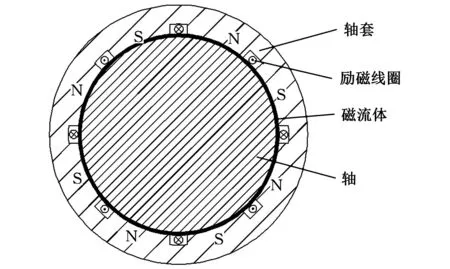
图1　直流励磁磁流体轴承结构

2　模型处理

本文根据高速铁路机车牵引电机的结构，建立了转轴以3000 r/min运行的，考虑偏心的磁流体轴承的三维模型。考虑到轴承周围环境对轴承热效应和热分布的影响，加入了整段安装轴的模型。填充轴承间隙的磁流体材料选用纳米四氧化三铁(Fe3O4)。磁流体润滑膜的厚度为0.05 mm。所建立的三维模型如图2所示。

图2　三维模型

在三维建摸的基础上，完成了对整个模型的网格划分。网格划分主要考虑以下两方面的影响：一方面，要保证网格的密度，特别是关键区域的网格，以确保计算的精度；另一方面，对于外部环境区域里对关键特性分析影响不大的部分需进行网格数目的降低，以提高仿真计算的速度。根据以上两条原则，对磁流体润滑膜处的剖分采用等分形式并进行加密。轴套及安装轴承的该段轴采用渐进网格的形式。其中，对于轴套的剖分，采用沿径向由外到内网格逐渐变细，而对于安装轴承的该段轴则采用沿径向由外到内网格逐渐变粗。网格剖分结果如图3所示。

图3　网格剖分结果

3　边界条件的施加

3.1热边界条件

工程中传热现象从物理本质上区分时，通常有三种基本形式，即热传导、对流换热及辐射换热。热传导是指热量由高温物体传向低温物体或者由同一物体的高温部分传向低温部分的能量交换过程，可以在固体、液体以及气体中发生，是固体传热最主要的方式；对流换热是指在用流体的宏观流动将所含热能从物体中一处迁移到另一处的过程中，流动的流体与其所经固体表面之间所发生的热交换过程，一般可分为自然对流和强迫对流两种方式；辐射换热则是指高温物体以电磁波形式传递热量的过程[11]。本文所研究的电机采用强制对流的冷却方式，辐射换热可以忽略不计;由于磁流体润滑属于流体动压润滑状态，以对流散热为主要方式，传导散热通常可以不予考虑。

在本文计算中，将轴承安装位置的该段轴设置为对流换热边界条件，由于轴的温度变化相对并不明显，故将其他与轴承相距较远的几段轴设置为恒温边界条件，将轴的外表面和磁流体润滑膜的内表面，轴套的内表面和磁流体润滑膜的外表面设置为流固耦合面，并将前者设置为旋转壁面，转速与轴颈转速相同，为3000 r/min，后者设定为固定壁面边界条件。

开启能量方程，由于是黏性流动，故在能量方程中考虑黏性生成热(viscous heating)。

3.2空化边界条件

滑动轴承内的空穴现象，主要是因为溶解在润滑液内的空气由于外界压力变低，其体积膨胀析出而造成[12-13]。当考虑润滑膜的空化效应时，压力达到一定值后润滑膜中就可能会有气泡出现，此时轴承间隙处的流动是一种多相流，需要考虑气相和液相之间的相互耦合作用，因此需要引入多相流模型。本文选用Mixture多相流模型以及Zwart-Gerber-Belamri空化模型。

4　不考虑空化的润滑膜压力和温升分析

在上述网格划分以及边界条件设置的基础上，不开启空化模型，从主轴壁面开始初始化，使用Fluent进行迭代求解直至收敛，可得到磁流体润滑膜的压力以及温度云图，以偏心率ε=0.5时的工况为例的压力和温度云图如图4、图5所示。图6为轴承内理论润滑膜压力分布。

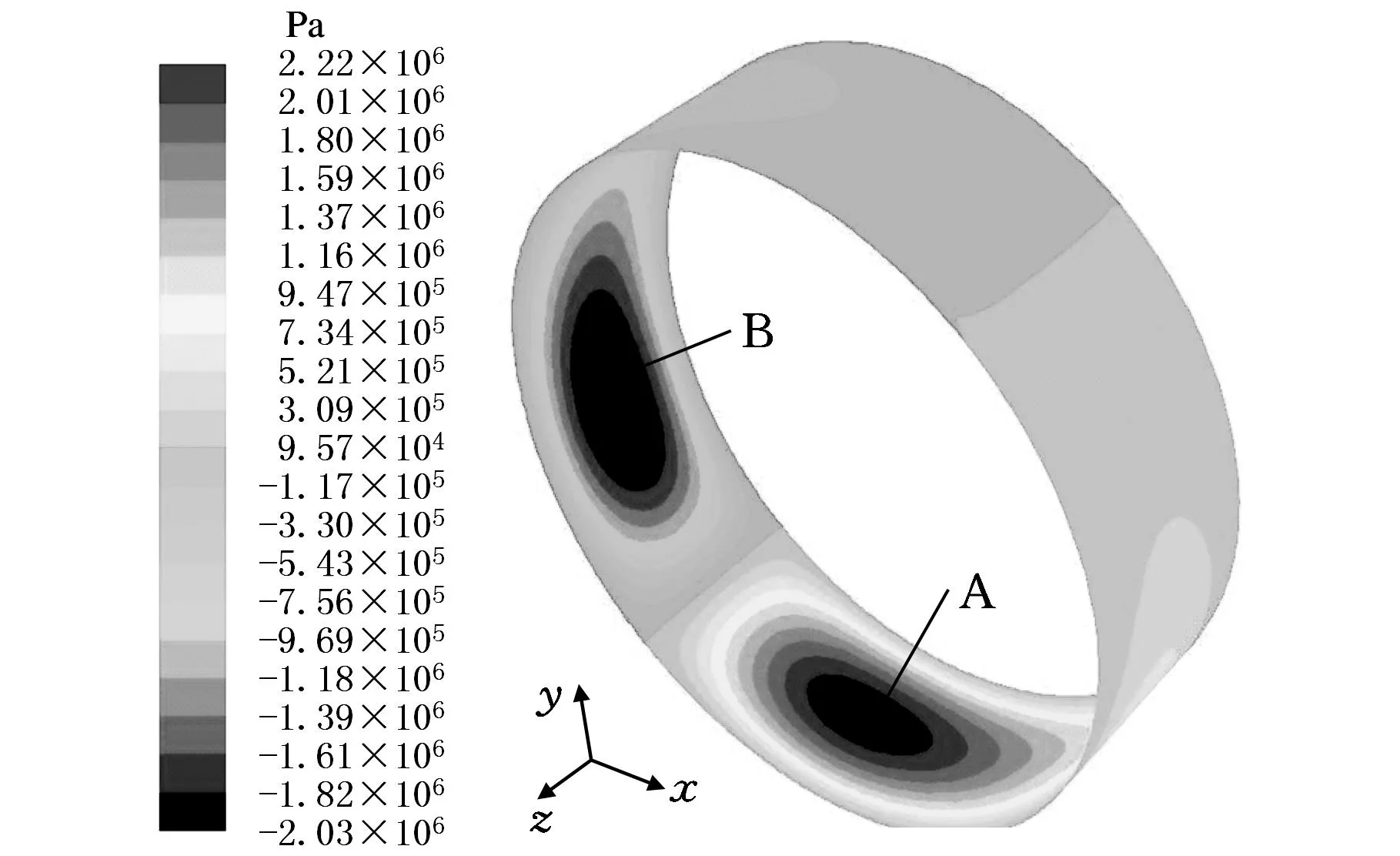
图4　磁流体润滑膜压力云图

图5　磁流体润滑膜温度云图

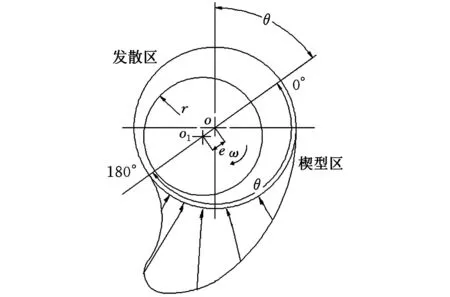
图6　轴承内理论润滑膜压力分布

由图4可知，润滑膜压力分布有两个非常明显的压力集中区，一个呈现正压，一个呈现负压，在最小润滑膜厚度区被明显地分隔开来。由于轴的偏心和顺时针转动，在A区域产生了收敛楔形，从而产生了磁流体润滑膜的正压力。在收敛区，随着间隙的减小，压力逐渐增大达到正压峰值后减小，通过最小油膜厚度处后进入发散区(B区域)，此时由于润滑膜速度迅速增大，很快形成了一个真空区域，达到负压峰值，之后逐渐恢复到正压，趋于平稳。这与图6所示的轴承内理论润滑膜压力分布规律一致。磁流体润滑膜中间位置沿周向压力分布曲线如图7所示(此处起点位置与图6不同，故角度不作对应)。正压区域最大压力为2 224 565 Pa，负压区最大压力为2 033 140 Pa，在正压力和负压力的共同作用下，产生承载力来支撑轴颈，并平衡外载荷。由Fluent计算水膜合力大小为2169.2 N。

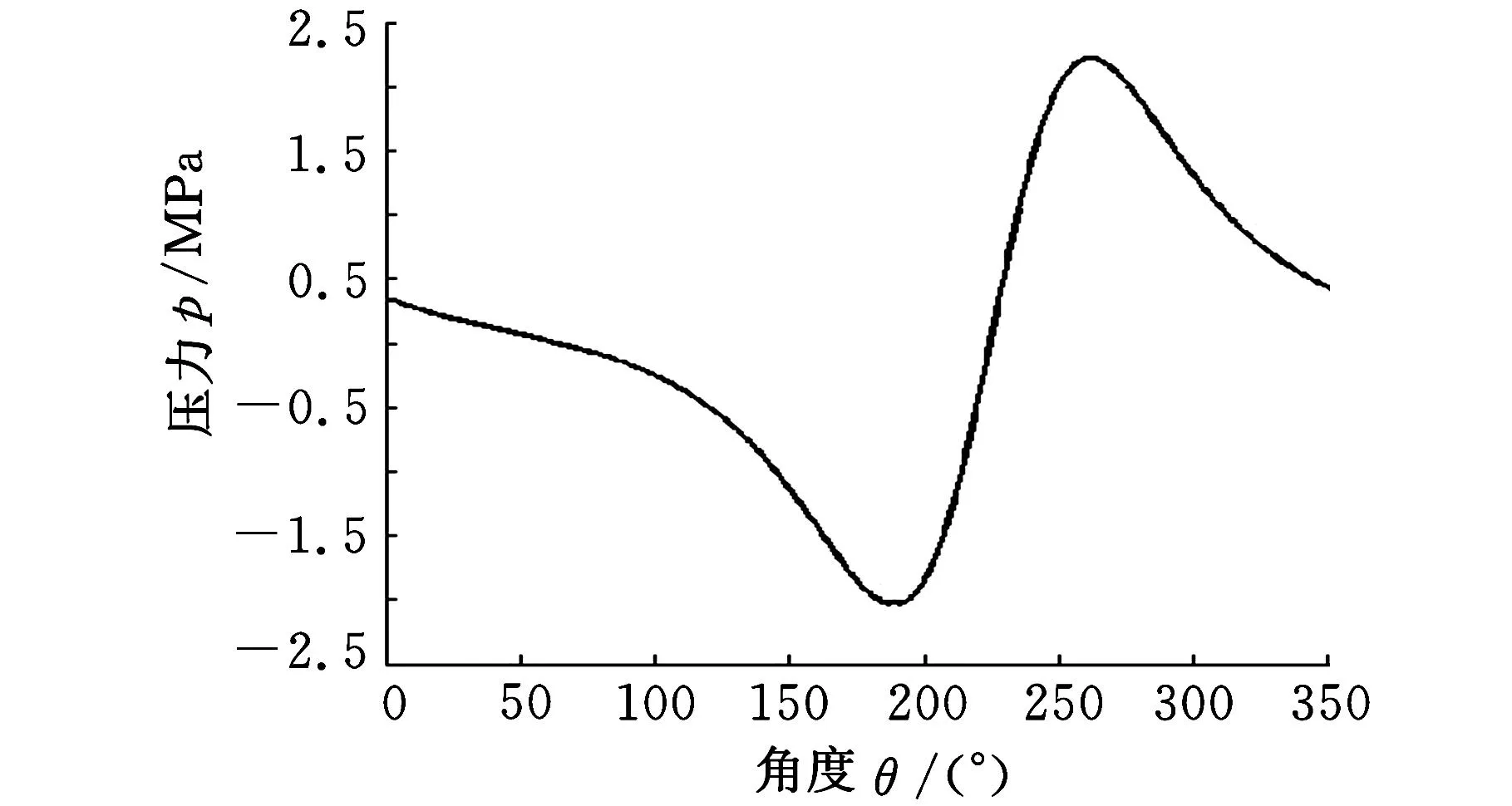
图7　润滑膜中心面周向压力分布

图5所示为转速3000 r/min时的三维温度场分布云图。由图可知，发散区(C区域)的最高温度为98.3 ℃，离开此区域，润滑膜温度开始逐渐降低。可以看到，发散区的温度普遍偏高，且同收敛区的温差约为20 ℃。润滑膜温度沿轴向从中间向两端逐渐降低，温度分布在36～80 ℃范围内。可知，磁流体润滑膜处的热量在轴向方向上，沿轴向两端散热情况良好。

5　加入空化模型的润滑膜压力和温升分析

由于发散区负压的存在，当压力达到一定值，润滑膜中就可能会有气泡出现，引起气穴现象。这将导致润滑膜在负压区迅速破裂并进一步对压力分布产生影响。因此在计算时加入空化模型是很有必要的。

本文选用Mixture多相流模型以及Zwart-Gerber-Belamri空化模型进行了仿真计算。初始设置时将磁流体相体积分数设为100%，空气相体积分数设为0，最终通过仿真得到最后的空气体积分数。图8～图12为不同偏心率ε下的磁流体润滑膜压力分布云图。

图8　ε=0.1下的磁流体润滑膜压力分布云图

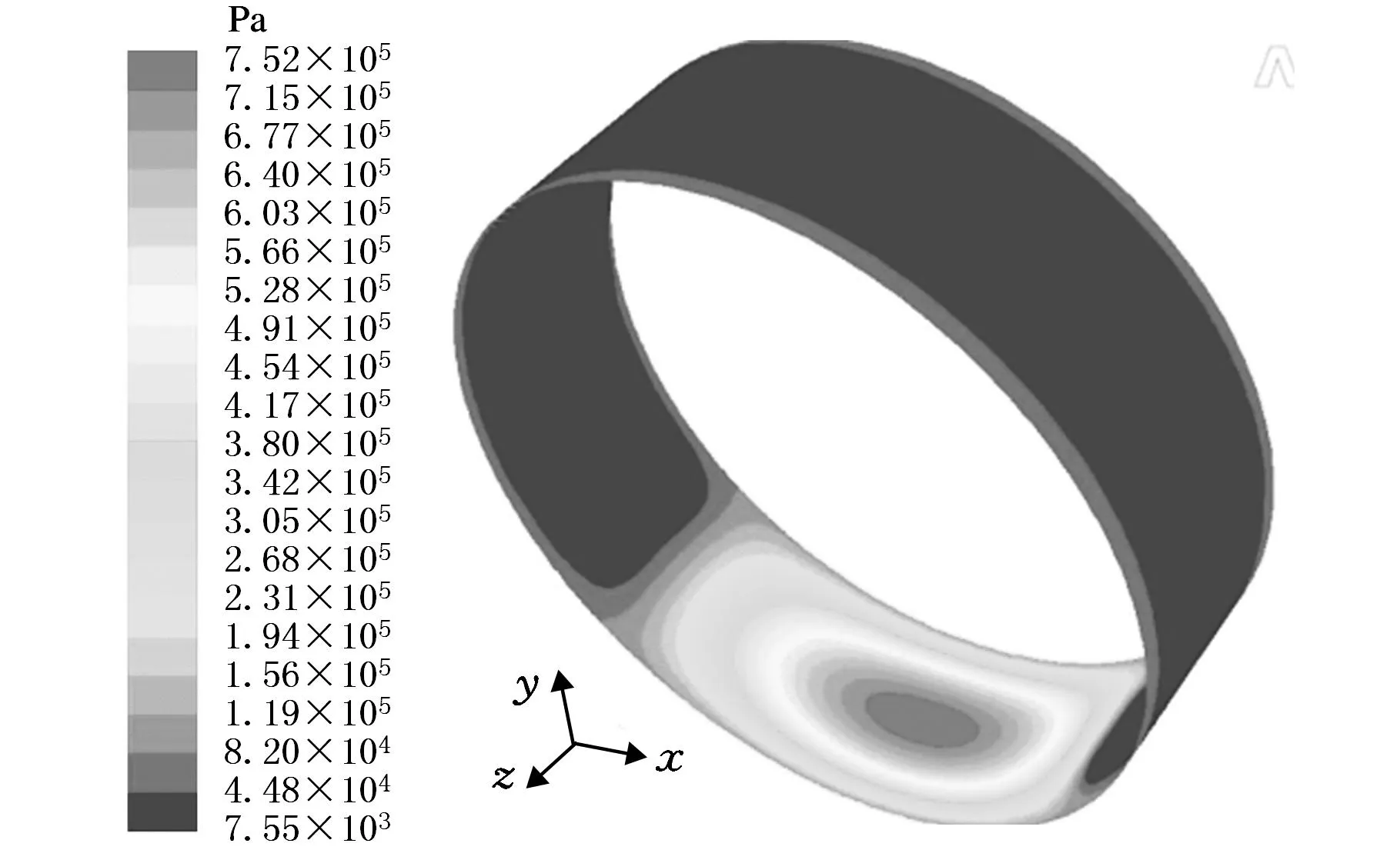
图9　ε=0.3下的磁流体润滑膜压力分布云图

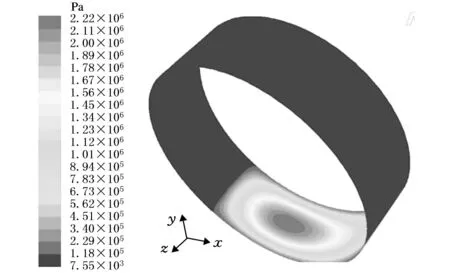
图10　ε=0.5下的磁流体润滑膜压力分布云图

图11　ε=0.7下的磁流体润滑膜压力分布云图

图12　ε=0.9下的磁流体润滑膜压力分布云图

对比图4与图8c可以看出，没有采用空化模型时，润滑膜在发散阶段的最小压力达-2.03 MPa，这与实际情况完全不符，而采用空化模型的计算结果更符合实际。

在仿真实验中得知，加入空化模型后，在收敛区内，随着间隙的减小，压力升高，在最小间隙前某一角度，压力达到最大值，之后压力有所下降。当经过最小间隙进入发散区后，随着间隙变大，由于油膜破裂，没有产生负压，而只有很小的正压，并且压力基本保持不变，其值为7550 Pa。随着偏心率的增大，正压区域内的压力峰值随之增大，高压区范围越来越小。这是由于润滑膜产生楔形的直接原因是轴颈的偏心，偏心距的增大会使得磁流体润滑膜的楔形效应增强，从而提高了磁流体润滑膜的承载力。润滑膜最大压力与偏心率之间的规律曲线如图13所示。

图13　磁流体润滑膜最大压力与偏心率的关系

从偏心率0.5工况下的磁流体润滑膜气相体积分布的仿真可知，在收敛区内，几乎全部润滑面上都有完整的磁流体膜。当经过最小间隙进入到发散区后，随着间隙的变大，在某一角度油膜开始破裂。并且油膜气化比例随着间隙的变大而增大。磁流体润滑膜气相体积分数如图14所示。

图14　磁流体润滑膜气相体积分数(ε=0.5)

图15为加入空化模型后，偏心率0.5工况下的磁流体润滑膜温度分布云图。与图5对比可知，考虑空化后，润滑膜的最高温度由98.3 ℃下降到了76.6 ℃，高温区仍然出现在发散区范围内，但所占面积有所减小。整体来看，散热情况较图5更为良好。

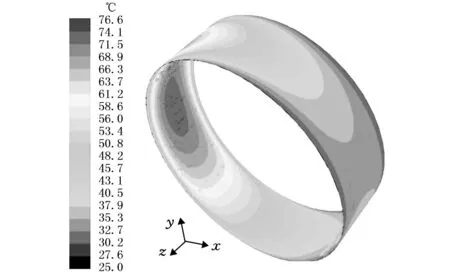
图15　考虑空穴效应的温度分布云图(ε=0.5)

6　结论

(1)对比了磁流体轴承相对于其他轴承的应用优势，分析了其用作高速铁路机车牵引电机轴承的理论可行性。

(2)提出了一种磁流体轴承结构，建立了其三维模型并进行了网格剖分，应用CFD方法对模型进行了仿真分析，得到了轴承润滑膜温度和压力的分布规律，验证了模型的合理性。

(3)考虑了滑动轴承内的空穴效应，为了找到磁流体润滑膜承载性能和轴颈偏心之间的关系，建立了不同偏心率的润滑膜模型，通过仿真，分析了不同偏心率下磁流体润滑膜作用力的变化规律。

[1]何强, 李安玲, 张继祝,等. 高速列车轴承的发展趋势[J]. 徐州工程学院学报(自然科学版), 2012, 27(1):58-64.

He Qiang, Li Anling, Zhang Jizhu, et al. The Development Trend of High-speed Railway Bearing[J]. Journal of Xuzhou Institute of Technology(Natural Sciences Edition), 2012, 27(1):58-64.

[2]顾红, 王先逵, 祝琳华,等. 磁流体技术及发展方向综述[J]. 昆明理工大学学报(理工版), 2002, 27(1):55-57.

Gu Hong, Wang Xiankui, Zhu Linhua, et al.The Review of Magnetic Ferrofluid Technology Development and Its Application[J]. Journal of Kunming University of Science and Technology(Natural Science Edition), 2002, 27(1):55-57.

[3]Tarapov I E. Movement of a Magnetizable Fluid in the Lubricating Layer of a Cylindrical Bearing[J]. Magnetohydrodynamics, 1972(8):444-448.

[4]Tipei N. Theory of lubrication with Ferrofluids: Application to Short Bearings[J]. ASME, 1982,104:510-515.

[5]Das N C．A Study of Optimum Load-bearing Capacity for Slider Bearings Lubricated with Couple Stress Fluids in Magnetic Field[J]. Tribology International, 1998,31(8)：393-400.

[6]Ochonski W.Sliding Bearings Lubricated with Magnetic Fluids[J].Industrial Lubrication and Tribology,2007,59(6):252-265.

[7]施洪生, 张奕黄,高培庆. 高速牵引电机轴承关键技术的发展趋势[J]. 机车电传动, 2007(2): 1-5.

Shi Hongsheng, Zhang Yihuang, Gao Peiqing. Development Trend of Critical Technologies for Bearing of High-speed Traction Motor[J]. Electric Drive for Locomotive, 2007(2):1-5.

[8]王建梅, 孙建召, 薛涛,等. 磁流体润滑技术的发展[J]. 机床与液压, 2011, 39(6):109-112.

Wang Jianmei, Sun Jianzhao, Xue Tao, et al. The Development of Magnetic Fluid Lubricating Technology[J]. Machine Tool & Hydraulics, 2011, 39(6):109-112.

[9]王瑞金, 王常斌. 磁流体技术的工业应用[J]. 力学与实践, 2004, 26(6):8-13.

Wang Ruijin, Wang Changbin.The Industrial Apllications of the Magnetic Fluid Technique[J]. Mechanics and Engineering, 2004, 26(6):8-13.

[10]何世权,杨逢瑜,杨瑞. 滑动轴承磁流体薄膜和润滑特性的研究[J]. 润滑与密封, 2007,32(1):126-128.

He Shiquan,Yang Fengyu,Yang Rui. Research on Lubricating Characteristic of Thin Film and Glide Bearings Affected by Magnetic Fluid[J]. Lubrication Engineering, 2007,32(1):126-128.

[11]魏永田, 孟大伟, 温嘉斌. 电机内热交换[M]. 北京：机械工业出版社, 1998.

[12]Guo Zenglin, Hirano T, Kiyk R G. Application of CFD Analysis for Rotating Machinery—Part I: Hydrodynamic, Hydrostatic Bearings and Squeeze Film Damper[J]. J. of Engineering for Gas Turbines and Power APRIL, 2005,127:445-451.

[13]张楚, 杨建刚, 郭瑞,等. 基于两相流理论的滑动轴承流场计算分析[J].中国电机工程学报,2010,30(29):80-84.

Zhang Chu, Yang Jiangang, Guo Rui, et al. Simulation of Journal Bearing Flow Field Using Computational Fluid Dynamics Two Phase Flow Theory[J]. Proceedings of the CSEE, 2010,30(29):80-84.

(编辑郭伟)

Lubrication Characteristics Analyses of Ferrofluid Bearing Based on CFD Simulation

Li TingMa JienZhang YuFang Youtong

Zhejiang University,Hangzhou,310027

Ferrofluid bearing had a series of advantages, like high speed, good sealing, strong bearing capacity, etc.,which complied the needs of high-speed railway. A three-dimensional model of ferrofluid bearing was built and the simulation about the bearing and thermodynamic characteristics were carried out based on CFD. And then, further analyses of the influences of eccentricity were made, which laid the foundation for subsequent design of ferrofluid bearing.

ferrofluid bearing; computational fluid dynamics(CFD); cavitation model; lubrication performance

2015-03-29

国家自然科学基金资助项目(51105331, 51177144)；国家高技术研究发展计划(863计划)资助项目(2011AA11A101)

TH133.3;TH117.2DOI：10.3969/j.issn.1004-132X.2016.07.015

李婷，女，1990年生。浙江大学电气工程学院硕士研究生。主要研究方向为磁流体轴承。马吉恩，女，1979年生。浙江大学电气工程学院助理研究员。章禹，男，1993年生。浙江大学电气工程学院本科生。方攸同，男，1962年生。浙江大学电气工程学院教授。