高频磁场下铝基复合材料熔体中颗粒相的受力与迁移行为模拟
2016-08-16王宏明瞿长晨李桂荣李沛思范晓建江苏大学材料科学与工程学院江苏镇江212013
王宏明,瞿长晨,李桂荣,李沛思,范晓建(江苏大学 材料科学与工程学院,江苏 镇江,212013)
WANG Hongming,QU Changchen,LI Guirong,LI Peisi,FAN Xiaojian(School of M aterials Science and Engineering,Jiangsu University,Zhenjiang 212013,China)
高频磁场下铝基复合材料熔体中颗粒相的受力与迁移行为模拟
王宏明,瞿长晨,李桂荣,李沛思,范晓建
(江苏大学 材料科学与工程学院,江苏 镇江,212013)
根据电磁学的基本原理,采用数值模拟方法计算得出金属熔体表面的磁感应强度,导出电磁体积力与表面磁感应强度,颗粒迁移速度与电磁体积力以及颗粒迁移偏移角度与电磁体积力的关系表达式。研究结果表明:颗粒相迁移行为的影响因素包括电流强度和频率、颗粒粒径等;高度对电磁体积力的有效作用范围为20~100 mm,并在80 m处取得最大值,增大电流,颗粒沿高度方向分布更均匀。
高频磁场;铝基复合材料;颗粒相;迁移
WANG Hongming,QU Changchen,LI Guirong,LI Peisi,FAN Xiaojian
(School of M aterials Science and Engineering,Jiangsu University,Zhenjiang 212013,China)
颗粒增强铝基复合材料具有密度小、强度高、高温性能好以及耐磨性、热稳定性和低膨胀系数优良等优点,具有广阔的应用前景。铝基复合材料中增强相的分布对材料的凝固组织及其性能具有重要影响,控制复合材料凝固过程中颗粒相的迁移行为成为该类复合材料制备的关键问题之一。为了研究控制颗粒相的分布, 王春江等[1-2]研究了强磁场下金属凝固过程中第二相的迁移行为,证明洛伦兹力是促进第二相在基体中均匀分布的重要因素。郭庆涛等[3-5]提出了高频磁场电磁净化技术中电磁体积力的数学模型,并分析了熔体内部电磁体积力的分布规律。然而,对高频磁场下金属熔体凝固过程中颗粒相的迁移规律的研究仍未完善。本文作者用模拟方法分析高频磁场下影响颗粒相迁移行为的因素及作用规律。
1 物理模型与参数
利用ANSYS有限元分析软件计算结晶器内合金熔体表面的磁感应强度。圆坯结晶器的内径为76 mm,外径为92 mm,计算长度为110 mm。结晶器壁上有6条均匀分布的1 mm宽竖直切缝,切缝长度为90 mm,螺线管的半径为50 mm,长度为67 mm;合金熔体和空气的相对磁导率为1,结晶器、合金熔体和空气的电阻率的分别为1×10-8,2.83×10-8和1×1020Ω·m。由于计算区域的对称性,可取整个区域的1/6作为实际计算区域,建立如图1所示物理模型[6],并通过建立圆柱坐标系(r,θ,z)表示空间的位置点。
高频磁场激励电流为正弦交流电,电流密度变化范围为5×106~5×107A/m2,频率为5~20 kHz。合金熔体的密度为2.37 t/m3,三氧化二铝的密度为3.9 t/m3,真空磁导率μ0=4π×10-7H/m,熔体的磁化率为1.05×10-6H/m,熔体的动力学黏度η= 4.5 mPa·s,熔体的磁导率μ0=4π×10-7H/m,熔体的电导率为4.132 2×10-6S/m。
网格划分采用的是ANSYS自带的网格划分工具MeshTool,在计算区域自动生成网格,如图2所示。考虑高频磁场在结晶器壁及熔体内出现集肤效应,在集肤层内至少要划分2层单元以确保计算精度,根据δ=(πμσω)-1/2计算集肤深度δ[7](其中,ω为角频率)。
设定边界条件:1)在模型的对称面上设定磁力线平行边界条件;2)在线圈直径5倍处设定远场边界;3)对结晶器分瓣体和熔体分别设定开路及短路导体条件。

图1 物理模型示意图Fig.1 Schematic of physical modal
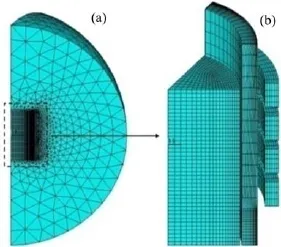
图2 模型的网格划分Fig.2 Meshes of model
2 数学模型的建立
2.1电磁场数学模型
根据Maxwell方程组[8],熔体凝固过程中电磁场计算的控制方程为:
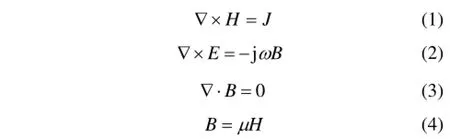
式中:
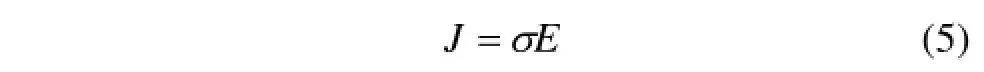
H为磁场强度;B为磁感应强度;J为电流密度;E为电场强度;▽为拉普拉斯算子。
在一定频率下,对于垂直入射导体表面的电磁波,Maxwell方程可以表示为:
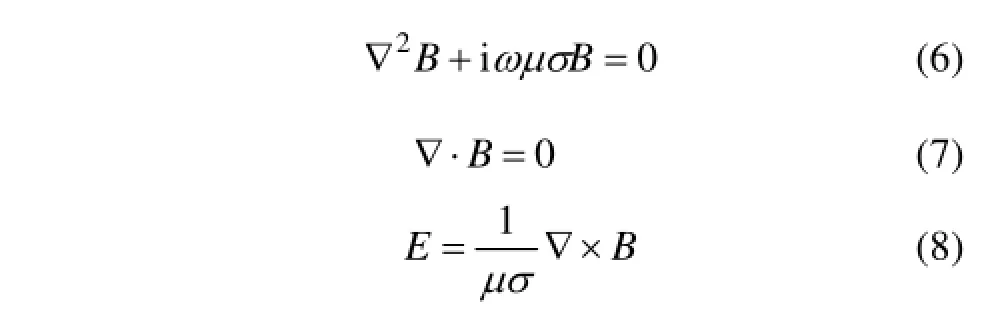
由于高频磁场在金属溶液内存在集肤效应,电磁场在金属中按指数规律衰减,金属熔体内的磁感应强度[4]为
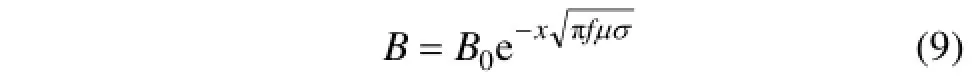
式中:B0为熔体表面处的有效磁感应强度;x为熔体内任一点距离熔体表面的距离;f为电磁场频率。
设通电螺线管的半径为R,长度为L,单位长度的匝数为n,通电电流为I,螺线管(直角坐标系)放置[9]如图3所示。由于螺线管具有对称性,故只需计算xOz平面内的磁场分布,且x和z分量分别是径向和轴向分量。
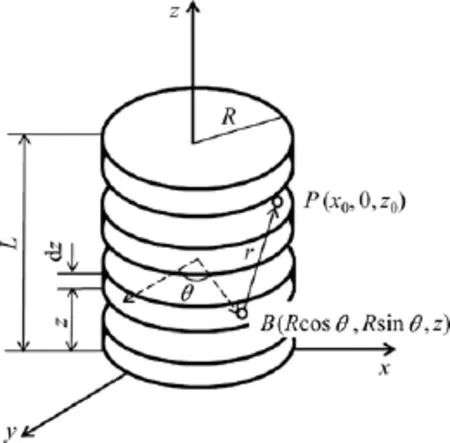
图3 螺线管位置Fig.3 Location of solenoid
在xOz平面内任取1点P(x0,0,z0),在z轴上z点处取厚度为dz的环,则该环的电流为Iˊ=nldz,并在该环上点B(Rcosθ,R sinθ,z)处取电流元I ˊdl[9]为
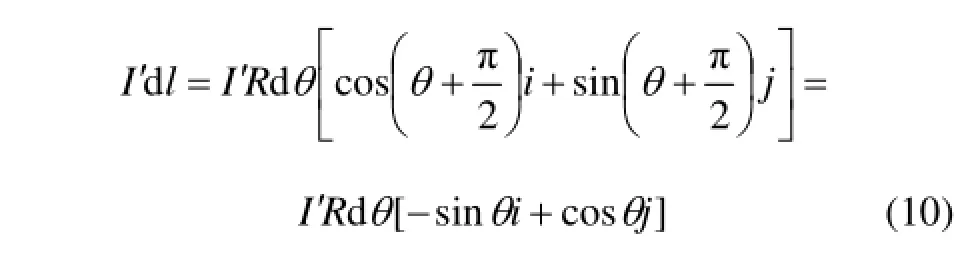
电流元到点P的位置矢量r为
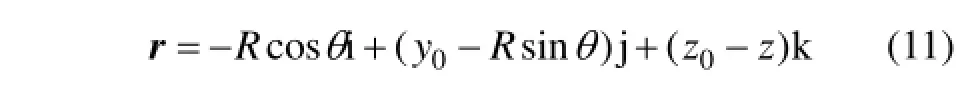
根据比萨定律[10]可得电流元lI dˊ在点P(x0,0,z0)产生的磁感应强度dB:
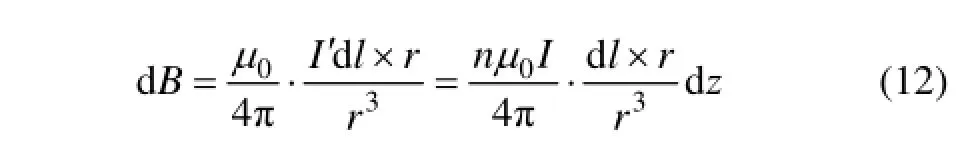
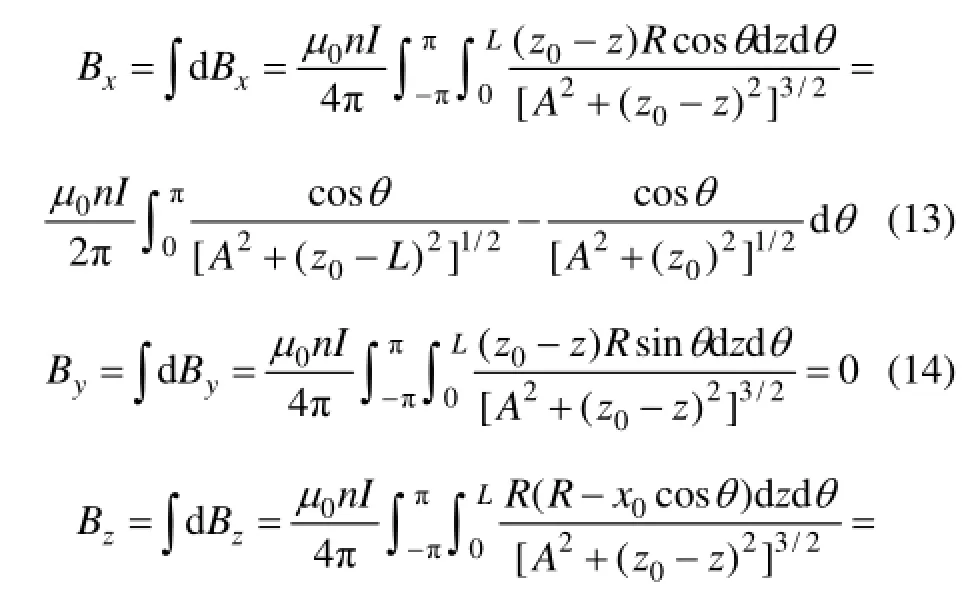
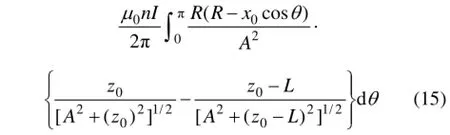
对于螺线管轴线上的点x0=0,则有A2=R2,分别代入式(13)和(15)得:
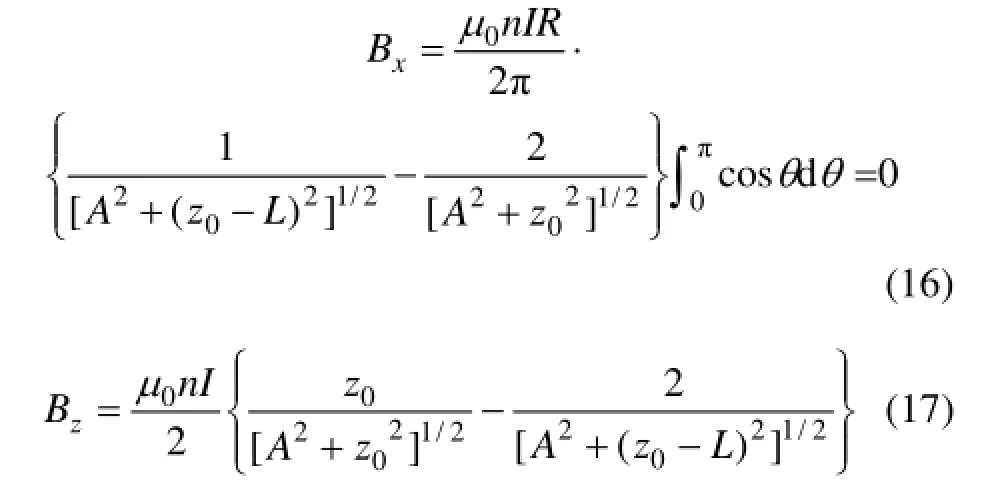
将式(16)和(17)代入式(9)得
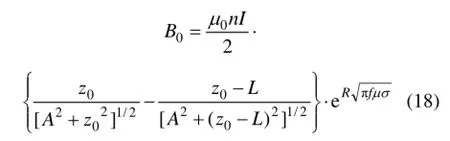
2.2颗粒相受力数学模型
对含有颗粒相的金属熔体中施加高频磁场时,由于高频磁场与感应电流相互作用时会产生电磁力,且电磁力只在导电性良好的熔体中产生,在导电性差的颗粒相中并不产生,因此,颗粒相就受到与电磁力方向相反的电磁挤压力。假设金属熔体的流动速度很小,则电磁场在导电率不同的颗粒相中产生的电磁挤压力可由LEENOV和KOLIN公式[13]计算得出:
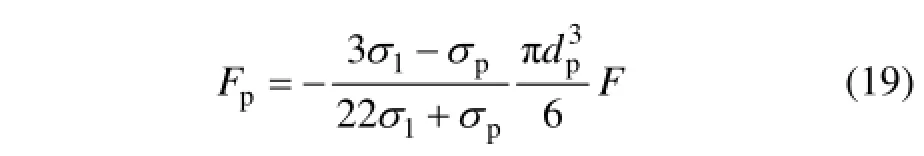
由于非金属颗粒相的电导率趋于0 S/m,则式(19)可变为
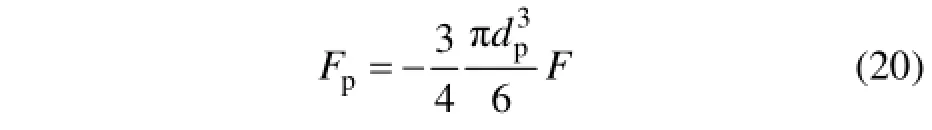
式中:Fp为电磁挤压力;1σ为金属熔体电导率;pσ为颗粒相电导率;dp为颗粒相直径;F为电磁体积力。根据麦克斯韦方程组可得出熔体所受的电磁体积力[4]为
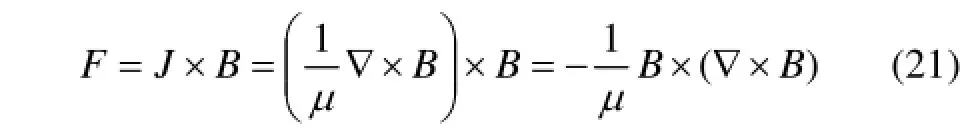
在理想的长直螺线管内,磁感应强度[4]为:
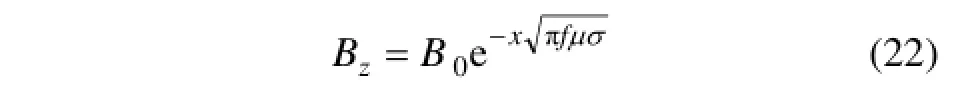
将式(22)代入式(23),可以得到径向的电磁体积力[4]公式:
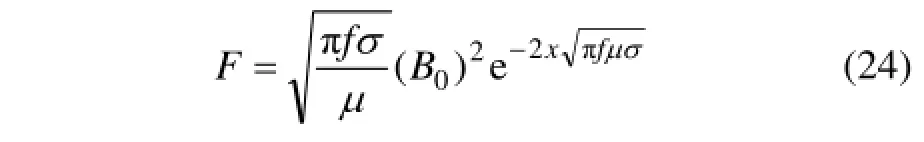
将铝基复合材料熔体置于高频磁场B中,此时熔体中的颗粒相受到的力包括重力Fg、阿基米德浮力Ff、电磁挤压力Fp、黏滞阻力Fv,将这些力分解在竖直方向和水平方向,由于螺线管具有对称性,故只需计算xOz平面内熔体中颗粒相的迁移行为。颗粒相在高频磁场中受力如图4所示。综合在x和z轴上的合力Fx=Fp,Fz=Fg+Ff,若其合力Fx和Fz不等于0,则熔体中的颗粒相会在合力的作用下发生运动,颗粒相会对周围的熔体产生挤压和黏滞作用,因此,磁场内运动的颗粒相的受力可表示如下。
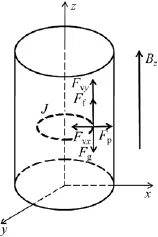
图4 高频磁场下颗粒迁移行为示意图Fig.4 Principle of particle migration behavior with high frequency magnetic field
在x轴上,
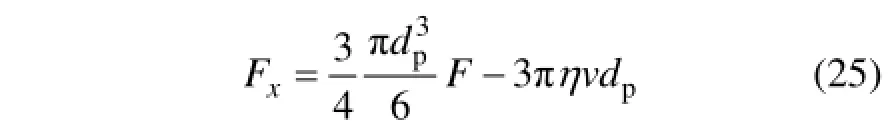
在z轴上,
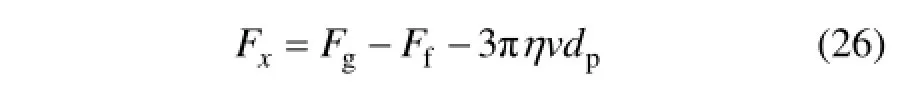
2.3颗粒相运动数学模型
根据牛顿定律,颗粒相在高频磁场下水平方向的力学微分方程[14]为
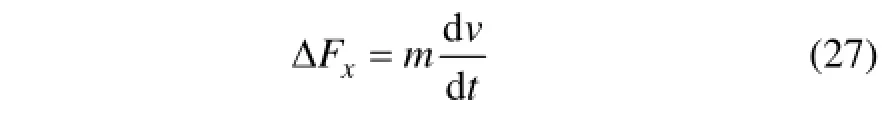
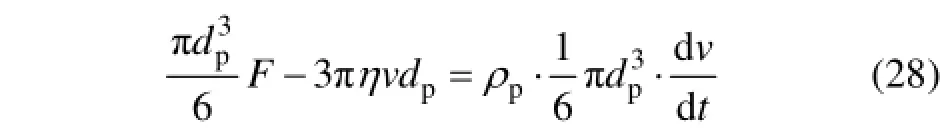
在短时间内,假设电磁力保持不变,根据分离变量法[14],可求解(28)式,得到迁移速度的解析解:
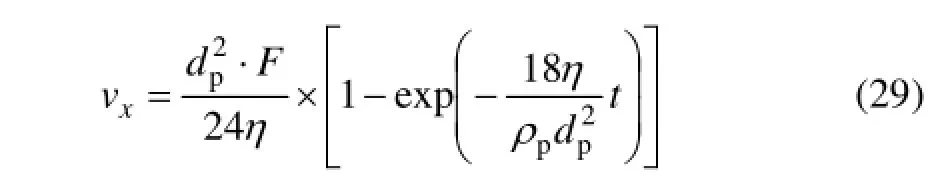
同样,在z轴上,颗粒迁移速度的解析解为
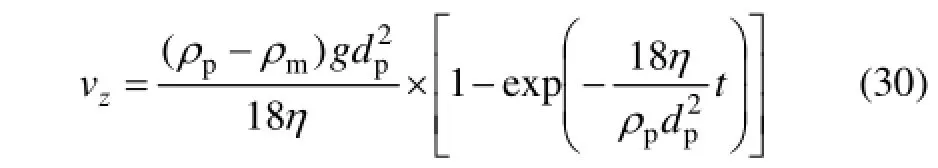
假设熔体的初始状态是静止的,即有vx=0,vz=0,当合力F≠0时,颗粒相在合力F的作用下开始加速运动,随着颗粒相运动速度的增加,运动阻力逐渐增大,其所受合力逐渐减小;当阻力增大到与动力相等即合力F=0时,颗粒相的速度达到平衡速度,系统达到平衡;此时,颗粒相的速度vx和vz可根据式(30)推导得到:
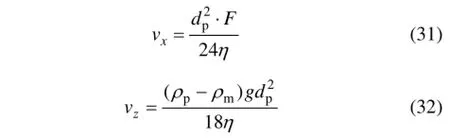
通过计算颗粒在受力平衡时其速度的方向确定颗粒的迁移方向。颗粒的速度方向可用下式表示:
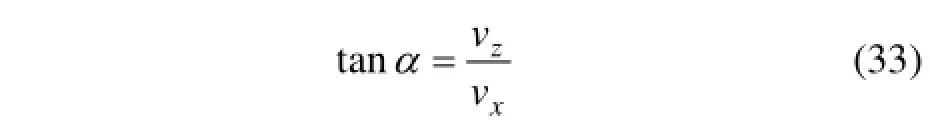
其中:α为颗粒速度方向与水平方向所成的夹角。将式(31)和(32)代入式(32),得
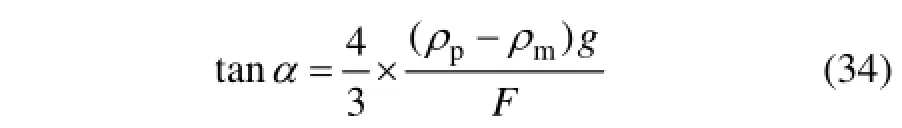
3 计算结果及分析
3.1不同电磁参数下熔体表面磁感应强度的分析
图5所示为不同电流频率下,熔体表面内磁感应强度沿结晶器分瓣体中心高度分布。从图5可看出:在熔体内部磁感应强度随电流密度的增大而增大;在熔体底部到顶部,磁感应强度先增大后减小,且在距离熔体顶部5 mm处,磁感应强度达到最大值;电流频率越高,熔体内磁感应强度越大,当频率增大到10kHz后,磁感应强度的增大趋势趋于缓慢。
3.2不同电磁参数下熔体内电磁体积力的分析
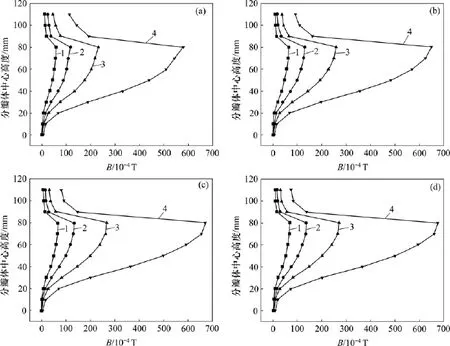
图5 不同电磁参数下熔体表面磁感应强度沿高度的分布规律Fig.5 Distribution law of magneticflux densityalong height directionwith different electromagnetic parameters
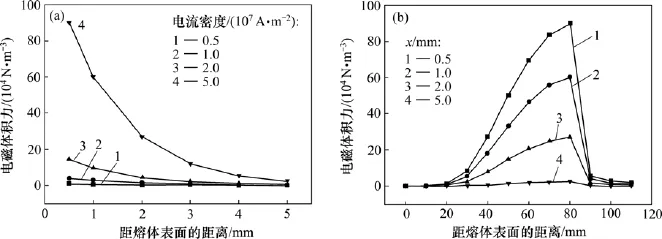
图6 不同电流密度下颗粒所受电磁体积力沿径向和高度方向的分布规律Fig.6 Distribution law of e lectromagneticbodyforcealong heightand radius directionwith different intensitiesof current
图6所示为不同电流强度和不同频率下颗粒所受电磁体积力沿径向和高度方向分布,其中,图6(a)所示为电流频率为10 kHz,在不同电流下粒径为10 μm的颗粒在距结晶器底部80 mm平面内不同位置所受的电磁力沿径向分布图。从图6(a)可知:随着电流密度增大,所产生的电磁力也随之相应增大,且在电流密度增大到107A/m2后,电磁力的增加幅度急剧增大;随着与熔体表面的距离增大,电磁体积力呈指数降低;当与金属熔体侧表面的距离增大到5 mm后,电磁力的下降趋势开始趋于缓慢。图6(b)所示为电流密度为5×107A/m2,频率为10 kHz时,粒径为10 μm颗粒在距熔体表面内不同距离所受电磁体积力沿高度方向分布。由图6(b)可知:电磁体积力的有效作用范围为20~100 mm,且电磁体积力随高度增加而先增大后减小,在80 mm处取得最大值。
3.3颗粒相迁移行为分析
3.3.1颗粒相迁移速度
图7所示为在电流频率为10 kHz、不同电流下,距结晶器底部80 mm平面内不同位置处粒径为10 μm颗粒相迁移速度曲线。由图7可知:增加电流密度会增大颗粒迁移速度;距熔体表面距离x越大,颗粒迁移速度越小,经过约0.000 06 s后,不同位置处颗粒的迁移速度趋于平衡速度vx。
图8所示为不同粒径颗粒相在电流密度为5×107A/m2、电流频率为10kHz 时,距结晶器底部80mm平面内不同位置处迁移速度的曲线。由图8可知:颗粒粒径越大,熔体中颗粒的迁移速度越大,且达到平衡速度所需时间越长。
3.3.2颗粒相的迁移方向
图9所示为电流频率为10 kHz、不同电流密度下,熔体内部不同位置处颗粒在竖直方向和水平方向的速度之比即tanα。由图9可知:熔体自上向下,颗粒在竖直方向和水平方向的速度之比是先减小后增大;增大电流密度会减小颗粒在竖直和水平方向的速度之比,则颗粒迁移方向向下偏移程度就减小,进而导致颗粒沿高度方向分布更均匀。
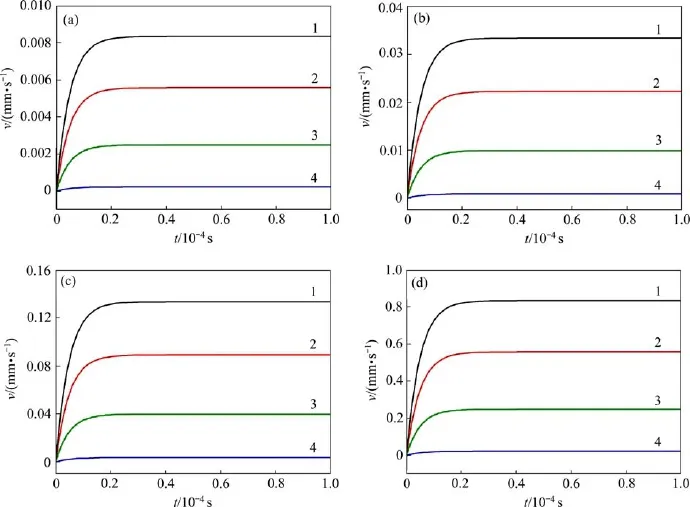
图7 不同电流强度下颗粒迁移速度沿径向的变化规律Fig.7 Distribution law of velocityof particle migrationalong radius directionwith different intensitiesof current
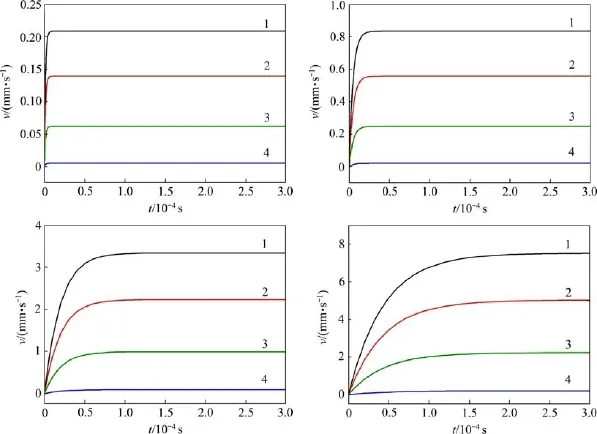
图8 不同颗粒粒径下颗粒迁移速度沿径向的变化规律Fig.8Distributionlawofvelocityof particle migrationalong radius directionwith different particlesizes
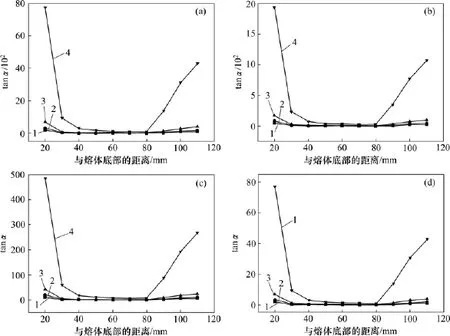
图9 不同电流强度下颗粒迁移方向偏移角度沿高度方向的变化规律Fig.9Distributionlawofangleof particle migration offsetalong height directionwith different intensitiesof current
4 结论
1)在高频磁场下,熔体中电磁体积力在高度方向上有效作用范围为20~100 mm,且随高度增加电磁体积力而先增大后减小,并在80 mm处取得最大值。电磁体积力自表面向内部呈指数衰减。
2)通过控制颗粒相在熔体中的迁移速度来实现其分布。影响颗粒迁移速度的因素包括电流强度和频率、颗粒相的粒径等。增大电流密度、颗粒粒径可增大颗粒迁移速度。在电流密度为5×107A/m2、频率为10 kHz时,粒径为30 μm的颗粒在距熔体表面0.5 mm处,其迁移速度可达到7.51 mm/s。
3)在高频磁场下,熔体自上向下,颗粒迁移方向向下偏移程度先减小后增大。增大电流密度,颗粒迁移方向向下偏移程度减小,当电流密度达5×107A/m2时,距熔体底部30~90 mm范围内,颗粒几乎不发生偏移,颗粒沿高度方向分布更均匀。
[1]王春江,苑轶,刘铁,等.强磁场条件下金属凝固过程中第二相的迁移行为[J].物理学报,2010,59(5):3116-3121. WANG Chunjiang,YUAN Yi,LIU Tie,et al.Effect of high magnetic field on the migration of second phases during the solidification of metals[J].Acta Physica Sinica,2010,59(5): 3116-3121.
[2]王春江,王强,王磊,等.利用强磁场控制SiCp/Al复合材料增强颗粒分布状态[J].铸造,2007,56(5):467-472. WANG Chunjiang,WANG Qiang,WANG Lei,et al.Control of reinforced particles distribution in SiCp/Al composites using high magnetic fields[J].Foundry,2007,56(5):467-472.
[3]郭庆涛,金俊泽,李廷举.高频磁场电磁净化试验研究及净化时间的计算[J].铸造,2005,54(7):670-673. GUO Qingtao,JIN Junze,LI Tingju.Experiment research of electromagnetic elimination of nonmetallic particles from liquid metal by imposition of high frequency magnetic field and theoretical calculation of elimination time[J].Foundry,2005, 54(7):670-673.
[4]郭庆涛,金俊泽,李廷举.高频磁场电磁净化体积力模型建立[J].稀有金属材料与工程,2007,36(5):849-852. GUO Qingtao,JIN Junze,LI Tingju.Mathematical model of body force in electromagnetic purification at magnetic field of high frequency[J].Rare Metal Materials and Engineering,2007, 36(5):849-852.
[5]曹志强,陈飞,王同敏,等.高频磁场下制备颗粒增强铝基梯度复合材料[J].铸造,2011,60(6):549-553. CAO Zhiqiang,CHEN Fei,WANG Tongmin,et al.Fabrication of particle reinforced aluminum matrix gradient composite under highfrequencymagneticfield[J].Foundry,2011,60(6): 549-553.
[6]王宏明,刘强,李桂荣,等.磁场频率对软接触结晶器内磁感应强度分布的影响[J].特种铸造及有色合金,2008,28(1): 20-22. WANG Hongming,LIU Qiang,LI Guirong,et al.Effects of electromagnetic field frequency on magnetic induction density distributioninsoft-contactmold[J].SpecialCasting& NonferrousAlloys,2008,28(1):20-22.
[7]王宏明,王庆富,徐明喜,等.软接触电磁连铸技术的研究进展[J].铸造技术,2006(1):32-35. WANGHongming,WANGQingfu,XUMingxi,etal. Developmentofsoft-contactelectromagneticcontinuous casting[J].Foundry Technology,2006(1):32-35.
[8]夏小江,王宏明,戴起勋,等.电磁软接触连铸高频磁场的数值模拟[J].中国有色金属学报,2008,18(3):529-534. XIA Xiaojiang,WANG Hongming,DAI Qixun,et al.Numerical simulation of high frequency magnetic field for electromagnetic soft-contact continuous casting[J].The Chinese Journal of Nonferrous Metals,2008,18(3):529-534.
[9]惠小强,陈文学.有限长通电螺线管空间的磁场分布[J].物理与工程,2004,14(2):22-26. XI Xiaoqiang,CHEN Wenxue.The magnetic field of limited solenoid with electric current[J].Physics and Engineering,2004, 14(2):22-26.
[10]李春生,杨中海,黄桃.有限长通电螺线管空间磁场分析[J].现代电子技术,2008,32(11):28-30. LI Chensheng,YANG Zhonghai,HUANG Tao.Magnetic field analysis of limited solenoid with electric current[J].Modern Electronics Technique,2008,32(11):28-30.
[11]刘耀康.螺线管磁场的数值解[J].高师理科学刊,2008, 28(11):60-64. LIU Yaokang.The numerical solution of the magnetic field induced by a solenoid[J].Journal of Science of Teachers’College and University,2008,28(11):60-64.
[12]王国强.螺线管磁场的另一计算方法[J].高等函授学报(自然科学版),2003,16(2):14-16. WANG Guoqiang.Another calculation method of the magnetic field induced by a solenoid[J].Journal of Higher Correspondence Education(Natural Sciences),2003,16(2):14-16.
[13]LEENOV D,KOLIN A.Theory of electromagnetophoresis(Ⅰ): magnetohydrodynamic forces experienced by spherical and symmetrically oriented cylindrical particles[J].J Chem Phys, 1954,22(4):683-688.
[14]晋芳伟,任忠鸣,任维丽,等.强梯度磁场下金属熔体中析出相晶粒迁移的动力学研究[J].物理学报,2007,56(7): 3851-3859. JIN Fangwei,REN Zhongming,REN Weili,et al.On dynamics of precipitated grains migrating in molten metal under high gradient magnetic field[J].Acta Physica Sinica,2007,56(7): 3851-3859.
[15]钟云波,任忠鸣,邓康,等.金属净化技术的一种革命性方法:电磁净化法[J].包头钢铁学院学报,1999,18(增刊):363-368. ZHONG Yunbo,REN Zhongming,DENG Kang,et al.An innovative way to purifying liquid metals-by electromagnetic field[J].Journal of Baotou University of Iron and Steel Technology,1999,18(Suppl):363-368.
(编辑陈灿华)
Simu lation on force and movement behavior of particles in alum inum matrix com posite melt under high-frequency magnetic field
According to thebasic principlesof electromagnetic,the magnetic flux density on the surfaceof themetalmelt was calculated through numerical simulation method.The relational expression of the electromagnetic body force and the magnetic flux densitywas deduced.Furthermore,the relational expressionsof the velocity of particle migration,theangle of the particle m igration offset and the electromagnetic body force were deduced.The results show that the main influential factors of particle migration behavior include the current intensity,frequency and particle size.The effect of the heighton electromagnetic body forces is from 20mm to 100mm.Especially the electromagnetic body force reaches the maximum value at 80 mm.W ith the increase of the current intensity,the distribution of particles along the height direction becomesmore uniform.
high frequency magnetic field;alum inum matrix composites;particle phase;m igration
王宏明,副教授,硕士生导师,从事金属基复合材料研究;E-mail:ujswang@sina.com
TG249.6;TG244.3
A
1672-7207(2016)07-2205-08
10.11817/j.issn.1672-7207.2016.07.004
2015-07-18;
2015-09-22
国家自然科学基金资助项目(51371091,51174099);江苏省自然科学基金资助项目(BK2011533)(Projects(51371091, 51174099)supported by the National Natural Science Foundation of China;Project(BK2011533)supported by the Natural Science Foundation of Jiangsu Province)
