上证指数的影响因素分析

胡人友

(马鞍山中加双语学校　安徽马鞍山　243000)



上证指数的影响因素分析

胡人友

(马鞍山中加双语学校安徽马鞍山243000)

摘要：采用统计分析，对影响上证指数的因素做了分析，采用多元回归，建立了上证指数的多元线性模型。通过模型回归值与上证指数的相对误差数据分析，回推出重大政策事件对上证指数的影响。说明在股市投资中，既要重视数据挖掘，借鉴回归模型，同时也需要高度关注政策事件对股市变化的影响。

关键词：上证指数；数据挖掘；因素分析；主成分分析；多元线性回归

股票做为一种金融产品，是大众参与度极高的理财工具。如何对海量的股市数据和信息做基本处理和分析，以降低投资风险是十分重要的一项财商技能。

股市的变化受到多种因素的影响：如政策因素，经济因素，市场因素，地区因素，全球因素，企业自身因素等。股市的风险分为系统风险和非系性风险。系统风险影响到整个股市的波动，股市表现出一致的走向，大盘呈现出牛熊的态势变化。政治，经济，政策等都是导致系统性风险的诱因。非系统风险与整个市场波动无关，为某一企业或某一行业特有的风险，如单个企业自身的经营运作情况、出台的产业政策对涉及到相关企业的影响等等。

系统风险关系到整个证券市场的波动，不是通过分散投资可以弥补的，它直接影响到投资者的股市收益及本金。通过历史数据分析，寻找判断的参考依据，在牛熊市转化前成功地抛出股票，锁定收益率或在熊市加剧前止损，对于散户个人来说非常重要。股市蕴藏着大量的数据信息，通过对股票市场的大数据进行挖掘，进行深入的分析和加工，获得影响股市变化的共同性因素。对这些因素加以重点关注，并根据其所反映出的规律，用作股市变化判断的基本依据，进行股票投资的操作，从而实现规避本金和收益遭受损失的可能性。

1　宏观经济因素对上证指数的影响及多元回归模型的建立

上证指数是上海证券交易所编制的股票指数，于1990年12月9日正式开始发布，它的变化反映着整个股票市场行情的变化。国家的经济政策和经济指标对上证指数的走势产生不同程度的影响。例如调整存款准备金率和再贴现率等都会影响着货币供给量，继而影响到证券市场的资金量。

1.1指标数据对上证指数的影响分析

消费指数：CPI消费者物价指数，通货膨胀水平的一个量化。PPI：生产者物价指数衡量商品生产阶段的价格变化。CPI-PPI的差值反映的是企业盈利水平。CPI-PPI的差值降低，说明企业经营成本提高，企业利润下降； CPI-PPI的差值增大，则表明企业经营成本降低，利润在增加。

国家经济指标：GDP国内生产总值，是国家宏观经济增长的体现。进出口总额同比增长，反映对外贸易的总规模。

货币供应量指标因素：存款准备金，金融机构为保证客户提取存款和资金清算需要而准备的在中央银行的存款，可以影响金融机构的信贷扩张能力，从而间接调控货币供应量。利率作为经济指标之一，也是影响货币供应量的一个重要因素。M1-M2同比增长率的差值是股市资金供应的一个直接表现量。 若M1(狭义货币供应量)-M2(广义货币供应量)的差值增大，说明存款活期化，可用作投资的资金面增加。若M1-M2的差值减少，则表明企业和居民选择将资金以定期的形式存在银行，流动资金减少。

大众心理及市场多空活跃度表现因素： 融资余额和融券余额差值表明市场做多、做空力量的差异。

1.2上证指数影响因素多元回归模型的建立

1.2.1多元线性回归初始模型

在进行上证指数影响因素多元回归时，需要选定作为自变量的影响因素。本文选择如下因素(见表一)作为自变量，采用多元回归工具[1]进行回归，并对其回归系数进行显著检验，大多数回归系数不能通过t检验。说明其变量之间存在多重共线性，构造出来的模型稳定性差，需要重新选择变量，构建新的回归模型。

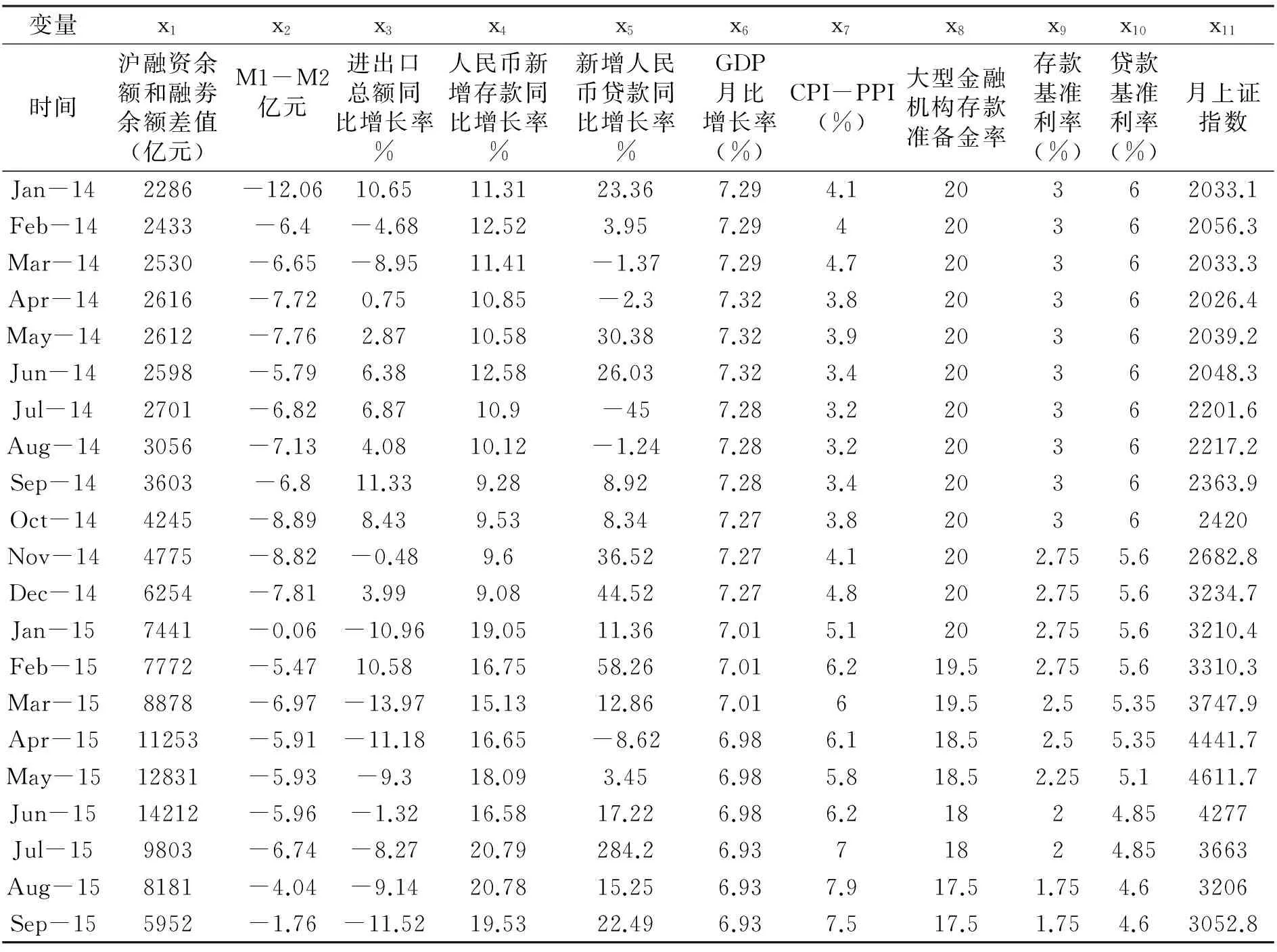
表1　2014年1月至2015年9月上证指数影响因素原始数据

1.2.2主成分分析消除多重共线性，重建回归模型

通过主成分分析将多个变量转化为少数几个互相无关的综合变量，消除变量之间的多重共线性。

图1　碎石图

根据特征值的累计百分率超过方差贡献的百分数85%，选择4个主成分, 碎石图见图1。

主成分表达式如下：

F1=0.305043*x1+0.2265202*x2-0.268039

*x3+0.3517024*x4+0.1429947*x5-0.362127*x6+0.3583347*x7-0.347691*x8-0.358158*x9-0.361862*x10

F2=0.07635514*x1-0.5772297*x2+0.3285513

*x3-0.0629*x4+0.71925865*x5+0.026*x6+0.0676*x7-0.1019076*x8-0.0927*x9-0.0867*x10

F3=-0.388538349*x1+0.477823835*x2-0.239022143*x3+0.232796412*x4+0.630848574*x5+0.0338*x6-0.0367*x7+0.23*x8+0.169848928*x9+0.164884252*x10

F4=-0.1071797*x1+0.43838322*x2+

0.86026821*x3+0.14854684*x4-0.0453*x5-0.0951*x6-0.000344*x7-0.1290782*x8-0.0661*x9-0.0455*x10

本文根据上述四个主成分生成自变量和因变量数据表格(表二)，并据此数据重建多元回归线性模型。从多元线性模型的四个综合成分自变量的回归系数显著性检验的结果来看， t 分布临界值为t0.025(16)=2.119，而F1自变量的t检验值为2.098不能通过回归系数检验,其余主成分满足显著性t检验。

1.2.3建立符合要求的多元回归线性模型

将主成分变量F1剔除，构建以F2，F3和F4为自变量的回归模型，方程式如下：

Y=49.5958-12.6504*F2-3.8138*F3-4.7181*F4。回归系数通过t0.025(17)=2.101的检验，表明主成分变量F2，F3 和F4 显著。其偏相关系数分别为-0.9268，-0.9221和-0.9541，表明上证指数对F2，F3和F4的依赖程度均高，且对F4的依赖度略高一些。回归方程的F统计量为665，大于F(3,17)=3.20(5%的显著水平)，说明回归方程的回归拟合效果显著。模型的复相关系数R2为0.9916，说明方程的拟合度很高。模型计算结果和实际上证指数的对比结果见表2。

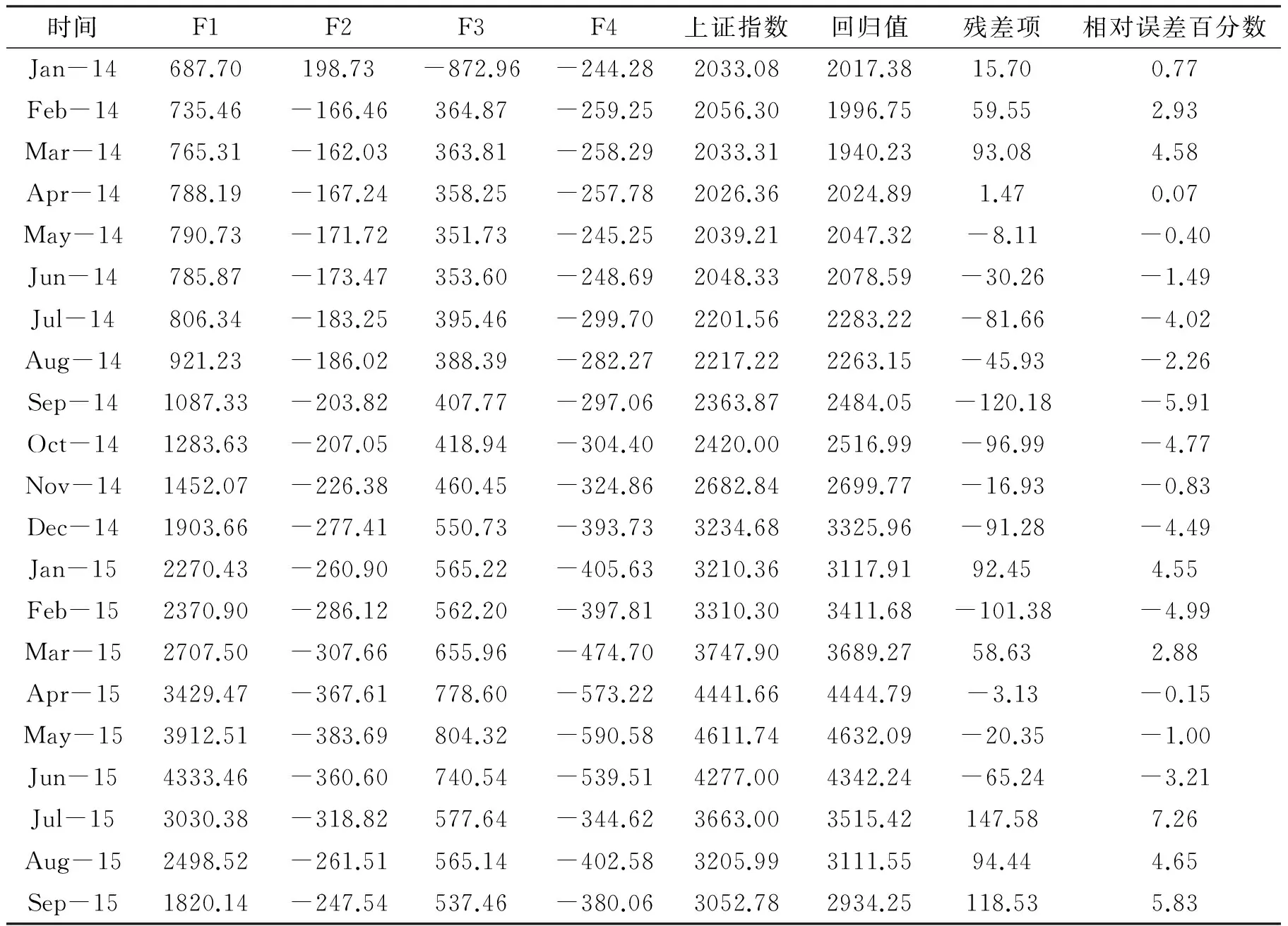
表2　2014年1月至2015年9月主成分综合变量多元线性模型回归值和上证指数的对比

从上表回归模型和实际上证指数误差数据可以看出，建立在主成分分析基础上的上证指数多元线性回归关联式，消除了原始变量之间的多重共线性，无论是回归系数还是回归方程均为显著，复相关系数也表明方程的拟合度高，总体显著性好。2014年1月至2015年9月的模型回归值与上证指数实际值的误差除了2015年7月以外，均在6%之下，可以作为上证指数变化的参考依据，用以作为股票投资的基本判断。

因为回归模型不能及时体现离散事件的短期影响，当期相对误差会明显加大。以2015年7月为例，当期遭遇了A股上市公司大面积停牌， 至7月8日收盘，两市共1312只股票停盘，占A股市场的47.2%。同时，监管层救市政策出台，中央汇金入市操作等事件的合力冲击造成7月的模型回归值相对误差达到7.26%。故在借鉴回归模型的参考指导外，还需高度关注政策(如本次的降杠杆，去除场外配资的政策)引发的冲击事件对股市造成的影响。

2　总结

股票作为一个金融产品，其影响因素是多方面的。本文通过对股市上呈现的数据进行挖掘，利用统计方法从宏观经济指标方面分析了对上证指数的影响。在常见宏观经济指标中,选取了对上证指数有明显影响作用的指标，通过主成分分析消除了各原始因素之间的多重共线性，建立了以主成分综合变量为自变量，上证指数为因变量的多元线性回归关联式。借助于上述所得的模型和结论，可以为个人在规避市场系统风险提供一个参考依据，从而降低市场系统性风险对个人股票投资带来的损失及提高本金收益率。

参 考 文 献

[1]傅德印.Excel 与多元统计分析-附实用计算机程序[M].北京：中国统计出版社，2007

[2]左媛.上市公司盈利质量分析[J].安徽冶金科技职业学院学报，2012，1

收稿日期：2016-01-22

作者简介：胡人友(1997-)，男，马鞍山市中加双语学校。

中图分类号：F830.91

文献标识码：B

文章编号：1672-9994(2016)01-0076-04

Analysis of Influence Factors of the Shanghai Composite Index

HU Ren-you

Abstract：Though multivariate statistical analysis, the national economic factors which influence The Shanghai Composite Index are analyzed. The multivariate linear model is deduced. Focusing on the error between calculated value and actual one, the conclusion is drawn that the policy event as instant impact force has the great influence on the Index. So, when using the model as guide for stock investment,the policy event should be paid high attention.

Key words：The Shanghai Composite Index；data digging factor analysis；principal components analysis；multivariate statistical analysis