海洋盐度分布的插值方法应用与对比研究

王兴，刘莹，王春晖，李保磊，钟山（1.国家海洋局北海环境监测中心，山东　青岛　266033；2.山东省海洋生态环境与防灾减灾重点实验室，山东　青岛　266061；3.国家海洋局海洋溢油鉴别与损害评估技术重点实验室，山东　青岛　266033；.国家海洋局北海预报中心，山东　青岛　266061）

海洋盐度分布的插值方法应用与对比研究

王兴1，2，3，刘莹1，3，王春晖1，2，3，李保磊1，3，钟山4
（1.国家海洋局北海环境监测中心，山东青岛266033；2.山东省海洋生态环境与防灾减灾重点实验室，山东青岛266061；3.国家海洋局海洋溢油鉴别与损害评估技术重点实验室，山东青岛266033；4.国家海洋局北海预报中心，山东青岛266061）

空间插值在海洋环境评价中有着广泛的应用，常用的插值方法有：线性插值、最近邻点插值、自然邻点插值、三次多项式插值、反距离权重插值、克里金插值等。盐度是海水重要的环境因子，基于2012年8月份的北海区盐度监测数据，采用空间插值分析表层盐度分布，并通过开展不同插值方法的插值实验，对插值结果进行曲面分析和误差分析，对比各插值方法的特点与适用性。结果显示：基于本次海洋环境监测的站位与盐度数据，克里金插值、自然邻点插值曲面趋势符合较好，而且相对其他插值方法误差也较小，是相对适用于海水盐度的空间插值方法。

盐度；插值方法；误差分析；克里金；自然邻点

盐度作为反映河口、海湾、近海生态系统健康程度的重要环境因子，对海洋环境与生态影响深远（曹伏君等，2010；张洪亮等，2006；肖纯超等，2012）。因此在海洋环境监测与评价中，盐度是必不可少的一项监测要素。海水盐度在空间上是连续分布的，但由于监测人力、物力、时间等因素，实际得到的监测值往往比较稀疏；为获取区域性相对完整的数据，从而对该区域的整体特征进行分析，需要采用空间插值的方法，即利用已知点的数值来估算其他点的数值。

空间插值在海洋环境评价中有着重要而广泛的应用：评价报告中海洋环境要素等值线分布趋势图的绘制，海洋环境公报中污染面积的确定（付瑞全等，2014），都是在监测站位实测值的基础上，选用一种空间插值方法计算得到研究区域的网格场数据，再进一步绘图、计算、分析得到评价结论。不同插值方法的特点与适用性比较，在气象领域已做了大量研究 （Andreas et al，1995；Dirks et al，1998；范银贵等，2002；杜红娟等，2012），而在海洋领域研究成果还较少；本文拟通过分别采用不同的空间插值方法，对比实测盐度水平分布的插值效果，分析不同插值方法的特点与适用性。

1　方法与材料

1.1插值方法介绍

空间插值方法可以分为几何方法、统计方法、空间统计方法、函数方法、随机模拟方法、物理模型模拟方法和综合方法等（李新等，2000；），各种插值方法有数百种之多（Jin et al，2014；孙然好等，2010）。这里简要介绍环境科学领域中比较常用的六种插值方法：线性插值、最近邻点插值、自然邻点插值、三次多项式插值、反距离权重插值、克里金插值。

（1）线性插值（Linear）

线性插值又叫线性三角网插值，线性三角网法是最佳的Delaunay三角形，将连接数据点间的连线形成三角形，所有三角形的边都不能与另外的三角形相交，构成一张由三角形拼接起来的覆盖网格范围的网（陈欢欢等，2007）。该方法将在整个研究区域内均匀分配数据，地图上的稀疏区域会形成截然不同的三角面，每一个三角形定义了一个覆盖该三角形内格网结点的面（范银贵，2002）。

（2）最近邻点插值（Nearest Neighbor）

最近邻点插值又叫泰森多边形方法，最初用于平均降水量的计算，目前在GIS和地理分析中较常用（冯仲科等，2006）。该插值方法认为空间中两点之间的距离越近，这两点的属性值差异就越小，因此就可以用距离未知点最近的已知值来对未知点的数值做出估计（李峋等，2009）。用泰森多边形方法得到的结果图变化只发生在边界上，在边界内都是均质的和无变化的。

其数学表达式为：

其中：ve表示待插点变量值，vi表示第i个已知点的变量值。i点必须满足如下条件：

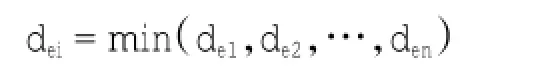
其中：dei表示待插点与第i个已知点间的距离。

（3）自然邻点插值（Natural Neighbor）

自然邻点法又叫双次泰森多边形法，是基于泰森多边形法基础上，进一步建立待求点周围的二次Voronoi结构图，用面积权重计算待估点的值（杜红娟等，2012）。

其数学表达式为：

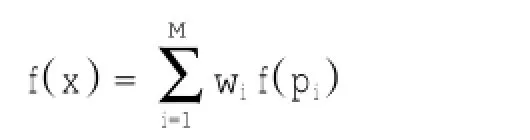
其中，f（x）是待插x点处的插值结果，M为自然邻点的个数，f（pi）是自然邻点pi处的值，wi代表自然邻点pi所占的权重系数（张伟等，2011）。

（4）三次多项式插值（CubicPolynomial）

多项式插值是常用的方法之一，文中采用的为三次多项式插值（陈欢欢等，2007），其多项式形式为：

（5）反距离权重插值（Inverse Distance Weight）

反距离权重法是一种以待插点与观测已知点之间距离为权重的插值方法，离待插点越近的已知点赋予的权重越大（朱求安等，2004）。

其数学表达式为：

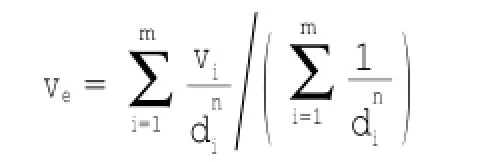
其中，ve为待插点的估算值，vi是第i个已知点的变量值，di是第i个已知点与待插点之间的距离；m为参与计算的已知点个数；n为幂指数，它控制着权重系数随待插点与样本点之间距离的增加而下降的程度。

当n=0时，所有参与计算的样本点权重相等，均为1/m，该方法变为算术平均值法；当n=1时，称为距离反比法，是一种常用而简便的空间插值方法；当n=2时，称为距离平方反比法，是最常使用的方法；当n取值很大，接近于正无穷时，待插点的估算值等于离待插点最近的样本点的值，该方法变为最近邻点法。

（6）克里金插值（Kriging）

克里金插值，又称克里格法，是法国G.马特隆教授以南非矿山地质工程师D.G.Krige的名字命名的一种方

法（王仁铎等，1988）。该方法首先考虑空间属性在空间位置上的变异分布，确定对一个待插点值有影响的距离范围，然后用此范围内的已知点来估计待插点的属性值。

其数学表达式为以下两个方程组成的方程组：

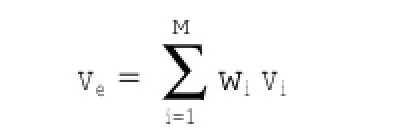
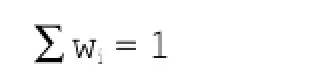
其中，ve为待插点的估算值，vi是第i个已知点的变量值，m为参与计算的已知点个数，wi是第i个已知点的权重系数。

权重wi的选择必须保证ve无偏估计，且估计的方差σ2e小于观测值的其它线性组合产生的方差。

1.2监测数据与实验设计

监测数据采用2012年8月份国家海洋局北海环境监测中心在北海区的水质监测资料（图1），共88个站位，插值分析数据采用表层盐度监测值。

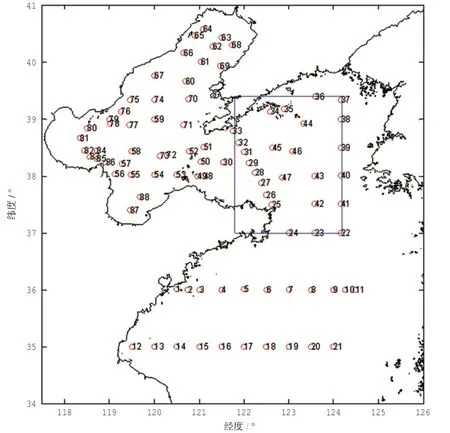
图1　盐度监测站位

插值曲面分析：选取站位分布较密集的区域作为插值实验范围（图1中蓝框内）：121.8°-124.2°E，37.0°-39.4°N，网格分辨率为0.05度；分析曲面是否平滑美观，以及变化趋势的符合性。

插值误差分析：在选定的北黄海范围内随机选择1个站点，去掉该站点的盐度数据，再用剩余87个站的盐度数据根据不同的空间插值方法分别插值计算出该点的值，与实际的监测值相比较。本次插值实验随机选取了5个监测站，分别为27、35、38、42、46号站。

2　结果与讨论

2.1插值曲面

图2-图7是根据2012年8月盐度监测结果在实验范围内分别采用线性插值、最近邻点插值、自然邻点插值、三次多项式插值、反距离权重插值、克里金插值等常用空间插值方法得到的插值曲面图。根据这些盐度插值曲面图，分析各插值方法的特点，比较各曲面的美观性和趋势符合性。

（1）线性插值

线性插值又叫三角网法，该插值方法与手工绘制等值线相近。监测站数据（图中蓝圈）被用来定义各个三角形，所以监测数据在插值曲面上符合性较好，插值结果落在最大值与最小值之间。盐度的插值曲面（图2）总体趋势符合，但高值区或低值区存在明显棱角、折线，插值曲面平滑性欠佳。

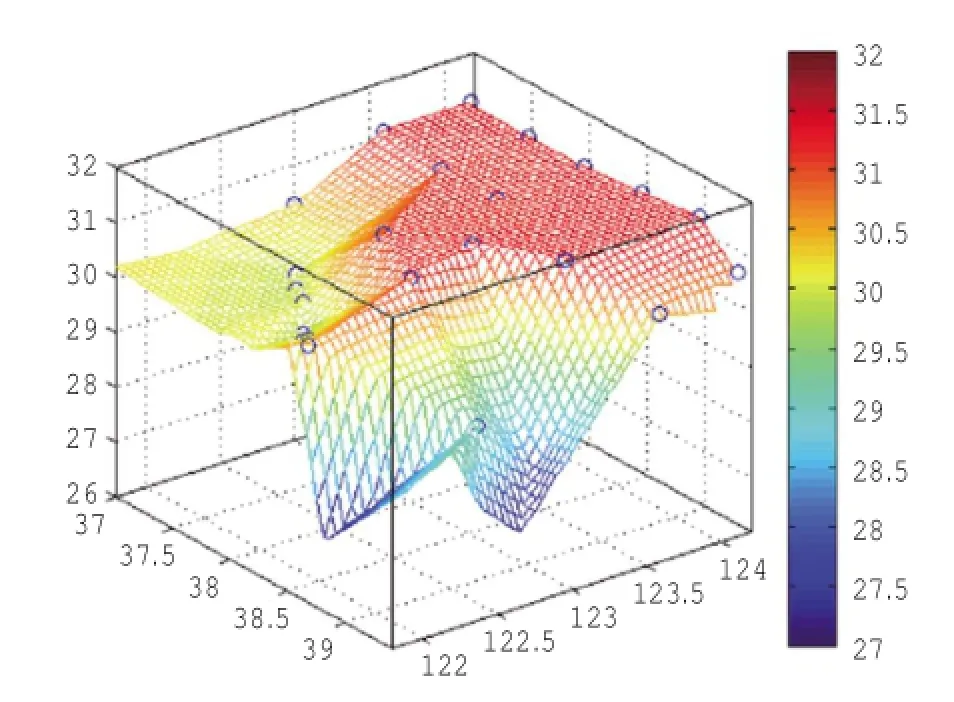
图2　线性插值

（2）最近邻点插值

最近邻点插值方法是取距离插值点最近的站点监测值，该方法优点是不需要其它前提条件，方法简单，计算效率高，缺点是受已知点的影响较大，只考虑距离因素，对其它空间因素和变量所固有的某些规律没有考虑。盐度的插值曲面（图3）产生多片台地区块，曲面不连贯，美观性差，也不符合海水中盐度的分布趋势。

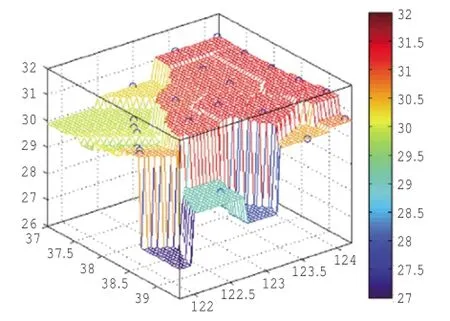
图3　最近邻点插值

（3）自然邻点插值

自然邻点插值，插值后的物理场数据可以产生更为光滑、精度更高的可视化图形（高洋等，2005）。盐度的插值曲面（图4）连续、平滑，趋势符合性较好，没有明显的缺点。

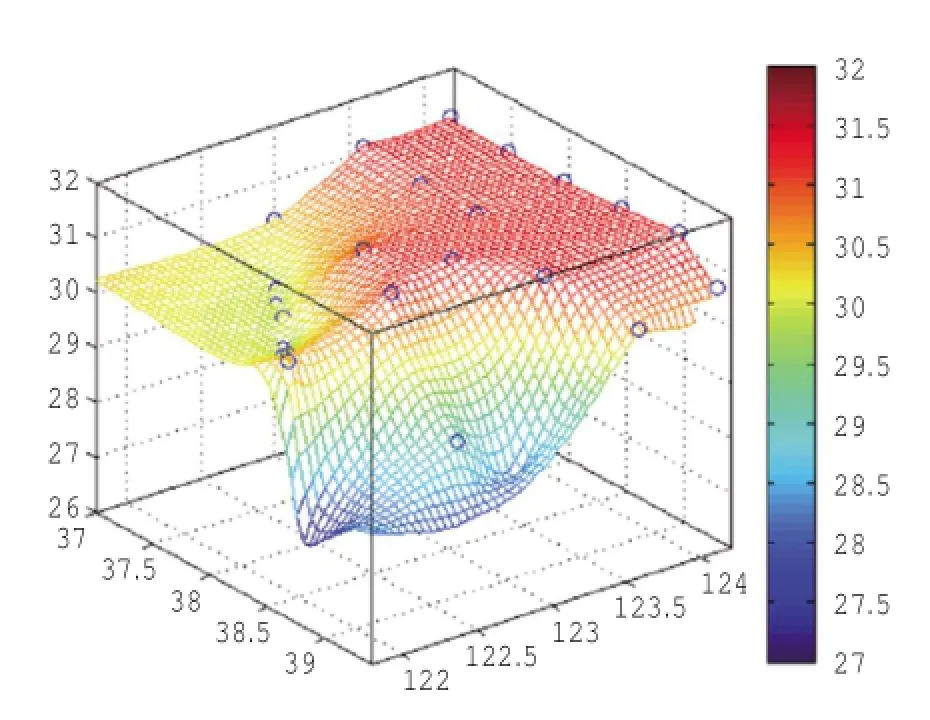
图4　自然邻点插值

（4）三次多项式插值

三次多项式插值，具有较平滑的曲面，盐度的插值曲面（图5）趋势符合性较好，但在插值区东北部边缘存在“毛刺”，局部欠佳，总体较好。

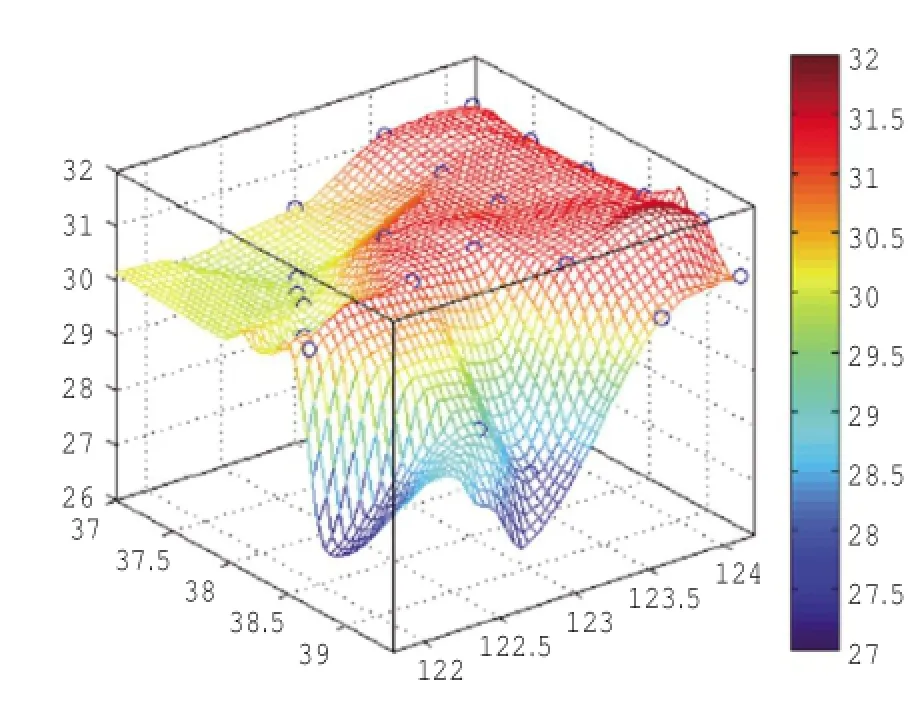
图5　三次多项式插值

（5）反距离权重插值

反距离权重插值，离待插点越近的已知点赋予的权重越大，本次实验中采用权重贡献与距离的平方成反比。形成的插值曲面（图6）所有数值都在监测值的最大值、最小值之间，曲面连续性较好，但当待插值点附近的监测数据值很大或很小时，待插点的结果容易受到极值点的影响而产生明显的“牛眼”现象。

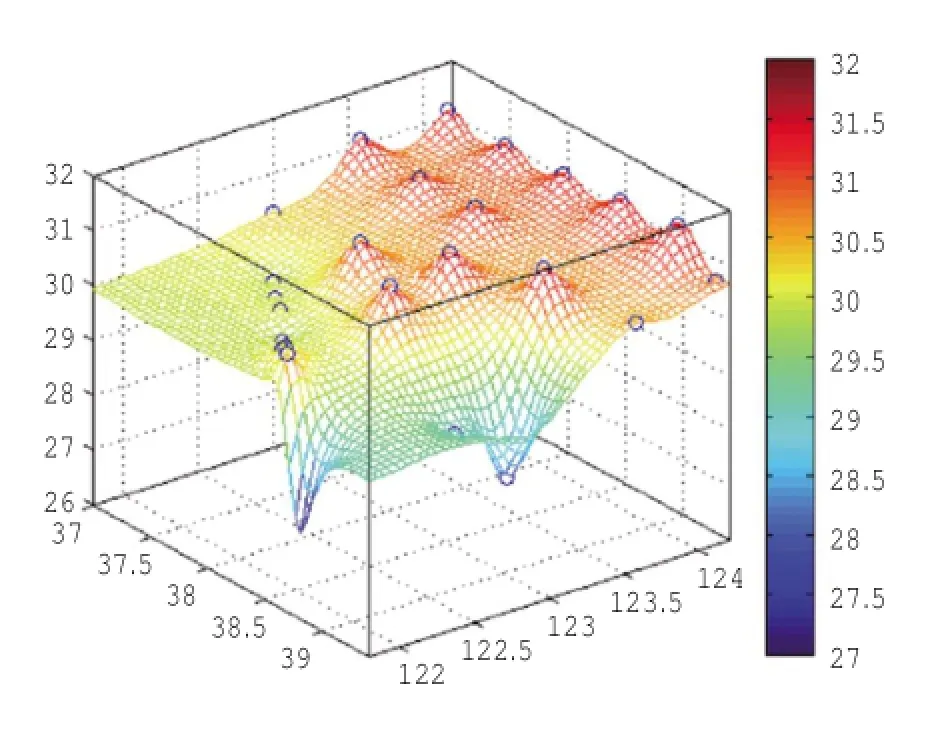
图6　反距离权重插值

（6）克里金插值

克里金插值，与反距离权重插值仅考虑距待插点的距离不同，克里金插值不仅考虑距待插点的距离，还要综合考量各监测点的空间分布和排列，考虑变量的空间相关性（刘春洋等，2012）。盐度的插值曲面（图7）光滑连续，趋势符合性较好，没有明显的缺点。

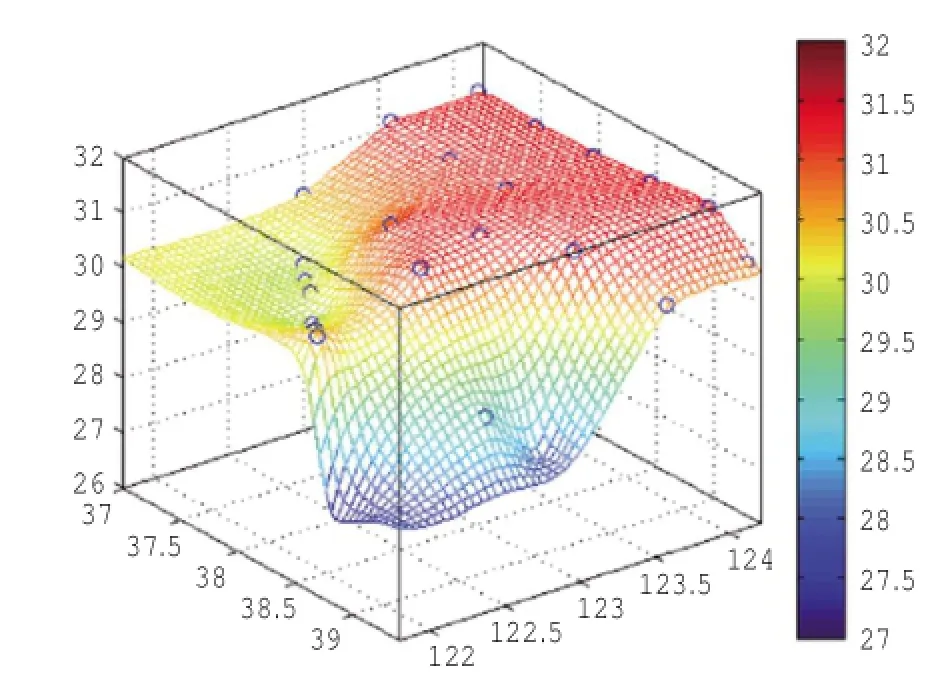
图7　克里金插值

2.2插值误差

（1）绝对误差（图8）

盐度插值绝对误差：27号站总体插值误差较好，采用不同的插值方法误差变化较小，其中采用反距离权重、克里金方法误差较小，采用最近邻点方法误差最大；35号站总体误差较大，推测可能与该站周围分布着大量岛屿有关，相对采用最近邻点、三次多项式方法误差较小，采用反距离权重方法误差最大；38号站采用克里金、线性方法误差较小，采用反距离权重方法误差最大；42号站采用最近邻点、自然邻点方法误差较小，采用反距离权重方法误差最大；46号站采用克里金、线性方法误差较小，采用反距离权重方法误差最大。5个站平均误差，克里金和最近邻点方法较小，反距离权重方法最大。

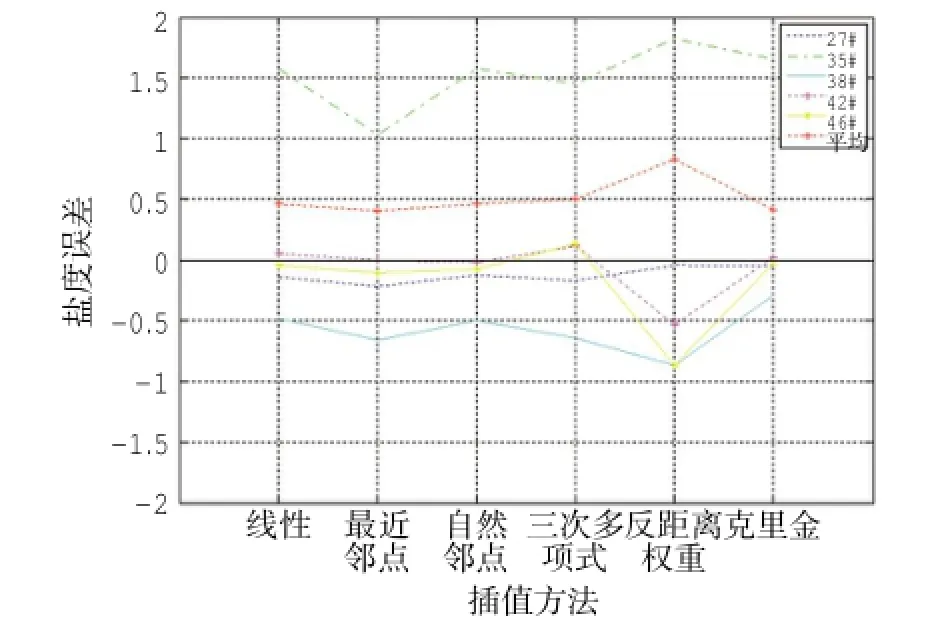
图8　插值方法误差对比

（2）相对误差（图9）

盐度插值相对误差：27号站采用各种插值方法相对误差都小于1%，采用最近邻点方法相对误差较大；35号站插值相对误差都大于3%，采用最近邻点、三次多项式方法误差较小，采用反距离权重方法误差最大；38号站采用克里金、线性方法误差较小，采用反距离权重方法误差最大；42号站采用反距离权重方法误差最大，而采用其它插值方法相对误差都很小（小于0.5%）；46号站同42号站类似，除反距离权重插值外，其它插值方法相对都很小。5个站平均相对误差，最近邻点和克里金方法较小，反距离权重方法最大。

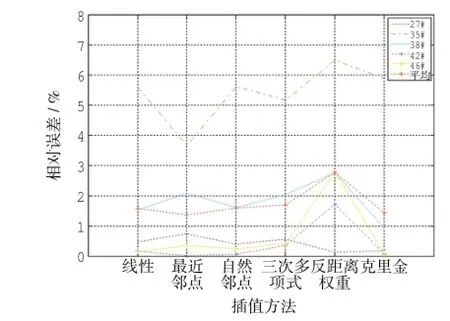
图9　插值方法相对误差对比

（3）标准误差（图10）

盐度插值标准误差：反距离权重插值误差最大，最近邻点插值最小，其它插值方法标准误差值较接近。

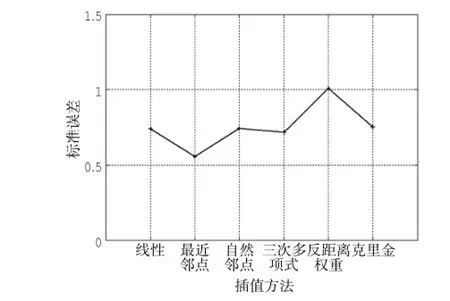
图10　插值方法标准误差对比

3　结论

根据各插值曲面的特点（表1）分析，克里金插值和自然邻点插值美观性和趋势符合性最好，三次多项式插值和线性插值总体较好。

各插值方法的误差（表2）分析显示：几种常用插值方法的盐度插值平均误差都大于0.4，插值计算引入了较大的误差；相对而言，最近邻点插值和克里金插值最好，自然邻点插值和线性插值总体较好。

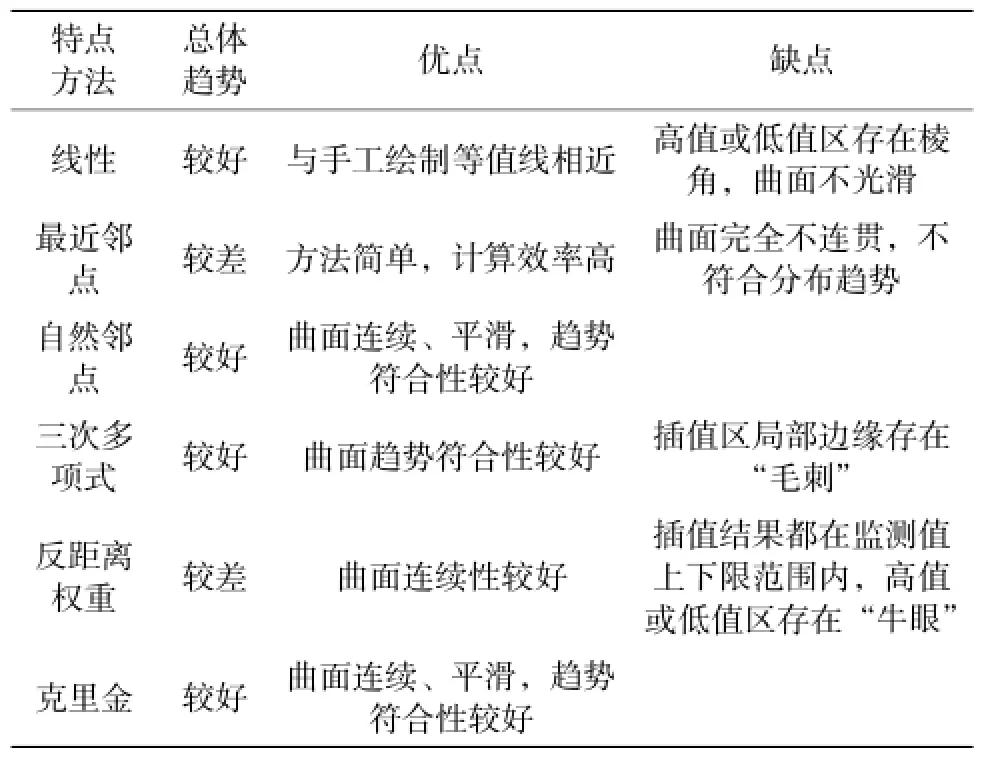
表1　插值方法曲面分析特点统计

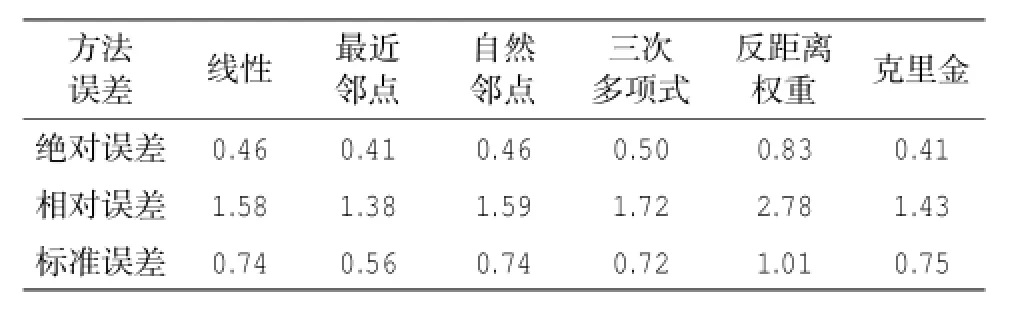
表2 插值方法平均误差统计

基于本次盐度监测数据，综合插值曲面分析和误差分析结果：海水盐度平面分布最适宜采用的插值方法为克里金插值，自然邻点插值也较为适宜。

同时，无论采用哪种空间插值方法，都会引入较大的误差，在监测条件允许的情况下，适度加密监测站位是必要的，尤其是在插值误差较大的区域。

Andreas S,Gerhard W,Petra S,et al,1995.Interpolation errors in wind fields as a function of spatial and temporal resolution and their impact on different types of kinematic trajectories.Journal of Applied Meteorology,34:2149-2165.

Dirks K N,Hay J E,Stow C D,et al,1998.High-resolution studies of rainfall on Norfolk Island part II:interpolation of rainfall data.Journal of Hydrology,208:187-193.

Erxleben J,Elder K,Davis R,2002.Comparison of spatial interpolation methods for estimating snow distribution in the Colorado Rocky Mountains.Hydrological Processes,16:3627-3649.

JinL,Andrew D H,2014.Spatial interpolation methods applied in the environmental sciences:A review.Environmental Modelling&Software,53:173-189.

Vicente Serrano S M,Saz Sánchez M A,Cuadrat J M,2003.Comparative analysis of interpolation methods in the middle Ebro Valley （Spain）:application to annual precipitation and temperature.Climate Research,24:161-180.

曹伏君，刘志刚，罗正杰，2010.文蛤稚贝盐度适应性的研究.海洋通报，29（2）：156-160.

陈欢欢，李星，丁秀文，2007.Surfer8.0等值线绘制中的十二种插值方法.工程地球物理学报，4（1）：52-57.

范银贵，2002.空间插值方法在绘制降水量等值线中的应用.水利水电科技进展，22（3）：48-50.

付瑞全，向先全，杨翼，等.基于WEB服务的海水污染面积计算方法研究.海洋通报，2014，33（6）：712-716

高洋，张健，2005.基于自然邻点插值的数据处理方法.中国科学院研究生院学报，22（3）：346-351.

李新，程国栋，卢玲，2000.空间内插方法比较.地球科学进展，15 （3）：260-265.

李峋，仵彦卿，范海梅，2009.高维空间插值在海洋环境数据预处理中的应用.海洋环境科学，28（6）：729-733.

刘春洋，李轶平，董婧，2012.基于GIS的海洋底栖生物栖息密度空间插值方法.海洋环境科学，31（3）：443-447.

杜红娟，刘九夫，谢自银，等，2012.基于网格划分的自然邻点法在降雨空间分布研究中的应用.水利水电技术，43（4）：23-25.

冯仲科，郭清文，朱萍，2006.Voronoi图—泰森多边形法在角规测树中的应用.林业资源管理，（3）：44-47.

唐保军，尹飞，归从时，2012.海水盐度对紫血蛤耗氧率和排氨率的影响.台湾海峡，31（1）：89-94.

孙然好，刘清丽，陈利顶，2010.基于地统计学方法的降水空间插值研究.水文，30（1）：14-17.

王茂林，李岑，杨敏，等，2014.盐度对仿刺参存活和NaKATP酶活性的影响.渔业现代化，41（1）：6-9.

王仁铎，胡光道，1988.线性地质统计学.北京，地质出版社，4-10.

王维奇，王纯，刘白贵，2012.盐度对湿地枯落物分解过程中碳氮磷化学计量比的影响.中国环境科学，32（9）：1 683-1 687.

肖纯超，张龙军，杨建强，2012.2004—2009年黄河口近岸海域低盐区面积的变化趋势研究.中国海洋大学学报，42（6）：40-46.

张洪亮，杨建强，崔文林，2006.莱州湾盐度变化现状及其对海洋环境与生态的影响.海洋环境科学，25（增刊1）：11-14.

张伟，李纯厚，贾晓平，等.底栖生物生物量空间插值方法研究.海洋通报，2010，29（3）：351-356.

张伟，覃庆炎，简兴祥，2011.自然邻点插值算法及其在二维不规则数据网格化中的应用.物探化探计算技术，33（3）：291-295.

朱求安，张万昌，余钧辉，2004.基于GIS的空间插值方法研究.江西师范大学学报，28（2）：183-188.

庄平，贾小燕，冯广鹏，等，2012.盐度对中华绒螯蟹雌性亲蟹代谢的影响.中国水产科学，19（2）：217-222.

（本文编辑：岳心阳）

Study on the application and comparison of interpolation methods for the marine salinity distribution

WANG Xing1,2,3,LIU Ying1,3,WANG Chun-hui1,2,3,LI Bao-lei1,3,ZHONG Shan4
（1.North China Sea Environmental Monitoring Center,Qingdao 266033，China；2.Shandong Provincial Key Laboratory of Marine Ecology and Environment&Disaster Prevention and Mitigation,Qingdao 266061，China；3.Laboratory of Marine Spill Oil Identification and Damage Assessment Technology,Qingdao 266033，China；4.North China Sea Marine Forecasting Center,Qingdao 266061，China）

Spatial interpolation is widely used in the marine environment assessment.The commonly used interpolation methods include Linear,Nearest Neighbor,Natural Neighbor,Cubic Polynomial,Inverse Distance Weight and Kriging interpolation methods.Salinity is an important marine environmental factor.Based on the salinity data of North China Sea in 2012 August,the surface salinity distribution is analyzed by those interpolation methods,and different interpolation experiments are designed.And the characteristics and applicability of each interpolation methods are compared by the trend surface analysis and error analysis.The results show that the Kriging interpolation and the Natural Neighbor interpolation have better trends and less error,and they are suitable interpolation methods for the marine salinity distribution,comparing with other interpolation methods.

salinity;interpolation method;error analysis;Kriging;Natural Neighbor

刘莹，电子邮箱：liuying@bhfj.gov.cn。

P76

A

1001-6932（2016）03-0324-07

10.11840/j.issn.1001-6392.2016.03.011

2015-05-27；

2015-06-21

山东省海洋生态环境与防灾减灾重点实验室2012年度开放基金资助项目（2012001）。

王兴（1983-），男，学士，高级工程师，主要从事物理海洋、海洋生态环境研究。电子邮箱：sino1983@sina.com。