一种实用海洋浮标数据异常值质控方法
2016-08-15刘首华陈满春董明媚高志刚张建立武双全林峰竹国家海洋信息中心天津300171
刘首华,陈满春,董明媚,高志刚,张建立,武双全,林峰竹(国家海洋信息中心,天津 300171)
一种实用海洋浮标数据异常值质控方法
刘首华,陈满春,董明媚,高志刚,张建立,武双全,林峰竹
(国家海洋信息中心,天津300171)
针对海洋浮标的波高观测数据,通过结合格拉布斯准则(Grubbs)、局地异常值检验方法和波高观测误差控制建立了一种实用的数据异常值质控方法并对波高观测异常值进行了质控效果检验。结果表明,该质控方法由于加入了波高观测误差控制,从而避免了将大量正常数据误判为异常数据,异常数据判断的准确率达到了较高水准。另外该方法也可以作为一种实用质控方法推广使用于其他海洋浮标观测要素。
海洋浮标;异常值;质量控制;格拉布斯准则
我国沿海海域布放了众多海洋观测浮标,观测要素包含了海风、海浪、海流、温度、盐度等重要的水文气象参数。为完成观测数据的实用化使用,需要对海量观测数据进行严谨而科学的质量控制(质控)。数据质控不仅能剔除数据序列中不正确的数据,也能从不正确数据中推测观测浮标的情况,便于对观测浮标进行及时的检查和维修。海洋浮标数据常用的质控内容包含时间质控、位置质控、范围质控、异常值质控、数据漂移性质控、梯度质控等(National Data Buoy Center,2009)。数据质控的核心主体是观测数据序列中的异常值质控。超出仪器观测范围的值可以通过范围控制进行剔除,而对在仪器测量范围内但又明显脱离相邻数据统计特征的数据需要异常值质控剔除。
数据序列中异常值的检测普遍存在于科学研究的各个领域,其抽象为离群数据的搜索和聚类,常见于数学领域和信息科学领域。关于时间序列异常值的判定,具有较为庞杂的方法分类(黄谟涛等,1999;Hodge et al,2004;李光强,2009),但比较常用且具有共性特征的是基于经典统计理论的离群点检测方法(王占全,2005)。基本思想是假定已知数据集满足某种统计分布,通过分析数据点偏离正常统计分布的程度判定数据点是否异常或离群。基于统计理论的异常值检测方法能够对多个数据点中的单个异常点做出比较准确的判断。异常值的出现方式是比较复杂的,经常以连续多个方式或以斑块方式出现,在局部时间段内甚至超过正常数据的数量。在这种情形下,基于统计理论的异常值检测方法就难以对这些异常值做出有效的判断。
对很多时间序列观测数据而言,有些观测值在统计方法上判定为异常值,但是这些异常值可能没有超过仪器本身的观测误差,因此这时候判断的异常值应理解为误判。不同类型的观测数据,其异常值都有不同外观特征及性质,并不存在一种普适性的异常值检测方法。因此要针对具体的数据给出具体的质控方法。虽然在海洋数据质控方面存在大量研究成果,但内容主要围绕质控共性理论方法的探讨(于婷等,2013;郑琳等,2014),鲜见针对浮标数据的具有可行性的数据质控方法流程。本文针对浮标观测数据,通过结合统计检测方法、局地检测方法和浮标仪器本身观测误差控制,提出了一种实用的浮标数据质控方法及具体流程,并对结果进行了分析。
1 方法介绍
浮标数据为时间序列性观测数据,误差来源较为复杂,针对数据序列本身从3个方面对其进行质控。一是基于统计理论的Grubbs准则;二是局地异常值检验法;三是浮标仪器观测误差的控制。
1.1Grubbs准则介绍
常用的异常值统计判别准则有莱以特准则(3σ准则)、罗曼诺夫斯基准则、奈尔准则、格拉布斯(Grubbs)准则、狄克逊(Dixon)准则等(杨筱,2009)。各个方法的基本原理大同小异,但不同情形下采用的准则有所不同。Grubbs准则是常用的异常值检测方法。基本思路是根据两个参数(观测值与均值的距离、数据序列的标准差)来判断观测值脱离数据序列程度。由于其研究对象可以为少量数据,而且不同的数据量具有不同的临界值参数(异常值判定标准),相比固定判定标准的莱以特准则,Grubbs准则在有限数据量判定上更具有理论上的合理性。因此我们选定该方法作为浮标数据质控方法。
假定浮标观测数据序列为x1,x2,……,xn,数据序列的均值为。选取其中距离最大的数据xi。则可给出如下理论表达式(Grubbs,1950;国家质量技术监督局,1998;史静涛等,2011):
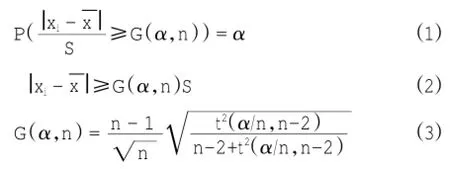
其中S为数据序列的标准差,α为显著性水平,n为数据序列的个数。G(α,n)为格拉布斯临界值,可以通过查阅Grubbs临界值表或根据(3)式得到。(3)式中t为自由度为n-2,显著性水平为α/n的单边界检验t分布的临界值。测量值是否异常可以通过公式(2)进行判定。
1.2局地检测方法
统计性的异常数据检测方法一般具有普适性,应用范围比较广泛,但其作为一种统计方法,需要在满足一定数据量前提下,才具有稳定性和准确性。Grubbs准则在数据量较少情况下难以进行异常值的判定。基于此,引入了局地异常值检测方法。它主要以几个数据之间的比较为基础,具有较大的偶然性,但是具有较为直观的判断标准,能够检测大多数尖峰异常值。参考了欧洲SeaDataNet组织采用的异常值检测方法(SeaDataNet,2010)。观测数据xn的前后数据分别为xn-1和xn+1,则xn是否异常可用如下公式来进行判断。
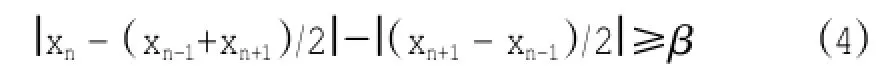
其中β是临界值系数,可以根据不同的观测要素特点进行设置。该方法具有比较直观的特点,其隐含假定xn-1和xn+1均为正常数据,通过公式(4)比较认定异常数据。如果xn-1和xn+1中存在异常数据,则xn就会出现误判,这也是局地检测方法的一个缺点。
1.3浮标观测误差控制
对浮标测量范围内数据,结合统计性的Grubbs准则和局地异常数据检测方法对数据进行整体和局部的质控。假定浮标观测数据具有1位小数,在海况较为稳定的情况下就可能出现一段时间较多数据相同的情况。如果在相同的一段数据中存在一个不同值,不同值与其他数据的差值为0.1。根据Grubbs准则,这个差异数据的统计特征会明显区别于其他数据,极有可能会被认定为异常值。由于浮标本身存在观测误差,如波高的观测误差标准一般为±(0.3m+0.1H) (H为波高) (国家海洋局,2011 a,2011 b),因此波高差值在0.1m时,远低于自身观测误差,显然不能认定为异常值。针对浮标本身的误差情况,为防止出现过于明显的误判,加入了浮标误差值的控制。
1.4浮标有效波高数据质控算法
以浮标观测有效波高数据为例,以上面介绍的方法为基础,介绍浮标有效波高数据的具体质控流程。假定在一段时间内的海洋有效波高要素观测值集合为Uoriginal:

在针对浮标数据的质控中,首先需要排除浮标测量范围外的数据。不同浮标的有效波高观测范围有所不同,取浮标有效波高标称范围值为 [0 25]。进行质控的条件有如下3个:
1)统计性质控条件—Grubbs准则。公式(2)中显著性水平α取0.05时会导致一些正常数据误判为异常值。为尽量保留正常值,减少误判的产生,通过大量实验得出公式(2)中显著性水平α 取0.01时会得到相对满意的结果。数据的统计特征依赖于统计样本的多少,不同样本数量对异常值的判定是不同的。尤其是斑块型异常值(短时间内出现的大量异常值),需要在更长时间尺度对其进行统计特征检验。基于此,采用多个尺度对异常值进行质控,对于(2)中n的长度通过如下方式选取:
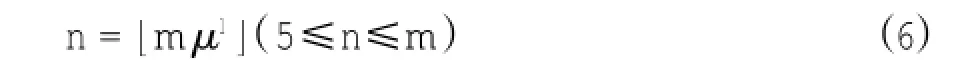
其中m为总检测数据的个数,μ为经验比例系数,本研究取值0.618。n为向0取整的自然数,l为符合n值范围条件的0和自然数。例如检测数据个数为1 000,则n分别取 [1 000,618,381,236,145,90,55,34,21,13,8,5],即首先以1 000个数据为一组进行异常值检测,在遍历完所有观测数据后,对检测的异常值进行剔除。对剩余的数据再以618个为一个组进行异常值检测,对检测的异常值进行剔除后再对剩余的数据以381个为一组按照以上方式进行异常值检测,以此类推,最终形成正常数据集U1。
2)对于集合U1,采取局地奇异值检测方法,见公式(4)。系数β是依赖于观测要素的经验性参数,不同观测要素需要对应不同的数值,而且不同值会产生不同结果,通过大量对比实验得出了较为满意的参数值,本文β取值为1.1。检测完成后形成正常数据集合U2。
3)对于异常值数据集合Uoriginal-U2,对每个异常值进行检测,如果异常值与相邻正常值的差值不超过浮标观测误差,则认为该异常值为正常值。假定异常值及相邻数据分别为xn-1,yn,xn+1,其中yn为异常值。x值为相邻正常值或异常值。如果x值中存在正常值,那么判定yn是否为正常值采用下式(7)进行判定,如果x值中不存在正常值,则yn判定为异常值。对于误判为异常值的数据形成集合U3。
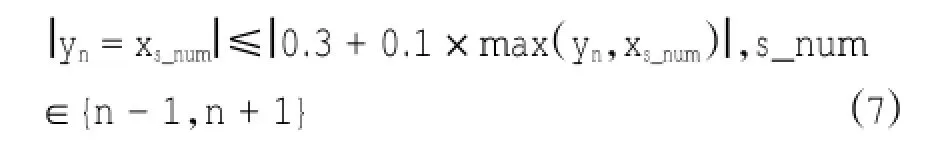
综上最终形成异常值集合为Uoriginal-U2-U3,正常值集合为U2+U3。
2 质控结果讨论与分析
选择国家海洋局QF104和QF201浮标连续的有效波高观测数据进行质控分析。QF104浮标数据连续性较好,能够代表一部分浮标观测情况。QF201浮标观测连续性相对较差,存在大量斑块型异常值,也能够代表一部分浮标的观测情况。数据及质控情况见表1,图1,图3。
进行检验的两个浮标QF104和QF201的数据量分别为97 519个、4 410个。范围控制 [0 25]排除的数据量分别为5 834个、33个,占总数据量比例为5.98%,0.75%。在排除浮标观测范围外数据后,通过人工检查,发现异常值数量分别为11个和117个,在此作为两个浮标异常值准确可靠的个数。
采用多种不同的方式对异常数据进行检测。如果只采用Grubbs准则进行检测(表1,Grubbs准则检测),QF104和QF201异常数据数量分别判定为314个和360个,远大于准确异常值数量,错判个数分别为303个和254个。图1(b)和图3(b)显示判定的异常值出现在整个时间序列中,与真实异常值(图1(a)和图3(a))有较大差别。经分析发现,在一串连续数字中,如果一个数字与其他数字存在一定的统计差别,这个数字在数学上认定为异于其他数据,容易判定为异常数据。如图2(b),第23 103个数据在统计上异于邻近数据,在数学上判定为异常数据。对于浮标波浪观测来说,其波高误差范围一般大于0.3 m(国家海洋局,2011 a,2011 b),因此这种数学判定依据对于浮标观测数据过于严格,该数据与邻近数据相差仅0.1 m,应判定为正常数据。因此异常数据检测方法中加入观测误差控制是必要的。
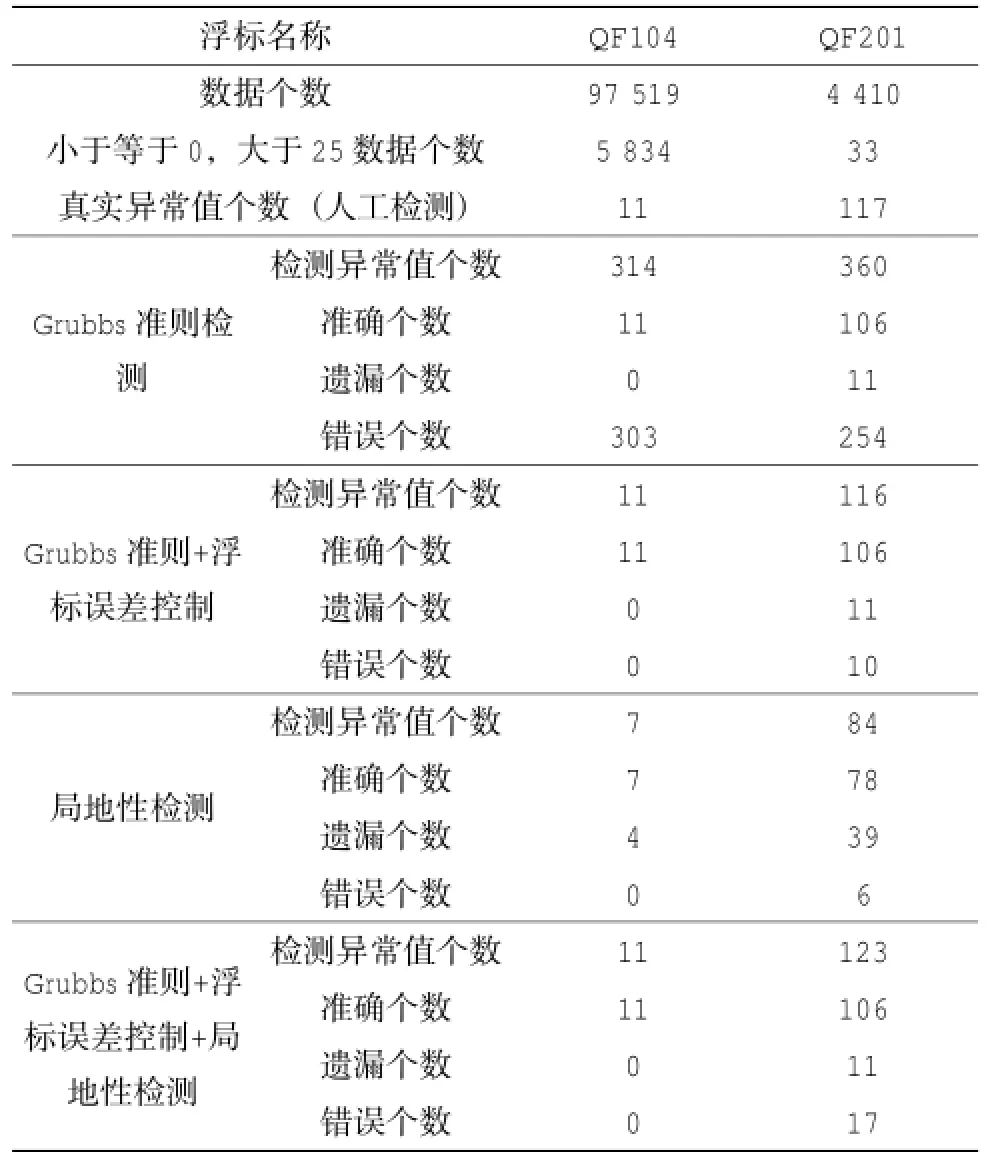
表1 浮标有效波高数据质控情况

图1 QF104浮标有效波高数据整体质控情况(a)蓝星号为原始数据,红星号为真实异常数据,红框号为经Grubbs准则和误差控制检测的异常数据,绿圈为局地方法检测的异常数据;(b)红钻石为Grubbs准则检测的异常数据
在加入浮标误差控制后(表1,Grubbs准则+浮标误差控制),QF104异常值误判数量由303个减为0个。QF201异常值误判数量由254个减为10个。可见通过浮标观测误差控制,可以大幅降低异常值误判数量。QF104准确异常值的判定率达到100%,QF201的准确异常值判定率为90.6% (106/117),两者均达到了较高的实用水平。Grubbs准则主要基于数据的统计性进行异常值检测,本研究限定数据数量不小于5个(公式(6))。作为对数量较少的数据序列中异常值判断的补充,我们在研究中加入局地性检测方法,在3个数据中寻找异常数据。这种简单有效的方法在QF104中检测出的异常值数量为7个,遗漏4个,错误个数为0。QF201中检测出的异常值个数为84个,其中遗漏39个,错误6个。该方法整体来看,存在一些遗漏的异常值,但是错误率较低,属于相对较为可靠的方法。局地检测方法一共涉及3个相邻数字(公式(4)),如果检测数据的前后数据中存在异常值,这就会对异常值判断造成影响,容易产生误判。图4第4 011个数的前后数据均为真实异常值,根据公式(4),第4 011个数也认定为局地异常值,造成误判。浮标201中存在大量斑块式异常数据(图3),有些大的异常数据中间存在正常数据,根据局地判定方法会认定中间数据为异常数据,因而也形成一些误判异常数据。
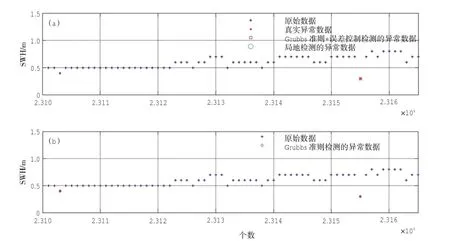
图2 QF104浮标有效波高数据质控局部情况示意图(a) 蓝星号为原始数据,红星号为真实异常数据,红框号为经Grubbs准则和误差控制检测的异常数据,绿圈为局地方法检测的异常数据;(b) 红钻石为Grubbs准则检测的异常数据
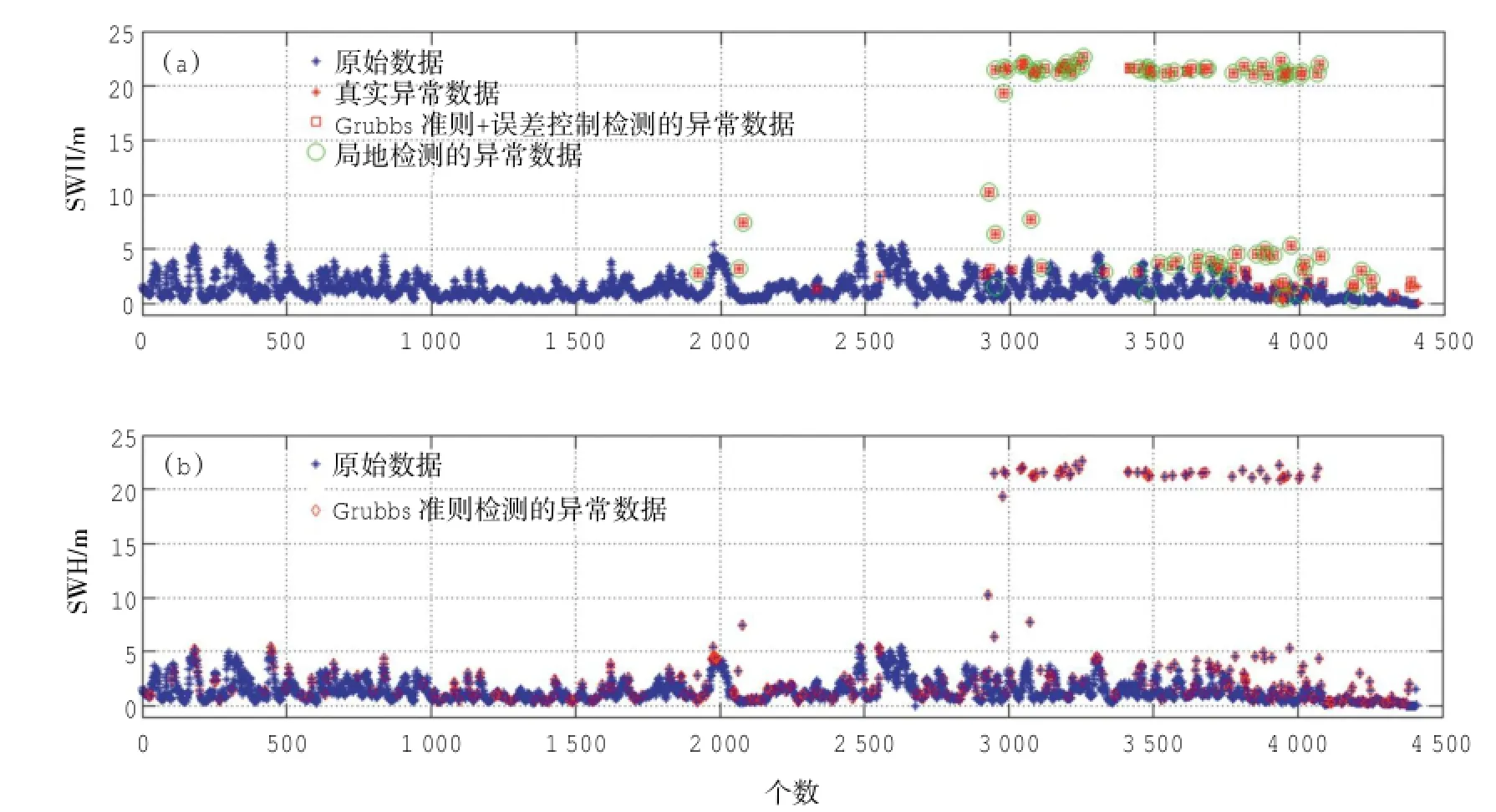
图3 QF201浮标有效波高数据整体质控情况(a)蓝星号为原始数据,红星号为真实异常数据,红框号为经Grubbs准则和误差控制检测的异常数据,绿圈为局地方法检测的异常数据;(b)红钻石为Grubbs准则检测的异常数据。
综合Grubbs准则、浮标观测误差控制和局地质控方法,QF104和QF201形成最终质控结果(表1,Grubbs准则+浮标误差控制+局地检测)。其中QF104,检测异常值个数为11,错误数和遗漏数均为0,即与准确异常值个数一致,且完全对应。QF201真实异常值个数为117个,检测个数为123个,检测正确个数为106个,遗漏11个,错判个数17个。如果异常数据为单个孤立型异常数据,Grubbs准则可以做出较为准确的判断(图1,图3)。如果异常数据大量出现,在局部时间内甚至超过正常数据的数量,这种情况下即使人工判断异常数据都较为困难,所以本文方法也出现了大量的漏判和错判(郭永幸,1994)。如图5,第3 980 和3 984个数据经Grubbs准则及浮标观测误差控制均认定为异常数据。从该段数据序列来看,数据连续性变化较为异常,有很大可能存在异常数据,但是仅从这些数据本身难以明确判定异常数据位置,因此人工判定时均认为是正常数据,所以对这两个数据的判定均为误判。
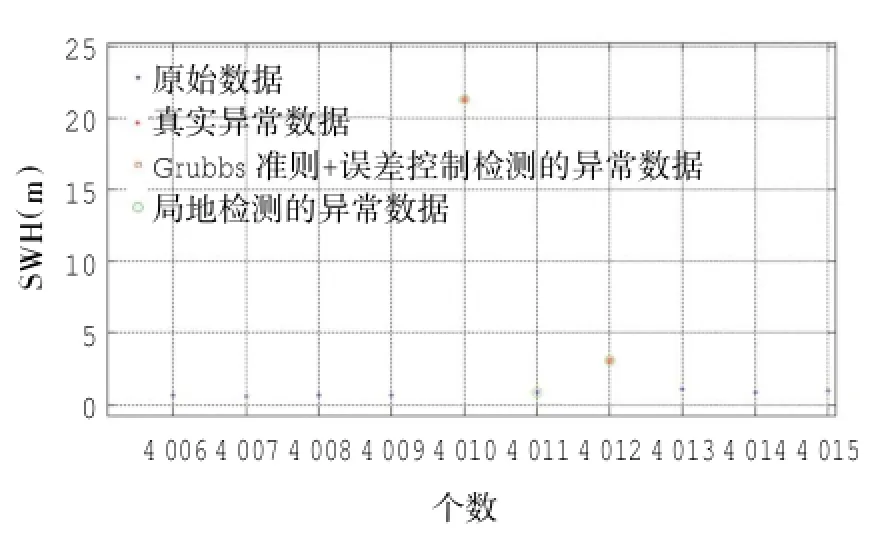
图4 QF201浮标有效波高数据质控局部情况示意图(蓝星号为原始数据,红星号为真实异常数据,红框号为经Grubbs准则和误差控制检测的异常数据,绿圈为局地方法检测的异常数据)。

图5 QF201浮标有效波高数据质控局部情况示意图蓝星号为原始数据,红星号为真实异常数据,红框号为经Grubbs准则和误差控制检测的异常数据,绿圈为局地方法检测的异常数据
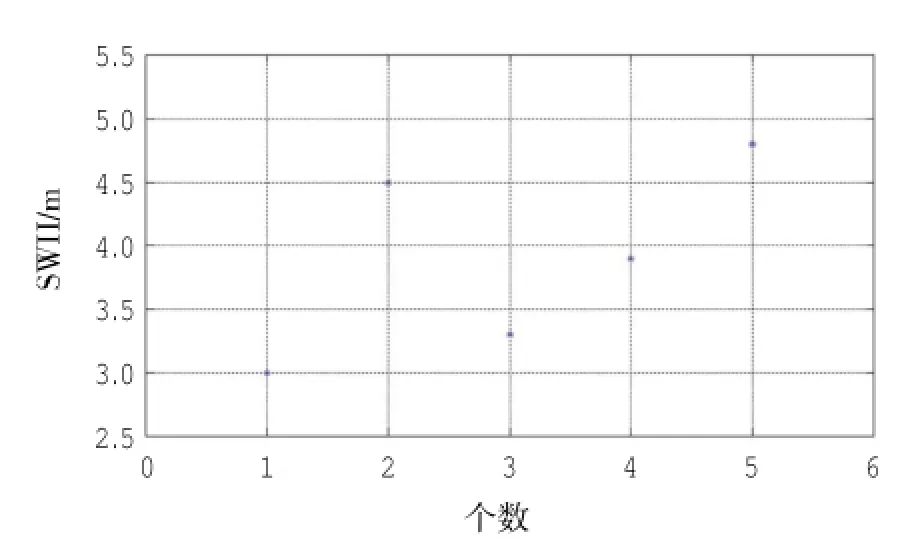
图6 数据序列 [3.0 4.5 3.3 3.9 4.8] 示意图
同样图5,以4 020到4 030时间段内的波高数据为例。在更长时间范围内看,第4 024-4028数据与前后时间段的数据变化趋势不符,观测值又全部相同,根据经验判定4 024-4 028数据均为异常数据。由于局部异常数据数量过多,且在长序列数据中统计特征无异常,这些异常数据是无法根据Grubbs准则和局地判定方法进行判断的。局部异常数据过多,就会导致正常数据成为少数数据,容易判定为异常数据,如4 029和4 030点就误判为异常数据点。
QF104浮标数据中的异常值点主要为单个孤立点,采用的研究方法能够比较准确的判定这些异常值点,判定的准确率为100%,遗漏率和错误率均为0。QF201中存在较多的异常值点,许多异常值以斑块形式出现,局部时间段异常值数量超过正常值数量。许多异常值即使人工方式都很难判断,因此我们采用的研究方法很难对异常值做到精确的判定。判定准确率仅为90.6%(106/117),遗漏率为9.4%。经分析发现,QF201数据中异常值如果较为明显(人工可明确判定),本文研究方法可以做到绝大部分判定。遗漏和错误判定点均出现在异常值不明显或人工都不能做出明确判定区域。
从QF104和QF201浮标数据质控情况看,Grubbs准则检测的异常值均包含了局地性检测方法的结果。Grubbs准则作为统计性检验方法,如果数据量为3~4个,容易产生误判,因此本研究限制数据量最小为5。存在一种异常数据在数据量较大时根据Grubbs准则难以判定为异常数据。如数据序列: [3.0 4.5 3.3 3.9 4.8](图6),第2个数据4.5在波高连续变化序列中容易认定为异常值,但是根据Grubbs准则不能判定4.5为异常数据。根据局地性判定方法就可以判断4.5为异常数据。因此尽管这种数据出现情况较少,但在理论上局地性检测方法仍然可以作为Grubbs准则的有效补充。
3 结论
通过统计质控方法、局地质控方法和浮标观测误差控制方法,对中国沿海两个具有代表性的浮标QF104和QF201进行了质控方法研究。其中浮标观测误差的控制可以大幅度降低异常值误判数量,是一种非常有效的浮标数据质控的控制条件。如果数据序列的异常值较为明显,该方法可以做出比较准确的判断。在数据序列的异常值不明显或者即使人工方式都难以做出判断时,该方法对于异常值判断的有效性降低,会出现一些遗漏和错判。整体来看,本文给出的异常值质控方法是针对浮标数据异常值质控非常有效的方法。根据本文研究分析,得出如下结论:
(1) Grubbs准则对于浮标有效波高时间序列数据中的统计异常值能够进行准确的质控,但是由于只是数学意义上的质控,会造成大量异常值的误判。通过加入浮标误差控制能够大幅度消减异常值误判情况,形成对真实异常值的有效质控。该思路同样可以应用于其他海洋环境参数的质控。
(2)局地性的异常值判定方法是一种简单有效的异常值质控方法。在保守的临界值系数(β=1.1)前提下,其在异常值判定的数量上相对较低,但是准确率高,误判情形少,在理论上可以作为Grubbs准则判定的有效补充。
(3)浮标观测数据异常值的成因与观测仪器本身、观测环境等要素密切相关,因此异常值的出现也具有比较复杂的外观特征。不存在能够质控所有异常值数据的理论方法,本文给出的Grubbs准则、浮标误差控制和局地性异常值判定的方法是简洁实用的时间序列数据质控方法,具备理论上的可靠性。本文研究方法对于局部区域出现多个连续不明显异常值时不能进行有效的质控,这也是本方法以后改进的聚焦点。
Grubbs F E,1950.Sample criteria for testing outlying observations.The Annals of Mathematical Statistics,27-58.
Hodge V J,Austin J,2004.A survey of outlier detection methodologies Artificial Intelligence Review,22(2):85-126.
National Oceanic and Atmospheric Administration,2009.Handbook of automated data quality control checks and procedures.Mississippi: NOAA.
SeaDataNet,2010.Data quality control procedures.Greece:SeaDataNet.
郭永幸,1994.试论“格拉布斯准则”的局限性.飞行试验,10 (2):35-40.
国家海洋局,2011a.HY/T 143小型海洋环境监测浮标.
国家海洋局,2011b.HY/T 142大型海洋环境监测浮标.
国家质量技术监督局,1998.GB 17378.2海洋监测规范第2部分:数据处理与分析质量控制.
黄谟涛,翟国君,王瑞,等,1999.海洋测量异常数据的检测.测绘学报,28(3):269-277.
李光强,2009.时空异常探测理论与方法.长沙:中南大学.
史静涛,周智海,2011.海洋站数据质量控制技术探讨.海洋技术学报,30(1):114-117.
王占全,2005.基于地理信息系统空间数据挖掘若干关键技术的研究.杭州:浙江大学.
杨筱,2009.卫星导航系统数据与信号质量评估技术研究.长沙:国防科学技术大学.
于婷,刘玉龙,杨锦坤,等,2013.实时和延时海洋观测数据质量评估方法研究.海洋通报,32(6):610-614.
郑琳,刘艳,崔文林,等,2014.海洋监测数据质量评估研究.海洋通报,33(2):228-234.
(本文编辑:袁泽轶)
A quality control method for the outlier detection of buoy observations
LIU Shou-hua,CHEN Man-chun,DONG Ming-mei,GAO Zhi-gang, ZHANG Jian-li,WU Shuang-quan,LIN Feng-zhu
(Nation Marine Data and Information Service,Tianjin 300171,China)
By combining Grubbs criteria,local outlier detection method and observation error control of wave height,a robust method is constructed for the quality control of wave height data.The results show that the performance of quality control for the buoy data is good,which reaches a relatively high level.By considering the observation error of wave height, the good quality data which are thought to be outlier or unusual by the old method could be detected well.The efficiency for the detection of outlier in the data records is good.And the method proposed by our study could be used in the quality control of other ocean factors observed by the buoy.
ocean buoy;outlier;quality control;Grubbs criteria
刘首华(1983-),男,博士,主要从事海浪、全球气候变化研究。电子邮箱:huazai950@hotmail.com。
P731
A
1001-6932(2016)03-0264-07
10.11840/j.issn.1001-6392.2016.03.004
2015-06-28;
2015-08-14
国家自然科学基金(41406032)。
