基于非2π周期三角方法的正常积分模拟与仿真

刘　姣，金国祥

武汉工程大学计算机科学与工程学院，湖北 武汉 430205

基于非2π周期三角方法的正常积分模拟与仿真

刘姣，金国祥*

武汉工程大学计算机科学与工程学院，湖北 武汉 430205

用非周期三角多项式作为逼近工具，对带Chebyshev权的正常积分构造两类求积公式：一类是将带Chebyshev权的正常积分变换成带另一权的正常积分，对后面的积分构造求积公式，然后利用变量逆变换将求积公式变为基于非周期三角多项式的原正常积分的求积公式；另一类是用正常积分的被积函数在非周期三角多项式生成子空间上的正交投影对被积函数进行逼近而得到求积公式；同时提出了这两种求积公式精度的概念.对上述两种求积公式在计算机上用MATLAB编程实现，当被积函数不是周期函数且不均匀时，得到的求积公式逼近效果优于传统意义下的求积公式，实验结果与理论分析相符.

非周期三角多项式；多项式逼近；求积公式

1　引言

用多项式（代数多项式或三角多项式）去逼近函数既是经典也是当今仍然比较活跃的一个研究课题，研究成果非常丰富［1-5］.由于计算机技术的广泛应用，推动了数值求积研究的进一步活跃，研究正常积分的数值计算人们通常都是在代数多项式或者三角多项式所生成的子空间中去构造求积公式，当被积函数不是周期函数且不均匀时，这种求积公式的近似效果并不理想，很少有人在介于代数多项式和三角多项式之间的非2π周期三角多项式（下面简称为非周期三角多项式）所生成的子空间中去构造求积公式.有关非周期三角多项式去逼近函数的研究文献并不多.1993年，D.Kosloff 和H.Tal-Ezer在研究一类偏微分方程的数值求解时，为了克服以Chebyshev多项式作为工具对空间离散化时会附加一些苛刻约束条件的困难，提出了带一时间步长约束的Chebyshev准谱方法［6］.在他们的研究中，首次提出了非周期三角多项式的概念.最近经研究发现，非周期三角多项式生成的子空间的逼近问题可应用到诸多研究领域（如函数逼近、数值积分、信号分析和压缩等）和工程实际问题之中；例如，用非周期三角多项式作为工具构造出正常积分求积公式在计算机研究领域中的机器学习方面有着直接的应用.2014年，H.Tal-Ezer对非周期三角多项式的逼近问题进行了一些研究［7］，H.Tal-Ezer讨论了非周期三角多项式的正交化及非周期三角多项式逼近解析函数的问题，作为结果的应用，他简单讨论了带Legendre权的正常积分的数值求积问题.

本文以非周期三角多项式作为工具，讨论了带Chebyshev权的正常积分

的两类求积公式，并首次提出这两类求积公式精度的概念，对求积公式在计算机上用MATLAB编程实现，从实验中数值实例的误差结果和解析图像知，当被积函数不是周期函数且不均匀时，基于非周期三角多项式所构造的求积公式近似效果优于传统意义下的求积公式，且实验结果与理论分析相符.

2　求积公式

2.1非周期三角多项式逼近

为了构造式（1）的基于非周期三角多项式的求积公式，引用文献［7］中的一些结果.

不失一般性，考虑定义域为［-1， 1］上的函数. 设Pk（y）为一组关于内积

和权函数ω（y）的正交多项式.

令

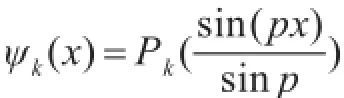
ψk（x）是一组关于内积

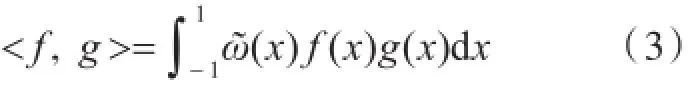
和权函数

的正交多项式.由ψk（x）生成的子空间记为Sn，即

由降幂公式知，Sn可写成由非周期三角多项式生成的子空间，即

其中

设 f是［-1 ， 1］上的连续函数，f在Sn上的正交投影为

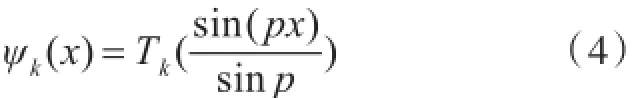
其中

为第一类Chebyshev多项式，其权函数为

由式（2）可得

由式（3）可得其中 β0=2，βk=1，k≥1.

设K为复平面C上的非空有界闭连通集，K的余集记作Kc.存在一个保角映射Ψ（ω），Ψ把单位圆的余集映射到Kc.令θ（y）为Ψ（ω）的逆映射，记

Bt表示Kc上的等位线，有下述定理，其证明见文献［8］.

定理假设 t ＞ 1 是使得F（y）在Bt内解析的最大数，Pn（y）是插值结点为的插值多项式，在K上均匀分布，则Pn（y）满足

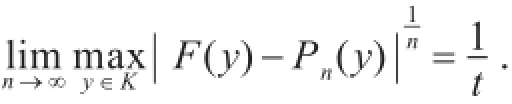
利用上述定理可计算收敛速率.取K=［-1 ， 1］，由文献［9］知，保角映射为

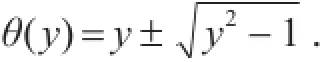
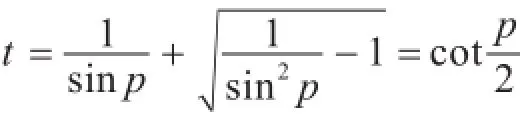
于是渐近收敛速率为

因此，用式（4）逼近函数时，其渐近精度为cε，其中

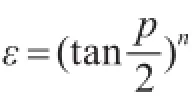
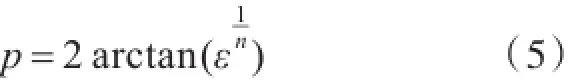
其中对ε的选择取决于精度的需要，类似地，对n的选择同样如此.

由于对 p的选择不依赖于被逼近的函数.通过最小化算法找一个参数 p使误差向量的范数最小，而 p适合所有函数，这里误差向量范数定义为

其中 zj为在区间［a，b］上随机分布的检测点，1≤j≤m.

2.2带Chebyshev权的正常积分求积公式

用非周期三角多项式作为工具，构造式（1）的第一类求积公式.利用式（2）对式（1）进行变换，得

其中

由式（2）可知

由Gauss求积公式［10］，构造式（6）的求积公式

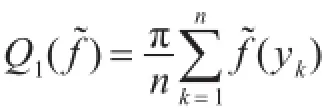
其中 yk为 Tn（y）的零点，即， k=1 ， 2 ，… ，n，

其中

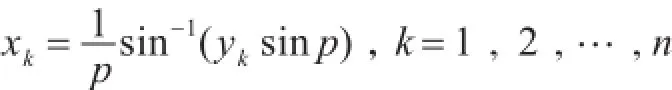
于是

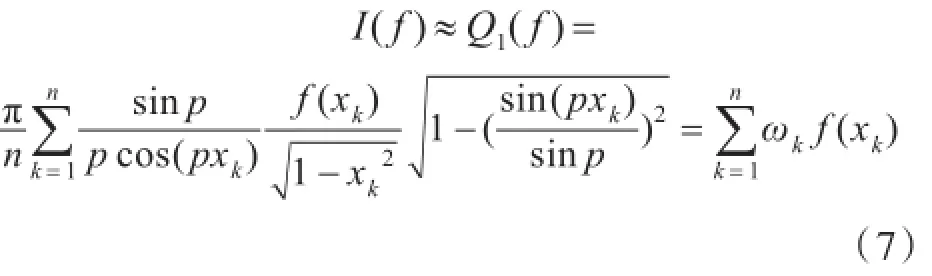
其中

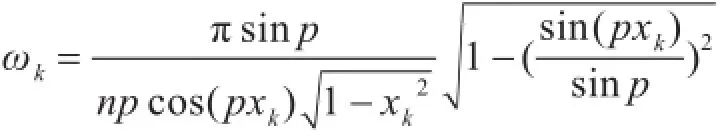
式（7）是基于非周期三角多项式的带Chebyshev权正常积分的第一类求积公式，它至少在… ，n所张成的空间中是精确的.

下面构造式（1）的第二类求积公式.用被积函数 f在ψk张成的空间上的正交投影 fn去替代式（1）中的 f，可以得到式（1）的另一类求积公式为

其中

求积公式Q2（f）至少在， k=0 ，1 ，2 ，…，n所生成的空间中是精确的.

3　结果与讨论

对带Chebyshev权的正常积分的经典Gauss型求积公式和基于非周期三角多项式的求积公式（7）、（8）用MATLAB进行仿真实验，通过误差数据表和图像说明求积公式的误差渐进性.误差定义如下：

非周期三角多项式中的参数 p可用两种方法计算.一种是根据式（5）进行计算，取 ε=10-15，此时参数 p记作 p1，得到的非周期三角多项式记为Nptp1.另一种是通过最小化算法，找到一个 p使得误差向量范数E最小，此时参数 p记作 p2，得到的非周期三角多项式记为Nptp2.例1、例2是对经典Gauss型求积公式和基于Nptp1的求积公式（7）进行数值实现，例3是对用Chebyshev多项式逼近被积函数而构造的求积公式和基于Nptp1、Nptp2的求积公式（8）进行数值实现.

例1函数 f（x）=e-50x2.

取结点个数n为10，20，40，求积结果如表1、图1所示.

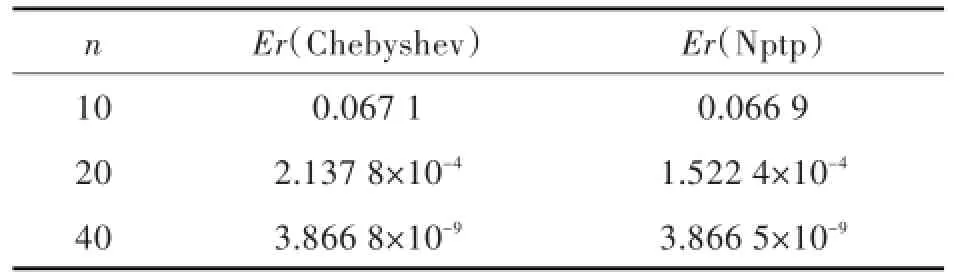
表1　f（x）=e-50x2求积公式误差Tab.1　Error of the quadrature formulae forf（x）=e-50x2

图1　f（x）=e-50x2求积公式误差曲线Fig.1　Error curves of the quadrature formulae forf（x）=e-50x2

例2函数 f（x）=xsin（2x）cos（3x）

取结点个数n为10，20，40，求积结果如表2、图2所示.

例3f（x）=e-30x2

取结点个数n为6，12，15，求积结果如表3所示.

表2　f（x）=xsin（2x）cos（3x）求积公式误差Tab.2　Error of the quadrature formulae forf（x）=xsin（2x）cos（3x）

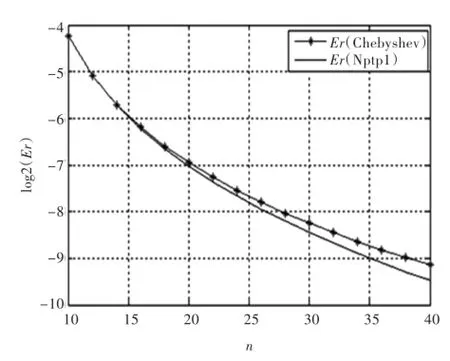
图2　f（x）=xsin（2x）cos（3x）求积公式误差曲线Fig.2　Error curves of the quadrature formulae for f（x）=xsin（2x）cos（3x）

表3　f（x）=e-30x2求积公式误差Tab.3　Error of the quadrature formulae forf（x）=e-30x2

对带Chebyshev权正常积分的被积函数设计多个具体实例，用MATLAB语言对基于非周期三角多项式的两类求积公式（7）、（8）和经典Gauss型求积公式在计算机上进行了实验，由这三个实验知，随着n的不断增大，三种求积公式的误差均逐渐减小；由于所取的函数都不是周期函数且并不均匀，本文所得到的求积公式（7）、（8）的近似效果优于经典Gauss型求积公式；另外，由例3知，由于所取的函数在中间区域有大梯度，Nptp2中的p是通过最小化算法得到的最优p，基于Nptp2的求积公式近似效果优于其它两种求积公式，这与理论分析相符.

由于受设备条件的限制，选取的结点数比较少，因此各求积公式的误差区别并不太明显，若选取更多的结点，非周期三角多项式构造的求积公式的优越性将会更加显著.

4　结语

用非周期三角多项式作为逼近工具，对带Chebyshev权的正常积分构造了两类求积公式：一类是将带Chebyshev权的正常积分变换成带另一权的正常积分，对变换后的积分构造求积公式，然后利用变量逆变换将求积公式变为基于非周期三角多项式的原正常积分的求积公式；另一类是用正常积分的被积函数在非周期三角多项式生成子空间上的正交投影对被积函数进行逼近而得到求积公式；这两类求积公式丰富了Gauss数值求积的内容，目前还是未见诸文献的求积公式，本文给计算机研究领域的机器学习的算法提供了一些理论基础，对该算法在大数据挖掘中的速度及准确率的提高都有帮助.

在对正常积分进行数值计算时，当被积函数不是周期函数且不均匀时，所得到的基于非周期三角多项式的求积公式的近似效果要优于经典Gauss型求积公式.从实验结果可看出，基于非周期三角多项式的求积公式误差小于经典Gauss型求积公式，尤其是当非周期三角多项式中的参数p为通过最小化算法得到的最优 p时，基于非周期三角多项式的求积公式的优越性则更加明显.实验结果与理论相符.

［1］DIKUSAR N D.Higher-order polynomial approximation［J］.Mathematical models and computer simulations，2016（8）：183-200.

［2］IRODOVA I P.Piecewise polynomial approximation methods in the theory of Nikol'Skiǐ-Besov spaces［J］. Journal of mathematical sciences，2015（209）：319-480.

［3］ SHESTAKOV O V.Reconstructing distributions of multivariate random functions under orthogonal polynomial projection approximation［J］.Journal of mathematical sciences，2014（196）：78-83.

［4］KOPOTUN K A.Polynomialapproximationwithdoubling weights［J］.Acta mathematica hungarica，2015（146）：496-535.

［5］ DANIELYAN A A.Weak-star convergence and a polynomial approximation problem［J］.Results in mathematics，2016（69）：257-262.

［6］KOSLOFF D，HILLEL T.Modified chebyshev pseudospectral methods with O（N-1）time step restriction［J］. Journal of computational physics，1993（104）：457-469.

［7］HILLELT.Nonperiodictrigonometricpolynomial approximation［J］.Journal of scientific computing，2014 （60）：345-362.

［8］WALSH J L.Interpolation and approximation by rational functions in the complex domain［M］.Providence：American Mathematical Society，1956.

［9］MARKUSHEVICH A I.Theory of functions of a complex variable［M］.New York：Chelsea，1977.

［10］纳唐松И П.函数构造论（下册）［M］.北京：科学出版社，1959.

本文编辑：陈小平

Simulation and Emulation of Proper Integrals Based on Non-2π-Periodic Trigonometric Method

LIU Jiao，JIN Guoxiang*

School of Computer Science and Engineering，Wuhan Institute of Technology，Wuhan 430205，China

We constructed two kinds of quadrature formulae of the proper integral with Chebyshev weight using the nonperiodic trigonometric polynomials as the approximate tool.First，we constructed the quadrature fomula of the integral with a new weight transformed from the integral with Chebyshev weight.And then，we transformed it by the inverse transform of the variable to get the first quadrature formula of the original integral based on the nonperiodic trigonometric polynomials.We obtained the second quadrature formula by using the orthogonal projection of the integrand on the subspace spanned by the nonperiodic trigonometric polynomials to approximate the integrand.Meanwhile，we presented the precision conception of the two quadrature formulae.We emulated the two kinds of quadrature formulae with MATLAB.The approximation effects of the two quadrature formulae are better than those of the quadrature formulae in general when the integrand is nonperiodic and non-uniform，which consistents with our theoretical analysis.

nonperiodic trigonometric polynomials；polynomials approximation；quadrature formulae

金国祥，博士，教授.E-mail：gxjin521@163.com

O241.38 O174.41

A

10.3969/j.issn.1674-2869.2016.04.016

1674-2869（2016）04-0399-05

2016-04-06

刘姣，硕士研究生.E-mail：372862510@qq.com