基于粒子群算法与最小二乘支持向量机的ET0模拟
2016-08-13王嘉毅
鞠 彬,王嘉毅
(1.河海大学水文水资源学院,江苏 南京 210098; 2.中国电建集团华东勘测设计院有限公司,浙江 杭州 310014;3.河海大学水利水电学院,江苏 南京 210098)
基于粒子群算法与最小二乘支持向量机的ET0模拟
鞠彬1,2,王嘉毅3
(1.河海大学水文水资源学院,江苏 南京210098; 2.中国电建集团华东勘测设计院有限公司,浙江 杭州310014;3.河海大学水利水电学院,江苏 南京210098)
摘要:以月最高气温、月最低气温、月平均气温、平均风速、日照时数以及相对湿度6个气象因子的不同组合作为输入数据,以FAO Penman-Monteith公式计算结果作为标准值,构建基于粒子群优化算法与最小二乘支持向量机的ET0预测模型(PSO-LSSVM)。选取新疆额尔齐斯河流域哈巴河气象站1986—2013年的气象数据进行模型训练与预测,并与其他常用ET0计算公式进行对比研究。结果表明,PSO-LSSVM模型能够很好地反映ET0同各气象因子之间的非线性关系,其中气温条件是影响ET0模拟精度最重要的因素,同时随着气象因子输入的减少PSO-LSSVM模型模拟精度有所下降;当分别基于辐射条件、温度条件计算时,PSO-LSSVM模型模拟结果较Priestley-Taylor公式、Hargreaves-Samani公式计算结果要优。基于多因子量化指标的ET0预测模型实现了精度和实用性的统一,可为缺资料地区ET0研究预报提供科学参考。
关键词:参考作物蒸发蒸腾量;气象因子;粒子群算法;最小二乘支持向量机;额尔齐斯河流域
参考作物蒸发蒸腾量(ET0)是计算作物需水量的关键指标,对于地区作物干旱监测、农业灌溉与排水、提高农业用水效率等具有重要意义[1]。国内外关于ET0的计算公式较多,如FAO Penman-Monteith、Priestley-Taylor[2]、Hargreaves-Samani[3]公式等。目前应用较多的是联合国粮农组织推荐使用的FAO Penman-Monteith公式,研究表明其具有较高的计算精度和地区适用性[4]。但FAO Penman-Monteith公式较为复杂,参数过多,不仅需要每日的气象资料,还需要海拔、纬度、太阳磁偏角等多个地理参数,需要建立专门的气象站点进行观测[5],给FAO Penman-Monteith公式的推广使用带来不便。
ET0受气象因子影响强烈,是一个复杂的非线性系统。近年来随着机器学习理论的不断发展,出现了许多用于分析复杂非线性关系的模型,如人工神经网络模型[6]、支持向量机[7]、贝叶斯网络模型[8]等。徐俊增等[9]探讨了人工神经网络模型及其在ET0模拟中的应用;侯志强等[10]利用最小二乘支持向量机对河套地区日尺度下的ET0模拟进行研究。但是人工神经网络模型学习样本数量较大,收敛速度较慢,且存在局部极值和过学习问题;而最小二乘支持向量机的模型参数十分敏感,模型预测精度受参数取值的影响明显。因此,如何兼顾搜索的广度和速度,寻求能表述ET0特性且预测精度高的ET0预测模型,具有重要的理论意义和应用价值。
本文选取新疆额尔齐斯河流域哈巴河气象站1986—2013年的气象数据资料,以各气象因子间的不同组合方式作为模型的输入,构建基于粒子群优化算法和最小二乘支持向量机的ET0预测模型(PSO-LSSVM),并以FAO Penman-Monteith公式计算结果作为模型预期输出值进行训练与预测,并与其他常用ET0计算公式的计算结果进行对比研究,分析PSO-LSSVM模型的精度与适用性,为今后ET0的预报研究提供一种新的思路与方法。
1 研究区域概况
额尔齐斯河流域位于新疆阿尔泰地区东北部,东经85°35′~90°30′,北纬46°52′~49°15′。其在我国境内全长546 km,年径流量多达119亿m3,水量仅次于伊犁河,是我国境内唯一一条流入北冰洋的国际河流。
额尔齐斯河流域具有典型的大陆性干旱气候特征,光照丰富,温度日变化大,降水量少,蒸发量大[11]。新疆是中国5大牧区之一,而额尔齐斯河流域所在地阿尔泰地区又是新疆最主要的牧区之一,因此进行流域内ET0的模拟研究,对发展地区节水灌溉、确定合理的灌溉制度具有重要的意义[12]。
选取额尔齐斯河流域内典型气象站点哈巴河(48.05°N,86.4°E)1986—2013年的气象资料进行ET0的模拟研究,气象资料来源于国家气象局资料中心。由于FAO Penman-Monteith公式计算时间步长为日,故需要先计算每日ET0值,从而得到各月ET0值,再在月尺度上进行ET0的模拟。
2 模型构建
2.1研究方法
2.1.1最小二乘支持向量机
支持向量机(SVM)是由Vapnik提出的一种能够处理回归和模式识别等诸多问题的新型统计学方法[13]。支持向量机建立在统计学的VC维理论和结构风险最小化原则的基础上,能较好地解决以往学习方法中存在的过学习、非线性、局部极值点以及高维数等实际问题[14]。
最小二乘支持向量机算法(LS-SVM)于2001年由Suykens提出,其优化指标采用了平方项,将传统支持向量机中的不等式约束改为等式约束,把二次规划问题转化成线性方程组的求解问题,大大简化了模型计算的复杂性[15]。其原理如下:
设样本为n维向量,某区域的l个样本(x1,y1),(x2,y2),…,(xl,yl)∈Rn×R,采用非线性映射将样本从原空间Rn映射到特征空间φ(xi),并在这个高维特征空间中构造最优决策函数:
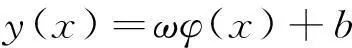
(1)
定义以下优化问题:
(2)
式中:ω为权系数向量;b为偏量系数;J为优化目标函数;c为惩罚因子;ei为松弛因子。
采用拉格朗日法求解上述优化问题
(3)
式中αi为Lagrange乘子。
根据最优条件,并定义核函数为K(xi,xj)=φ(xi)Tφ(xj),将二次规划问题转化为求解线性方程组的求解问题:
(4)
利用最小二乘法求α、b。得到LS-SVM模型:
(5)
其中核函数一般采用RBF函数:
(6)
式中σ为核函数宽度参数。
2.1.2粒子群优化算法
模型预测精度的高低,与模型参数的取值关系密切,LS-SVM模型参数c、σ在很大程度上决定了最小二乘支持向量机的学习和泛化能力,目前常采用的传统优化算法费时费力,而且率定出来的结果离最优值相距甚远。本文采用粒子群算法(article swarm optimization,简称PSO)对参数c、σ进行寻优。粒子群优化算法是由berhart等[16]提出的一种群智能仿生优化算法,具有收敛速度快、全局寻优能力、不会陷入维数灾问题等突出优点。其原理如下:
算法初始化时随机产生一群粒子(m个),即优化问题的随机解,其中第k次迭代第i个粒子的空间位置表示为:Xi=(xi1,xi2,…,xid)T,Vi=(vi1,vi2,…,vid)T,(i=1,2,…,m)。粒子群算法寻找优解时,各粒子是根据下式(7)和式(8)来更新自己的速度和位置,将其代入优化目标函数可以计算出相应的适应度值来衡量xik的优劣。粒子目前找到的最优解,称为个体极值(pi),整个种群目前找到的最优解,称为全局极值(pg),在每一次迭代中,粒子通过这两个“极值”来更新自己。
(7)
(8)
式中:c1、c2为学习因子,一般c1=c2,并且在0~4的范围内;rand()为介于(0,1)之间的随机数;ω为惯性权重,为非负常数。
2.1.3PSO-LSSVM耦合模型
本文采用粒子群优化算法(PSO)对LS-SVM模型参数c、σ进行优选,PSO-LSSVM耦合模型的算法流程图如图1所示。
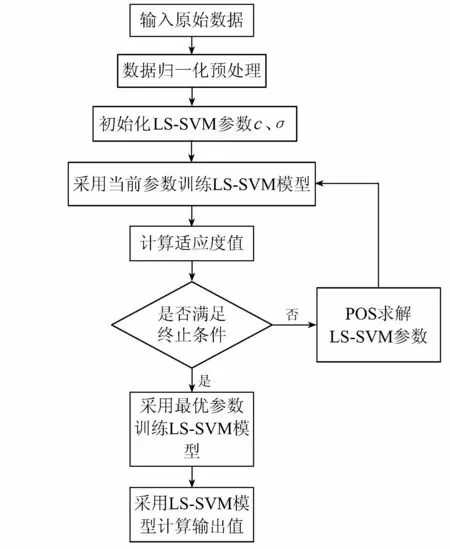
图1 PSO-LSSVM模型算法流程
PSO优选LS-SVM模型参数c、σ的步骤如下:
a. 生成初始种群,包括种群规模、迭代次数、初始粒子速度和位置等。
b. 利用LS-SVM模型对测试样本进行预测,建立适应度函数f(x),计算每个个体的适应度函数值。
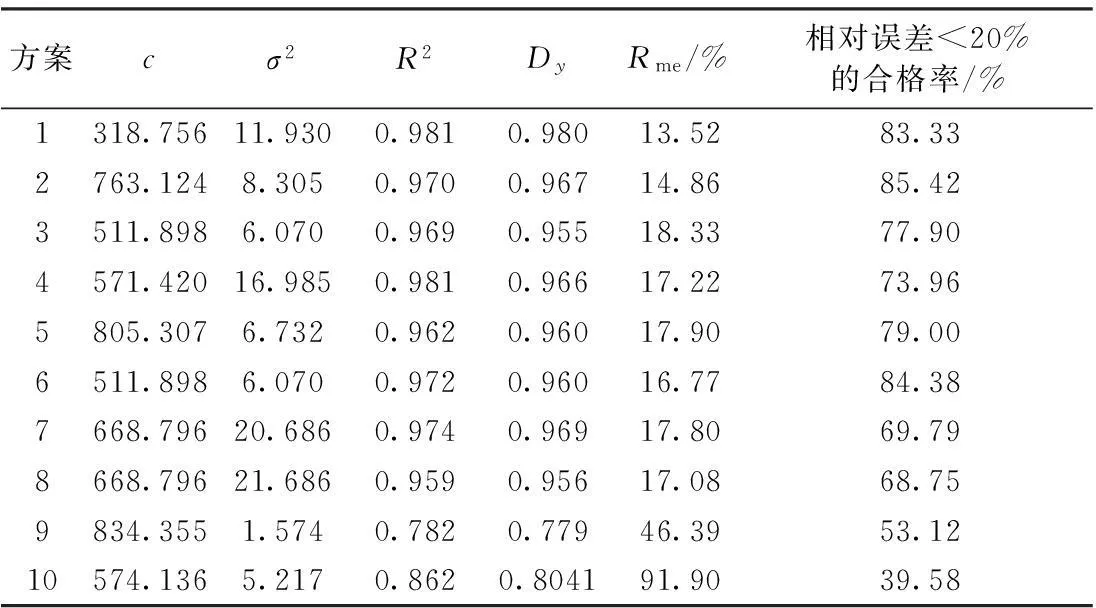
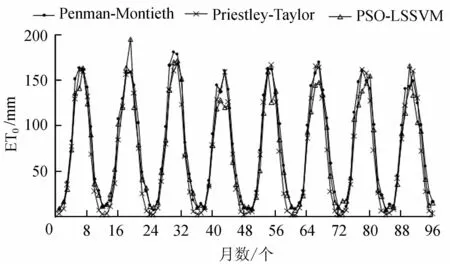
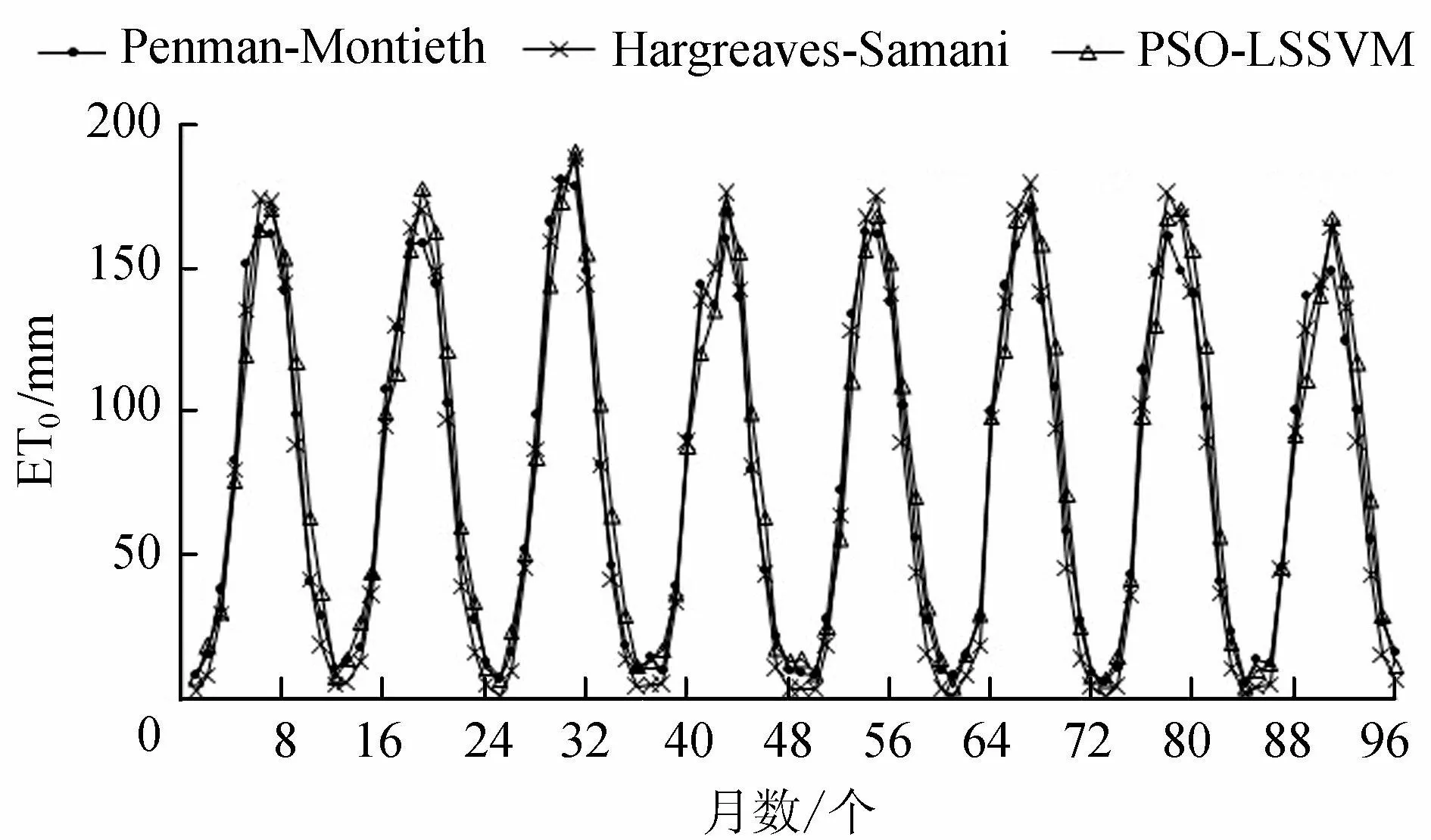
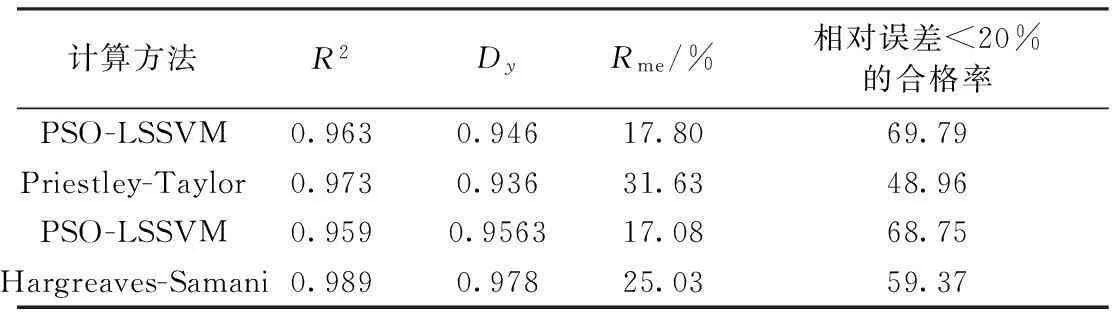
c. 计算的适应度函数值f与粒子目前已找到的最优适应值fbest进行比较。如果f d. 将每个粒子的最优适应值fbest与所有粒子的最优适应值fBest进行比较。如果fbest e. 判断适应值是否满足要求,如不满足要求,按式(7)、式(8)将粒子进行更新,从而产生新的粒子(即新的解),返回步骤(b),重复进行新一轮的计算。如果适应值满足要求,计算结束。 2.2组合方案 选用与参考作物蒸发蒸腾量(ET0)有紧密联系的6个气象因子进行研究,分别为:月最高气温、月最低气温、月平均气温、平均风速、日照时数以及相对湿度。在6个气象因子中分别取2~6个因子进行排列组合,共有10种组合方案(表1),分析不同气象因子组合方式下的PSO-LSSVM模型的模拟精度。 本文采用FAO推荐使用的FAO Penman-Montieth公式的计算结果作为PSO-LSSVM模型的预期输出值,且将模型拟合结果与其他两种常用的ET0计算公式(Hargreaves-Samani、Priestley-Taylor)进行比较研究,FAO Penman-Monteith、Hargreaves-Samani、Priestley-Taylor公式的表达形式如式(9)、(10)、(11)所示。 (9) (10) (11) 表1 不同气象因子组合方式 2.3评价指标 采用平均相对误差Rme、相关系数R2、确定性系数Dy来衡量模型预测值与计算值之间的拟合精度。各统计量的具体公式如下: (12) (13) (14) 3.1PSO-LSSVM模型模拟结果分析 采用哈巴河气象站1986—2013年逐月气象数据资料进行研究,其中1986—2005年共240个样本用于PSO-LSSVM模型训练,2006—2013年共96个样本用于PSO-LSSVM模型预测。不同气象因子组合下的预测结果如表2所示。 从表2可以看出,当采用6个气象因子进行ET0模拟计算时(方案1),PSO-LSSVM模型的模拟结果与FAO Penman-Montieth公式计算结果拟合程度最高(R2=0.981),平均相对误差仅为13.52%,样本中相对误差落在20%误差范围线内的合格率为83.33%。可以看出,当采用6个气象因子进行ET0模拟时,PSO-LSSVM模型体现出较高的预测精度,能够很好地反映各气象因子同ET0之间的非线性关系。 表2 不同气象因子组合下的模拟结果 当采用5个气象因子进行ET0的模拟计算时(方案2、3、4),PSO-LSSVM型依然能够较好的预测ET0值。在3种不同气象因子的组合下,各方案模拟结果的R2和Dy均在0.9以上。其中在仅缺少相对湿度的情况下(方案2),样本平均相对误差为14.86%,相对误差小于20%的样本个数占85.42%,模拟精度较方案1略有下滑,可见相对湿度这一气象因子对于ET0模拟计算影响较小;当缺少平均风速这一气象因子时(方案3),ET0模拟精度下滑幅度为3个方案中最大,PSO-LSSVM型平均相对误差达到18.33%,相对误差落在20%误差范围线内的样本数占77.9%;当缺少日照时数这一气象因子进行模拟时(方案4),PSO-LSSVM型平均相对误差值为17.22%,模拟结果中相对误差小于20%的样本数仅占73.96%,可见平均风速、日照时数这两个气象因子对ET0模拟计算的影响程度较为一致,且两者较相对湿度这一因子对ET0的预测精度影响更大。 当采用4个气象因子进行ET0模拟计算时(方案5、6、7),各方案模拟精度均略有下降,但3者ET0模拟精度的差距不大。当仅采用3个气象因子进行ET0模拟计算时(方案8、9),两方案的模拟精度差异较大,当缺少平均风速、日照日数、相对湿度这3个气象因子进行模拟时,PSO-LSSVM模拟结果的平均相对误差为17.08%,与方案1相比发生小幅度的下滑,但模拟结果中相对误差落在20%误差范围线内的样本个数仅占68.75%;当缺少温度条件时,ET0模拟精度较其他几种组合方式都要差,相关系数R2仅为0.782,平均相对误差值高达46.39%,相对误差小于20%的样本个数仅占53.12%,可见温度条件对于ET0而言是十分重要的因素。 当仅用2个气象因子进行模拟计算时(方案10),模拟结果的平均相对误差高达91.9%,相对误差小于20%的样本数仅占39.58%,明显低于上述任何组合方式的模拟结果,已经无法满足实际生产的精度需要。 3.2与其他ET0计算公式的比较 当研究区域缺乏气象资料而无法使用FAO Penman-Montieth公式计算ET0时,多采用一些基于辐射或温度资料的半经验性方法来估算ET0,如以平均温度和温差为主要参数的Hargreaves-Samani方法,曾被FAO推荐为资料不满足FAO Penman-Monteith公式时的替代计算方法;还有以辐射资料进行估算的代表方法Priestley-Taylor公式。本文将PSO-LSSVM模型与上述两个常用替代公式进行对比研究,分析PSO-LSSVM模型的精度与适用性。 图2为Priestley-Taylor公式、FAO Penman-Monteith公式、PSO-LSSVM模型2006—2013年各月ET0计算结果;图3为Hargreaves-Samani公式、FAO Penman-Monteith公式、PSO-LSSVM模型2006—2013年各月ET0计算结果;表3为Priestley-Taylor公式、Hargreaves-Samani公式、PSO-LSSVM模型模拟结果中各评价指标的比较。 图2 基于辐射条件时不同方法的计算结果 图3 基于温度条件时不同方法的计算结果 计算方法R2DyRme/%相对误差<20%的合格率PSO-LSSVM0.9630.94617.8069.79Priestley-Taylor0.9730.93631.6348.96PSO-LSSVM0.9590.956317.0868.75Hargreaves-Samani0.9890.97825.0359.37 从图2可以看出,当基于辐射资料计算时,Priestley-Taylor公式的计算结果、PSO-LSSVM模型模拟结果都与FAO Penman-Montieth公式的计算结果具有相同的变化趋势,其中PSO-LSSVM模型同FAO Penman-Montieth公式的计算结果更为接近,拟合精度较Priestley-Taylor公式要高;PSO-LSSVM模型在极小值点拟合情况较好,极大值点易出现计算结果偏大的情况,而Priestley-Taylor公式的计算结果整体呈现偏小现象,极小值点偏小情况更为严重,分析其原因,可能是由于Priestley-Taylor公式并没有将风速考虑在内,从而导致当风速较大时该方法的计算值往往偏小。从表3也可以看出,Priestley-Taylor公式计算结果的平均相对误差为31.63%,相对误差落在20%误差范围线内的样本比例为48.96%,远低于PSO-LSSVM模型的模拟精度。 从表3可以看出,当基于温度条件进行ET0的模拟计算时,PSO-LSSVM模型的模拟精度较Hargreaves-Samani公式要高,但Hargreaves-Samani公式计算所得的R2和Dy等评价指标均好于PSO-LSSVM模型,从图3可以看出,Hargreaves-Samani公式受温度影响较大,当冬季和春节气温较低时其计算结果往往偏小,而6、7月份时Hargreaves-Samani公式和PSO-LSSVM的计算结果均呈现偏大趋势,全年其他月份FAO Penman-Montieth法、Hargreaves-Samani公式、PSO-LSSVM模型3者差距不大,拟合精度都很高。 a. 以新疆额尔齐斯河流域哈巴河气象站1986—2013年的气象资料为基础构建PSO-LSSVM模型,研究不同气象因子组合方案作为模型输入条件时的模拟效果。结果表明基于粒子群优化算法与最小二乘支持向量机的ET0预测模型(PSO-LSSVM)能够很好地反映不同气象因子同ET0之间的非线性关系,且随着气象因子输入的减少模型模拟精度也有所降低,其中方案1精度最高(R为13.52%,R2为0.981,Dy为0.980,样本中相对误差落在20%误差范围线内的合格率为83.33%),其次为方案2和方案6,也具有很高的精度和实用性。各气象因子中,温度条件对ET0的模拟精度有很大的影响,而相对湿度影响不大,平均风速和日照时数影响程度居中。 b. 当仅基于温度条件进行ET0的模拟计算时,温度较低的情况下采用Hargreaves-Samani公式计算结果会出现偏小的情况,需要进行修正,此时采用PSO-LSSVM模型模拟结果更为精确,而当温度较高时两者拟合精度相差不大;当仅基于辐射资料进行ET0的模拟计算时,运用Priestley-Taylor公式的计算结果会出现偏小的情况,采用PSO-LSSVM模型模拟结果要优于Priestley-Taylor公式。当缺乏气象数据而无法采用已有的公式进行计算时,采用PSO-LSSVM模型也可以得到较为精确的ET0计算结果。 c. 基于多因子量化指标的ET0预测模型,体现了不同气象因子对ET0影响的相对程度,实现了精度和实用性的统一,可为缺资料地区ET0的预测研究提供了一种新的观点和途径。 参考文献: [1] 康绍忠.新的农业科技革命与21世纪我国节水农业的发展[J].干旱地区农业研究,1998,16(1): 11-17.(KANG Shaozhong.New agricultural sci-technological revolution and development of Chinese water-saving agriculture in 21st century[J].Agriculturai Research in the Arid Areas,1998,16(1):11-17.(in Chinese)) [2] 刘晓英,林而达,刘培军.Priestley-Taylor与Penman法计算参照作物腾发量的结果比较[J].农业工程学报,2003,19(1):32-36.(LIU Xiaoying,LIN Erda,LIU Peijun.Comparative study on Priestley-Taylor and Penman methods in calculating reference crop evapotranspiration[J].Transactions of the CSAE,2003,19(1):32-36.(in Chinese)) [3] 彭世彰,徐俊增.参考作物蒸发蒸腾量计算方法的应用比较[J].灌溉排水学报,2004,23(6):5-9.(PENG Shizhang,XU Junzeng.Comparison of reference crop evapotranspiration computing methods[J].Journal of Irrigation and Drainage,2004,23(6):5-9.(in Chinese)) [4] 毛飞,张光智,徐祥德.参考作物蒸散量的多种计算方法及其结果的比较[J].应用气象学报,2000,11(增刊1):128-136.(MAO Fei,ZHANG Guangzhi,XU Xiangde.Several methods of calculating the reference evapotranspiration and comparison of the results[J].Quarterly Journal of Applied Meteorology,2000,11(sup1):128-136.(in Chinese)) [5] 王玉宝,汪志农,尚虎君,等.参考蒸发蒸腾量测定仪器的研究与开发[J].灌溉排水学报,2004,23(3): 61-64.(WANG Yubao,WANG Zhinong,SHANG Hujun.et al.Developing an instrument to measure crop evapotranspiration[J].Journal of Irrigation and Drainage,2004,23(3): 61-64.(in Chinese)) [6] 王文圣,丁晶,刘国东.人工神经网络非线性时序模型在水文预报中的应用[J].四川水力发电,2000,19(增刊1):8-10.(WANG Wensheng,DING Jing,LIU Guodong.Application of artificial neural network model with nonlinear time series in hydrologic forecast[J].Sichuan Water Power,2000,19(sup1):8-10.(in Chinese)) [7] 廖杰,王文圣,李跃清,等.支持向量机及其在径流预测中的应用[J].四川大学学报(工程科学版),2006,38(6):24-28.(LIAO Jie,WANG Wensheng,LI Yueqing,et al.Support vector machine method and its application to prediction of runoff[J].Journal of Sichuan University(Engineering Science Edition),2006,38(6):24-28.(in Chinese)) [8] 慕春棣,戴剑彬,叶俊.用于数据挖掘的贝叶斯网络[J].软件学报,2000,11(5): 660-666.(MU Chundi,DAI Jianbin,YE Jun.Bayesian network for data mining[J].Journal of Software,2000,11(5): 660-666.(in Chinese)) [9] 徐俊增,彭世彰,张瑞美,等.基于气象预报的参考作物蒸腾蒸发量的神经网络预测模型[J].水利学报,2006,37(3):376-379.(XU Junzeng,PENG Shizhang,ZHANG Ruimei,et al.Neural network model for reference crop evapotranspiration prediction based on weather forecast[J].Journal of Hydraulic Engineering,2006,37(3):376-379.(in Chinese)) [10] 侯志强,杨培岭,苏艳平,等.基于最小二乘支持向量机的ET0模拟计算[J].水利学报,2011,42(6):743-749.(HOU Zhiqiang,YANG Peiling,SU Yanping,et al.Simulation of ET0based on LS-SVM method[J].Journal of Hydraulic Engineering,2011,42(6):743-749.(in Chinese)) [11] 李定枝.额尔齐斯河流域水文特性[J].水文,1999(3):54-57.(LI Dingzhi.Hydrological characteristics on Irtysh Basin[J].Journal of China Hydrology,1999(3):54-57.(in Chinese)) [12] 廖显琴,李毅.参考作物腾发量计算方法的适用性研究[J].灌溉排水学报,2009,28(6): 14-17.(LIAO Xianqin,LI Yi.Adaptability research of different reference crop evapotranspiration estimated methods in Shaanxi[J].Journal of Irrigation and Drainage,2009,28(6):14-17.(in Chinese)) [13] VAPNIK V N.The Nature of Statistical Learning Theory [M].New York: Springer,1995. [14] VAPNIK V N.An overview of statistical learning theory [J].IEEE Trans Neural Network,1999,10(5): 988-999. [15] SUYKENS J A K,GESTEL T V,BRABANTER J D,et al.Least squares support vector machines [M].Singapore: World Scientific Publishing Co.,2002. [16] Kennedy J,Eberhart R.Particle swarm optimization[C]//Proceeding of IEEE international conference on neural networks.Piscataway: IEEE CS,1995:1942-1948. DOI:10.3880/j.issn.1004-6933.2016.04.012 作者简介:鞠彬(1991—),男,硕士研究生,研究方向为水文学及水资源。E-mail:hhu_09jubin@163.com 中图分类号:S161.4 文献标志码:A 文章编号:1004-6933(2016)04-0074-06 (收稿日期:2016-02-22编辑:徐娟) Simulation of ET0based on particle swarm optimization and least squares support vector machine JU Bin1,2, WANG Jiayi3 (1. College of Hydrology and Water Resources, Hohai University, Nanjing 210098, China;2.PowerChinaHuadongEngineeringCorporationLimited,Hangzhou310014,China;3.CollegeofWaterConservancyandHydropowerEngineering,HohaiUniversity,Nanjing210098,China) Abstract:Different combinations of meteorological factors, including monthly maximum temperature, monthly minimum temperature, monthly average temperature, average wind speed, sunshine duration, and relative humidity were used as the input data, the results calculated by the FAO Penman-Monteith equation were used as the calibration values, and a PSO-LSSVM model based on the least squares support vector machine (LSSVM) and particle swarm optimization (PSO) was established for prediction of ET0. Meteorological data from the Habahe Meteorological Station in the Irtysh River Basin over the period from 1986 to 2013 were used to train and test the model, and the results calculated by the PSO-LSSVM model were compared with those calculated by other commonly used ET0 calculation formulas. The results show that the PSO-LSSVM model can reflect the non-linear relationships between ET0 and the meteorological factors well, and that temperature is the most important factor that influences the accuracy of simulation. However, as the number of meteorological factors decreases, the accuracy of simulation will decrease. When the calculation is based on radiation and temperature conditions, the PSO-LSSVM model has higher accuracy than the Priestley-Taylor and Hargreaves-Samani equations. The PSO-LSSVM model, with multi-factor quantitative indicators, is both precise and practical, providing scientific references for ET0 study in areas that lack data. Key words:ET0; meteorological factors; PSO; LSSVM; Irtysh River Basin

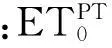

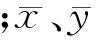
3 结果与分析
4 结 论
