河川径流情势主成分分析

张代青,于国荣

(昆明理工大学电力工程学院, 云南 昆明　650500)



河川径流情势主成分分析

张代青,于国荣

(昆明理工大学电力工程学院, 云南 昆明650500)

摘要：为了获得正确、可靠的河川径流情势,有效开发利用河流水能资源,以抚河流域为案例,分析了抚河12个水文站的日均流量、最小日平均流量、最大(小)月平均流量、基流指数、小于或等于年均流量5%的持续天数、大于或等于90 d的日均流量、日均流量标准偏差、年均流量变异系数等10个变量的径流样本主成分,计算了主成分的贡献率、累计贡献率、得分和样本综合得分,评价了抚河干支流径流情势。结果表明:第一主成分反映河川径流的阈值变幅、离散程度和对称状况,第二主成分反映河川径流的基流指数和变异系数,这2个主成分的贡献率依次降低。这些研究成果旨在为河流管理部门了解不同干支流河川径流情势、规划流域水能资源开发方案和维持河流良好水环境等提供技术支持和可靠的数据支撑。

关键词：主成分分析; 径流情势; 抚河流域

河川径流是流域水循环的基本环节,是可供人类长期开发利用的淡水资源[1]。为了合理开发和高效利用河川径流,在工程规划、设计、管理和科研阶段,需要进行河川径流计算,以量化河川径流情势,为确定工程设计规模、确保工程顺利施工、维护工程运行安全、获取工程运营效益和保护流域生态环境等,提供设计或实际代表年径流过程等径流数据。对于长期实测径流资料,可直接采用长系列操作法、设计代表年法和实际代表年法等计算设计年径流及其年内分配过程;对于短期实测径流资料甚至缺乏径流资料,采用参数等值线图法、水文比拟法和经验公式法等间接推求设计年径流及其年内分配过程[2]。但在实际应用中,往往由于许多中小型流域干支流的设计代表站或者可参证站只有断断续续的几年实测径流资料甚至根本没有资料,导致采用参数等值线图法、水文比拟法和经验公式法预估河川径流情势精度太低,或者根本无法预估河川径流情势,这将直接影响中小型流域的水资源开发和利用。为了解决这类实际问题,笔者尝试探讨一种理论技术方法,旨在从宏观角度分析计算和综合评价河川径流情势。

所谓河川径流,是指汇集地表和地下而进入河道的水流,包括地表径流和地下径流。河川径流情势是指河川径流各水文要素随时间、空间的变化情况,其水文要素包括水位、流速和流量等,变化情况包括河川径流的年际变化、年内分配、洪水和枯水过程。根据我国河流丰、平、枯水期的径流变化特征及国外研究成果[3],影响河川年均径流情势的主要因素包括年均日流量、年最大(小)日流量、年均日流量与流域面积之比、年最大(小)月平均流量、基流指数、基流分布指数、流域面积、河网密度、小于或等于年均流量5%的天数、小于或等于年均流量5%的最长持续天数、大于或等于90 d的日流量、年均日流量的标准偏差、年均流量的变异系数、缺水量、最大供水率、地表开发利用率等42个指标,详见参考文献[3]。

主成分分析法(principal components analysis,PCA)[4]是利用降维思想简化数据集的经典统计技术方法,该方法通过保留数据集的低阶主成分,忽略高阶主成分的方式,将数据集的最重要方面保留在低阶成分中,以达到减少数据集维数,同时保持数据集中对方差贡献最大特征的目的。实际应用中,发现其中许多指标具有交叉重叠现象,意味着可能只需应用几个能反映径流情势综合信息的新自变量即可解决问题,因此可以尝试应用主成分分析法来分析计算和综合评价河川径流情势。目前,主成分分析法已广泛应用于许多领域的数据分析及模型建立的综合评价中[5-10],取得的研究成果证明了该方法具有很好的应用前景。基于以上研究背景,笔者在介绍主成分分析法的基础上,尝试应用主成分分析法计算和综合评价河川径流情势,旨在为解决这类传统的水文分析及水文计算问题寻找一种简单明了的新途径。

1　主成分分析法

1.1基本原理

主成分分析法由卡尔·皮尔逊[11]于1901年提出,也称主分量分析法,是一种利用降维技术减少变量个数的统计分析方法,通常是将涉及太多变量的问题转化为少数几个综合变量的问题,从而降低分析问题的复杂性和减少统计分析的工作量。其基本原理可表述如下:

假定有n个样本,每个样本共有p个变量,构成一个n×p阶的数据矩阵X为

(1)

当p较大时,在p维空间中分析问题较复杂。为了减少问题的复杂性,利用降维技术以较少的几个综合变量代替原来较多的p个变量,并且使这些较少的几个综合变量既能尽量多地反映原来较多变量所反映的信息,又彼此相互独立。为此可给出定义:对n个样本中的任一样本,记(x1,x2,…,xp)为原变量,(y1,y2,…,ym)(m≤p)为新变量,且原变量与新变量有下列函数关系:

(2)

式中,系数zij(i=1,2,…,m;j=1,2,…,p)称为新变量(y1,y2,…,ym)上的载荷,其确定原则为:①yi与yj(i≠j;i,j=1,2,…,m)相互无关;②y1为x1,x2,…,xp的一切线性组合中方差最大者,y2为与y1不相关的x1,x2,…,xp的所有线性组合中方差最大者,依此类推,ym为与y1,y2,…,ym-1都不相关的x1,x2,…,xp的所有线性组合中方差最大者。新变量(y1,y2,…,ym)分别称为原变量(x1,x2,…,xp)的第一,第二,…,第m主成分。

从以上分析可知,主成分分析的实质是确定原来变量xj(j=1,2,…,p)在m个主成分yi(i=1,2,…,m)上的载荷zij,且载荷zij分别是相关矩阵X的m个较大的特征值所对应的特征向量,这可从数学上得到证明。

1.2计算步骤

根据主成分分析法的基本原理,利用计算机语言编程或者应用SPSS软件可实现主成分分析。计算步骤如下:

步骤1:计算相关系数矩阵

首先计算相关系数矩阵R,由原变量xi(i=1,2,…,p)与xj(j=1,2,…,p)两向量之间的相关系数rij(i,j=1,2,…,p)组成,rij的计算公式为

(3)

根据式(3)及两变量之间的相关系数的关系,显然有rij=rji,计算的相关系数rij即得相关系数矩阵R为

(4)

步骤2:计算特征值与特征向量

步骤3:计算贡献率及累计贡献率

主成分贡献率ei是指主成分的方差占总方差的比率,反映了原来p个变量有多大的信息和多大的综合能力,也表示了各主成分的相对重要性。主成分的贡献率可用特征值的相对比率来计算,计算公式为

(5)

(6)

在实际应用中,应该提取主成分的个数、主成分的累计贡献率的取值一般遵守各主成分对应的特征值大于1且主成分累计贡献率大于或等于85%的提取原则,最常见的情况是主成分提取个数为2～4个。

步骤4:计算主成分载荷及样本得分

主成分载荷是反映主成分yi(i=1,2,…,m)与原变量xj(j=1,2,…,p)之间相互关联程度的系数,实际是指式(2)中的zij,计算公式为

(7)

首先计算n个样本中各主成分yi(i=1,2,…,m)的得分,主成分得分Fij(i=1,2,…,n;j=1,2,…,p)等于其载荷与原变量xj(j=1,2,…,p)中心化后的值的乘积之和;然后根据计算的各主成分得分Fij计算各样本的综合得分Fi(i=1,2,…,n),Fi为每个主成分得分与其对应的方差贡献率的乘积之和,通过比较各样本综合得分的大小,可对各样本进行排序和主次地位评价。Fi的计算公式为

(8)

2　实例研究

抚河是江西省第二大河,是鄱阳湖水系的主要河流之一,是抚州地区的生命河。抚河流域(115°30′E～117°10′E,26°30′N～28°37′N)位于江西省东部,南北长240 km,东西平均宽70 km,流域面积15 811 km2。该流域由干流和8条主要支流组成,干流全长348 km,水系分布及站点位置见图1。

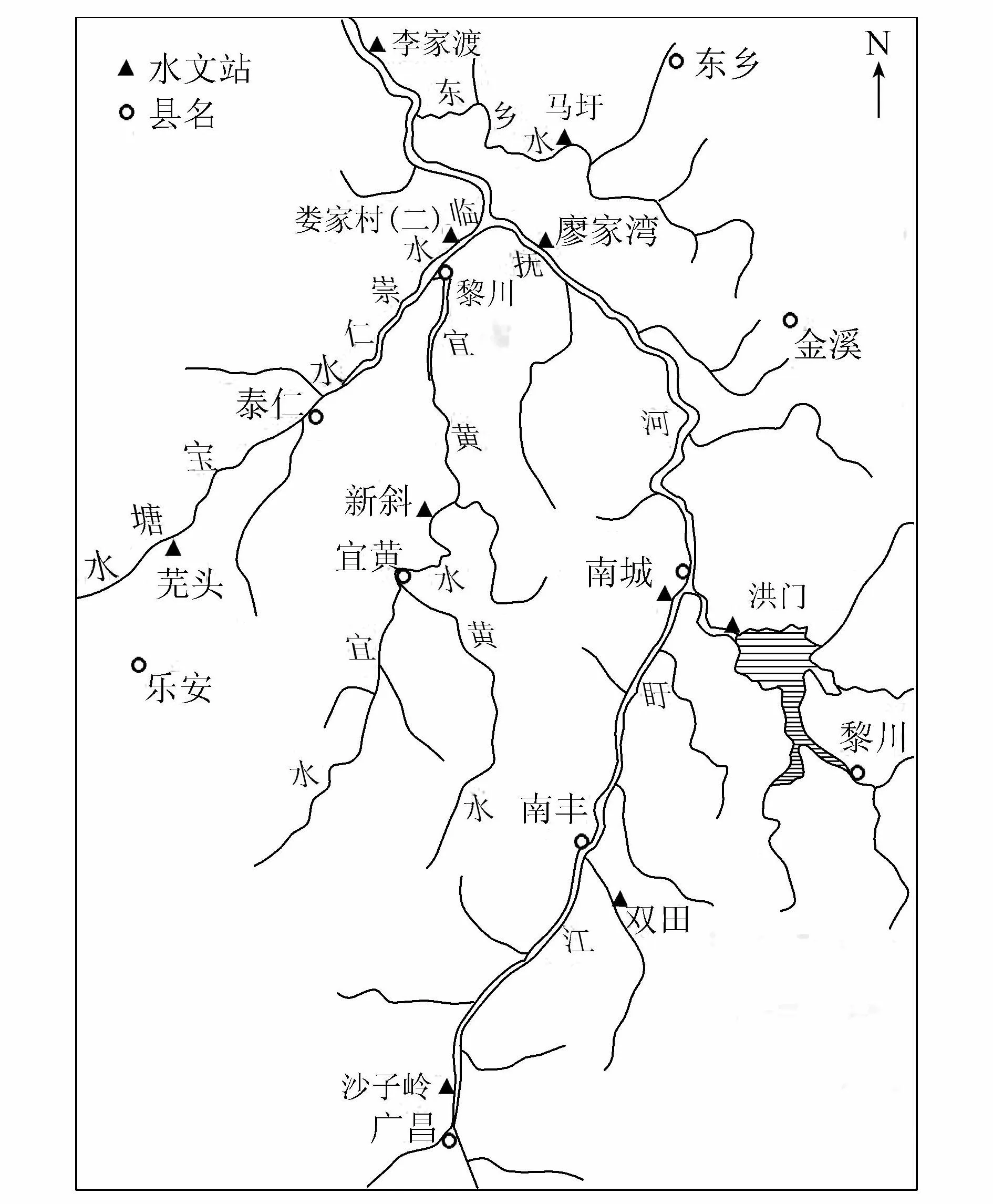
图1　抚河流域水系分布

抚河流域水资源较丰富,但随着流域经济的快速发展、人口的急剧增加和人类活动的日益加剧,生命、生活、生态和生产需水之间冲突日益尖锐。为缓解这些冲突,江西省已开展一些水量分配研究[12-14],为了有效实施各种水量分配方案,应该首先了解和熟悉该流域的干支流径流情势,否则,水量分配方案将成为“巧妇难为无米之炊”。根据抚河干支流的相关实测数据,应用主成分分析法探讨其河川径流情势。

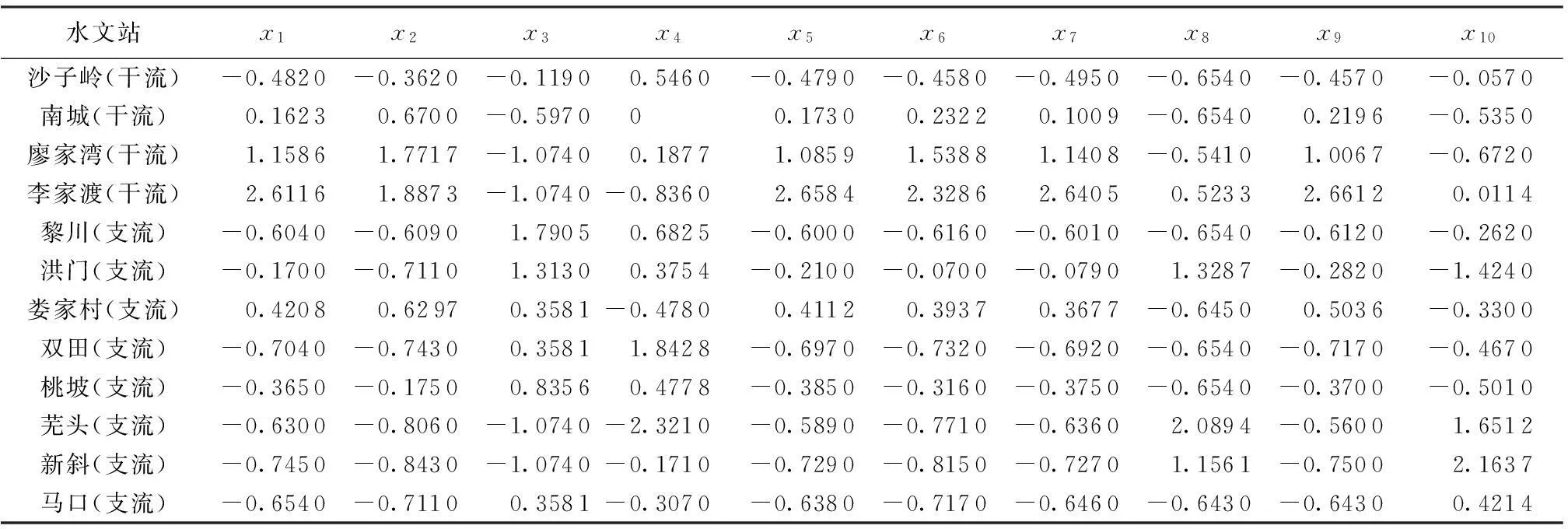
表1　抚河流域干支流12个水文站对应的10个指标的标准化矩阵

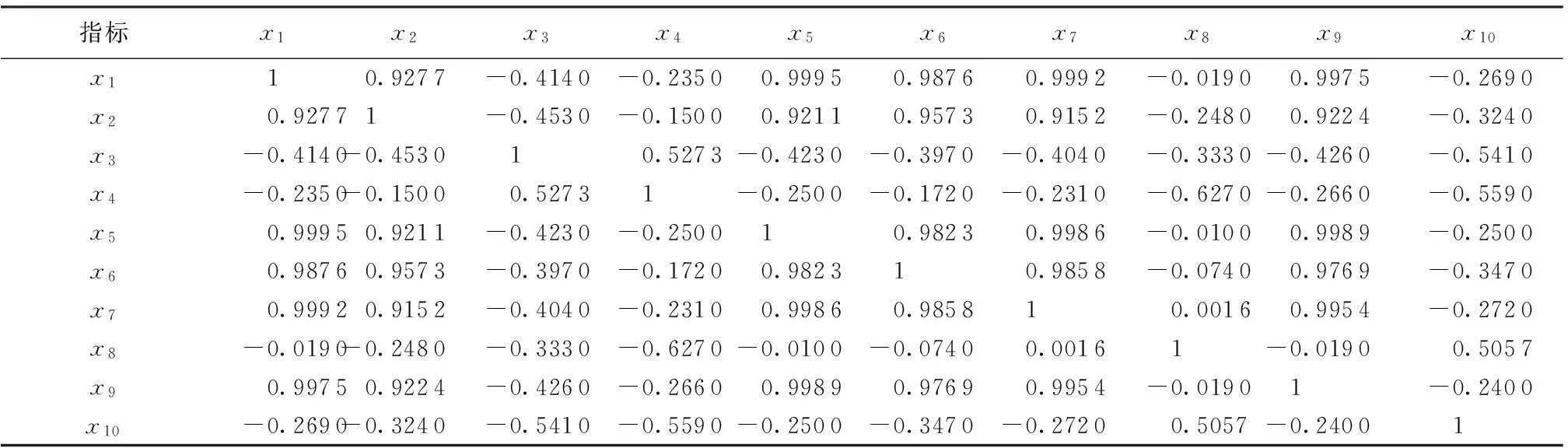
表2　相关系数矩阵

表3　特征值

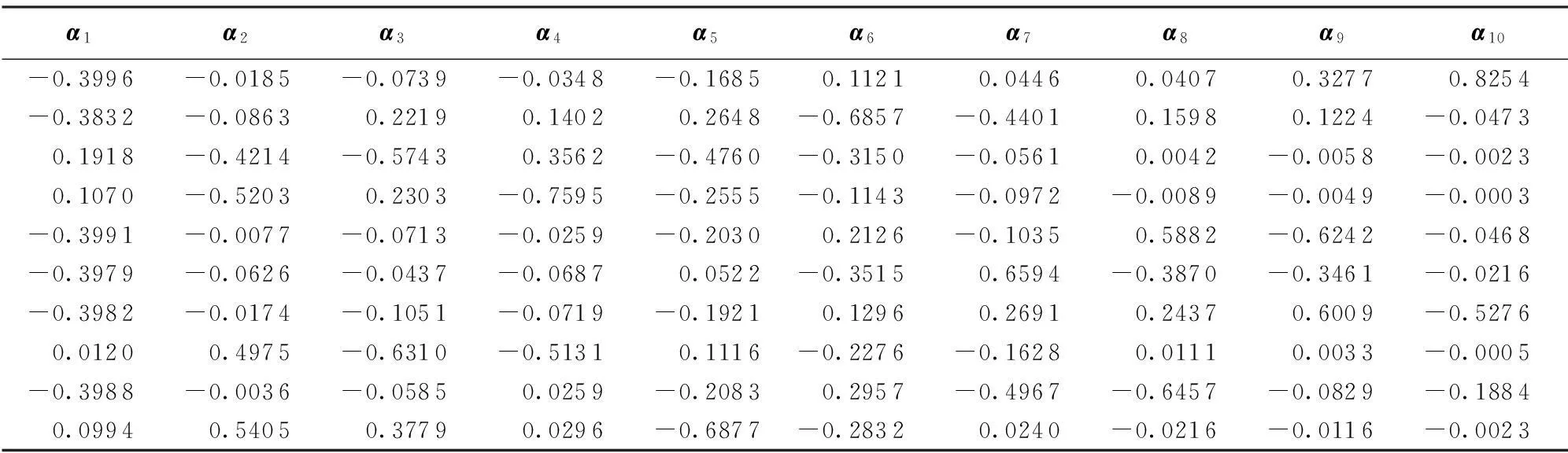
表4　特征向量

2.1资料预处理

选取抚河流域干支流12个水文站10年的日平均实测流量、集水面积等数据为分析资料,求出各水文站的日平均流量(x1)、最小日平均流量(x2)、日平均流量/集水面积(x3)、最小月平均流量/年平均流量(x4)、最大月平均流量(x5)、最小月平均流量(x6)、大于或等于90 d的日平均流量(x7)、小于或等于年均流量5%的最长持续天数(x8)、日平均流量的标准偏差(x9)、年平均流量的变异系数(x10)等引言中提出的42个指标,应用主成分分析法初步识别其主成分,按照其重要性程度拟定10个指标,利用Matlab程序实现主成分分析,10个指标的标准化矩阵见表1。

2.2主成分分析

根据公式(4)～(6),计算相关系数矩阵见表2,求解相关系数矩阵构成的特征方程得特征值和特征向量见表3～4,计算主成分贡献率及累计贡献率见表5。

由表5可知,第一、第二主成分的累计贡献率已高达87.32%,故只需求出第一、第二主成分y1、y2即可。根据计算的特征值λ1、λ2及对应的特征向量α1、α2,应用式(7)～(8)计算主成分y1、y2的载荷见表6,计算样本综合得分见表7。

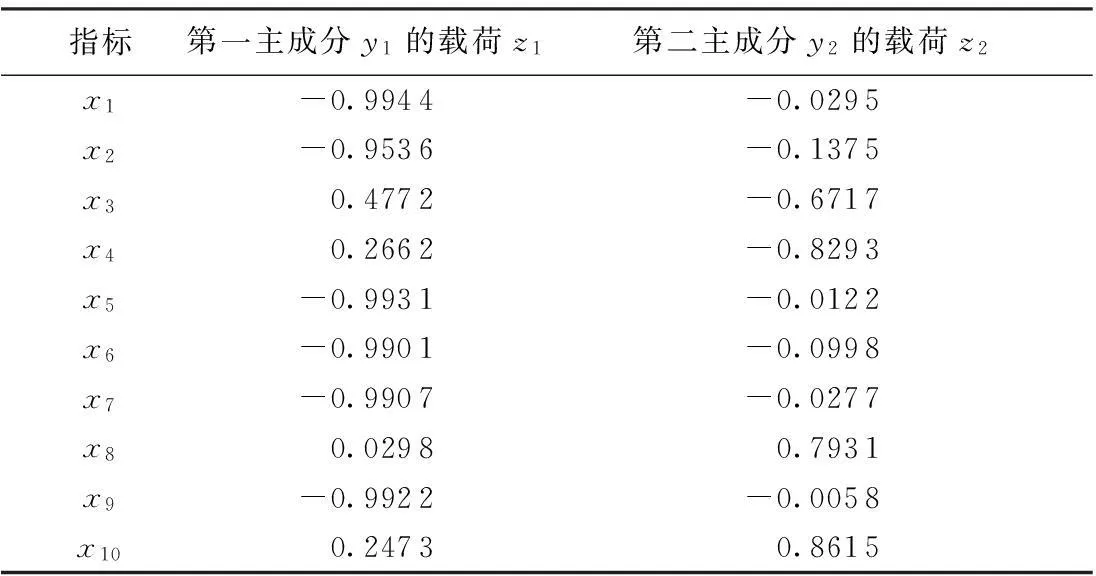
表6　第一、二主成分载荷计算结果

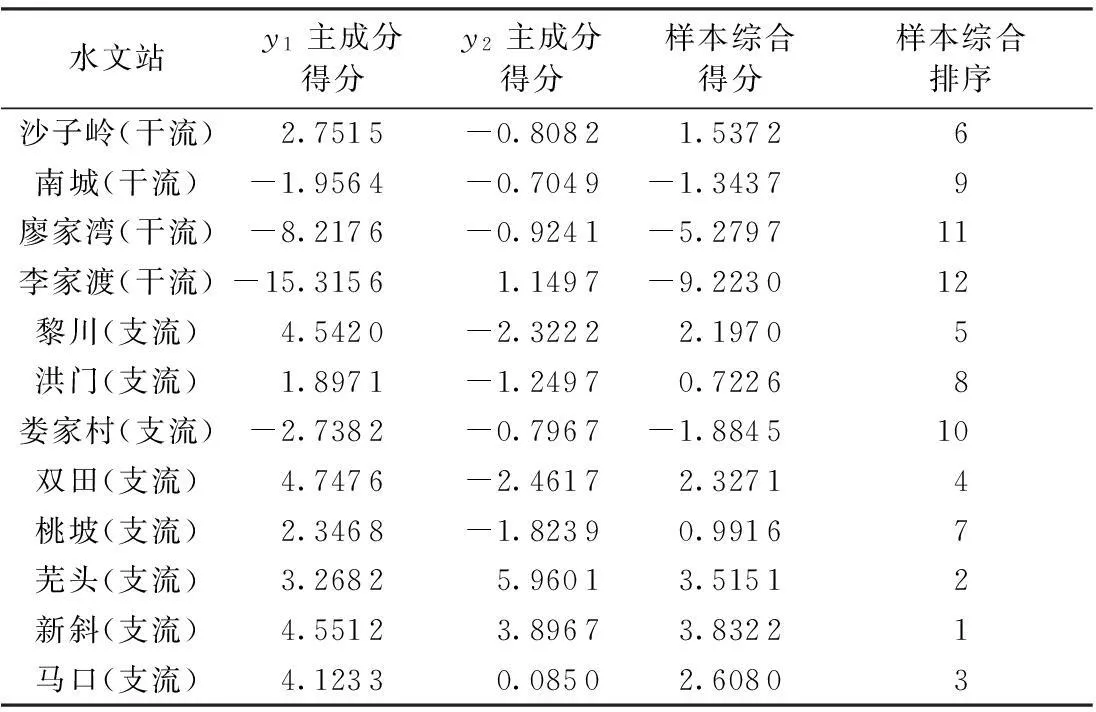
表7　主成分及样本综合得分与排序

2.3结果与分析

根据表5～7,以上主成分分析结果如下:

a. 抚河流域干支流径流的10个指标反映的信息,基本上可用2个主成分代替。这是因为第一主成分(y1)包含的信息量约占61.91%,第二主成分(y2)包含的信息量约占25.41%,两个主成分包含的信息量约占87.32%,已超过主成分分析法公认采用的85%。

b. 第一主成分与x1、x2、x5、x6、x7、x9呈现出较强的负相关,与x3、x4、x10呈现出较弱的正相关,与x8呈现出最弱的正相关,说明第一主成分是河川径流阈值变幅、离散和对称状况的综合体现。从第一主成分的得分及其排序来看,排在前5位的都是支流,且先后顺序依次为双田、新斜、黎川、马口和芜头。这表明,这5条支流的径流情势变化比较剧烈,即在最小供水量、供水保证率、供水持续时间等方面表现为比较不稳定,其中双田水文站所在支流最不稳定。

c. 第二主成分与x8、x10呈现出较强的正相关,与x3、x4呈现出较强的负相关,与x1、x2、x5、x6、x7、x9呈现出很弱的负相关,说明第二主成分主要反映了该流域干支流径流的基流指数和变异系数。从第二主成分的得分及其排序来看,排在前5位的干支流依次为芜头、新斜、李家渡、马口和南城。这表明,这5条干支流的基流较稳定、年内径流变异性较小,绝对来水量按时间分布较均匀,其中芜头水文站所在支流表现最佳。

d. 从表7可知,在所选取的12个水文站中,样本综合得分从高到低依次排序为新斜、芜头、马口、双田、黎川、沙子岭、桃坡、洪门、南城、娄家村、廖家湾和李家渡。即从该流域多年径流情势来看,新斜水文站所在支流表现为最不稳定,其次为芜头,再次为马口,最稳定为所在干流的李家渡水文站,这与新斜站位于支流上游导致来水不稳定、李家渡站位于干流出口导致来水最稳定的实际情况一致。

3　结　论

a. 主成分分析法用于河川径流情势分析,既能正确识别原来太多变量中的主要成分,又能高度浓缩原来太多变量中的综合信息,还能反映各主成分与原变量之间相关性的正、负和强、弱,具有有效识别主要成分和高度概括综合信息等优点。

b. 主成分分析法用于河川径流情势分析,通过选用少数几个主成分代替流域径流状况的多个指标,从定量角度描述河川径流的情势,综合评价河川径流的稳定性及流域综合供水的稳定程度,具有简化计算、简单明了等优点。

c. 主成分分析法用于河川径流情势评价,既能正确评价不同干支流样本径流的离散性、对称性和稳定性等,又能为整个流域干支流径流情势的变化特征进行优劣排序,可为河流管理部门合理决策河流水能资源开发方案提供技术支持和方法参考。

参考文献：

[1] 王亮.滦河流域内蒙段径流插补预测分析及径流变化影响评价研究[D].呼和浩特: 内蒙古农业大学,2011.

[2] 詹道江,徐向阳,陈元芳.工程水文学[M].北京: 中国水利水电出版社,2010:165-182.

[3] ALCAZAR J,PALAU A,VEGA-GARCLA C.A neural net model for environmental flow estimation at the Ebro River Basin,Spain[J].Journal of Hydrology,2008,349(1):44-55.

[4] 赵海霞,武建.浅析主成分分析方法[J].科技信息,2009(2): 87.(ZHAO Haixia,WU Jian.Brif analysis on the principal component analysis method[J].Journal of Science & Technology Information,2009(2): 87.(in Chinese))

[5] 童其慧.主成分分析方法在指标综合评价中的应用[J].北京理工大学学报(社会科学版),2002,4(1): 59-61.(TONG Qihui.The application of primary element analyzing methods in the index synthetic evaluation [J].Journal of Beijing Institute of Technology(Social Sciences Edition),2002,4 (1): 59-61.(in Chinese))

[6] 盛周君,孙世群,王京城.基于主成分分析的河流水环境质量评价研究[J].环境科学与管理,2007,32(12): 172-175.(SHENG Zhoujun,SUN Shiqun,WANG Jingcheng.Comprehensive evaluation of river water environmental quality based on principal component analysis[J].Journal of Environmental Science & Management,2007,32(12): 172-175.(in Chinese))

[7] 顾大环,赵建强.主成分分析法在江苏省工业经济效益评价中的应用[J].徐州教育学院学报,2008,23(3): 183-185.(GU Dahuan,ZHAO Jianqiang.The application of principal component analysis method in industrial economic benefit evaluation of Jiangsu Province[J].Journal of Xuzhou Education College,2008,23 (3): 183-185.(in Chinese))

[8] 赵磊,李继海,朱大洲,等.5种鹿茸营养成分的主成分分析[J].光谱学与光谱分析,2010,30(9): 2571-2575.(ZHAO Lei,LI Jihai,ZHU Dazhou,et al.Principal component analysis of nutrients in five kinds of velvet antler [J].Spectroscopy & Spectral Analysis,2010,30 (9): 2571-2575.(in Chinese))

[9] 欧建锋,叶健,程吉林.主成分分析法在江苏水利现代化评价中的应用[J].人民长江,2010,41(2): 97-100.(OU Jianfeng,YE Jian,CHENG Jilin.Application of main component analysis method in comprehensive evaluation for water conservancy modernization in Jiangsu Province[J].Yangtze River,2010,41 (2): 97-100.(in Chinese))

[10] 吕王勇,陈美香,王波.基于主成分的区域水资源与社会经济的协调度评价[J].水资源与水工程学报,2011,22(1): 182-125.(LYU Wangyong,CHEN Meixiang,WANG Bo.Coordination evaluation between regional water resources and socio-economic based on principal component [J].Journal of Water Resources and Water Engineering,2011,22 (1): 182-125.(in Chinese))

[11] 谭芳,崔远来,王建漳.灌溉水利用率影响因素的主成分分析: 以漳河灌区为例[J].中国农村水利水电,2009(2): 70-73.(TAN Fang,CUI Yuanlai,WANG Jianzhang.Impact factors of irrigation water use efficiency based on principal component analysis case from Zhang River Irrigation District [J].China Rural Water and Hydropower,2009(2): 70-73.(in Chinese))

[12] 杨永生,许新发,祝水贵,等.江西抚河流域水量分配方案研究[J].中国水利,2006(9): 19-22.(YANG Yongsheng,XU Xinfa,ZHU Shuigui,et al.Water allocation study on Fu River Basin of Jiangxi[J].China Water Resources,2006(9):19-22.(in Chinese))

[13] 杨永生,张戴军.抚河流域水量分配原则及方法解析[J].江西水利科技,2006,32(3): 169-172.(YANG Yongsheng,ZHANG Daijun.Discussion of the distribution principle and the method of the water quantity about Fuhe River basin[J].Jiangxi Hydraulic Science & Technology,2006,32 (3): 169-172.(in Chinese))

[14] 桂发亮,胡铁松,许新发.抚河流域区域间的水权初始分配[J].武汉大学学报(工学版),2007,40(3): 27-30.(GUI Faliang,HU Tiesong,XU Xinfa.Inter-regional water right distribution of Fuhe River in China [J].Engineering Journal of Wuhan University,2007,40 (3): 27-30.(in Chinese))

DOI：10.3880/j.issn.1004-6933.2016.04.006

作者简介：张代青(1974—)，男，讲师，博士，主要从事水资源保护、规划与管理研究。E-mail:dqzhang2014@126.com

中图分类号：TV213

文献标志码：A

文章编号：1004-6933(2016)04-0039-06

(收稿日期：2015-06-03编辑：王芳)

Principal component analysis of runoff regimes of rivers

ZHANG Daiqing, YU Guorong

(Faculty of Electric Power Engineering, Kunming University of Science and Technology, Kunming 650500, China)

Abstract：In order to obtain correct and reliable runoff regimes, and to effectively develop and utilize hydropower resources of rivers, using the Fuhe River Basin as an example, we analyzed the principal components involving ten variables of runoff samples from 12 hydrological stations on the Fuhe River. The variables included daily mean flow, minimum daily mean flow, maximum and minimum monthly mean flows, base flow index, number of days during which the streamflow is equal to or lower than 5% of annual mean flow, daily mean flow for a period of 90 days or one exceeding 90 days, standard deviation of daily mean flow, and coefficient of variation of the annual mean flow. We calculated the contribution rates of the principal components, the cumulative contribution rates, and scores of samples and their comprehensive scores, and evaluated the runoff regimes of the main stream and tributaries of the river. The results show that the first principal component reflects the threshold value range of runoff, discrete degree, and symmetry conditions; the second principal component reflects the base flow index and the coefficient of variation of runoff, and the contribution rates of the two principal components decrease successively. These research results can provide river management departments with technical support and a reliable data basis for understanding runoff regimes of different main streams and tributaries, planning programs for development of hydropower resources in river basins, and maintaining a healthy water environment for rivers.

Key words：principal component analysis; runoff regime; Fuhe River Basin