拓扑一致降标与性质(gω)
2016-08-13戴磊
戴 磊
(渭南师范学院 数理学院,陕西 渭南 714099)
拓扑一致降标与性质(gω)
戴磊
(渭南师范学院 数理学院,陕西 渭南 714099)
摘要:Banach空间算子T满足性质(gω)当且仅当T在它的所有孤立的特征值处有n≥d的拓扑一致降标且T*在T的上半B-Weyl谱的补集上具有单值扩张性质。另外,利用所得结论证明了代数paranormal算子和初等算子满足性质(gω)。
关键词:性质(gω);拓扑一致降标;代数paranormal算子;初等算子
0 引言
对线性算子谱理论的研究一直是算子理论中一个重要课题和热门分支,Weyl型定理是谱理论中一个比较活跃的研究方向,而性质(gω)是Weyl型定理变化性质之一。近年来关于性质(gω)的研究有许多,例如文献[1-2]利用单值扩张性质分别研究了算子及其摄动的性质(gω);文献[3]研究了性质(gω)与Weyl型定理之间的关系;文献[4]利用变化的本性逼近点谱研究了算子的性质(gω);文献[5]利用一致Fredholm指标性质研究了算子的性质(gω)。本文主要利用拓扑一致降标给出了Banach空间中有界线性算子T满足性质(gω)的一个等价刻画,然后将所得结果应用到了初等算子和代数paranormal算子上。
1 预备知识
本文中,X表示无限维复Banach空间,B(X)表示X上的有界线性算子代数。称算子T∈B(X)为一个上半Fredholm算子,若R(T)闭且n(T)=dim(N(T))<;若d(T)=dim(X/R(T))<, 则称T为一个下半Fredholm算子。算子T∈B(X)称为Fredholm算子,若n(T)和d(T)都有限。算子T的指标ind(T)定义为ind(T)=n(T)-d(T)。指标为0的Fredholm算子称为Weyl算子;指标小于等于0的上半Fredholm算子称为上半Weyl算子;指标大于等于0的下半Fredholm算子称为下半Weyl算子。算子T的升标asc(T)为满足 N(Tn)=N(Tn+1)的最小的非负整数,若这样的整数不存在,则记asc(T)=;而算子T的降标des(T)为满足R(Tn)=R(Tn+1)的最小的非负整数,同样,当这样的整数不存在时,记des(T)=。如果T的升标和降标均有限,则它们一定相等[6],此时称T为 Drazin 可逆的。记T的Weyl 谱、本性逼近点谱、Drazin 谱分别定义如下:
σw(T)={λ∈C:T-λ不为Weyl普及算子};
σea(T)={λ∈C:T-λ不为上半Weyl算子};
σD(T)={λ∈C:T-λ不为Drazin可逆}。

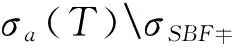
称T在λ0处有单值扩张性质,如果任给λ0的开邻域U(λ0),f为U(λ0)→X上的解析函数且满足(T-λI)f(λ)=0(λ∈U(λ0)),则恒有f≡0。如果T在任意点λ∈C都有单值扩张性质,则称T有单值扩张性质。显然,若intσp(T)=∅,则T有单值扩张性质,于是T在任意λ∈isoσ(T)或λ∈Cσa(T)处都有单值扩张性质。
2 主要结论
定义1[7]设T∈B(X),如果存在d∈N,使得对任意的n≥d,都有R(T)+N(Tn)=R(T)+N(Td),则称T有n≥d的一致降标;如果R(T)+N(Td)还是闭集,则称T有n≥d的拓扑一致降标。
由文献[8]知,当T是半B-Fredholm算子时,T有n≥d的拓扑一致降标。如果T有n≥d的拓扑一致降标,根据文献[9]中推论4.9可知T有如下性质:
性质1设T∈B(X)且设λ∈isoσ(T),如果T-λI有n≥d的拓扑一致降标,则λ是T的一个极点。
下面记Π(T)为T的谱集中所有极点的全体,E(T)为T的谱集中孤立的特征值全体,显然Π(T)⊆E(T)。
性质2T在λ∈E(T)处有n≥d的拓扑一致降标当且仅当E(T)=Π(T)。
证明如果E(T)=Π(T),则任给λ∈E(T),都存在p≥1,使得
X=N((T-λI)p)⊕R((T-λI)p)。
根据定义易知T在λ处有n≥d的拓扑一致降标。反之利用性质1可知。
如果T*有单值扩张性质,则T有性质(gb)[1]。
另外,如果T在λ∈E(T)处有n≥d的拓扑一致降标,则T有性质(gω)。
下面定理说明T*的单值扩张性质假设可减弱到集合上半B-Weyl预解集上。
定理1设T∈B(X),则T满足性质(gω)当且仅当下列叙述成立:
(1)T在集合E(T)上有n≥d的拓扑一致降标;


推论1假设T在任意λ∈isoσ(T)处都有n≥d的拓扑一致降标,
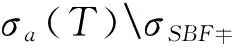
证明根据定理1,(1) 显然成立,只需证(2)。

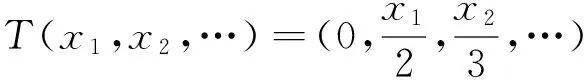
下面设H(σ(T))表示在σ(T)的某一邻域内解析且在σ(T)的任一分支上不为常值的复值解析函数全体。
定理2假设T在任意λ∈isoσ(T)处都有n≥d的拓扑一致降标,
(1)如果T*有单值扩张性质,则任给f∈H(σ(T)),有f(T)都满足性质(gω);
(2)如果T有单值扩张性质,则任给f∈H(σ(T)),有f(T*)都满足性质(gω)。
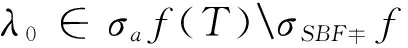
f(T)-λI=(T-λ1I)n1(T-λ2I)n2…(T-λkI)nkg(T),
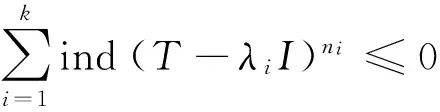
N(f(T)-λI)⊆N(f(T)-λI)∩R(f(T)-λI)={0}[9]。
于是f(T)-λI可逆,从而λ0∈isoσ(f(T))。由性质2知λ0∈Π(f(T)),则λ0∈E(f(T))。反之,设μ0∈E(f(T)),且设f(T)-μ0I=(T-μ1I)n1(T-μ2I)n2…(T-μkI)nkg(T),其中:μi≠μj(i≠j),g(T)可逆。

(2)根据推论1(2)的证明过程可知,T*在任意λ∈isoσ(T*)处都有n≥d的拓扑一致降标。如果T有单值扩张性质,则由类似于(1)的证明可知,任给f∈H(σ(T)),f(T*)都满足性质(gω)。
3 应用
称T为normaloid算子,如果对任意的λ∈C,都有算子T的谱半径r(T)=‖T-λI‖。如果任给λ∈C,T-λI都是normaloid算子,则称T是transaloid算子。由文献[10]知,若T是transloid算子,则任给λ∈C,H0(T-λI)=N(T-λI)。记
H(p)={T∈B(X): 任给λ∈C,都存在p≥1,使得H0(T-λI)=N[(T-λI)p]},
则transaloid算子⊆H(1)⊆H(p)。H(p)类算子涉及比较广泛,它包括Banach空间中的广义scalar算子、subscalar算子、totally paranormal算子及Hilbert空间中的hyponomal算子、p-hyponormal (0 X=H0(T-λI)⊕K(T-λI) =N[(T-λI)p]⊕K(T-λI) ⟹R[(T-λI)p]=K(T-λI) ⟹X=N[(T-λI)p]⊕R[(T-λI)p]。 由拓扑一致降标的定义知,如果T∈H(p),则任给λ∈isoσ(T),均有,T有n≥d的拓扑一致降标。 推论2设T∈B(X), (1)若T∈H(p),则任给f∈H(σ(T)),有f(T*)都满足性质(gω); (2)若T*∈H(p),则任给f∈H(σ(T)),有f(T)都满足性质(gω)。 下设H为Hilbert空间,称T∈B(H)是paranormal算子,如果任给x∈H,‖x‖=1,‖Tx‖2≤‖T2x‖。如果存在非常值多项式p,使得p(T)是paranormal算子,则称T是代数paranormal算子。由定义易证 引理1(1) 若T∈B(H)是代数paranormal算子,则任给λ∈C,T-λI也是代数paranormal算子; (2)若T∈B(H)是代数paranormal算子,T(M)⊆M,则T|M也是代数paranormal算子。 引理2[11]设T∈B(H)是代数paranormal算子, (1)如果σ(T)={λ},则T=λI; (2)如果T是拟幂零算子,则它是幂零算子。 推论3设T∈B(H)是代数paranormal算子,则任给f∈H(σ(T)),f(T*)都满足性质(gω)。 证明因为T是代数paranormal算子,则存在非常值多项式p使得p(T)是paranormal算子。由于paranormal算子有单值扩张性质,则p(T)有单值扩张性质。因此T有单值扩张性质。 下证T在任意λ∈isoσ(T)处都有n≥d的拓扑一致降标。 设λ∈isoσ(T),利用谱投影可以把T表示为T=T1⊕T2,其中σ(T1)={λ},σ(T2)=σ(T){λ}。若λ=0,则T1是拟幂零的代数paranormal算子,由引理2(2)知T1是幂零算子。因此T是可逆算子与幂零算子的直和,于是T是B-Weyl算子[12]。故T在0处有拓扑一致降标。若λ≠0,由σ(T1)={λ}知σ(p(T1))=p(σ(T1))={p(λ)}。则p(T1)-p(λ)I是拟幂零算子。因为p(T1)是paranormal算子,则由引理2(2)知q(T1)=p(T1)-p(λ)I=0。因此T是代数paranormal算子,根据引理2知T1-λI是幂零算子。因为T-λI是可逆算子与幂零算子的直和,于是T1-λI是B-Weyl算子[12]。故T在λ处有n≥d拓扑一致降标。根据定理2(2)可知,任给f∈H(σ(T)),f(T*)都满足性质(gω)。 定义dTS为广义导子δTS(X)=TX-XS或初等算子ΔTS(X)=TXS-X,其中T,S*∈B(H)是hyponormal算子,即|T|2≤|T|2,|S*|2≤|S|2。根据文献[13]知,任给λ∈C,asc(dTS-λ)≤1且任给λ∈isoσ(dTS),H0(dTS-λ)=N(dTS-λ)。因此,dTS有单值扩张性质,且任给λ∈isoσ(dTS),dTS在λ处有n≥d拓扑一致降标。由定理2(2)可知 推论4任给f∈H(σ(T)),f(dTS*)都满足性质(gω)。 参考文献: [1] Berkani M, Sarih M, Zariouh H. Browder-type Theorems and SVEP[J].Mediterranean Journal of Mathematics,2011,8(3):399-409. [2] Amouch M, Berkani M. On the Property (gω)[J].Mediterranean Journal of Mathematics,2008,(3):371-378. [3] Amouch M. Polaroid Operators with SVEP and Perturbations of Property (gω)[J].Mediterranean Journal of Mathematics, 2009,6(4):461-470. [4] 戴磊,曹小红,孙晨辉. 广义(ω)性质的一个注记[J].数学学报,2010,(2):219-226. [5] 戴磊,张建华,曹小红,等.CFI算子和Weyl型定理(英文)[J].数学进展,2014,(4):590-598. [6] Lauren K, Neumann M. An introduction to local spectral theory[M].Oxford:Clarendon Press,2000. [7] Grabiner S. Uniform ascent and descent of bounded operaters[J]. Journal of the Mathematical Society of Japan,1982,34:317-337. [8] Finch J. The single valued extension property on a Banach space[J].Pacific Journal of Mathematics,1975,58:61-69. [9] Taylor A. Theorems on ascent, descent, nullity and defect of linear operator[J].Mathematische Annalen,1966,163:8-49. [10] Curto R E, Han Y M. Weyl’s theorem, a-Weyl’s theorem, and local spectral theory[J].Journal of the London Mathematical Society,2002,67(2):499-509. [11] Curto R E, Han Y M. Weyl’s Theorem for Algebraically Paranormal Operators[J].Integral Equations & Operator Theory,2003,47(3):307-314. [12] Berkani M. Index of B-Fredholm operators and generalization of a Weyl theorem[J].Proceedings of the American Mathematical Society,2002,130(6):1717-1724. [13] Duggal B P. Weyl’s theorem for a generalized derivation and an elementary operator[J].Matematicki Vesnik,2002,54(3):71-81. 【责任编辑牛怀岗】 中图分类号:O177.2 文献标志码:A 文章编号:1009-5128(2016)16-0009-05 收稿日期:2016-03-18 基金项目:国家自然科学基金资助项目:基于量子力学的算子谱理论问题研究(11501419);陕西省军民融合基金资助项目:与量子力学相关的算子谱论研究(15JMR20) 作者简介:戴磊(1983—),男,河南荥阳人,渭南师范学院数理学院副教授,理学博士,主要从事算子代数与算子理论研究。 Topological Uniform Descent and Property(gω) DAI Lei (School of Mathematics and Physics, Weinan Normal University, Weinan 714099, China) Abstract:A Banach space operator T satisfying property (gω) if and only if T has topological uniform descent for n≥dat all λ which are isolated eigenvalues of T and T*, and has the single-valued property in the complement of the upper B-Weyl spectrum of T. In addition, the results show that the property (gω) holds for algebraically paranormal operators and elementary operators. Key words:property(gω); topological uniform descent; algebraically paranormal operators; elementary operators 【自然科学基础理论研究】
