基于粒计算的概念格拓展模型
2016-08-13康向平苗夺谦
康向平, 苗夺谦
(1. 同济大学 电子与信息工程学院, 上海 201804;2. 同济大学 嵌入式系统与服务计算教育部重点实验室, 上海 201804)
基于粒计算的概念格拓展模型
康向平1,2, 苗夺谦1,2
(1. 同济大学 电子与信息工程学院, 上海 201804;2. 同济大学 嵌入式系统与服务计算教育部重点实验室, 上海 201804)
摘要:将粒计算融入到概念格研究中,结合相似度模型和概念格结构信息,提出一种基于粒计算的概念格拓展模型,其有助于扩展经典概念的内涵和外延,也有助于压缩概念的规模.该模型是概念格和粒计算融合研究的一次有益探索和尝试,同时对概念格拓展也不失为一种有效手段.
关键词:概念格; 粒计算; 关系粒; 粒化概念格
德国Wi11e教授于1982年提出了形式概念分析[1],即概念格理论,该理论是格序论的一个重要分支,具有良好的数学性质,主要用于概念的发现、排序和显示.在概念格构筑的体系中,概念、完备格结构、伽罗瓦连接等是核心要素.从内涵和外延2个不同角度对概念进行刻画和描述,有助于深化人们对现实世界中概念的概要认识和准确理解;完备格结构作为一种基于序关系建立起来的概念层次模型,直观地反映了概念之间的泛化/特化关系;伽罗瓦连接则是概念格体系的基石.概念格作为一种强有力的数据分析工具,受到了学者的广泛关注,其在基础理论[2-7]、格生成算法[8-9]、规则获取[10-14]、属性约简[15-16]等方面,以及在不同领域的应用[17-18]取得了大量的研究成果.近年来,许多学者系统研究了概念格与模糊集[19-21]、粗糙集[22-28]、神经网络[29]、概率论[30]、粒计算[31-33]等知识发现方法之间的联系,旨在探索复杂数据处理的新途径.这种多技术之间的渗透和交叉,有助于推动概念格向深层次和多元化方向发展.Burusco[21]将模糊集引入概念格,用于度量对象和属性之间的不确定性关系,有助于解决复杂问题中的模糊信息和不确定信息;Dias等[29]探讨了概念格和神经网络融合理论;Jiang等[30]将概率论引入到概念格中,提出了一种新的数据挖掘方法;Yao[28]将粗糙集中的上下近似思想引入到概念格中,探讨了概念格中的近似算子;Kang等[32]将粒计算引入概念格,提出了概念格在不同粒度下的知识获取模型,该模型为概念格构建和规则获取提供了统一的基于模糊粒化基的求解方法,不仅可以有效简化复杂的概念格结构和压缩庞大的概念规模,而且就决策规则集的完备性和无冗余性做了一些有益的尝试.关于概念格的最新相关研究成果,详见文献[34].
在经典概念格中,对于概念的刻画是精确的.然而,这种精确性在实际应用中可能存在一定的局限性,不利于人们从看似不相关的数据中发现一些有价值的信息.在此情况下,就需要考虑进一步拓展概念的内涵和外延,将概念“可能”包含的一些对象也纳入到其外延中.例如,在地震预测中,若一些测量结果符合地震的“大部分”特征而非“全部”特征时,专家一般提前判定地震可能会发生,而不是等到“全部”特征符合后再做出判定.此外,在一些大规模复杂的数据集中,概念的这种精确性通常会使知识获取过程淹没在一些不必要的细节中,并最终导致海量概念和复杂的格结构,不利于更好地从整体认识和理解问题.针对上述问题,本文尝试引入粒计算.粒计算以粒、粒度、粒推理等为核心要素,通过模拟人类思维方式在大规模复杂数据建模与分析中独特的优势,可以降低知识获取的“分辨率”,扩大知识度量的“尺度”,有助于人们对问题的宏观认识和理解.
目前,关于概念格与粒计算的融合研究还尚不多见[31-33],据此,本文将粒计算融入到概念格研究中,提出了粒化概念格和粒化概念.粒计算的引入不仅有助于扩展经典概念的内涵和外延,而且也有助于压缩概念的规模并简化复杂的格结构.
1 概念格简介
形式背景是一个三元组(G,M,I),其中G和M是非空有限集,I⊆G×M是一个从集合G到集合M的二元关系.表1是一个从超市采集的数据集,其中1,2,…,9表示顾客编号;a,b,…,e表示商品编号,若某位消费者购买了某种商品,则用“×”进行标记.
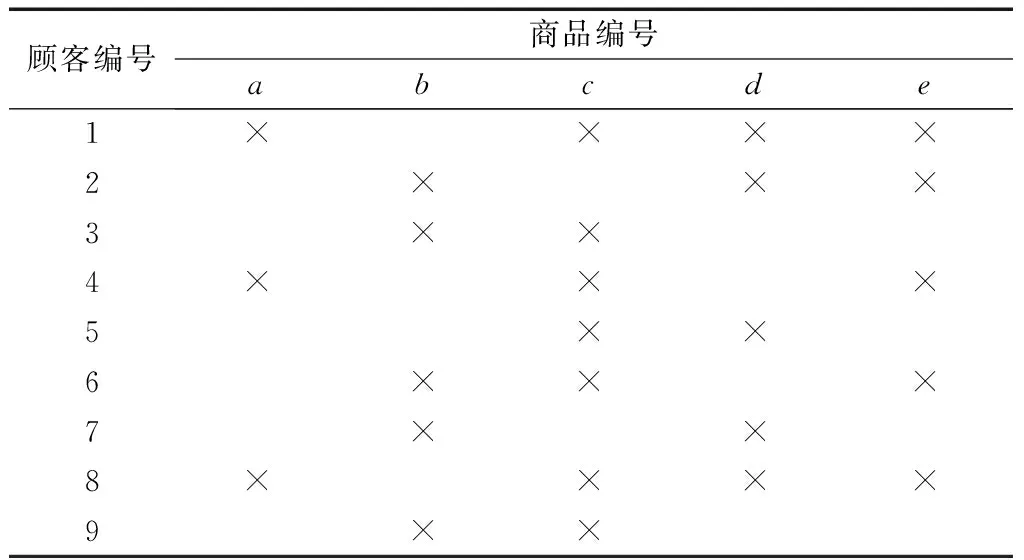
表1 一个典型的形式背景
定义1设K=(G,M,I)是一个形式背景,A⊆G,B⊆M.若A′=B且B′=A,则称(A,B)是一个概念,此时称A和B分别为概念的外延和内涵.其中,算子A′被描述为
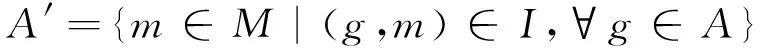
相应地,算子B′被定义为
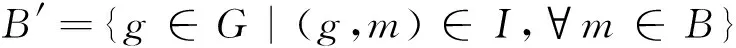
对于任意概念(A1,B1)和(A2,B2),它们之间的偏序关系定义为
事实上,(B(K),≤)是一个完备格,其中B(K)是一个由K中所有概念组成的集合.图1即是表1中的概念格.

图1 由表1生成的概念格
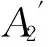
定义2设K=(G,M,I)是一个形式背景,对于任意g∈G,称γg为对象概念,即
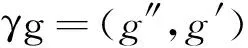
对于任意m∈M,称μm为属性概念,即
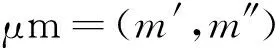
γ(G)表示由所有对象概念组成的集合,μ(M)表示由所有属性概念组成的集合.对象概念和属性概念作为概念格中的基础概念,扮演着重要角色.通常,图1也可以简化表示为图2,其中“m”代表μm,“g”代表γg.
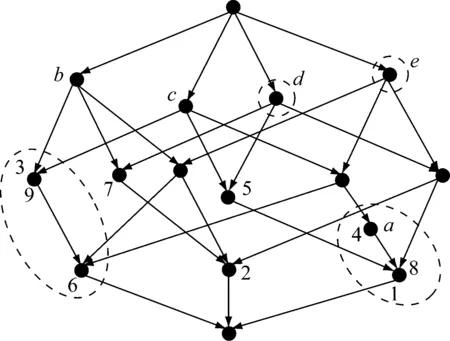
图2 图1的简化概念格
引理2在形式背景K=(G,M,I)中,设B⊆M,则
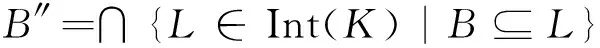
其中,Int(K)是一个由所有概念内涵组成的集合.
关于概念格的更详细介绍,请查阅文献 [2].
2 粒化形式背景
概念格的粒化本质上是形式背景的粒化,据此,本文探讨了形式背景中的对象粒和关系粒,并在此基础上构建了粒化形式背景.
2.1相似度模型和对象粒
在传统的相似度度量模型中,特征模型是最常见的度量模型之一.特征模型主要包含两大类,一类是基于公共特征集构造的对称性特征模型,例如
其中Bi和Bj分别是对象gi和gj的特征集.另一类是基于差异特征集构造的不对称性特征模型,例如:
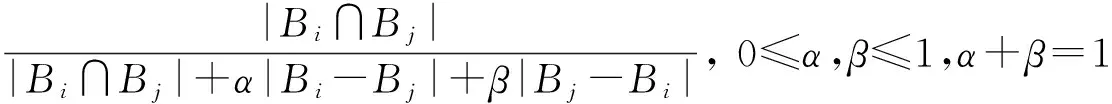
其中,Bi和Bj分别是对象gi和gj的特征集.该模型同时引入了共同特征集和差异特征集,相对于差异特征集,共同特征对于相似度的影响要更大一些.此外,参数α和β体现了2个不同的差异特征集Bi-Bj和Bj-Bi对于相似度的影响是不对称的.
本文研究的重点是对称相似度模型,详见定义3.
定义3在形式背景(G,M,I)中,设0≤σ≤1,对于任意gi、gj∈G,定义

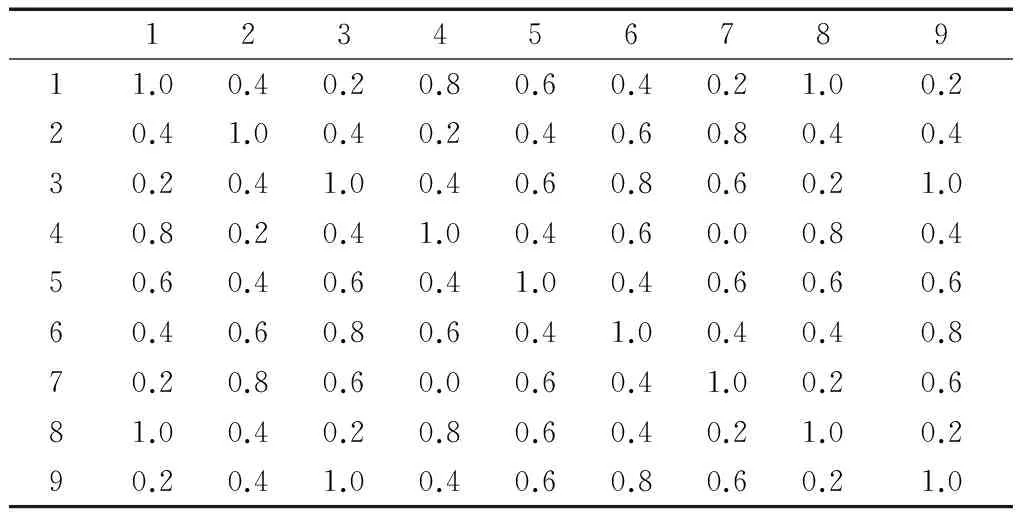
表2 模糊相似矩阵
定理1在形式背景(G,M,I)中,对于任意对象gi、gj∈G,有下述性质成立:
(1) 0≤ρ(gi,gj)≤1.

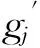
证明由ρ的定义即得性质(1)和(2)成立.
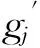
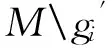
进而
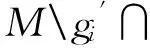
显然,结论ρ(gi,gj)≤ρ(x,y)成立.
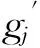
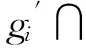
显然,有结论ρ(gi,gj)≤ρ(gi,z)成立.类似地,有ρ(gi,gj)≤ρ(gj,z)成立.证毕.
由上述定理可知,本文定义的相似度模型是合理的.事实上,依据该模型可以导出一个模糊相似关系矩阵
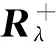
λ的值越小,相应G中的对象粒就越大.一个从表2导出的模糊等价矩阵如表3所示.在表3中,当λ=0.8时,有
其中,[1]=[4]=[8]={1,4,8},[2]=[7]={2,7},[3]=[6]=[9]={3,6,9},[5]={5}.
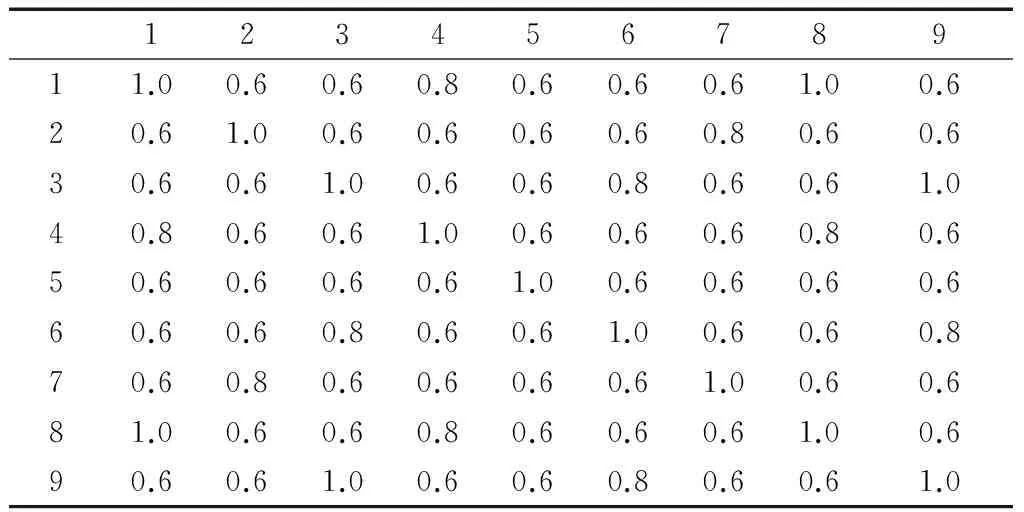
表3 模糊等价矩阵
2.2关系粒和粒化形式背景
本节将重点探讨关系粒和粒化背景,其中关系粒在粒化背景中扮演了重要角色.
定义4设K=(G,M,I)是一个形式背景,对于任意g∈G,m∈M,称[g]×m∈Gλ×M是一个关系粒;若Iλ⊆Gλ×M,则称Kλ=(Gλ,M,Iλ)是K的一个粒化形式背景.
由上述定义可知,任意关系粒[g]×m是否满足([g],m)∈Iλ,对于构造粒化背景至关重要,需要给出科学合理的判定准则.据此,本文提出了两类不同的判定方法,即一类是基于形式背景K的判定方法,另一类是基于概念格(B(K),≤)的判定方法.
定义5在形式背景(G,M,I)中,对于任意[g]×m∈Gλ×M,定义
其中ηλ是一个可信度函数.
显然,ηλ越大,([g],m)∈Iλ的可信度就越高;ηλ越小,([g],m)∉Iλ的可信度就越高.据此,引入参数0≤δ≤1,并将其作为判定([g],m)∈Iλ是否可信的阈值.依据实际需要,用户可以灵活调整阈值参数.
准则1对于粒[g]×m,若ηλ(g,m)≥δ,则([g],m)∈Iλ;若ηλ(g,m)≥/δ,则([g],m)∉Iλ.
例如,基于准则1,由表1可以导出如表4所示的粒化形式背景,其中λ=0.8且δ=0.6.
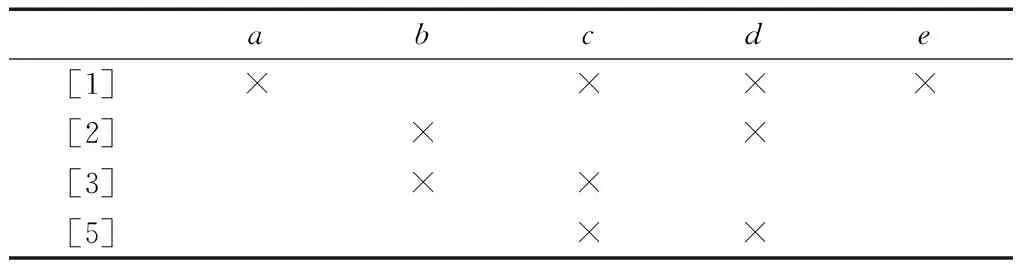
表4 基于准则1导出的表1的粒化背景
引理3设(G,M,I)是一个形式背景,对于任意g∈G和m∈M,(g,m)∈I当且仅当γg≤μm.
准则2_a设[g]×m是一个关系粒,对于∀g1∈[g],如果γg1≤μm,那么([g],m)∈Iλ;如果存在g1∈[g]满足γg1≤/μm,那么([g],m)∉Iλ.
上述准则等价于如下关系:
若ηλ(g,m)=1,则([g],m)∈Iλ;若ηλ(g,m)≠1,则([g],m)∉Iλ.
由上述讨论可知,准则2_a是准则1的一种特殊情况,但其判定条件较准则1太过苛刻,无助于用户从看似不相关的数据中发现有价值的信息.据此,可以借助下确界运算“∧”将准则2_a进一步弱化为准则2_b和2_c.
准则2_b设[g]×m是一个关系粒,若∧γ([g])≤μm,则([g],m)∈Iλ;若∧γ([g]) ≤/μm,则([g],m)∉Iλ.
准则2_c设[g]×m是一个关系粒,若∧γ([g])≤/μm,则([g],m)∉Iλ.当∧γ([g])≤μm时,若满足下述条件:
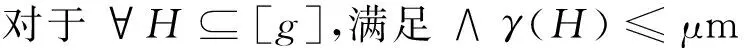
则([g],m)∈Iλ;若满足下述条件:
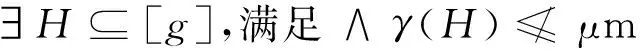
则([g],m)∉Iλ,其中|H|=2.
在上述基于概念格结构信息的判定准则中,由于∧γ([g])≤∧γ(H)≤γg≤μm,其中H⊆[g],显然,若作为判定条件,∧γ(H)≤μm要弱于γg≤μm,但强于∧γ([g])≤μm.即准则2_c判定条件的强弱介于准则2_b和准则2_a之间.尤其是当|[g]|较大时,准则2_b中的判定条件∧γ([g])≤μm将弱化,此时相应的判定结果有可能是不合理的.本质上,定理2和定理3可以从可信度函数的角度客观地反映准则2_c的合理性.
定理2在K=(G,M,I)中,设A⊆G,m∈M,有下述结论成立:
(1) 若∧γ(A)≤/μm,则(A×m)∩I=∅.
(2) 若存在g∈A,满足(g,m)∈I,则∧γ(A)≤μm.
证明:当∧γ(A)≤/μm时,假设存在g∈A满足(g,m)∈I,则由引理3即得γg≤μm,进而由∧γ(A)≤/γg可导出∧γ(A)≤μm,与条件∧γ(A)≤/μm相矛盾!故结论(1)成立.
当(g,m)∈I时,由引理3可知γg≤μm,进而由∧γ(A)≤γg即得结论(2)成立.证毕.
定理3在定理2中,有下述结论成立:
(1) 若∧γ(A)≤/μm,则ηλ(g,m)=0.
(2) 若ηλ(g,m)>0,则∧γ(A)≤μm.
(3) 设A、H⊆G,若H⊆A,则∧γ(A)≤∧γ(H).
证明:由定义5和定理2即得结论(1)和(2)成立.结论(3)由上、下确界的定义即得,在此不再详述.证毕.
在基于准则2_a、2_b或2_c的判定过程中,用户可以借助概念格(B(K),≤)的Hasse图,即概念格的结构信息,直观生动地判定任意关系粒[g]×m是否满足([g],m)∈Iλ.相对于准则2_a和准则2_b,用户选择准则2_c得到的判定结果可能会更合理一些,因为准则2_a的判定条件太强,不利于用户从看似不相关的数据中发现有价值的信息,而准则2_b的判定条件太弱,可能无法为构造粒化背景提供更加科学合理的依据.
以准则2_c为例,当λ=0.8且δ=0.6时,基于图2所示的格结构信息,用户可以从表1导出如表5所示的粒化背景.例如,在图3中,对于关系粒[1]×d,由于γ1∧γ8=γ1=γ8、γ1∧γ4=γ1、γ4∧γ8=γ8,且γ1∧γ4、γ1∧γ8、γ4∧γ8均小于μd,由此可以判定([1],d)∈Iλ;对于关系粒[3]×e,由于γ3∧γ9=γ3=γ9且γ3∧γ9≤/μe,所以判定([3],e)∉Iλ.
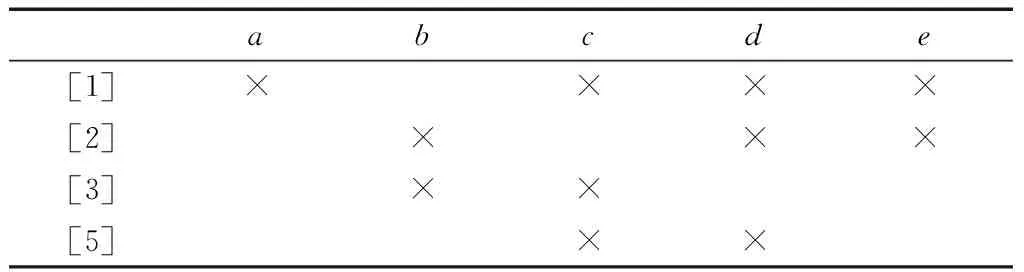
表5 基于准则2_c从表1导出的粒化背景
3 粒化概念和粒化概念格
在粒化背景Kλ=(Gλ,M,Iλ)中,对于任意对象粒集Aλ⊆Gλ和属性集B⊆M,定义1中的算子可以形式化描述为

称完备格(B(Kλ),≤)是(B(K),≤)的一个λ粒化概念格,其中B(Kλ)是Kλ中所有λ粒化概念组成的集合.例如,由表4可以导出一个如图3所示的概念格结构,该结构是图1所示概念格的一个粒化概念格.
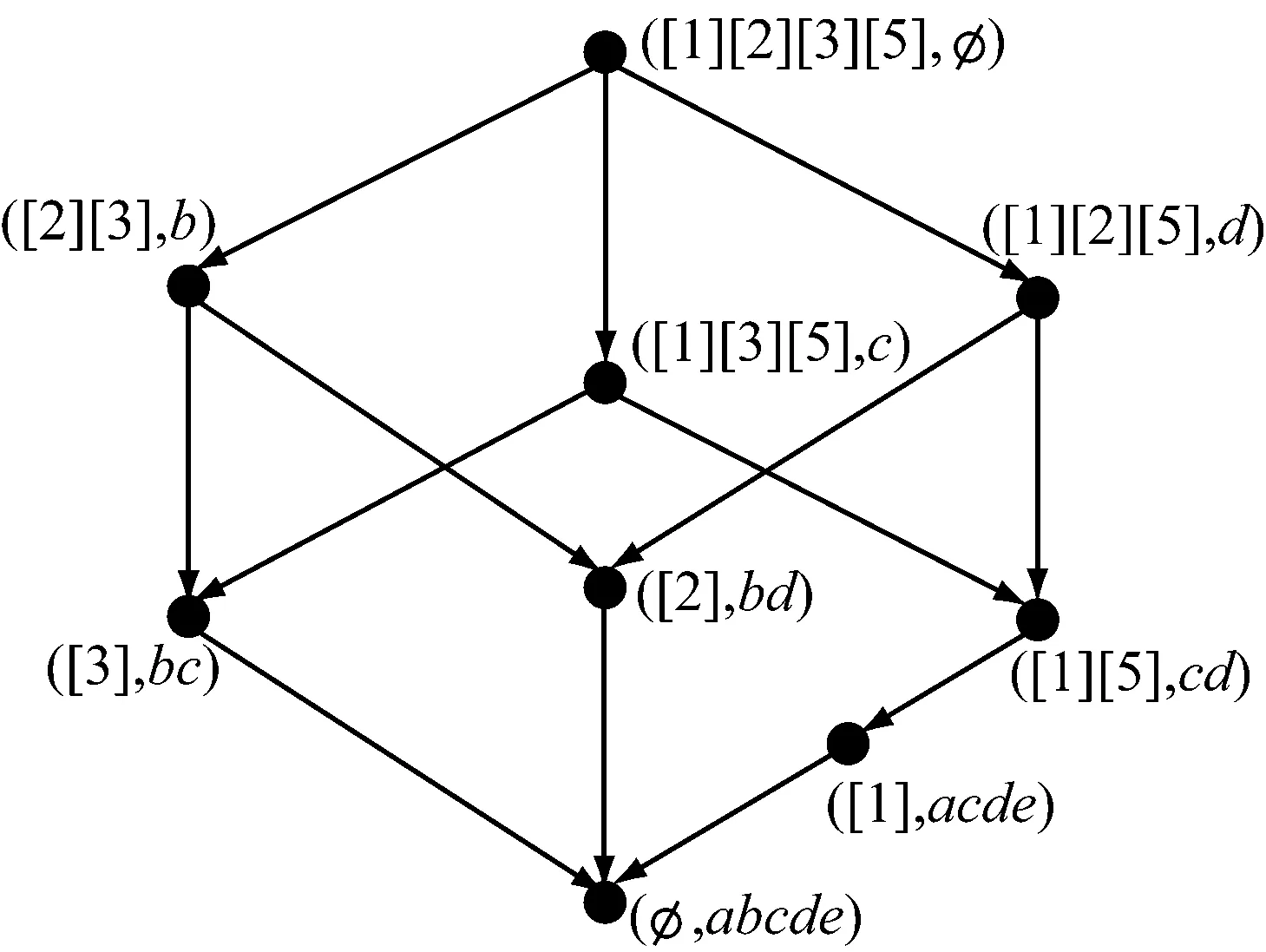
图3 由表4生成的粒化概念格
由上述讨论可知,粒化形式背景中的算子是基于对象粒定义的,虽然其与定义1中的算子形式上存在一定差异,但本质上它们属于同一类算子.
4 约简、核和蕴涵规则
约简、核、蕴涵规则等是概念格中常见的问题,本节将重点就上述问题给出一种基于粒化概念的求解方法.
定义6在K=(G,M,I)中,设B⊆M,如果m∈B且B′≠(B-m)′,则称m是B中的核属性,设D⊆B⊆M,若D是满足B′=D′的最小属性子集,则称D是B的一个约简;设B、D⊆M,称B→D是K中的蕴涵规则,简称规则.当B′⊆D′时,称B→D是一条确定规则;当B′D′时,称B→D是一条不确定规则.
定理4在Kλ=(Gλ,M,Iλ)中,对于任意B⊆M,记
若Int(Kλ)是一个由所有λ粒化概念内涵组成的集合,则B+=B″.
证明:由引理2即得.证毕.
定理5在Kλ=(Gλ,M,Iλ)中,设m∈B⊆M,若Eλ≠Fλ,则m是B中的核属性.其中,(Eλ,B+)∈B(Kλ)且(Fλ,(B-m)+)∈B(Kλ).
证明:由(Eλ,B+)∈B(Kλ)可知Eλ=(B+)′,进而由定理4可知Eλ=B‴=B′.同理可证Fλ=(B-m)′.由于Eλ≠Fλ,所以B′≠(B-m)′.显然,由定义6即得结论成立.证毕.
定理6在Kλ=(Gλ,M,Iλ)中,设D⊆B⊆M,若D是满足Eλ=Fλ的最小集合,则D是B的一个约简,其中(Eλ,B+)∈B(Kλ)且(Fλ,D+)∈B(Kλ).
证明:由(Eλ,B+)∈B(Kλ)可知Eλ=(B+)′,进而由定理4可知Eλ=B‴=B′.同理可证Fλ=D′.由于Eλ=Fλ,所以B′=D′,又由于D是满足B′=D′的最小集合,故由定义6即得结论成立.证毕.
概念格非常适合发现一些有价值的规则型知识,置信度和支持度是对规则的重要补充和定量描述.通常,在形式背景K=(G,M,I)中,就某条规则B→D而言,其置信度是指在B出现的条件下,D出现的概率,通常被形式化描述为
如果Conf(B→D)=1,则说明当B出现时,D一定会出现.如果置信度太低,则说明B和D之间的关系较弱,B→D在实际应用中的价值不高.支持度本质上揭示了B与D同时出现的概率,通常被形式化描述为
如果支持度较高,则说明B与D在一定程度上是相关的.事实上,在实际应用中,用户往往会对置信度和支持度提出一定的要求,进而获取置信度和支持度较高的规则.
基于上述讨论,关于规则的置信度和支持度,本文给出了基于对象粒Gλ的定义.
定义7在Kλ=(G,M,Iλ)中,对于任意规则B→D,其置信度和支持度分别定义为
其中,(Eλ,B+)∈B(Kλ)且(Fλ,D+)∈B(Kλ).
例如,在表4中,对于规则c→de,由于([1][3][5],c)和([1],de)是λ粒化概念,又{c}+={c}且{d,e}+={a,c,d,e},故有
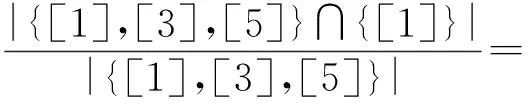
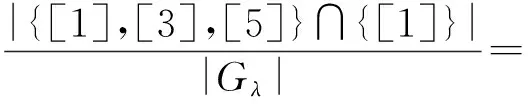
通常,形式背景中存在着大量的冗余规则,往往导致一些有价值的规则被淹没在海量的规则中.一些常见的确定的冗余规则有:若B⊆B1且D1⊆D,则B1→D1相对于确定规则B→D是冗余的,此时称B1→D1是一条相对冗余规则;若D⊆B,称B→D是一条绝对冗余规则.
基于上述讨论,在一个粒化形式背景中,可以删除一些绝对冗余规则和相对冗余规则,并最终得到一个规模较小的确定规则集,称为源规则集.例如,表1和4中源规则集如表6所示.

表6 源规则集
5 结论及展望
把粒计算融入概念格研究中,通过降低知识获取的“分辨率”,扩大知识度量的“尺度”,有助于人们从不相关的数据中发现一些潜在的有价值信息,而且也能有效简化复杂的格结构和压缩概念的规模.在粒化过程中,提出了一种新的基于概念基的求解思路.所谓概念基是指一个由低层概念构成的集合,其在信息粒化的整个过程中扮演了重要的角色.特别地,在信息粒化过程中,还提出了一种基于下确界运算的求解思路,它与传统模型最大的区别是融合了概念格的结构信息.
总之,本文把粒计算引入到概念格研究中,对于概念格的拓展不失为一种有效的手段,理论和实例证明了本文提出的结论的合理性和有效性.虽然概念格是数据分析的有效工具,但面对规模庞大的数据集以及复杂的知识发现任务,在实际应用中仍存在着许许多多的问题.本文的研究工作仅仅是一个尝试,关于粒计算与概念格的融合理论还有待进一步深入.
参考文献:
[1]Wille R. Restructuring lattice theory: an approach based on hierarchies of concepts [C]∥Ordered Sets. Dordrecht: Reidel, 1982: 445-470.
[2]Ganter B, Wille R. Formal concept analysis: mathematical foundations [M]. Berlin: Springer-Verlag, 1999.
[3]Li J H, Mei C L, Lü Y J. Incomplete decision contexts: approximate concept construction, rule acquisition and knowledge reduction [J]. International Journal of Approximate Reasoning, 2013, 54(1): 149.
[4]薛金蓉, 安秋生, 郑军. 概念格的内涵缩减与数据库推理依赖[J]. 计算机研究与发展, 2014, 51(1): 96.
XUE Jinrong, AN Qiusheng, ZHENG Jun. Intent reduction of concept lattice and database inference dependence [J]. Journal of Computer Research and Development, 2014, 51(1): 96.
[5]杨丽, 徐扬. 基于逻辑合取的语言真值概念格合并算法[J]. 电子学报, 2013, 41(11): 2149.
YANG Li, XU Yang. Union algorithm of linguistic truth-valued concept lattice based on logical conjunction [J]. ACTA Electronica Sinica, 2013, 41(11): 2149.
[6]智慧来, 智东杰, 刘宗田. 概念格合并原理与算法[J]. 电子学报, 2010, 38(2): 455.
ZHI Huilai, ZHI Dongjie, LIU Zongtian. Theory and algorithm of concept lattice union [J]. ACTA Electronica Sinica, 2010, 38(2): 455.
[7]张磊, 张宏莉, 殷丽华, 等. 概念格的属性渐减原理与算法研究[J]. 计算机研究与发展, 2013, 50(2): 248.
ZHANG Lei, ZHANG Hongli, YIN Lihua,etal. Theory and algorithms of attribute decrement for concept lattice [J]. Journal of Computer Research and Development, 2013, 50(2): 248.
[8]谢志鹏, 刘宗田. 概念格的快速渐进式构造算法[J]. 计算机学报, 2002, 25(5): 490.
XIE Zhipeng, LIU Zongtian. A fast incremental algorithm for building concept lattice [J]. Chinese Journal of Computers, 2002, 25(5): 490.
[9]刘宗田, 强宇, 周文, 等. 一种模糊概念格模型及其渐进式构造算法[J]. 计算机学报, 2007, 30(2): 184.
LIU Zongtian, QIANG Yu, ZHOU Wen,etal. A fuzzy concept lattice model and its incremental construction algorithm [J]. Chinese Journal of Computers, 2007, 30(2): 184.
[10]Zhai Y H, Li D Y, Qu K S. Fuzzy decision implications [J]. Knowledge-Based Systems, 2013, 37: 230.
[11]Zhai Y H, Li D Y, Qu K S. Decision implication canonical basis: a logical perspective [J]. Journal of Computer and System Sciences, 2015, 81: 208.
[12]胡可云,陆玉昌,石纯一. 基于概念格的分类和关联规则的集成挖掘方法[J]. 软件学报, 2000, 11(11): 1478.
HU Keyun, LU Yuchang, SHI Chunyi. An integrated mining approach for classification and association rule based on concept lattice [J]. Journal of Software, 2000, 11(11): 1478.
[13]梁吉业, 王俊红. 基于概念格的规则产生集挖掘算法[J]. 计算机研究与发展, 2004, 41(8): 1339.
LIANG Jiye, WANG Junhong. An algorithm for extracting rule-generating sets based on concept lattice [J]. Journal of Computer Research and Development, 2004, 41(8): 1339.
[14]马垣, 张学东, 迟呈英. 紧致依赖与内涵亏值[J]. 软件学报, 2011, 22(5): 962.
MA Yuan, ZHANG Xuedong, CHI Chengying. Compact dependencies and intent waned values [J]. Journal of Software, 2011, 22(5): 962.
[15]Mi J S, Leung Y, Wu W Z. Approaches to attribute reduction in concept lattices induced by axialities [J]. Knowledge-Based Systems, 2010, 23(6): 504.
[16]张文修, 魏玲, 祁建军. 概念格的属性约简理论与方法[J]. 中国科学: E辑, 2005, 35(6): 628.
ZHANG Wenxiu, WEI Ling, QI Jianjun. Attribute reduction theory and approach to concept lattice [J]. Science in China: Series E, 2005, 35(6): 628.
[17]李冲, 曹吉鸣, 马腾. 基于形式概念分析的项目成员综合相似度计算[J]. 同济大学学报:自然科学版, 2014, 42(6): 983.
LI Chong, CAO Jiming, MA Teng. Integrated similarity calculation of project members based on formal concept analysis [J]. Journal of Tongji University: Natural Science, 2014, 42(6): 983.
[18]李立峰, 张东晓. 概念格在二值命题逻辑命题集约简中的应用[J]. 电子学报, 2007, 35(8): 1538.
LI Lifeng, ZHANG Dongxiao. The application of concept lattice theory in the reduction of the proposition set in two-valued propositional logic [J]. ACTA Electronica Sinica, 2007, 35(8): 1538.
[19]Shao M W, Liu M, Zhang W X. Set approximations in fuzzy formal concept analysis [J]. Fuzzy Sets and Systems, 2007, 158(23): 2627.
[20]Kang X P, Li D Y, Wang S G,etal. Formal concept analysis based on fuzzy granularity base for different granulations [J]. Fuzzy Sets and Systems, 2012, 203: 33.
[21]Burusco A, Fuentes-Gonzales R. Construction of the L-fuzzy concept lattice [J]. Fuzzy Sets and Systems, 1998, 97:109.
[22]Wei L, Qi J J. Relation between concept lattice reduct and rough set reduct [J]. Knowledge-Based Systems, 2010, 23(8): 934.
[23]Kang X P, Li D Y, Wang S G,etal. Rough set model based on formal concept analysis [J]. Information Sciences, 2013, 222: 611.
[24]Chen J K, Li J J, Lin Y J,etal. Relations of reduction between covering generalized rough sets and concept lattices [J]. Information Sciences, 2015, 304: 16.
[25]仇国芳, 张志霞, 张炜. 基于粗糙集方法的概念格理论研究综述[J]. 模糊系统与数学, 2014, 28(1): 168.
QIU Guofang, ZHANG Zhixia, ZHANG Wei. A survey for study on concept lattice theory via rough set [J]. Fuzzy Systems and Mathematics, 2014, 28(1): 168.
[26]Lai H L,Zhang D X.Concept lattices of fuzzy contexts: formal concept analysis vs.rough set theory [J].International Journal of Approximate Reasoning, 2009, 50: 695.
[27]Wang L D, Liu X D. Concept analysis via rough set and AFS algebra [J]. Information Sciences, 2008, 178:4125.
[28]Yao Y Y. Concept lattices in rough set theory [C] // Proceedings of the 2004 IEEE Annual Meeting of the North American Fuzzy Information Processing Society (NAFIPS04). Piscataway: IEEE, 2004: 796.
[29]Dias S M, Nogueira B M, Zarate L E. Adaptation of FCANN method to extract and represent comprehensible knowledge from neural networks [J]. Studies in Computational Intelligence, 2008, 134:163.
[30]Jiang L, Deogun J. SPICE: a new frame work for data mining based on probability logic and formal concept analysis [J]. Fundamenta Informaticae, 2007, 78: 467.
[31]仇国芳, 马建敏, 杨宏志, 等. 概念粒计算系统的数学模型[J]. 中国科学: E辑, 2009, 39 (12): 1239.
QIU Guofang, MA Jianmin, YANG Hongzhi,etal. Mathematical model of concept granule computing system [J]. Science in China: Series E, 2009, 39(12): 1239.
[32]Kang X P, Li D Y, Wang S G. Research on domain ontology in different granulations based on concept lattice [J]. Knowledge-Based Systems, 2012, 27: 152.
[33]Wu W Z, Leung Y, Mi J S. Granular computing and knowledge reduction in formal contexts [J]. IEEE Transactions on Knowledge and Data Engineering, 2009, 21(10): 1461.
[34]Sarmah A K, Hazarika S M, Sinha S K. Formal concept analysis: current trends and directions [J]. Artificial Intelligence Review, 2015, 44(1): 47.
[35]Lee H S. An optimal algorithm for computing the max-min transitive closure of a fuzzy similarity matrix [J]. Fuzzy Sets and Systems, 2001, 123: 129.
收稿日期:2015-08-11
基金项目:国家自然科学基金(61273304,61202170);中国博士后科学基金(2014M560352);教育部高等学校博士学科点专项科研基金(20130072130004)
通讯作者:苗夺谦(1964─),男,教授、博士生导师,工学博士,主要研究方向为智能信息处理、人工智能与模式识别、数据挖掘、粗糙集、粒计算等.E-mail:miaoduoqian@163.com
中图分类号:TP182
文献标志码:A
Expanded Concept Lattice Based on Granular Computing
KANG Xiangping1,2, MIAO Duoqian1,2
(1. College of Electronics and Information Engineering, Tongji University, Shanghai 201804, China; 2. Key Laboratory of Embedded System and Service Computing of the Ministry of Education, Tongji University, Shanghai 201804, China)
Abstract:By introducing granular computing into concept lattice, and integrating similarity measure model and structure information of concept lattice, the paper proposes an expanded concept lattice model based on granular computing. It can help to expand intent and extent of classical concept, and also can effectively reduce the scale of concepts to some extent. The model is not only a useful attempt and exploration for the fusion of these two theories, but also an effective means of expanding the classical concept lattice.
Key words:concept lattice; granular computing; relation granules; granulation concept lattice
第一作者: 康向平(1982─),男,工学博士,主要研究方向为概念格、粗糙集、粒计算等.E-mail:tongji_kangxp@sina.com
