发动机缸体加工方案选择与操作排序协同优化
2016-08-13李爱平陆嘉庆刘雪梅
李爱平, 朱 璟, 陆嘉庆, 刘雪梅
(同济大学 机械与能源工程学院,上海 201804)
发动机缸体加工方案选择与操作排序协同优化
李爱平, 朱璟, 陆嘉庆, 刘雪梅
(同济大学 机械与能源工程学院,上海 201804)
摘要:提出一种基于蚁群算法的发动机缸体加工方案选择与操作排序协同优化方法.考虑到部分零件特征有多个可行加工方案,在每次总迭代中为此类特征随机选择一种加工方案,并根据特征约束矩阵和操作优先级系数自动生成对应的操作约束矩阵.通过子迭代中的遗传算法进行操作排序优化,以装夹、刀具和机床3类制造资源的综合变换次数最少为目标得出子最优解,并在总迭代中利用精英保留策略获得全局最优工艺路线.最后,通过复杂的发动机缸体实例验证了该方法的有效性.
关键词:发动机缸体; 加工方案选择; 操作排序; 蚁群算法
计算机辅助工艺规划(CAPP)系统中最重要的2个功能是加工方案选择和操作排序优化,即为零件的每个特征选择加工方案(加工链)和对所有加工操作进行最优化排序,两者相互关联又相互制约.针对这2个问题,国内外学者进行了多方面的研究.文献[1-3]分别采用神经网络、模糊综合评价与灰色关联分析相结合、层次分析法与粒子群算法相结合的方法对加工方案选择问题进行研究.文献[4-6]采用遗传算法研究了操作排序问题.文献[7-9]针对操作排序问题运用蚁群算法进行求解.此外还有采用混合蝙蝠算法[10]、混合粒子群算法[11]等对工艺规划问题进行研究.但是,上述文献大多单独针对加工方案选择或操作排序进行研究,其工艺规划方式与传统的工艺规划类似——即工艺专家先为每个特征选择一个加工方案,然后将所有特征加工方案的操作组合在一起进行最优化排序.这种串行处理方法最大的缺点是最优解可能在选择加工方案时丢失.为克服串行处理方法的这一缺点,就需要协同考虑加工方案选择和操作排序.
文献[12-14]同时考虑了加工方案选择和操作排序问题,基于遗传算法获得了全局最优结果.但文献[12]中加工方案选择过程较繁琐,且单个特征可选加工方案过多,会导致算法运用于复杂零件计算时效率过低.文献[13]通过多个实例验证了其算法的有效性,但在复杂零件上的运用还有待验证.文献[14]先选择最优的加工链然后排序,其本质上还是串行的处理方式.另外,相比文献[12-14]所用的遗传算法,蚁群算法作为一种具有全局寻优、信息正反馈、启发式搜索和分步式计算特征的概率型技术,在求解旅行商问题(TSP)、分配问题和job-shop调度等组合优化问题上表现出了良好的性能[8].本文在前人研究的基础上,进一步协同考虑加工方案选择和操作排序问题,利用蚁群算法简化寻优过程,并运用于复杂零件的工艺规划.
发动机缸体作为典型的复杂箱体类零件,工艺设计复杂,经验性很强,其工艺特点主要为:结构形状复杂,加工的平面、孔多,壁厚不均、刚度低,加工精度要求高.随着社会对产品多样化、低制造成本及短制造周期等需求日趋迫切,柔性制造系统发展颇为迅速.发动机缸体生产也由以前的单品种、大批量刚性生产线逐步向多品种、中小批量柔性生产线发展.就发动机缸体的柔性生产线而言,其主要优点有:设备利用率高、在制品少、生产能力相对稳定、产品质量高、运行灵活以及产品应变能力大.因此对于给定的发动机缸体,快速高效的生成其加工工艺对于一个企业来说就显得尤为重要.
本文以发动机缸体为研究对象,针对发动机缸体柔性生产线工艺规划中加工方案选择和操作排序这2个重要环节,提出一种基于蚁群算法的协同优化方法.综合考虑装夹方式、刀具和机床的变换,以制造资源综合变换次数最少为目标,最终获得全局最优工艺路线.本文算法在处理发动机缸体这类复杂零件上具有优化效果好、计算效率高的特点.
1 数学模型
1.1特征元和加工方案
零件特征是包括零件一定的几何形状、工程意义和加工要求的一组信息的集合,是构成零件几何形状和信息模型的基本单元.零件通常由许多基本的加工特征构成,如面、孔、槽等,这些基本的加工特征被称为特征元.
设某零件一共有N个特征元,则所有特征元组成的集合可表示为
式中:fi表示零件的第i个特征元,i=1,2,…,N.
由于每个特征元可能对应着多种加工方案,因此特征元fi又可以表示为
式中:B为特征元编号,对于某个具体零件,零件中所有特征元都有唯一的编号;E为特征名称,根据功能不同,相应的特征具有相应的名称,此外,还包括特征的基本属性如螺纹孔、直径等;T为特征元的加工方案集,不同特征元可能对应不同数量的加工方案.进一步,fi的加工方案集Ti又可以表示为
式中:Tin为fi的第n种加工方案.由于加工方案一般由多个操作组成,所以Tin又可以表示为

1.2操作信息表达
对零件的每个特征元选择一种加工方案,每一种加工方案又包含几个操作,所有这些操作经过排序就组成了一条完整的工艺路线.设一条工艺路线中包含的操作总数为L,则工艺路线可表示为
式中:oj表示工艺路线中第j个操作.由于每个操作对应有多种属性,所以oj又可以表示为

2 约束条件及目标函数
2.1约束条件的建立
2.1.1强制性约束
强制性约束是为了避免加工操作间发生干涉及保证加工质量提出的一系列必须遵守的工艺优先约束,也称加工顺序约束,其制定规则如下所示:
(1) 先面后孔.待加工面特征下存在孔系特征时,该面的粗(精)加工操作须先于其孔系粗(精)加工操作.
(2) 先粗后精.同个特征的若干操作,须按照其工艺既定先后次序完成.
(3) 基准优先.必须先加工作为定位基准的面和孔,再加工其他表面特征.
(4) 先主后次.槽、倒角等辅助特征的加工一般在主特征的加工完成之后进行.
(5) 其他由用户自定义的加工顺序约束.
本文引入特征约束矩阵Y和操作优先级系数P来保证操作排序中的加工顺序约束.
对于某零件的特征元集F={f1,f2,…,fN},特征元在工艺路线中优先关系可以使用一个N×N的特征约束矩阵YN×N=(yij)表示,i,j=1,2,…,N.
(1)
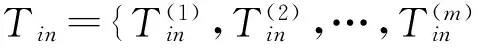
特征约束矩阵和操作优先级系数的共同作用,能够严格保证工艺路线满足加工顺序约束,进而保证零件的加工要求.
对于一个确定零件,其特征约束矩阵以及各特征元不同加工方案中操作的优先级系数都是确定的.当每个特征元都选定了加工方案后,根据特征约束矩阵和操作优先级系数便可以得到对应的操作约束矩阵RL×L=(ruv),u,v=1,2,…,L,
(2)

根据如上定义,对于特征约束矩阵中的任一操作w,可以得出:当|Vw|=0的时候,操作w可以作为工艺路线的起点.
2.1.2最优性约束
最优性约束的目的是使零件的工艺路线更加合理.工艺路线的设计不仅需要考虑零件的几何形状、技术要求、工艺方法等因素,还要综合考虑生产率、加工成本、加工精度等约束.由于多个因素之间相互制约,难以在一次工艺路线中同时满足所有因素,因此本文从制造资源(机床、刀具和夹具)入手,对工艺路线的最优性约束展开分析.
在实际加工过程中,为了缩短制造周期,提高生产率,应尽量降低制造资源的更换频率.装夹变换次数减少可以降低装夹误差,从而提高加工精度,并增加工艺过程的稳定性.而加工精度和工艺过程稳定性的提高将使产品的废品率降低,从而使加工成本降低.减少换刀次数,可以减少非切削加工时间,提高机床的利用率.综上,通过约束制造资源的变换次数,可以有效满足工艺路线规划中对高生产率、低加工成本和高制造精度的共同追求.因此本文的最优性约束可表示为:①尽量减少机床变换次数;②尽量减少刀具变换次数;③尽量减少装夹变换次数.
2.2目标函数的建立
根据最优性约束分析,确定工艺路线优化的目标为:制造资源的综合变换次数最少.定义相邻两操作oj和oj+1之间的制造资源变换率为
(3)
式中:λJ、λC和λM分别表示装夹方式变换、刀具变换和机床变换的权重系数,一般由工艺专家根据具体情况确定;δ(Jj,Jj+1)、δ(Cj,Cj+1)和δ(Mj,Mj+1)分别表示装夹方式、刀具和机床的变换;δ(a,b)是一个判断函数,表示为

由式(3)可进一步定义某工艺路线Ox的制造资源综合变换次数为
(4)
则目标函数可表示为minZ(x).
3 基于蚁群算法的加工方案选择与操作排序协同优化方法
针对发动机缸体零件工艺路线决策问题,本文在对零件特征、操作进行知识表示和对基本蚁群算法进行改进的基础上,提出一种加工方案选择与操作排序协同优化方法.
3.1禁忌准则
蚂蚁在进行操作选择时,符合禁忌准则的操作会被放入禁忌列表tabuk中,在遍历过程中将会被筛除.禁忌操作分两类:①已经完成的操作;②不满足强制性约束的操作.在本文的实际运算过程中,仅将已完成的操作放入禁忌列表,且每选择一个操作便解除该操作对剩余操作的约束.这样仅需寻找剩余操作中不受任何约束的操作即为下一步可行操作,相比传统的禁忌列表处理方式效率更高.
3.2路径转移概率
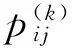
(5)
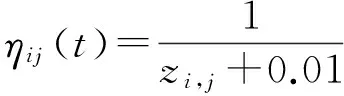
3.3信息素更新
当蚂蚁k完成对所有操作节点的遍历后,各路径上残留信息素按下式进行更新调整:
(6)
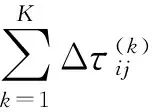
(7)
式中:Q是一个正常数;lk表示第k只蚂蚁在本次迭代中所走过的路径总长度.
3.4算法流程
基于上述蚁群算法的运用,结合可变的操作约束矩阵,并引入加工方案选择和操作排序双重迭代模式,得到加工方案选择与操作排序协同优化方法,其算法流程如图1所示.
为更清楚地表明此方法,进一步将算法流程描述如下:
步骤1设置总迭代计数器S=1,最大总迭代次数为Smax.
步骤2为每个特征元fi随机选择一种加工方案Tin,根据特征约束矩阵Y和各Tin的操作优先级系数P生成相应的操作约束矩阵RL×L.


图1 算法流程图
步骤4令k=1.


步骤7j=j+1;若j 步骤8k=k+1;若k≤K,则转步骤5. 步骤9根据式(4)计算各蚂蚁的目标函数值Z,若蚂蚁x的目标函数值Zx小于当前的最优值,则更新当前的最优工艺路线为Ox;按式(6)更新各路径上的信息素τij. 步骤11若本次子迭代的最优值小于当前的子迭代最优值,则更新当前的最优工艺路线. 步骤12S=S+1;若S≤Smax,则转步骤2;否则,输出全局最优工艺路线,结束算法. 此处将以某柴油发动机企业某缸体为例,对其 加工方案选择及操作排序进行协同优化,以验证本文算法的有效性. 4.1实例描述 该产品零件及其特征如图2所示.此零件需在全部6个面上进行加工,其工艺包括铣削、镗削、钻孔、扩孔、铰孔、攻螺纹等.在对其相同面上相同特征进行聚类后,仍拥有50个特征元.通过前期规划得到各个特征元可选择加工方案、对应刀具、可选择机床以及可选择装夹方式等信息.由于篇幅原因,此处仅列举其中6个典型特征元信息,见表1. a10、20和40面特征b30、50和60面特征 图2发动机缸体零件及其特征 Fig.2Engine cylinder and its features 表1 特征元信息统计表 如表1所示,每个特征元对应1种或多种加工方案,如特征元205,既可通过钻-扩-铰方案加工,也可以通过钻-粗镗-半精镗方案加工;在本例中,共有9个特征元对应2种加工方案,其余41个特征元均只有1种加工方案.由于零件10、20、50和60面的精度要求比较高,其精铣操作需在精加工机床上进行,因此为了避免该要求与强制性约束中先面后孔条件的冲突,特将这几个特征元拆分成2个特征元,例如:将特征元10面拆分成10-1和10-2,分别代表10面粗加工和10面精加工.在机床的选择上,由于本缸体均采用加工中心进行加工,因此将机床分为2种:粗加工机床(1)和精加工机床(2). 本零件加工共涉及47种刀具,具体刀具信息如表2所示. 零件的装夹方式根据企业实际情况分为5种,各个特征的各步操作,分别对应1种或多种装夹方式,5种装夹方式及其主要加工内容如表3所示. 4.2参数设置 目标函数的权重系数λJ、λC和λM反映了装夹方式变换、刀具变换和机床变换3个优化目标之间的相对重要关系,综合考虑实际加工中三者所花费时间及三者对于制造精度的影响,并通过企业推荐以及算法的验证,本案例取λJ=0.3、λC=0.15、λM=0.55. 表2 零件所用刀具信息表 表3 装夹方式及其主要加工内容 4.3计算结果 采用以上参数,通过基于蚁群算法的加工方案选择与操作排序协同优化方法,为零件选择一条最优工艺路线,使用Matlab2010软件进行计算,得到目标函数值Z(x)随总迭代次数S的收敛图如图3所示. 所得的全局最优解Zmin=0.55×1+0.3×4+0.15×59=10.6,其中机床变换1次,装夹方式变换4次,刀具变换59次.对应的最优工艺路线如表4所示,表中括号内的数字为操作所对应的刀具编号. 实例中对应2种加工方案的9个特征元,最终选择的加工方案结果如表5所示.从表中可以看出,直径相同的不同特征元选择的加工方案是一致的.这样的选择可以有效减少刀具的数量,从而减少换刀次数和刀具成本,此结果也印证了本文算法的有效性. 机床装夹操作11粗铣30、40面(1),精铣40、30面(1),钻302、401(23),攻401、302(11),锪水闷孔301(9),铰水闷孔301(18)12粗铣、半精铣10面(1),粗铣、半精铣60面(1),钻604(38),钻602(23),钻603(32),攻602(11),钻605(37),攻603(14),钻601(35),精铣60面(2),扩601(36),铰601(16)13粗铣、半精铣50面(1),粗铣、半精铣20面(1),钻506、208(23),钻204(32),攻506、208(11),钻505(24),钻206(37),钻502(35),锪501、201(9),钻210、209(19),钻503(27),钻205(38),扩505(25),钻504(28),攻209(10),攻503(12),铰505(26),铰501、201(18),扩205(39),粗镗207、507(6),扩504(29),钻202(34),铰205(17),钻203、307、304(33),扩502、202、203(36),铰203、202、502、304(16),钻211(20),铰定位孔504(15)14钻107(30),钻303、106、402(27),钻105(24),钻305(37),钻308(22),钻104(21),钻102(31),钻306(32),攻303、402(12),粗镗缸孔101(3),攻102(13),钻103(20)25半精镗缸孔101(4),精铣10、50、20面(2),精镗缸孔101(5),半精镗507、207(7),精镗507、207(8) 在企业现有的工艺方案中,该缸体制造资源变换次数为:机床变换1次,装夹方式变换4次,刀具变换78次.据此可计算出企业该缸体现有工艺路线的制造资源综合变换次数Z=0.55×1+0.3×4+0.15×78=13.45.本文算法所得工艺路线与其相比,制造资源综合变换次数降低了21.19%,有效减少了缸体加工过程中制造资源的变换次数,尤其是刀具的变换次数,进而提高了机床利用率,提升了加工过程的稳定性. 表5 加工方案选择结果 由此可见,本文方法能够有效地对发动机缸体零件进行加工方案选择及操作排序协同优化,选出全局最优工艺路线,且本方法的收敛速度快,实例计算所需时间较短,能够快速得出最优解.需要说明的是,按本文所述方法生成的工艺路线仅包含了关键工序,其余辅助工序、热处理工序等需要根据具体加工条件和要求另行添加. 本文针对发动机缸体零件柔性生产线前期工艺规划中的工艺路线制定问题,提出一种基于蚁群算法的加工方案选择与操作排序协同优化方法.在一部分零件特征加工方案不定的情况下,先对各特征的加工方案进行随机选择,再对所选加工方案进行操作排序,多次循环迭代后得到全局最优工艺路线.在约束条件处理上,采用了变化的操作约束矩阵处理方式,有效提高了计算效率.在目标函数的选择上,综合考虑了装夹方式、刀具和机床的变换,使所得工艺路线更具合理性.最后,对某企业某柴油发动机缸体零件进行实例验证,取得了满意的结果,说明了该方法的有效性和高效性.然而,本文只是考虑了加工方案选择和操作排序的优化问题,工艺路线优化问题种类较多,其余问题还应在以后研究中加以关注. 参考文献: [1]Deb S, Ghosh K, Paul S. A neural network based methodology for machining operations selection in computer-aided process planning for rotationally symmetrical parts[J]. Journal of Intelligent Manufacturing, 2006, 17(5): 557. [2]王佩, 张定华, 陈冰, 等. 基于模糊综合评价与灰色关联分析法的多工艺方案评价[J]. 航空动力学报, 2012, 27(9): 2075. WANG Pei, ZHANG Dinghua, CHEN Bing,etal. Evaluation of multi-process plans based on fuzzy comprehensive evaluation and grey relational analysis[J]. Journal of Aerospace Power, 2012, 27(9): 2075. [3]Hu Y J, Wang Y, Wang Z L,etal. Machining scheme selection based on a new discrete particle swarm optimization and analytic hierarchy process[J]. Artificial Intelligence for Engineering Design, Analysis and Manufacturing, 2014, 28(1): 71. [4]郝建波, 李宗斌, 赵丽萍. 工步排序问题的约束模型及其遗传算法的求解[J]. 西安交通大学学报, 2008, 42(7): 860. HAO Jianbo, LI Zongbin, ZHAO Liping. Genetic algorithm with constraint model for sequencing workingsteps on machining center [J]. Journal of Xi’an Jiaotong University, 2008, 42(7): 860. [5]Bo Z W, Hua L Z, Yu Z G. Optimization of process route by genetic algorithms[J]. Robotics and Computer-Integrated Manufacturing, 2006, 22(2): 180. [6]Huang W, Hu Y, Cai L. An effective hybrid graph and genetic algorithm approach to process planning optimization for prismatic parts[J]. The International Journal of Advanced Manufacturing Technology, 2012, 62(9/12): 1219. [7]Liu X, Yi H, Ni Z. Application of ant colony optimization algorithm in process planning optimization[J]. Journal of Intelligent Manufacturing, 2013, 24(1): 1. [8]常智勇, 杨建新, 赵杰, 等. 基于自适应蚁群算法的工艺路线优化[J]. 机械工程学报, 2012, 48(9): 163. CHANG Zhiyong, YANG Jianxin, ZHAO Jie,etal. Optimization of process based on adaptive ant colony algorithm[J]. Journal of Mechanical Engineering, 2012, 48(9): 163. [9]刘伟, 王太勇, 周明, 等. 基于蚁群算法的工艺路线生成及优化[J]. 计算机集成制造系统, 2010, 16(7): 1378. LIU Wei, WANG Taiyong, ZHOU Ming,etal. Generation and optimization of process routing based on ant colony algorithm[J]. Computer Integrated Manufacturing Systems, 2010, 16(7): 1378. [10]Wang J, Fan X, Zhao A,etal. A hybrid bat algorithm for process planning problem[J]. Internation Federation of Automatic Control, 2015, 48(3): 1708. [11]Wang Y F, Zhang Y F, Fuh J Y H. A hybrid particle swarm based method for process planning optimisation[J]. International Journal of Production Research, 2012, 50(1): 277. [12]Hua G, Zhou X, Ruan X. GA-based synthesis approach for machining scheme selection and operation sequencing optimization for prismatic parts[J]. The International Journal of Advanced Manufacturing Technology, 2007, 33(5/6): 594. [13]郑永前, 王阳. 基于遗传算法的加工工艺决策与排序优化[J]. 中国机械工程, 2012, 23(1): 59. ZHENG Yongqian, WANG Yang. Optimization of process selection and sequencing based on genetic algorithm[J]. China Mechanical Engineering, 2012, 23(1): 59. [14]黄华, 李爱平, 徐立云. 面向加工中心的工艺方案优化技术[J]. 同济大学学报: 自然科学版, 2010, 38(1): 118. HUANG Hua, LI Aiping, XU Liyun. CNC-based optimized machining scheme[J]. Journal of Tongji University: Natural Science, 2010, 38(1): 118. 收稿日期:2015-09-28 基金项目:国家高档数控机床与基础制造装备科技重大专项(2011ZX04015-022) 中图分类号:TH162 文献标志码:A Cooperative Optimization of Machining Scheme Selection and Operation Sequencing for Engine Cylinder LI Aiping, ZHU Jing, LU Jiaqing, LIU Xuemei (School of Mechanical Engineering, Tongji University, Shanghai 201804, China) Abstract:An ant colony algorithm based cooperative optimization for machining scheme selection and operation sequencing of engine cylinder is proposed. Considering that features have alternative machining schemes, one machining scheme is chosen randomly for every feature in total iterations, and an operating-constraint matrix is created automatically based on feature-constraint matrix and operation priority. Aiming at minimizing the transforming times of manufacturing resources that contain setups, tools and machine tools, a son optimal solution is found by the ant colony algorithm in the son iteration. In addition, a global optimal process line is ensured to be gotten through the usage of elitist preserving strategy in the total iteration. Finally, an engine cylinder case is illustrated to prove the validity of the proposed method. Key words:engine cylinder; machining scheme selection; operation sequencing; ant colony algorithm 第一作者: 李爱平(1951—),女,教授,博士生导师,工学博士,主要研究方向为制造系统与自动化.E-mail:limuzi@tongji.edu.cn
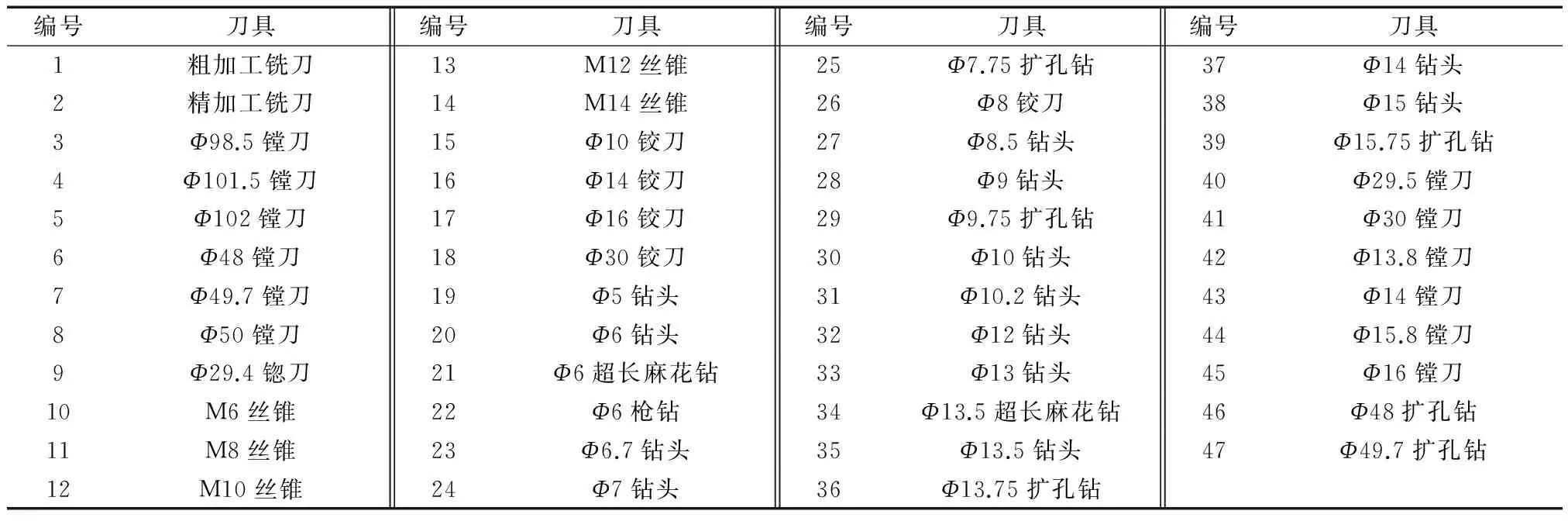
4 实例验证






5 结语
