全断面隧道掘进机破岩机理离散元分析

蒋明镜， 孙　亚， 王华宁， 袁聚云

(1. 同济大学 土木工程防灾国家重点实验室， 上海 200092； 2. 同济大学 岩土及地下工程教育部重点实验室， 上海 200092；3. 同济大学 土木工程学院， 上海 200092； 4. 同济大学 航空航天与力学学院， 上海 200092)



全断面隧道掘进机破岩机理离散元分析

蒋明镜1,2,3， 孙亚1,2,3， 王华宁1,4， 袁聚云1,2,3

(1. 同济大学 土木工程防灾国家重点实验室， 上海 200092； 2. 同济大学 岩土及地下工程教育部重点实验室， 上海 200092；3. 同济大学 土木工程学院， 上海 200092； 4. 同济大学 航空航天与力学学院， 上海 200092)

摘要：将基于微观胶结试验得到的岩石微观力学模型植入离散元软件，模拟滚刀破岩过程并重点分析滚刀破岩各阶段的宏微观机理.结果表明：滚刀破岩过程按破岩阻力和侵入深度的关系可以分为3个阶段，即加载阶段、卸载阶段和残余跃进阶段；破岩过程中的胶结破坏主要分为拉破坏和剪扭破坏2种类型，其中，中裂纹主要由拉剪扭复合破坏引起，斜裂纹主要由拉破坏引起，证实了张拉破坏理论.加载阶段是滚刀破岩的必经阶段，卸载阶段是滚刀破岩的关键阶段，有效利用卸载阶段破碎特性可以提高破岩效率.

关键词：全断面隧道掘进机(TBM)； 破岩机理； 离散元模拟

伴随着西部大开发的步伐，越来越多的隧道需要在地质条件复杂的地区施工.为保证高效、安全的施工，全断面隧道掘进机(TBM)正发挥着越来越大的作用.

TBM掘进的过程是滚刀不断切割岩体的过程,因此滚刀的破岩机理一直是研究的热点问题.在20世纪70年代，Swain等[1-2]从滚刀破岩过程出发，用能量平衡和相似原理来建立裂纹长度与荷载间的关系.到80年代，国内学者余静[3]通过研究岩石破碎的发展过程建立了破岩机理模型，将破岩过程分为典型的6个阶段，并认为卸载阶段对破岩贡献最大.Sanio[4]通过对破岩机理的分析认为：张拉破坏是楔形滚动破岩的主要力学机制，并且在滚刀下存在静水压力核的现象.遗憾的是，理论研究只是根据试验结果进行一些假设，所总结的模型无法考虑破岩过程岩体内部微观信息的影响，对破岩过程无法做到更全面更深入的了解，很难具有普适性.

近几年来，随着离散元方法(discrete element method,DEM)[5]在研究材料特性微观机理方面的兴起，对滚刀破岩机理的探讨也逐渐走向全面和深入. Gong等[6-7]使用离散元方法验证了离散元模拟滚刀破岩的可行性，并进行了一系列工况的研究：岩体节理方向、节理间距及滚刀距离对破岩效率的影响.Moon等[8]通过对比室内线性切割试验和离散元模拟的结果，研究了不同滚刀间距的破岩效率.苏利军等[9]基于颗粒流方法对TBM滚刀破岩过程进行了模拟，证实了破岩的挤压-张拉破坏理论，讨论了刃角、刃宽对破岩效率的影响.张魁等[10]使用离散元软件，模拟了双刀具侵入岩石的过程，分析了围压和刀间距对破岩效率的影响.莫振泽等[11]研究了不同刃角楔形刀具破岩的全过程，认为脆性岩石材料的破坏过程是内部微裂纹的萌生和扩展的宏观反映.谭青等[12]应用离散元法研究了滚刀破岩的微观过程，探讨了刃宽、刃角对破岩效率的影响.虽然前人已广泛采用离散元方法针对滚刀破岩过程岩石的破裂模式及过程进行了诸多研究,但学者们对破岩过程中岩体裂纹扩展阶段的划分、各阶段裂纹扩展的微观机理及破岩效率的贡献研究较少，有待进一步完善.另一方面，离散元粒间接触模型的选用会直接影响到模拟结果，因而合适的微观接触模型的选择是模拟分析滚刀破岩过程至关重要的一步.

本文采用基于室内试验建立的微观胶结接触模型，通过离散元方法模拟滚刀破岩全过程，分析了各阶段破岩的微观机理及各阶段对破岩效率的影响.该模型的显著优势是解决了离散元方法采用常规模型模拟岩石材料时普遍过高估计岩石材料抗拉强度与抗压强度比值的问题[13],因此该模型可以更合理地反映岩石受荷后裂纹扩展过程以及岩质边坡失稳破坏过程[14].

1　模型介绍

本文基于室内水泥铝棒胶结试验[15]，提取了含抗转动能力的无胶结厚度岩石微观力学模型并导入了离散单元法商业软件.试验中将铝棒视为颗粒，水泥视为胶结物质，将2根相同铝棒按照特定尺寸胶结在一起，测试胶结铝棒的抗压、抗拉、抗剪、抗扭的力学特性.试验结果证实，胶结的法向荷载会显著地影响胶结物质的抗剪和抗扭特性.使用该模型模拟岩石力学性质的结果显示，该模型可以使岩石在围压增大时，强度值显著增大，这是常规接触模型无法做到的.模型的分析推导过程见文献[16]，本文只介绍相关结果.

该模型为无厚度胶结模型，其颗粒之间的力学响应分为两部分:胶结部分和颗粒部分.颗粒部分采用常规的离散元模型，胶结部分力学响应如下所示：

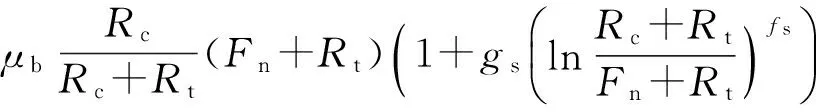
(1)

(2)

式中：Rc、Rt、Rs、Rr为胶结物的抗压、抗拉、抗剪、抗扭强度；Fn为法向力；μb为胶结物间摩擦系数；βb为胶结抗转动系数；r为颗粒等效半径；gs、fs、gr、fr为试验得到包线形状参数.

当法向力为压力，但胶结未破坏时，胶结部分和颗粒部分受力为并联状态，粒间作用力按刚度分配,强度包线如下所示：

(3)

(4)

式中：Fnb、Fnp分别为胶结物、颗粒所承担的法向力；μp为颗粒间摩擦系数；βp为颗粒抗转动系数.

当胶结发生破坏后，由于胶结物仍会存在于接触点附近，故残余强度包线如下所示：

(5)

(6)

结合以上各情况，总结强度包面[17]如图1所示.

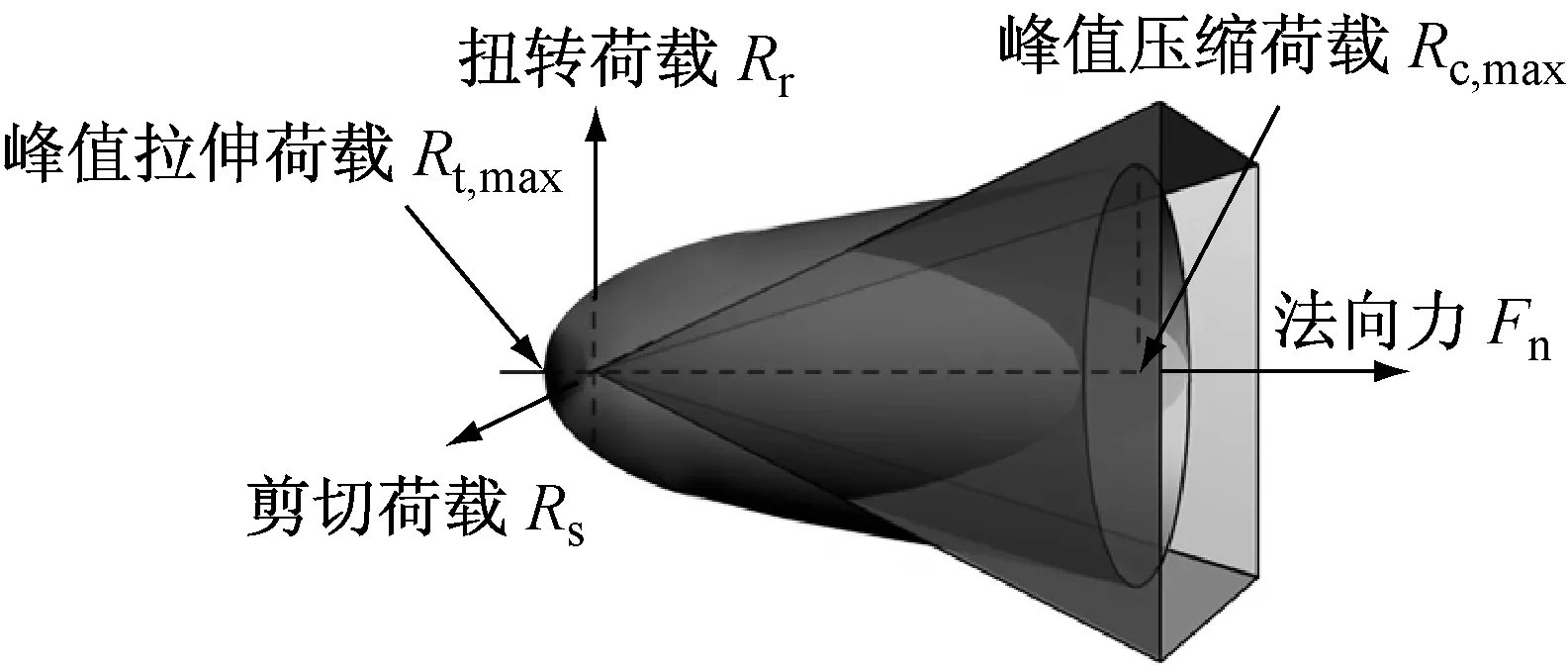
图1　无厚度有抗转动胶结模型强度包面[17]

2　TBM破岩过程模拟

2.1离散元岩石试样的力学性质

本文所使用的离散元试样的岩石性质模拟Lac du Bonnet 花岗岩[18]，属于硬脆性岩石.针对花岗岩的密实度、均匀性特性选择了如图2所示的级配曲线.模型参数的选取依照单轴压缩试验和巴西试验.其中，单轴压缩试验试样与巴西试验试样均采用Jiang等[19]提出的分层欠压法生成.DEM岩石试样单轴压缩试验时，将颗粒的胶结强度参数取得非常大，以保证颗粒之间没有发生胶结破坏，只发生弹性变形.然后，在其他参数不变的情况下，改变颗粒的刚度，通过单轴压缩试验获取DEM岩石试样的弹性模量，并与室内实测试验结果相比较，确定试样的微观胶结刚度参数；采用同样的方法，并改变颗粒的法向刚度与切向刚度的比值，通过单轴压缩试验获取DEM岩石试样泊松比，得出颗粒的法向刚度与切向刚度的比值与DEM岩石试样泊松比的关系，然后通过室内实测泊松比试验数据确定颗粒的微观刚度参数.微观刚度参数确定后，分别通过单轴压缩试验及巴西试验的试验数据来确定试样的微观胶结强度参数.本文选取0.5作为模型中胶结摩擦系数μb和抗转动系数βb的数值，按室内试验得到的颗粒与胶结摩擦系数和抗转动系数比值关系，得到颗粒的摩擦系数μp和抗转动系数βp分别为1.0和1.5.

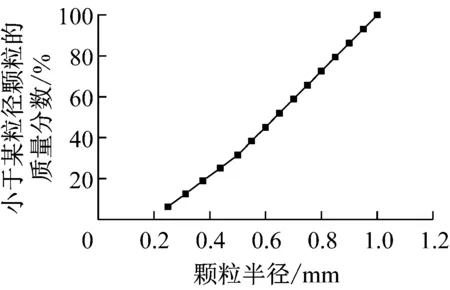
图2　颗粒级配曲线

图3为DEM岩石试样单轴压缩的试验曲线.从图中可以看到,试样表现为典型的弹脆性破坏模式，与室内试验[20]所得单轴压缩曲线相似，其单轴压缩强度为200 MPa，弹性模量为67.53 GPa，泊松比为0.256.图4为DEM岩石试样巴西试验结果经换算后的应力-应变曲线，得到拉伸强度为11.36 MPa，与室内试验结果吻合较好.据此得到DEM岩石试样的微观模型参数，如表1所示.

2.2滚刀及DEM岩石试样的形成

实际TBM施工中，与滚刀行进方向相平行的推力是滚刀切割岩体的主要作用力，同时结合前人的研究成果[21]可以得出采用二维离散元方法，将滚刀破岩过程简化为滚刀侵入岩体的平面问题是合理的.本文首先生成岩石地基试样，再生成滚刀，赋予滚刀一定的竖向速度垂直侵入DEM岩石试样，并记录侵入过程中各阶段DEM岩石试样的微观信息.本文选取的滚刀形状参数与TBM施工常用的43.18 cm常截面盘形滚刀接近，为平刃滚刀，刃宽w为15 mm，刃角α为20°，滚刀形状如图5所示.

图3　DEM岩石试样单轴压缩应力应变曲线

图4　DEM岩石试样巴西试验应力应变曲线

参数取值颗粒法向刚度Knp/(N·m-1)1.8×1011颗粒切向刚度Ksp/(N·m-1)9.47×1010胶结法向刚度Kn/(N·m-1)9.0×1010胶结切向刚度Ks/(N·m-1)4.735×1010胶结抗压强度Fn/kN8.0×104胶结抗拉强度Ft/kN65胶结摩擦系数μb0.5颗粒摩擦系数μp1.0胶结抗转动系数βb0.5颗粒抗转动系数βp1.5

DEM岩石试样形成的过程与前文所述单轴试样形成过程相似，颗粒总数为50 000，采用分层欠压法分8层生成孔隙比为0.2的地基，然后在竖向压力0.55 MPa下边固结边施加微观胶结模型，模拟自然岩石的形成过程，待平衡后，撤掉试样上部刚性墙，进行应力释放，直至试样内部速度场稳定，得到试验所用试样.试样最终尺寸为0.15 m×0.3 m，如图6所示.

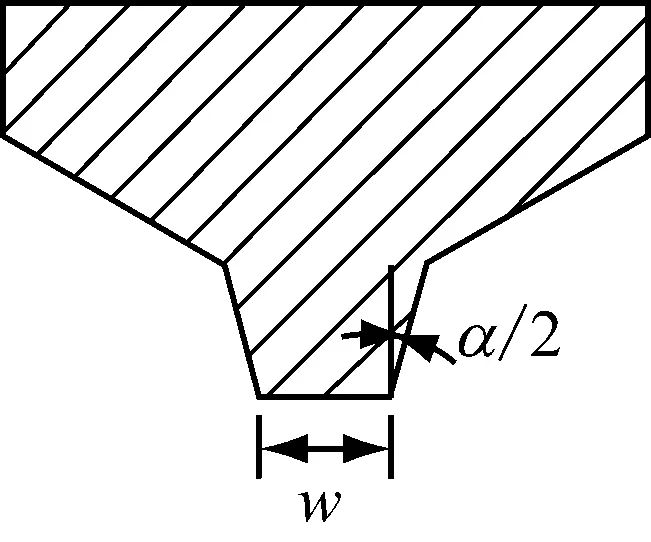
图5　滚刀示意图

3　模拟试验结果

图7为滚刀破岩过程中的法向推力(破岩阻力)与侵入深度以及胶结破坏数目关系曲线， 可以看出法向推力一开始随着侵入深度的增加急剧增加，达到峰值后迅速跌落，最后在很小的量值范围内波动；侵入过程中伴随着胶结破坏点的产生，胶结破坏点分为拉伸破坏和剪扭破坏，2种破坏模式都是一开始随着侵入深度的增加显著增加，达到一定侵入深度后都趋于稳定，且整个过程中，拉伸胶结破坏点数目多于剪扭胶结破坏点数目.

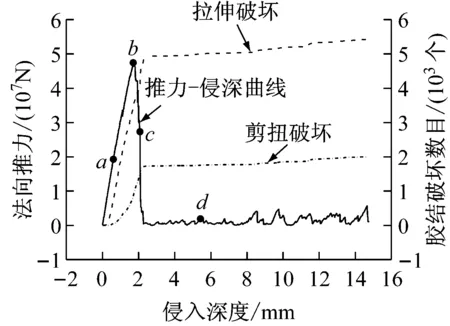
图7　　　　DEM岩石试样破岩过程法向推力侵深关系以及胶接破坏数目侵深关系

Fig.7Normal force-penetration relationship and bond breakage-penetration relationship during DEM rock cutting

根据曲线特征可以将破岩过程主要分为3个阶段：① 加载阶段.该阶段中破岩阻力几乎随侵深线性增加，直至峰值，同时胶结破坏点开始产生，且拉伸破坏点多于剪扭破坏点，说明这一阶段岩体中已经发生微裂纹扩展.② 卸载阶段.达到峰值后破岩阻力突然跌落至较小的值，产生明显的跃进现象，且这一阶段胶结破坏点数目继续增加，说明岩体内微裂纹能够继续扩展.③ 残余跃进破碎阶段.破岩阻力产生明显跌落后，该阶段破岩阻力在一个很小的范围内波动并伴随着跃进破坏现象，同时胶结破坏点趋于稳定，说明该阶段滚刀行进所受阻力很小，并且岩体内部很难再有微裂纹产生，试样已经破坏.另外，胶结拉破坏点以及剪扭破坏点虽然在破岩过程中产生的数量不同，但发展趋势较一致，说明破岩过程实际上是岩石内部拉剪扭复合破坏模式.本文模拟的侵入曲线形式与Moon等[8]的DEM岩石试样模拟结果相似，但与谭青等[12]的试验结果在跃进破碎阶段有一定差异，主要原因是：本文和Moon等[8]模拟的是硬脆性岩石，其脆性破坏特征较显著；而文献[12]中试验材料是软岩，由于单次贯入并不能造成很大的压碎面积，因而在跃进破碎阶段依然有较大阻力.

3.2裂纹扩展过程宏微观机理分析

根据前文所述破岩阻力-侵深关系曲线特性，选取曲线中加载阶段特征点a、峰值特征点b、卸载阶段特征点c，残余跃进阶段特征点d(见图7)的一系列宏微观信息特征图进行分析，揭示滚刀破岩过程微观机理.图8～11分别为破岩过程中各特征点时刻的试样图、力链图、胶结分布图及胶结破坏点分布图.

从试样图中可以看出，加载阶段整个试样保持较完整.峰值阶段亦无明显宏观裂纹产生，但滚刀已经侵入岩体一定深度，并伴随着少量颗粒弹射飞出，说明岩体中能量已经大量贮存，为大规模裂纹扩展提供必要条件.卸载阶段中试样已经出现明显宏观裂纹，裂纹发启于滚刀一侧，向自由面发展.残余跃进阶段中宏观裂纹更明显，并与自由面贯通形成岩块，可以看出该岩块由于滚刀继续侵入而被明显挤出的趋势.在实际破岩中，由于滚刀推进而产生的岩块会与相邻滚刀行进产生的岩块贯通连接形成较大岩块脱落，不必依靠滚刀继续进行挤出.图12为室内试验试样侵入试验的裂纹扩展形态，可以看出与离散元模拟结果相似，但是离散元试样的宏观裂纹更趋近于水平，这是因为离散元试样模拟的材料是强度较高的花岗岩，硬脆性较强，裂纹扩展更接近于滚刀下方的压碎区.另外，2种试验方法都出现裂纹扩展不对称的现象，这是因为室内试验岩石试样内部初始便存在诸多不规则分布的且有利于能量释放及裂纹扩展的微裂纹，从而很大程度上决定了岩石受侵入荷载后破坏模式的非对称性，而对于数值模拟模型，在裂纹扩展过程即能量释放的过程中，可能存在某一侧的胶结点更容易破坏，能量集聚释放，这种“集聚效应”的产生会进一步引发附近的更多胶结点破坏，形成宏观裂纹.综上可知，试验与模拟过程中试样内部的能量分布不均匀性导致了裂纹扩展的非对称性.

a特征点a时刻b特征点b时刻

c特征点c时刻d特征点d时刻

图8　DEM岩石试样破岩过程特征点时刻试样图

c特征点c时刻d特征点d时刻

图9DEM岩石试样破岩过程特征点时刻力链图

Fig.9Force chains in DEM rock sample at the feature points during penetration

从力链图中可以看出，在加载阶段，滚刀正下方有一个力链集中的区域，这类似于Sanio[4]所提到的静水压力核，部分力链近似与集中区域散射出的力链相垂直呈弧形分布，这与Moon等[8]所做试验得

出的现象相似，如图13所示.峰值阶段力链变化不明显，依旧呈放射状分布，且有部分力链集中于两侧发展，特别在滚刀下方两侧局部区域.卸载阶段中，由于裂纹的产生力链集中现象消失，在裂缝处存在力链明显集中分布.残余跃进阶段中的力链分布与卸载阶段相似，但能够观察到力链浓度减少，说明卸载阶段到残余掘进阶段发生的岩块产生、挤出的过程，主要是岩体内部应力消散过程，而岩体内部颗粒相互作用形式未发生较大改变.

胶结分布图中黑色代表胶结部分，白色为胶结破坏部分.结合胶结破坏点分布图可以看出，加载阶段中，胶结分布图中无明显裂纹，但已有胶结破坏点(微裂纹)产生且主要集中在滚刀下方(中裂纹)，由力链图可知，这一阶段滚刀下方应力集中，在破岩过程中首先出现胶结破坏点.峰值阶段从胶结分布图中可以看出明显裂纹，裂纹主要分布于滚刀正下方，并有少量斜裂纹产生，从破坏点分布图中可以看出这一阶段滚刀下方破坏点明显增多，开始形成中裂纹和斜裂纹.卸载阶段可以看出裂纹继续扩展，胶结破坏点继续增多，这种趋势与前文所述一致，并且斜裂纹充分向自由面发展.残余跃进阶段中可以看出裂纹数目没有显著发展，与前文所述一致，胶结破坏点不再继续增加，说明残余阶段岩石内部应力水平趋于稳定.从胶结破坏点产生的整个过程可以看出,中裂纹产生是斜裂纹产生的基础，岩体受滚刀侵入而积聚的能量首先倾向于在滚刀下方释放，随后转向两侧释放，因此研究斜裂纹萌生的初始能量条件，更合理地分配TBM掘进时的推力值可以大大提高TBM工作效率.

a特征点a时刻b特征点b时刻

c特征点c时刻d特征点d时刻

图10　DEM岩石试样破岩过程特征点时刻胶结分布图

c特征点c时刻d特征点d时刻

图11DEM岩石试样破岩过程特征点时刻胶结破坏点分布图

Fig.11Bond breakage distributons in DEM rock sample at the feature points during penetration

图12　室内侵入试验岩石破坏形态[9]

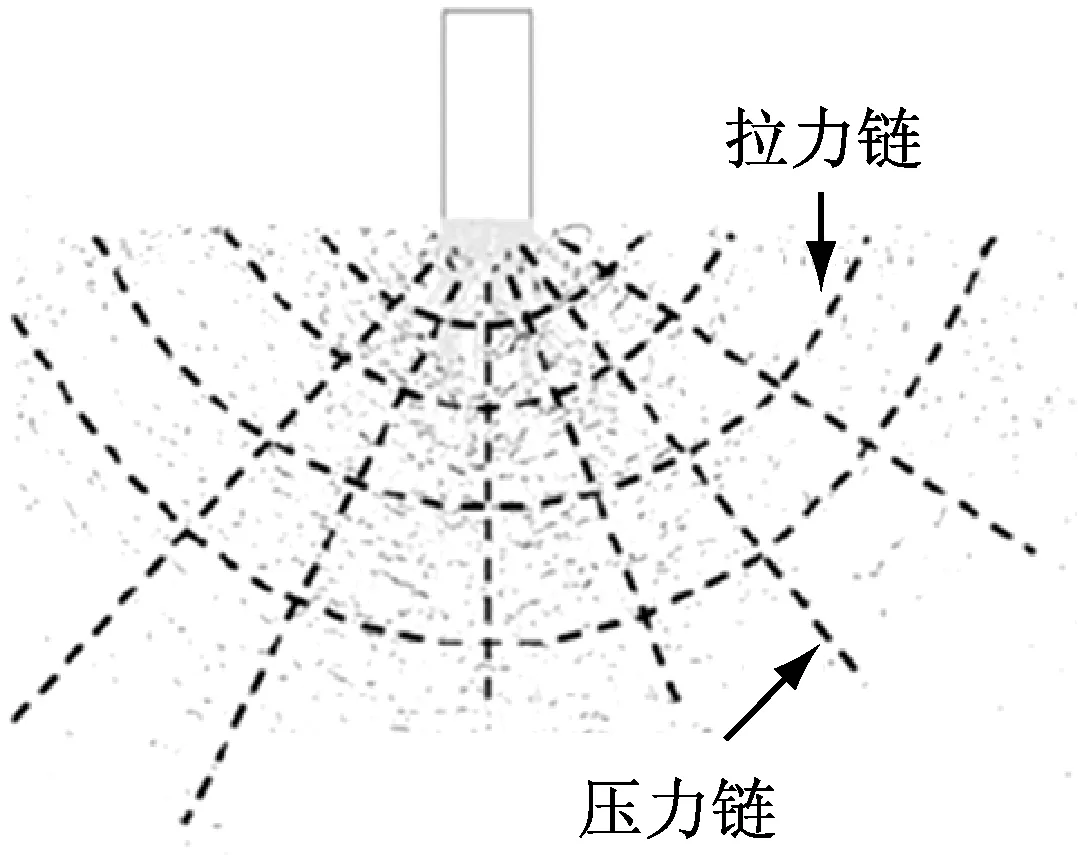
图13　DEM岩石试样中的力链分布[8]

4　与经典破岩机理对比及讨论

Swain等[1-2]提出的侵入理论认为，加载时岩石出现径向的赫兹裂纹，卸载时才出现横向裂纹，这与本文模拟结果一致.

余静[3]认为破岩过程中产生的岩体主要由拉伸应力引起并将滚刀破岩过程分为典型的6个阶段，表现为能量的积聚与释放，与本文模拟结果相似.另外，该文献中还指出卸载阶段破岩量占整个过程的80%以上，是破岩过程的主要阶段.图14为本文模

拟的加载及卸载过程中总胶结破坏点及有效贯通胶结破坏点产生数目，其中总胶结破坏点是指岩石内部所有胶结破坏点，有效贯通胶结破坏点是指岩石内部离刀刃中心水平方向3倍刃宽及以上距离的胶结破坏点，表征的是边裂纹的扩展能力.可以看出，卸载过程中产生的胶结破坏点总数要少于加载阶段产生的胶结破坏点总数，与文献所述并不一致，但有效贯通胶结破坏点总数要明显多于加载阶段产生的有效贯通胶结破坏点总数，从而有效贯通胶结破坏点产生率大于加载阶段.根据前文所述，加载阶段胶结破坏点主要产生于滚刀下方，卸载阶段才是出现斜裂纹(有效裂纹)扩展的主要阶段，这一现象再次被离散元模拟过程中所得微观信息证实，而在滚刀破岩过程中，斜裂纹的有效扩展才是保证岩体被顺利切割的关键.因此，卸载过程是滚刀破岩过程的关键阶段，利用好卸载阶段的破碎作用会大大提高破岩效率.但是另一方面，卸载阶段斜裂纹的顺利扩展要以加载阶段滚刀下方胶结破坏点集聚破坏为前提，而加载过程结束时可能使得岩体内部已经存在大量微裂纹.综上所述，卸载过程是滚刀破岩的关键阶段，而加载过程是必经阶段，但岩体在卸载阶段产生总微裂纹数目并不一定比加载阶段产生的多，但有效贯通微裂纹数目多于加载阶段所产生数目.

a 总胶结破坏点

b 有效贯通胶结破坏点

5　结论

(1) 滚刀破岩的力学响应分为3个阶段：加载阶段、卸载阶段和残余跃进破碎阶段.

(2) 胶结破坏点会在加载阶段和卸载阶段都大量产生，在残余跃进破碎阶段趋于稳定.加载阶段，胶结破坏点主要聚集在滚刀下方，形成中裂纹，为拉剪扭复合破坏模式；卸载阶段，胶结破坏点主要聚集在滚刀两侧位置，形成斜裂纹，主要为拉伸破坏.

(3) 加载阶段是破岩过程中的必经阶段，卸载过程是关键阶段，卸载过程中有效裂纹的扩展效率大于加载阶段，利用好卸载阶段的破碎作用可以提高工程效率.

参考文献:

[1]Swain M V, Hagan J T. Indentation plasticity and the ensuing fracture of glass[J]. Journal of Physics D: Applied Physics, 1976, 9(15): 2201.

[2]Swain M V, Lawn B R. Indentation fracture in brittle rocks and glasses[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1976, 13(11): 311.

[3]余静. 岩石机械破碎规律和破岩机理模型[J]. 煤炭学报, 1982, 7(3): 10.

YU Jing. Rules of rock fragmentation with mechanical methods and model of rock failure mechanism[J]. Journal of China Coal Society, 1982, 7(3): 10.

[4]Sanio H P. Prediction of the performance of disc cutters in anisotropic rock[J]. International Journal of Rock Mechanics and Mining Science & Geomechanics Abstracts, 1985, 22(3): 153.

[5]Cundall P A, Strack O D L. A discrete numerical model for granular assemblies[J]. Geotechnique, 1979, 29(1): 47.

[6]Gong Q M, Zhao J, Jiao Y Y. Numerical modeling of the effects of joint orientation on rock fragmentation by TBM cutters[J]. Tunneling and Underground Space Technology, 2005, 20(2): 183.

[7]Gong Q M, Jiao J J, Zhao J. Numerical modeling of the effects of joint spacing on rock fragmentation by TBM cutters[J]. Tunneling and Underground Space Technology, 2006, 21(1): 46.

[8]Moon T, Oh J. A study of optimal rock-cutting conditions for hard rock TBM using the discrete element method[J]. Rock Mechanics and Rock Engineering, 2012, 45: 837.

[9]苏利军, 孙金山, 卢文波. 基于颗粒流模型的TBM滚刀破岩过程数值模拟研究[J]. 岩土力学, 2009, 30(9): 2823.

SU Lijun, SUN Jinshan, LU Wenbo. Research on numerical simulation of rock fragmentation by TBM cutters using particle flow method[J]. Rock and Soil Mechanics, 2009, 30(9): 2823.

[10]张魁, 夏毅敏, 谭青, 等. 不同围压条件下TBM刀具破岩模式的数值研究[J]. 岩土工程学报, 2010, 32(11): 1780.

ZHANG Kui, XIA Yimin, TAN Qing,etal. Numerical study on modes of breaking rock by TBM cutter under different confining pressure[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(11): 1780.

[11]莫振泽, 李海波, 周青春, 等. 基于UDEC的隧道掘进机滚刀破岩数值模拟研究[J]. 岩土力学，2012, 33(4)： 1196.

MO Zhenze, LI Haibo, ZHOU Qingchun,etal. Experimental study of rock microscopic deterioration under wedge cutter[J]. Rock and Soil Mechanics, 2012, 33(4): 1196.

[12]谭青, 李建芳, 夏毅敏, 等. 盘形滚刀破岩过程的数值研究[J]. 岩土力学, 2013, 34(9): 2707.

TAN Qing, LI Jianfang, XIA Yimin,etal. Numerical research on rock fragmentation process by disc cutter[J]. Rock and Soil Mechanics, 2013, 34(9): 2707.

[13]Jiang M J, Chen H, Crosta G B. Numerical modeling of rock mechanical behavior and fracture propagation by a new bond contact model[J]. International Journal of Rock Mechanics & Mining Sciences, 2015, 78:175.

[14]Jiang M J, Jiang T, Crosta G B,etal. Modeling failure of jointed rock slope with two main joint sets using a novel DEM bond contact model[J]. Engineering Geology, 2015, 193:79.

[15]Jiang M J, Sun Y G, Xiao Y. An experimental investigation on the contact behavior between cemented granules[J]. Geotechnical and Testing Journal, 2012, 35(5): 678.

[16]蒋明镜, 白闰平, 刘静德, 等. 岩石微观颗粒接触特性的试验研究[J]. 岩石力学与工程学报, 2013, 32(6): 1121.

JIANG Mingjing, BAI Runping, LIU Jingde,etal. Experimental study of inter-granular particles bonding behaviors for rock microstructure[J]. Chinese Journal of Rock Mechanics and Engineering , 2013, 32(6):1121.

[17]陈贺. 岩石宏微观力学特性及高陡岩质边坡的离散元数值模拟[ D]. 上海: 同济大学, 2013.

CHEN He. Macro- and micro- mechanical behaviors of rock and simulation of high-steep rock slope by distinct element method[D]. Shanghai: Tongji University, 2013.

[18]Meglis I L, Chow T M, Young R P. Progressive microcrack development in tests on Lac du Bonnet Granite. I. acoustic emission source location and velocity measurements[J]. International Journal of Rock Mechanics Sciences and Geomechanics Abstract, 1995, 32(8): 741.

[19]Jiang M J, Konrad J M, Leroueil S. An efficient technique for generating homogeneous specimens for DEM studies[J]. Computers and Geotechnics, 2003, 30(7): 579.

[20]Martin C D. The strength of massive Lac du Bonnet granite around underground openings[D]. Winnipeg: University of Manitoba, 1993.

[21]Innaurato N, Oggeri C, Oreste P P,etal. Experimental and numerical studies on rock breaking with TBM tools under high stress confinement[J]. Rock Mechanics and Rock Engineering, 2007, 40(5): 429.

收稿日期：2015-08-31

基金项目：国家“九七三”重点基础研究发展计划(2011CB013504, 2014CB046901)

中图分类号：TU452

文献标志码：A

Rock Failure Mechanism Analysis With Discrete Element Method by Using Tunnel Boring Machine

JIANG Mingjing1,2,3， SUN Ya1,2,3， WANG Huaning1,4， YUAN Juyun1,2,3

(1. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China; 2. Key Laboratory of Geotechnical and Underground Engineering of the Ministry of Education, Tongji University, Shanghai 200092, China；3. College of Civil Engineering, Tongji University, Shanghai 200092, China; 4. School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200092, China)

Abstract：The process of rock cutting was simulated by discrete element method software where the reasonable contact model for rock summarized from the micro bond contact experiment was implanted. The macroscopic and microscopic mechanism on the crack propagation of each stage during rock cutting was investigated. The results show that: the process of rock cutting can be divided into three stages, i.e. loading stage, unloading stage and residual leaping broken stage; failures of the bonds mainly exhibit tensile failure and shear-torsion failure. The crack under the tip is mainly caused by shear-torsion failures while oblique crack is mainly caused by tensile failures. Therefore, the tension failure theory was confirmed. The unloading stage is the critical stage of the overall process and the efficiency of rock fragmentation will be improved if the fragmentation behavior of unloading stage is efficiently used.

Key words：tunnel boring machine(TBM)； rock failure mechanism； discrete element method simulation

第一作者： 蒋明镜(1965—)，男，教授，博士生导师，工学博士，主要研究方向为天然结构性黏土、砂土、太空土、深海能源土、非饱和土的宏微观试验、本构模型和数值分析以及土体逐渐破坏分析.E-mail:mingjingjiang@tongji.edu.cn