燃料棒径向温度场稳态计算分析

齐航，周蓝宇，张雍良，曾文杰（南华大学 核科学技术学院，湖南衡阳 421001）



燃料棒径向温度场稳态计算分析

齐航，周蓝宇，张雍良，曾文杰
（南华大学 核科学技术学院，湖南衡阳 421001）

摘要：燃料棒是反应堆的核心部件，其内部温度场分布大都通过数值计算获得。以燃料棒为研究对象，以燃料棒中心为起点，在径向上划分足够多的环形区域，建立几何模型，依据几何模型建立堆芯稳态物理模型，通过编程进行数值计算来获得燃料元件的径向稳态温度场。以次临界堆MYRRHA的燃料棒为研究对象，研究结果表明该方法能较准确的表征燃料元件径向稳态温度场的情况，是一种简单有效的建模分析方法。可见，该模型可以为燃料元件径向稳态温度场计算提供合理的依据。

关键词：燃料棒；径向；温度场；稳态

本文引用格式：齐航，周蓝宇，张雍良，等.燃料棒径向温度场稳态计算分析［J］.新型工业化，2016，6（6）：17-22.

Citation： QI Hang， ZHOU Lan-yu， ZHANG Yong-liang， et al.Calculation and Analysis of the Radial Temperature Field of the Fuel Rods［J］.The Journal of New Industrialization，2016，6（6）： 17-22.

0 引言

反应堆是一种能在可控方式下实现自持链式核反应的装置，它包括了反应堆堆芯、冷却剂系统、蒸汽和动力转换系统以及其他一些系统［1］。燃料元件是核反应堆中装载核燃料并在运行时释放出能量的部件，是核反应堆安全的第一道屏障，而燃料元件温度是影响燃料元件性能的决定性因素之一，因此开展燃料元件径向稳态温度场研究尤为必要。而燃料元件内部温度场分布无法使用探测器直接测量得到，大都是通过数值计算获得。

目前国内外都开展了很多关于燃料元件稳态温度计算的研究，提出了相应的计算模型。S.Heusdains［2］以MYRRHA为研究对象，将堆芯燃料组件划分出热通道、中热通道和冷通道三个子通道，计算出了稳态条件下燃料元件在径向上的温度分布。韩骞［3］等人以中国铅基实验堆（CLEAR-I）为研究对象，利用有限元分析程序ANSYS对该堆的燃料元件活性区在正常运行工况和失流事故下的温度场进行了数值模拟与分析。梁志滔［4］以900MW压水堆核电站堆芯为模拟对象，计算得到燃料元件上不同高度处的温度，其结果与该压水堆运行的实际数据基本一致。

本文以MYRRHA反应堆棒状燃料元件为研究对象，采用划分环形区域的建模方法，通过数值计算来获取燃料元件径向稳态温度场；计算结果与文献基本吻合，从而证实了模型的有效性。

1 模型

1.1 模型假设

燃料元件内燃料芯块发生核裂变释放的能量通过间隙氦气传递到包壳，然后经过冷却剂与包壳外表面之间的对流换热将热量传递至冷却剂中，传热过程中涉及到很多的物理参数及其结构参数的变化，因此需要进行合理的假设。在此基础上，建立各个部分的稳态温度分布模型。假设条件［5-6］：

（1）仅考虑填充芯块、气体和包壳之间的热传导，不考虑热辐射效应；

（2）仅在包壳表面与冷却剂换热，忽略燃料元件的轴向传热；

（3）芯块和包壳处于同心状态；

（4）燃料棒芯块内的每个轴向节块是均匀发热；

（5）芯块和包壳之间间隙是纯氦气，即不考虑其他裂变气体对间隙氦气热导率的影响。

1.2 模型

1.2.1 几何模型

以燃料棒中心为起点，首先在径向上按照半径等分法划分足够多的环形区域，然后再在每一个环形区域内按照面积加权法取一个平均半径，并且用这个平均半径上的温度值表示环形区域的平均温度，如图1所示。T1、T2……所在的位置为相应环形区域的平均半径位置处，Tr为冷却剂LBE的温度值。Rn为燃料芯块的外半径， Rn +1为包壳的内半径， Rn+ m为包壳的外径。每一个环形区域的平均半径由下式计算出：

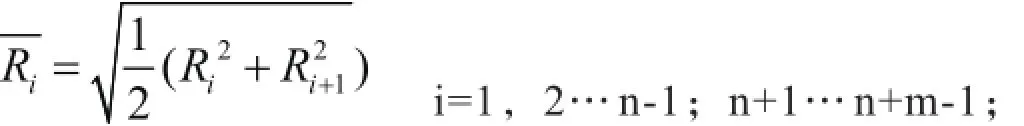
Ri和 Ri+1分别为环形区域的内外半径，单位：m。

1.2.2 传热模型

燃料芯块：由于燃料区轴向导热远小于径向导热，故忽略燃料的轴向导热。稳态能量守恒方程为：

式中：qv为热功率，w/m3；r为半径，m；ku为MOX燃料热导率，w/（m·K）；T为温度，K。

包壳内部：包壳区属于非燃料区域，在包壳内部同燃料芯块一样，也可以划分若干个环形区域，其稳态计算能量守恒方程为：

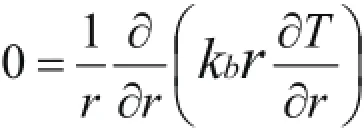
式中：kb为包壳的热导率，w/（m·K）。

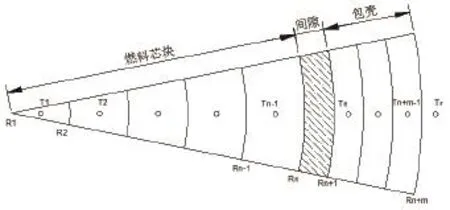
图1 燃料棒径向划分俯视图Fig.1 Top view of fuel rod in Radial partition

2 数值计算

2.1 计算

方程（1）改写为：

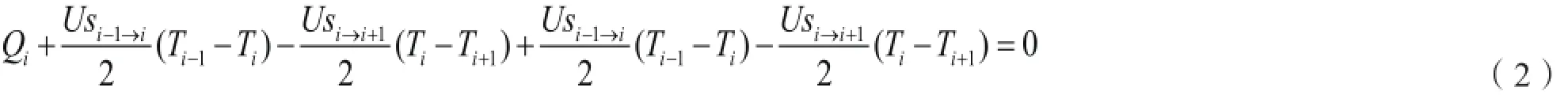
式中i为径向位置，Qi为节点环形栅元内释热率，w/m；Us为：

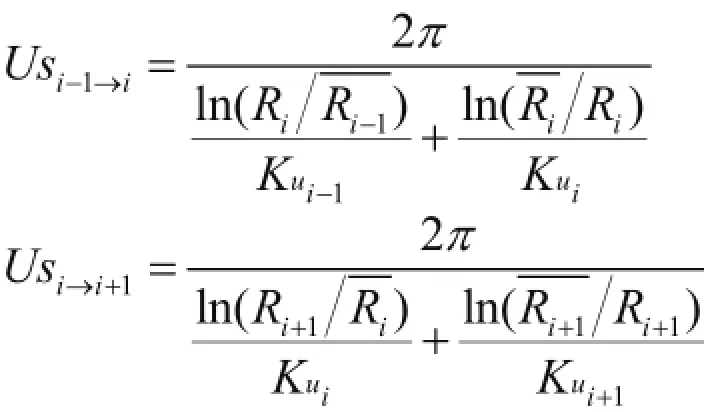
Usi-1→i和 Usi→i +1分别为节点之间的热阻，w/（m·K），如图2所示：

管道是由各种管件组装成一条满足某一特定介质输送要求的管子，并固定在一特定位置，根据BIM模型，考滤实际安装条件，即将管道按一定的长度(一般为3～8m)分节，每一节采用一个框架进行固定，该框架内组合管道即构成一节管。施工时只需将每一节管运至现场定位安装，即可一次性完成一个3～8m管道的安装。这种施工方式可以大大减少现场作业人员数量，提高管道的安装效率与质量，更有效降低施工危险性[5]。

在燃料芯块表面、包壳间隙、包壳节点及冷却剂节点上，导热热阻需要特殊处理。图3中各节点之间导热Ufc、Ub1、UL分别由下列各式计算：

a.燃料和包壳界面处传热：

式中：Rn-1表示燃料芯块最后一个环的平均半径，m； Kun-1表示燃料芯块最后一个环的热导率，w/（m·K）；Hg表示间隙氦气的换热系数［7］，10000w/（m2·K）；Rn +1表示包壳第一个环的平均半径，m；Kbn +1表示包壳第一个环的热导率，w/（m·K）；Ufc表示从最后一个燃料环进入第一个包壳环的热阻，w/（m·K）。

b.包壳外表面与冷却剂LBE间的传热：

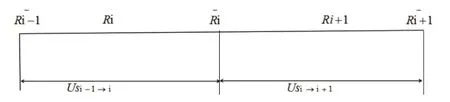
图2 节点之间的热阻简化图Fig.2 Simplified diagram of Us between nodes

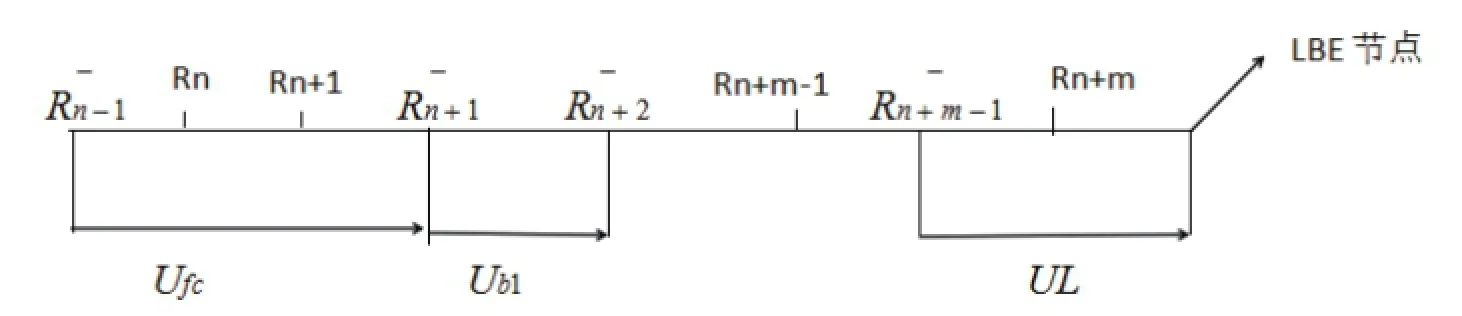
图3 燃料表面、间隙、包壳及冷却剂节点导热热阻的简化图Fig.3 Simplified diagram of Us in Fuel surface，clearance，shell and coolant node

式中：Rn+ m-1表示包壳最后一个环的平均半径，m；K bn+ m-1表示包壳最后一个环的热导率，w/（m·K）；hl表示包壳与冷却剂的换热系数，w/（m2·K）；UL表示从包壳最后一个环进入冷却剂的热组，w/（m·K）。

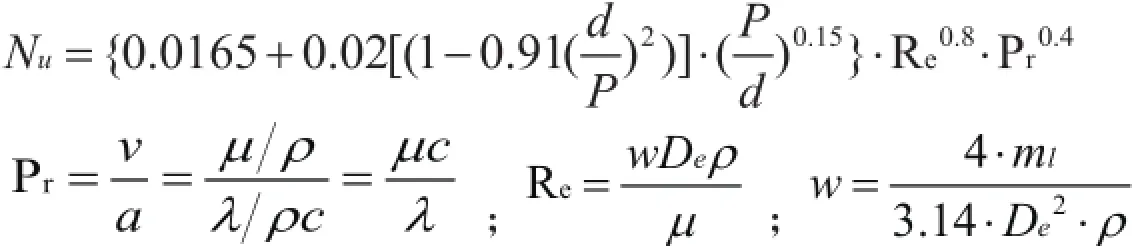
采用三角形栅格［8］（图4），则：

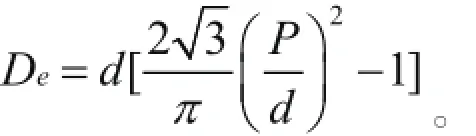
式中：Re为雷诺数；P为燃料棒之间栅距，m；d为燃料棒直径，m；w为LBE的流速，m/s；ml为LBE的质量流量，kg/s；c为LBE的定比压热容，J/（kg·K）；ρ为LBE的密度，kg/m3；v为运动粘度，m2/s，μ为动力粘度，Pa·s。

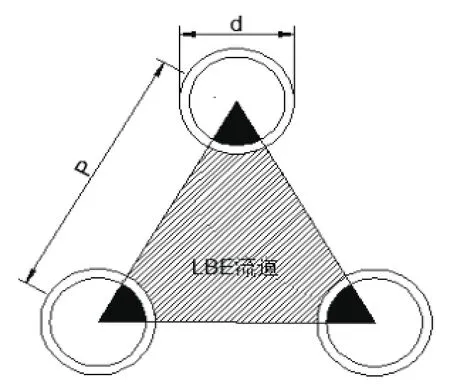
图4 三角形栅格Fig.4 Triangular lattice

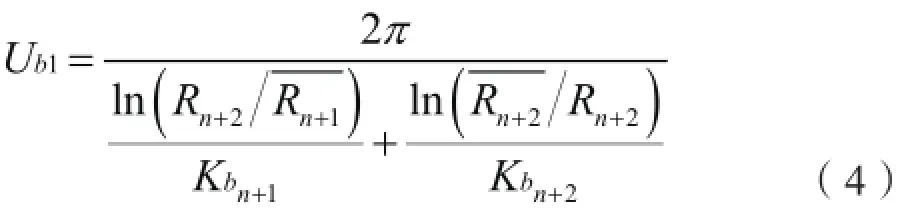
燃料芯块与包壳之间、包壳与冷却剂之间传热分别通过使（2）式中Us等于Ufc、UL得到，包壳内部节点之间的传热用Ub1、Ub2……代替。

将（2）变形可得：

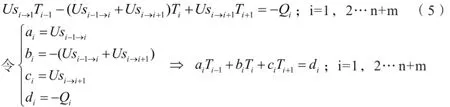
方程组中有 n+m+2 个未知数T，但只有 n+m 个方程。这样就需要两个边界条件：

1） i=1时，T0为燃料芯块中心温度，利用芯块中心绝热条件，即令：T0=T1；

2） i=n+m时， Tn+ m +1= Tr为冷却剂的温度，此温度作为已知条件，Tr=470K。

这样可以得到如下线性方程组：

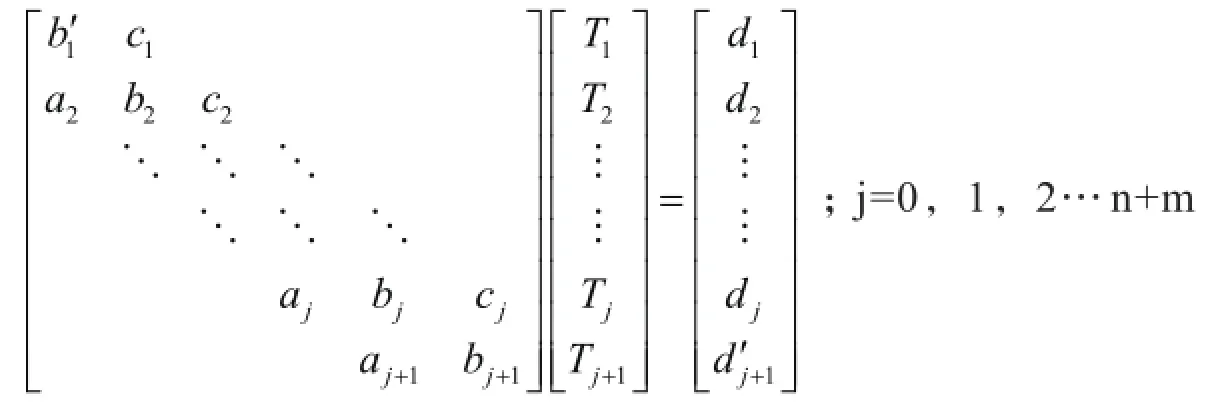
为方便与文献［1］中的结论比较，在处理过程中将燃料芯块划分为五个环形区域，间隙无划分区域，包壳划分为三个区域，则划分后实际为8×8方程组，首先给定LBE的进口温度，并且假定每个节点的温度值Ti，依据这些假定温度值便可以计算出每个节点的热导率Ki，从而求出Us，再代入方程组的系数矩阵中，求解方程组得到Ti′；比较计算出的节点温度Ti′与假定值Ti，若两者相差小于1℃，就停止计算，输出计算结果；若两者差值大于1℃，就回代求解出每个节点的热导率，再重复进行计算，多次回代，直到每个节点的前后温差小于1℃为止，即图5所示。

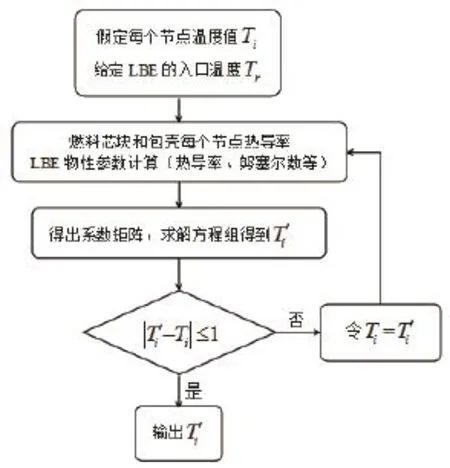
图5 流程图Fig.5 Flow chart

2.2 计算分析

依据上述计算流程编程，对MYRRHA堆棒状燃料元件进行计算。MYRRHA堆中采用棒状燃料元件，燃料芯块为MOX燃料，包壳采用T91马氏体耐热钢。在表1中列出了其燃料元件部分设计参数。

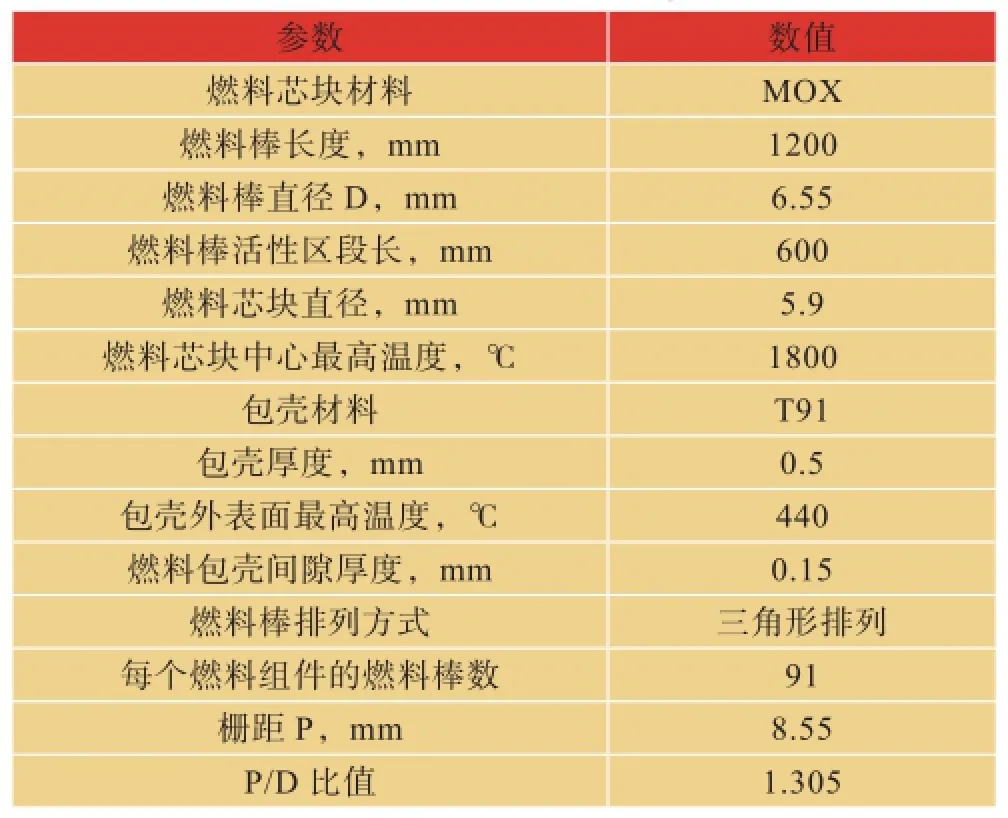
表1 MYRRHA燃料元件设计参数［8］Tab.1 MYRRHA fuel element design parameters

根据文献［1］，将MYRRHA燃料组件分为热通道、中热通道以及冷通道三种燃料组件，采用文献中的流量分配以及功率分配，通过改变冷却剂LBE的质量和系数矩阵分别计算了不同通道处的燃料元件在活性区低端的径向稳态温度场分布。

从图6、7和8中，可观察得到，相比于文献值计算值偏小，其中芯块节点5处计算值与文献值相差较大；包壳内部节点6、7、8的温度计算值无明显变化。

3 结论

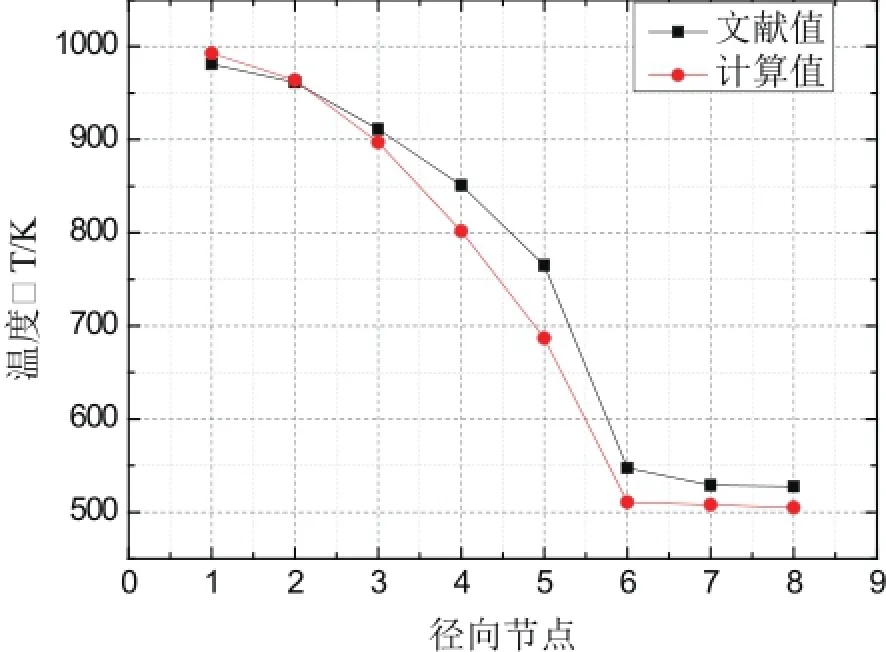
图6 燃料棒径向温度节点图（热通道）Fig.6 Fuel rod radial temperature graph（hot channel fuel）

本论文以MYRRHA堆棒状燃料元件为研究对象，研究燃料棒径向稳态温度场分布。具体是在燃料棒任一横截面上做同心圆，沿半径方向将燃料棒划分成若干环形区域，建立各区域间的传热模型，最后通过数值计算、程序编写获得堆芯燃料元件的径向稳态温度场。结果表明：该模型和计算方法在一定程度上简单有效。比较模型计算值与文献值，虽然在计算数值上并不完全相同，有百分之四左右的相对误差，但在数值变化趋势上与文献符合较好，能准确的描述燃料棒径向稳态温度场的情况。从而证实了该种模型的有效性，为燃料元件径向稳态温度场计算分析提供了一种简单有效的建模方法。

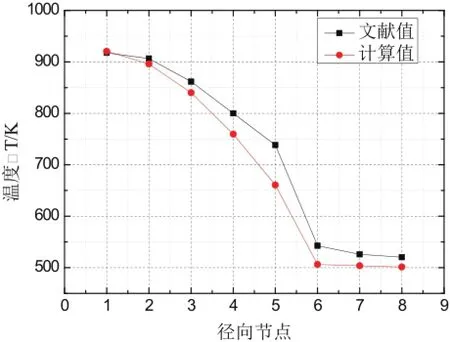
图7 燃料棒径向温度节点图（中热通道）Fig.7 Fuel rod radial temperature graph （medium channel fuel）

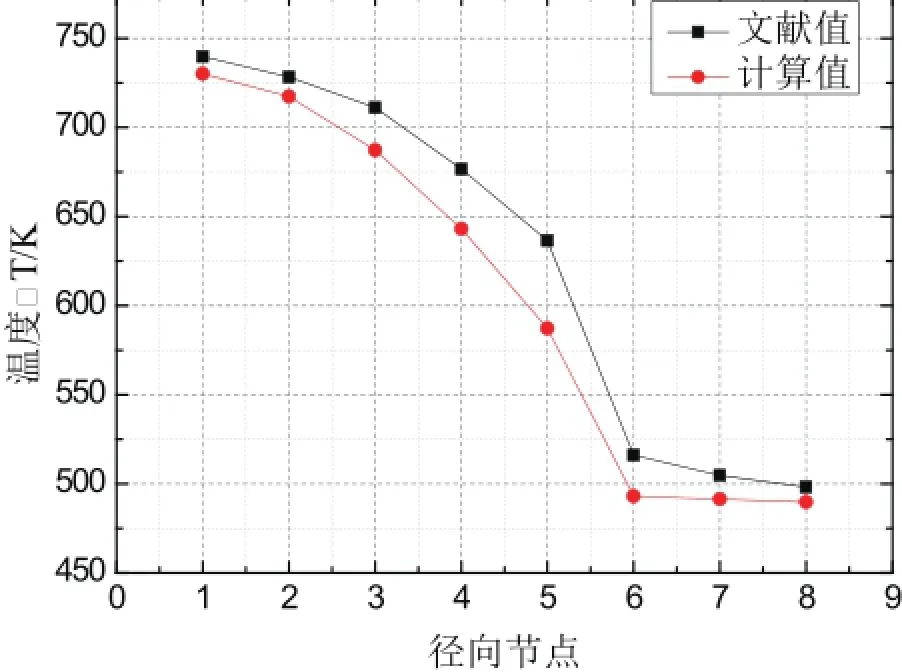
图8 燃料棒径向温度节点图（冷通道）Fig.8 Fuel rod radial temperature graph （cold channel fuel）

该模型建立在一定假设条件之上，例如不考虑轴向传热，热导率理论化等，这容易产生误差，例如即使在相同区域，也会存在材料密度和杂质含量差异以及边缘效应，因此热导率会发生相应变化。为进一步精确计算径向稳态温度场，可从假设入手改进或将燃料元件［9］、包壳以及之间的间隙划分更多的环形区域，采用更为精确的经验公式来获得径向稳态温度场。

参考文献

［1］ 陈宝山.轻水堆燃料元件［M］.化学工业出版社，2007.B S Chen，LWR fuel element［M］.Chemical Industry Press，2007.

［2］ S.Heusdains，B.Arien.Application of the RELAP5/Pb-Bi code to safety studies for the ADS MYRRHA facility［A］.Seventh information exchange meeting on actinide and fission product and transmutation［C］.NEA，2002： 1073-1085.

［3］ 韩骞，吴庆生，陈建伟，等.中国铅基研究实验堆燃料元件活性区温度场计算分析［J］.原子能科学技术，2015，49（S1）：353-359.Q Han，Q S Wu，J W Chen.Calculation and analysis of temperature field in the active region of the fuel element in the study of China's lead base［J］.Atomic Energy Science and Technology，2015，49（S1）： 353-359.

［4］ 梁志滔.压水堆核电站堆芯子通道分析［D］.华南理工大学，2011.Z T Liang.Analysis of PWR nuclear power plant reactor core channel［D］.South China University of Technology，2011.

［5］ 曾文杰，李志锋.CLEAR-IB反应堆一回路系统稳态分析［J］.新型工业化，2015，5（2）：15-16.W J Zeng，Z F Li.The Analysis of the Primary Circuit System Steady State of the CLEAR-IB Reactor［J］.The Journal of New Industrialization，2015，5（2）： 15-16.

［6］ 青涛，陈平，庞华，等.不同芯块和包壳状态下燃料棒温度场的数值模拟［J］.科技创新导报，2015（22）：81-85.T Qing，P Chen，H Pang.Numerical simulation of temperature field of fuel rod with different core and shell［J］.Science and Technology Innovation Herald，2015（22）： 81-85.

［7］ 曾文杰，赵福宇.铅铋冷快堆堆芯轴向一维单通道稳态分析［J］.新型工业化，2013（6）：14-24.W J Zeng，F Y Zhao.Analysis of core axial one-dimensional single channel steady lead bismuth cooled fast reactor［J］.The Journal of New Industrialization，2013（6）： 14-24.

［8］ H.Ait Abderrahim，V.Sobolev，E.Malambu，Fuel design for the experimental ADS MYRRHA，Technical Meeting on use of LEU，October 10-12，Vinna，Austria，2005.

［9］ 谢光善，张汝娴.快中子堆燃料元件［M］.北京：化学工业出版社，2007.G S Xie，R X Zhang.Fast reactor fuel element［M］.Beijing： Chemical Industry Press，2007.

DOI：10.19335/j.cnki.2095-6649.2016.06.003

基金项目：湖南省教育厅项目（15C1176），衡阳市科技局项目（2015KG53）

作者简介：齐航（1994-），男，本科，南华大学核科学技术学院；周蓝宇（1995-），女，本科，南华大学核科学技术学院；张雍良（1993-），男，本科，南华大学核科学技术学院；曾文杰（1988-），男，硕士，南华大学核科学技术学院

Calculation and Analysis of the Radial Temperature Field of the Fuel Rods

QI Hang， ZHOU Lan-yu， ZHANG Yong-liang， ZENG Wen-jie
（School of Nuclear Science and Technology， University of South China， Hengyang 421001， China）

ABSTRACT：Fuel rods is the core component of the reactor， often， its inner temperature field distribution is obtained through numerical calculation method.Taking the fuel rod as the research object， the center of the fuel rod as the starting point，division enough annular region in the radial， and the geometric model is set up， according to the geometric model building reactor core steady-state physical model， apply numerical calculation and programming to obtain fuel element radial steadystate temperature field.Sub-critical reactor MYRRHA fuel element as the research object.The results show that the method can accurately characterize the radial temperature field of the cylindrical fuel element， and it is a simple and effective modeling and analysis method.It can be seen that the model can provide a reasonable basis for calculating the radial temperature field of the cylindrical fuel element.

KEyWORDS：Fuel rods； Radial； Temperature field； Steady-state