离散时间切换双时标系统的建模与状态反馈控制

陈旋，陈金香（内蒙古工业大学 电力学院，内蒙古呼和浩特010080）



离散时间切换双时标系统的建模与状态反馈控制

陈旋，陈金香
（内蒙古工业大学 电力学院，内蒙古呼和浩特010080）

摘要：针对一类参数不确定性的线性离散时间双时标系统，将奇异摄动理论和切换理论相结合，建立离散时间切换双时标系统（DSTTSs）动态模型，切换理论的引入主要解决系统中参数不确定性部分对系统模型精确度的影响。主要讨论了离散时间双时标切换系统的稳定性分析以及状态反馈控制器的设计问题。利用谱范数法和线性矩阵不等式（LMIs）方法，将上述一系列问题都将归结为求解与摄动参数ε无关的线性矩阵不等式，并采用实例仿真证明该方法的有效性。

关键词：离散时间双时标系统；参数不确定性谱范数；状态反馈；线性矩阵不等式（LMIs）

本文引用格式：陈旋，陈金香.离散时间切换双时标系统的建模与状态反馈控制［J］.新型工业化，2016，6（6）：11-16.

Citation： CHEN Xuan， CHEN Jin-xiang.Modeling and State Feedback Control of Discrete-time Singularly Perturbed Systems［J］.The Journal of New Industrialization，2016，6（6）： 11-16.

0 引言

系统变量呈现慢、快两种时标特性的双时标系统广泛存在于实际控制系统，因其快时标特性影响，此类系统的建模与控制均比常规系统复杂［1］。20世纪60年代Klimushev提出的奇异摄动理论成为解决双时标问题的有效工具。

目前，对奇异摄动系统的研究成果很多，文献［2-4］论述了奇异摄动系统的稳定性，文献［5-7］对奇异摄动系统的控制器设计也做了深入研究，在实际系统中，由于工作环境的突然变化，系统元部件磨损老化等因素会导致系统参数发生变化，以往的研究成果大多数未考虑系统参数变化对系统模型的精确度的影响，进而不能得到更好的控制精度。而且大多数研究仅局限于连续时间域，假设条件较多增加了结果的保守性。近年来，对复杂系统参数不确定性的研究也不断涌出，但成果较少。文献［8-10］论述了切换奇异摄动系统的稳定性，该复杂系统由若干子系统组成，并未对不确定性部分进行详细描述，增加了系统的保守性。文献［11］论述了非线性系统中含有不确定性参数的切换控制器的设计，文中对对系统参数不确定部分进行了详细分析。文献［12］ 论述了含有参数不确定性的非线性系统的切换模糊动态输出反馈H∞控制器设计。综上，以往研究大多针对于连续时间切换系统，对离散时间复杂系统的研究较少，近年来，离散时间双时标系统的研究吸引了很多学者的关注，但是成果并非丰富，文献［13，14］分别论述了离散时间奇异摄动无时延和有时延时的稳定性。文献［15］对离散时间不确定奇异摄动系统的控制进行深入的研究，将系统分为快慢子系统分别设计控制器进行控制。综上，以往研究对离散时间双时标参数不确定性系统研究还未成形，本文的创新点在于首次提出了对含有系统参数不确定性的离散时间双时标切换系统控制问题的解决方法，在本文中，我们假设系统不确定性参数是时变的且有界，采用切换理论处理系统参数不确定性部分

本文将结合奇异摄动理论和切换控制理论对该类系统进行建模、系统稳定性分析和状态反馈控制器设计。借用文献［12］中对参数不确定部分的处理方法建立切换线性奇异摄动系统模型，利用谱范数、Lyapunov函数和线性矩阵不等式（LMIS）方法求解控制器增益，并结合实例验证该方法的有效性。本文以线性系统为例，未来研究可拓展到非线性奇异摄动系统。

1 非时延离散时间线性系统建模

根据被控系统采样速率的不同，离散时间奇异摄动系统可分为标准离散奇异摄动系统和非标准离散模糊奇异摄动模型，采用非时延标准离散奇异摄动系统模型如下

假设状态完全可测 ，状态反馈控制器

将控制律式（2）代入系统式（1）中，可得闭环系统模型

1.1 状态反馈控制器设计

1.1.1 矩阵谱范数法

定义1.1 设A为属于复矩阵空间 Cm×n的矩阵。按某一对应规则在 Cm×n上定义A的一个实值函数，记作。如果该函数满足如下条件：

其中，

那么存在 0*＞ε ，以至对于 ］，0（*εε∈∀ ，闭环系统式（3）渐进稳定。

鉴于εP的结构，可推出如果存在一个标量 ε，那么对于，矩阵εP满足如下等式

构造如下线性变换

由于

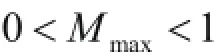
由于

切换规则选取：

首先是排比。“红砖墙/老牌楼/琉璃瓦”这句是三字偏正式词语的排比，短短九个字就勾勒出具有古典美、岁月感的时代环境，使得整首歌都染上了古意。

由式（6）得

令γ=1-Mmax，从式（9）可推出

对于式（12）应用Schur补定理可得

可将式（14）写为

1122

2 仿真实例

考虑一个四阶系统，离散时间切换奇异摄动系统模型

其中，

图1、图2分别为离散时间切换双时标系统的状态响应曲线和输出响应曲线，该仿真结果进一步验证了切换状态反馈控制器在处理奇异摄动参数不确定性系统时，该方法的有效性。

图1 闭环系统状态响应Fig.1 The state response of the closed-loop system

图2 闭环系统输出响应Fig.2 The output response of the closed-loop system

3 结论

本文融合切换理论和奇异摄动理论，对离散时间切换线性奇异摄动系统建模，切换理论的引入主要解决系统参数不确定性问题，参数不确定性部分是时变且有界的。利用矩阵谱范数法和线性矩阵不等式方法，研究了离散时间切换线性奇异摄动系统的模型建立和切换状态反馈控制器设计，将对控制器增益的求解转化为求解一组与摄动参数ε无关的线性矩阵不等式的问题，避免了由ε引起数值求解的病态问题，仿真结果表明证明了该方法的有效性。

参考文献

［1］ Robust stability of singularly perturbed state feedback systems using unified approach［J］.Control Theory and Applications， 2001， 148（5）：391-396.

［2］ Kyun-Sang Park， Hyun-Wook Jo， Jong-Tae Lim.Stability analysis of standard and non-standard nonlinear singularly perturbed system withuncertainty［C］.12thInternational Conference on Control， Automation and Systems.ICC， Jeju Island， Korea， 2012： 1833-1877.

［3］ Hongwang Yu， Baoshang Zhang.Stabilizability of a class of linear singularly perturbed systems via output feedback［C］.26th Chinese Control and Decision Conference， 2014： 4230-4233.

［4］ I.Malloci， J.Daafouz， C.Iung.Stabilization of continous-time singularly perturbed switched system［C］.In proceeding of the 48th IEEE Conference on Decision and Control and 28th Chinese Control Conference， Dhanghai， P.R.China， 2009： 6371-6376.

［5］ Tan， W.， T.Leung， Q.Tu."H control for singularly perturbated systems"［J］.Automatica， 1998， 34（2）： 255-260.

［6］ J.Chen， F.Sun， Y.Yin， C.Hu.State feedback robust stabi-lization for discrete-timefuzzy singularly perturbed systems withparameter uncertainty［J］.IET Control Theory Appl.， 2011， 5（10）： 1195-1202.

［7］ Yang Kun， Shen Yanxia， Ji Zhicheng.H∞memory state feedback control for uncertain nonlinear switched singular systems withtime-varying delay［C］.Proceedings of the 32nd Chinese Control Conference， Xian， China， July， 2013： 2073-2077.

［8］ M.Balde， U.Boscain， P.Mason.A note on stability c- onditions for planar switched systems［J］.Int.J.Control， 2009， 82（10）： 1882-1888.

［9］ I.Malloci， J.Daafouz， C.Iung.Stability and stabilization of two time scale switched systems in discrete time［J］.IEEE Transaction on Automatic Control， 2010， 55（6）： 1434-1438.

［10］ Fouad El Hachemi， Mario Sigalotti， Jamal Daafouz.Stability analysis of singularly perturbed switched linear sytems［J］.IEEE Transaction on Automatic Control， 2012， 57（8）： 2116-2121.

［11］ Ohtake.H，Tanaka.K，Wang.H.O.Switching fuzzy controller design based on switching Lyapunov function for a class of nonlinear systems［J］.Systems， Man， and Cybernetics， Part B： Cybernetics， IEEE Transactions on， 2006，36（1）： 13-23.

［12］ G-H.Yang， J-X.Dong.Switching Fuzzy Dynamic Output Feedback Control for Nonlinear Systems［J］.IEEE Trans.Syst.， Man， Cybern.B，Cybern.， 2010， 40（2）： 505-516.

［13］ G.Garcia， J.Daafouz， J.Bernussou. A LMI solution in the optimal problem for singularly perturbed systems［C］.Proceedings of the American Control Conferencen， Philadelphia， Pennsylvania， June， 1998： 550-554.

［14］ Fridman E.Effects of small of delays on stability of singularly perturbed systems［J］.Automatic， 38（5）， 897-902.

［15］ 冷永刚，田祥友.一阶线性系统随机共振在滑动轴承故障诊断中的应用研究［J］.新型工业化，2013，3（9）：92-98.Y G Leng， X Y Tian.One order linear stochastic resonance system in fault diagnosis of bearings on the application research ［J］.The Journal of New Industrialization， 2013， 3 （9）：92-98.

［16］ 邓夏， 贾庆轩， 褚明，等.基于动态切换函数的单杆柔性臂动态滑模——最优混合控制［J］.新型工业化，2012， 2（10）：59-66.X Deng， Q X Jia， M Zhu， et al.Dynamic sliding mode of single link flexible manipulator based on dynamic switching function： optimal hybrid control ［J］.The Journal of New Industrialization， 2012， 2 （10）：59-66.

DOI：10.19335/j.cnki.2095-6649.2016.06.002

基金项目：国家自然科学基金项目（51374082）

作者简介：陈旋（1990-），女，硕士，主要研究方向：复杂系统的建模和控制；陈金香（1972-）女，高级工程师，博士，主要研究方向：工业轧钢

Modeling and State Feedback Control of Discrete-time Singularly Perturbed Systems

CHEN Xuan， CHEN Jin-xiang
（Inner Mongolia University of Technology ， College of electric power， Huhehaote ， Inner 010080， China ）

ABSTRACT：For a class of discrete-time singularly perturbed complex system with uncertain part， combining the singular perturbation theory with the switching theory， a dynamic model of switched discrete-time singularly perturbed systemsis builted.Switching mechanism is introduced to handle the unknown parameters， to achieve the precise control performance of the system.Stability a analysis and state-feedbackcontrol problems for switched discrete-time singularly perturbed systems （DSTTSs） are mainly investigated in this paper.With the spectral matrix normand linear matrix inequalities （LMIs） approaches ， a series problems are solved by a set of ε-independent linear matrix inequalities.A numerical example is presented to illustrate the effectiveness of the proposed approach.

KEyWORDS：Discrete-timesingularly perturbed system； Parameter uncertainties； Switching control； State feedback； Linear matrix inequalitiees （LMIs）