诱导孔对铝合金薄壁梁轴向压缩变形行为的影响

王　冠，刘志文，徐从昌，李落星（1.宁夏大学 机械工程学院，银川 75001；.湖南大学 汽车车身先进设计制造国家重点实验室，长沙 41008）

诱导孔对铝合金薄壁梁轴向压缩变形行为的影响

王冠1，2，刘志文2，徐从昌2，李落星2
（1.宁夏大学 机械工程学院，银川 750021；2.湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082）

以6063铝合金薄壁梁结构为研究对象，采用准静态轴向加载的方式，借助WAW-E600型微控万能试验机，探明诱导孔结构对铝合金薄壁梁压缩变形行为与吸能性能的影响规律。研究表明：单排诱导孔能够使试样的变形模式由欧拉模式转变为混合模式，提高试样变形的稳定性，降低载荷峰值，吸能性能增加26.78%。多排诱导孔的位置与尺寸对薄壁梁的变形有较大影响，试样中部的诱导孔会降低结构稳定性，使试样失稳以欧拉模式变形为主，其载荷水平及吸能性能均较低；尺寸呈梯度变化的诱导孔能够使试样发生手风琴模式的变形，试样顺序压溃，载荷波动平稳，吸能性能较高；大尺寸诱导孔会使试样在局部发生剪切变形并逐层顺序压溃，其载荷平稳，是一种新的变形模式。通过实验数据对比，系统研究诱导孔尺寸对临界载荷的影响规律，并基于线形回归理论，建立铝合金薄壁梁结构临界载荷与截面惯性矩之间的定量关系。

薄壁梁；诱导孔；准静态压缩；压溃行为；变形模式

在汽车工业中，薄壁梁是组成汽车车身结构的重要零部件，在车身安全结构中有着广泛的应用［1］。薄壁梁结构的压溃变形行为是车身设计中的关键，其载荷峰值不能超过后端结构的承载极限［2］。增加诱导结构有助于降低薄壁梁峰值载荷，改善压缩性能。在过去的几十年中，很多学者对薄壁梁的诱导结构及其变形行为进行了深入的研究［3-6］。ZHANG等［7-8］研究了预变形对多胞截面薄壁梁以及单胞方管填充结构压缩性能的影响，发现预变形凹槽不仅能有效降低吸能盒在压缩过程中的峰值载荷，而且还能有效提高材料的利用率。KORMI等［9］通过数值仿真，研究了3种不同工况下开设诱导孔时钢管的变形行为，并对每一种工况做了细致的分析。SAHU等［10-11］与KREMER等［12］研究了诱导孔对复合材料变形行为的影响，指出诱导孔直径，边界条件等对试样的变形模式有较大的影响。KRAUSS等［13］研究了多种不同形状诱导结构对薄壁梁动态冲击载荷的影响，结果表明增加诱导结构能够使试样的峰值载荷降低约44%。LEE等［14］发现，诱导孔不仅会对试样局部产生弱化效果，而且会影响结构的稳定性，使试样以完美的对称模式压缩变形。

铝合金具有比钢更高的比吸能性及变形稳定性，是汽车轻量化的理想材料［15］。铝合金薄壁梁结构的轴向压缩变形行为对汽车的安全性具有重要影响［16］，关于诱导结构对铝合金薄壁梁变形行为影响的受到了国内外学者们的广泛关注。LEE等［17］研究了碳纤维包覆形式对铝合金薄壁梁压缩变形的诱导作用，结果表明采用90°/0°的纤维缠绕方式能够获得最优的吸能性能。向东等［18］系统研究了时效状态对单排诱导孔的多胞铝合金薄壁梁结构变形模式及承载能力的影响。ARNOLD等［19-20］借助试验与仿真手段研究了诱导孔直径对T4及T6态6061铝合金薄壁梁压缩性能的影响，结果表明，铝合金薄壁梁的吸能性能主要取决于材料的力学性能，引入诱导孔能提高薄壁梁的吸能性能和名义载荷水平，但是影响较小。GHAZIJAHANI等［21］通过不同尺寸、热处理状态的铝合金、中碳钢材质圆管轴向压缩变形实验，研究了试样中部不同诱导孔直径、位置、数量对圆管压缩变形行为的影响，并讨论了典型变形模式与载荷曲线之间的关系，结果表明，诱导孔对于薄壁梁的压溃模式有重要影响，即使是长径比很大的圆管也有可能避免欧拉模式的压溃变形。CHENG等［22］针对试样中部的诱导孔，探索了诱导孔形状及尺寸对铝合金方管失效变形行为的影响。HAN等［23］研究了冲击载荷下方形诱导孔尺寸、位置对铝合金圆管承载能力及吸能性能的影响，并建立了数学模型。

综上所述，目前国内外关于铝合金薄壁梁诱导结构的相关研究并不完善，文献中缺少关于多排诱导孔的位置、排布及尺寸变化对薄壁梁压缩变形行为影响的研究，特别是大尺寸诱导孔对薄壁梁变形模式的影响无相关报道。本文作者以6063铝合金多胞截面薄壁梁试样作为研究对象，系统分析了薄壁梁结构在不同诱导孔影响下的准静态压缩行为与吸能性能，为汽车车身吸能结构设计提供参考。

1　实验

1.1实验材料

本试验中采用半连续铸造加工的6063铝合金，表1所列为6063铝合金各元素质量分数实测值。

1.2实验方法

实验所采用的型材使用XJ-2500型挤压机加工，挤压过程中型材温度控制在450～500℃，并在出模口位置在线水淬。图1所示为铝合金多胞薄壁型材的尺寸图，由图1可知挤压型材截面由内外两个八边形组成，内外层八边形轴向转角为22.5°，内外两层八边形由4条加强筋相连。试样沿挤压方向截取长度为200 mm，并通过切削的方式保证两端的平行度。将试样在DHG型干燥箱中180℃热处理30 min。铝合金薄壁梁试样的准静态轴向压缩试验在WAW-E600型微控电液伺服万能试验机上进行，并由计算机实时记录载荷变化，试验压缩速度为5 mm/min，使用照相机实时记录薄壁梁结构在典型载荷状态下（载荷曲线的峰值、谷值等）的变形情况。由于铝合金薄壁梁变形稳定，可重复性高，每种类型试样做3组试验。

表1　6063铝合金各元素化学成份Table 1　Chemical composition of 6063 aluminum alloy （mass fraction，%）

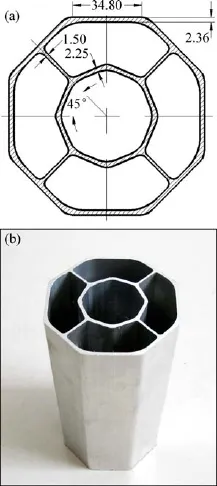
图1　6063合金型材的几何形状与尺寸Fig.1　Dimensions and geometric shape of 6063 aluminum profile　（unit：mm）：（a）Cross-section　dimensions；（b）Practicality diagram

2　结果与分析

2.1无诱导孔薄壁梁

图2所示为无诱导孔试样（Base试样）轴向压缩试验的典型载荷-位移曲线。由图2可知，铝合金薄壁梁以欧拉模式变形。从加载开始到A点，试样均处于弹性屈曲变形阶段，表面出现均匀的起伏，载荷迅速增加。随着压缩量的继续增大，试样进入塑性屈曲变形阶段，局部出现失稳，发生压溃变形。试样中部一组面向外凸起变形，而垂直方向上两个面向内凹陷，形成第一个塑性铰。试样在B点处载荷达到峰值FP（228.89 kN）。之后，载荷下降至最低点C（101.76 kN），形成一个完整的褶皱。试样上下两端的未变形区相互接触，开始变形，载荷波动上升。当变形至D点，薄壁梁试样被完全压缩。D点后为致密化过程，试样的有效压缩长度δ=133.68 mm。

在该变形模式下，铝合金薄壁梁结构中部首先发生失稳，试样仅形成一个褶皱，载荷曲线呈现出一个明显的波峰与波谷，因此无法充分发挥结构的吸能性能，是一种不理想的变形模式。

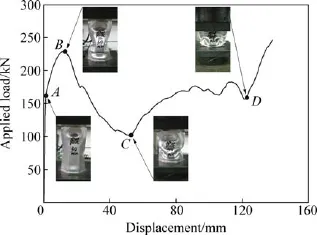
图2　Base试样的变形行为Fig.2　Compression behavior of Base sample

2.2单排诱导孔薄壁梁

根据半波长理论或借助有限元仿真等手段，可以准确计算诱导孔的合理位置［2］。在铝合金薄壁梁试样无加强筋的4个外表面上，距离试样顶端13.5 mm位置开设直径10 mm的诱导孔，并贯穿内八边形，试样编号为One-hole，如图3所示。

图4所示为单排诱导孔试样轴向压缩变形载荷-位移曲线。由图4可知，引入诱导孔后试样的变形模式发生了改变，具有更好的规律性。在试样变形初期，即从初始加载至A阶段为均匀的弹性屈曲阶段至B点处（204.02 kN）载荷达到峰值，由于诱导孔的局部弱化效应，在开孔处发生失稳变形，外层八边形结构向外反转，试样上端诱导孔一周拱起，形成第一个塑性铰，越过峰值后，试样的承载能力迅速下降至C点（126 kN），此时，形成了第一个完整的褶皱。并随着变形量的增加，呈现出自上而下的顺序压溃。试样One-hole完成2个完整的褶皱后，变形模式由手风琴模式转变为金刚石模式，变形规律性被打破。对比图4和图2可知，开设诱导孔后，试样压缩变形稳定，载荷波动平稳，试样有效压缩长度为145.27 mm，较Base试样的增加9%。因此，合理的诱导孔有助于提高薄壁梁的变形稳定性与吸能性能。

试样One-hole在第二个褶皱形成时，由于没有诱导孔的弱化效应，因此第二载荷峰值为216.30 kN，略高于第一载荷峰值。在汽车结构安全设计中，薄壁梁结构的载荷峰值通常会有上限约束，不能超过后端结构的承载极限，否则会引起其它部件的破坏。在薄壁梁结构上合理开设诱导孔，能够使载荷峰值降低10.5%（5%），有助于薄壁梁吸能性能的充分利用。

图3　开孔后试样的实物图Fig.3　Aluminum profile with cut-outs

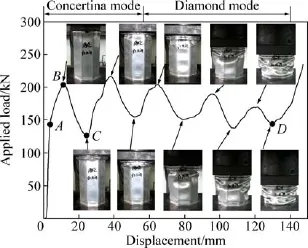
图4　单排诱导孔试样One-hole的变形行为Fig.4　Compression behavior of sample One-hole

2.3多排诱导孔薄壁梁

2.3.1诱导孔位置的影响

诱导孔开设的位置对于试样的压缩变形行为有较大影响，合理的开孔位置能够起到诱导变形的作用，反之将破坏试样原有的变形模式。为研究诱导孔位置对薄壁梁结构压缩变形模式及载荷水平的影响，进行3组对比试验，诱导孔直径均为10 mm，但位置不同。编号为试样Multi-holes-01，在距离试样顶部13.5 mm开设诱导孔，后每隔72 mm开2个诱导孔；试样Multi-holes-02，距试样顶部13.5 mm开设诱导孔，后每隔36 mm开2个诱导孔；试样Multi-holes-03，距试样顶部13.5 mm开设诱导孔，后每隔36 mm共开4个诱导孔。所有诱导孔位于试样外八边形无加强筋的4个表面上，并贯穿内八边形结构，如图5所示。

图6所示为3组试样的典型压缩变形结果。由图6可知，由于诱导孔的弱化效应，在加载过程中应力容易在试样中间位置集中，3组试验均在靠近试样中部的诱导孔附近首先发生失稳，试样的变形模式为欧拉模式。其中，试样Multi-holes-02中3个诱导孔均分布在上端且距离较近，使得试样上半部分结构稳定性发生变化，但对下半部分没有明显的影响，因此试样在压缩过程中呈现出两个不同的变形阶段，加载初期试样中部首先发生失稳，并随着压缩量的增加试样上部发生欧拉模式变形，压缩完全后，试样下部继续以金刚石模式变形，其变形过程相对其他两组试样的更规律一些。

图5　多排诱导孔试样开孔位置示意图Fig.5　Location of multi-row cut-outs on the samples：（a）Multi-holes-01；（b）Multi-holes-02；（c）Multi-holes-03

图6　多排诱导孔试样压缩变形结果Fig.6　Compression result of multi-row cut-outs samples：（a）Multi-holes-01；（b）Multi-holes-02；（c）Multi-holes-03

图7所示为3组试样在准静态压缩过程中的典型载荷-位移曲线。由图7（a）可知，3组方案在第一峰值前，载荷相近，但由于诱导孔位置及数量的不同使试样在屈曲阶段的应力分布状态出现差异，3组试样第一峰值有较小的变化。随着变形量的增加，3组试样均在中部发生失稳变形，并在波谷处形成一个完整的褶皱。随后的3组试样的变形模式出现差别，其中试样Multi-holes-02以金刚石模式变形，其载荷水平最高，其他试验继续以欧拉模式变形。试样Multi-holes-03由于开设诱导孔数量较多，载荷水平最低。由图7（b）可知，3种方案最终压溃变形量δ相近，约为135 mm，均小于以混合模式变形的单排诱导孔薄壁梁试样（145.27 mm）。图7（c）表明，由于变形模式的差异3种试样的吸能性能不同，其中Multi-holes-02在后期发生钻石模式的压缩变形，能够吸收更多的能量。

由试验结果可知，开设诱导孔的位置对于薄壁梁结构的变形模式有较大的影响，诱导孔分布间隔过大将对薄壁梁结构产生不利的影响，尤其是在薄壁梁中部的诱导孔，会使变形过早的在试样中部集中，试样更容易发生欧拉模式的失稳变形。而欧拉模式与其他变形模式相比，薄壁梁结构可压缩距离减小，载荷波动明显且名义载荷水平较低，不能在变形过程中充分发挥吸能性能，其变形吸能较少。因此，应尽可能地将诱导孔分布在薄壁梁端部，并避免在梁结构最容易发生应力集中及失稳的位置开设诱导孔。

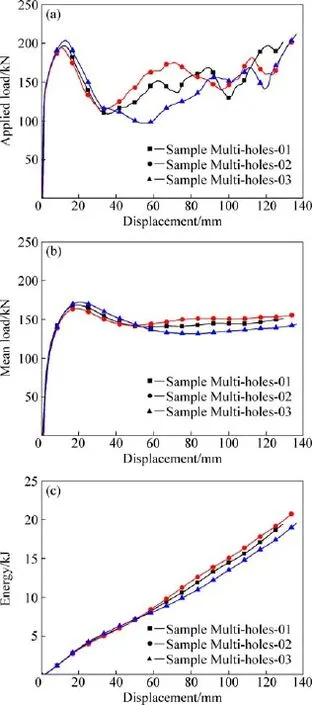
图7　多排诱导孔试样的加载载荷、平均载荷以及吸能性能的变化Fig.7　Curves of applied load，mean load and energy versus displacement of samples with multi-row cut-outs：（a）Applied load；（b）Mean load；（c）Absorbed energy

2.3.2诱导孔尺寸的影响

诱导孔的局部弱化效应对薄壁梁结构的轴向压缩变形具有较大的影响，但由于将孔开在试样中部会诱导其首先在中部发生失稳变形，此变形模式不利于能量的吸收以及变形的稳定性，因此需要通过调整开孔方案，使试样发生更加稳定的压溃变形。诱导孔直径的变化会对结构产生不同的弱化效果。通过梯度变化诱导孔直径，逐级弱化结构强度，以实现薄壁梁的顺序压缩变形。进行以下两组实验，试样开孔位置如图8所示。试样Multi-holes-04在距顶部13.5 mm位置开设直径为d15.5 mm的诱导孔，后每隔36 mm开4个d12 mm的诱导孔；试样Multi-holes-05在距顶部13.5 mm处开设d15.5 mm的诱导孔，后每隔36 mm开3排直径分别为d14 mm、d12 mm、d10 mm的诱导孔。

图8　多排诱导孔试样开孔位置示意图Fig.8　Location of multi-row cut-outs on samples：（a）Sample Multi-holes-04；（b）Sample Multi-holes-05

通过与前组试验结果对比可知，在加载初期，等径均布诱导孔试样Multi-holes-03与梯度变化诱导孔尺寸的试样Multi-holes-04和Multi-holes-05均未发生局部失稳，应力集中在结构强度较弱的诱导孔位置，形成规律上下起伏的褶皱，试样表面均出现了明显的波动，如图9所示。由图9可知，由于试样Multi-holes-03 5个诱导孔大小相等且均匀分布，变形初期应力在各个孔位置大小相同，试样表面呈现均匀的褶皱。试样Multi-holes-04第一个诱导孔直径大于其他孔的，因而该位置结构强度低于其他位置的，更容易发生应力集中，根据图9可以看出，试样应力集中区趋势自上而下逐渐减少，至第5排孔已无明显的褶皱。试样Multi-holes-05孔直径从上至下顺序减小，结构弱化的影响也依次减弱，因此应力在上端集中最为明显，变形较大，而下端应力集中较小，无明显褶皱。通过对比可知，变化诱导孔直径，对于试样压缩初期有较大的影响，在诱导孔直径较大位置附近，由于局部弱化效应明显，应力更容易集中，薄壁梁会在此处首先发生变形。试验结果表明，试样Multi-holes-03失稳首先发生在试样中部，而试样Multi-holes-04、Multi-holes-05变形首先发生在第1排诱导孔的位置，并以手风琴模式自上而下顺序压缩变形。

图10所示为试样Multi-holes-03、04、05的变形结果。由图10可知，试样Multi-holes-04由于具有更多的诱导孔，其变形模式比试样Multi-holes-05的更稳定，压缩变形后形成了6个完整的褶皱，而试样Multi-holes-05在形成4个完整褶皱后，变形出现不稳定，发生金刚石模式变形。

图11所示为梯度变化诱导孔试样Multi-holes-04的变形过程及位移-载荷曲线，由图11可知，试样的变形模式为手风琴模式，第一个褶皱的形成过程与单排诱导孔试样One-hole相同，试样在B点处载荷达到峰值（198.63 kN），诱导孔位置发生失稳，形成第一个塑性铰，越过峰值后，试样的承载能力迅速下降至C点（125.41 kN），此时，形成了第一个完整的褶皱。之后的变形重复上述过程，载荷-位移曲线呈现周期性的波峰与波谷。至D点时，试样被完全压缩，试样自上而下依次形成6个褶皱，图中每一个波谷对应着一个完整褶皱的形成，而每一个波峰对应着一个塑性铰的形成。试样 Multi-holes-05变形过程与试样Multi-holes-04的相似。

图9　多排诱导孔试样轴向压缩初始阶段变形结果Fig.9　Compression results of multi-row cut-outs samples at initial　state：（a） Sample　Multi-holes-03；（b） Sample Multi-holes-04；（c）Sample Multi-holes-05

图10　多排诱导孔试样压缩变形结果Fig.10　Compression results of multi-row cut-outs samples：（a）Sample Multi-holes-03；（b）Sample Multi-holes-04；（c）Sample Multi-holes-05

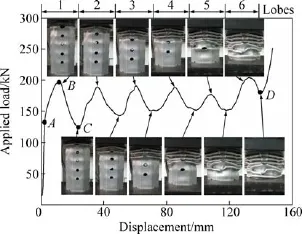
图11　多排诱导孔试样Multi-holes-04的变形行为Fig.11　Compression behavior of sample Multi-holes-04

图12所示为试样Multi-holes-04、Multi-holes-05在准静态压缩过程中的载荷-位移曲线，由图12（a）可知在第一峰值前，两组方案载荷相近，但由于诱导孔直径变化规律不同导致峰值出现差别，两组试样第一排孔直径均为15.5 mm，但试样Multi-holes-04的第二排孔直径为12 mm，试样Multi-holes-05为14 mm，因此后者在第二个褶皱形成处结构强度较低，导致试样Multi-holes-05的第一峰值低于试样Multi-holes-04的。当第4个褶皱形成后，由于试样Multi-holes-05没有诱导孔的弱化影响，其载荷超过试样Multi-holes-04的，变形模式发生改变。由图12（b）和（c）可知，两组试样的名义载荷与吸能性能差异较大，与诱导孔尺寸和数量的不同有重要关系。由试验结果可知，顺序减小诱导孔的直径可以使薄壁梁结构发生从上至下的顺序压溃变形，且峰值间距相等，变形稳定性较好。第一、二排诱导孔直径的变化对于薄壁梁结构变形模式的影响最大，合理调整一、二排孔径，形成一个完整的褶皱后试样就能保持稳定的模式发生顺序变形。

综上所述，诱导孔直径的变化对于薄壁梁结构的变形模式具有较大的影响，通过合理设计孔径的变化，能够充分诱导试样按照一定的顺序变形，且变形模式稳定。当试样一端诱导孔直径大于其他位置时的，该诱导孔位置首先发生失稳变形，且初始阶段的变形模式为手风琴模式。同时，诱导孔开设的数量对变形模式也有较大的影响，根据薄壁梁的半波长合理开设诱导孔，其分布数量越多，试样变形模式越稳定。但数量过多的诱导孔会降低薄壁梁结构的承载能力，影响其吸能性能。

2.3.3大尺寸诱导孔的影响

当诱导孔的直径继续增大，其弱化效应会影响截面的承载能力。在铝合金薄壁梁试样上开设诱导孔，如图13所示，试样编号为Multi-holes-06，在距试样顶部13.5 mm开d15.5 mm的诱导孔后，每隔36 mm依次开设4排诱导孔，孔径分别为d15 mm、d14.5 mm、d14 mm、d13.5 mm。

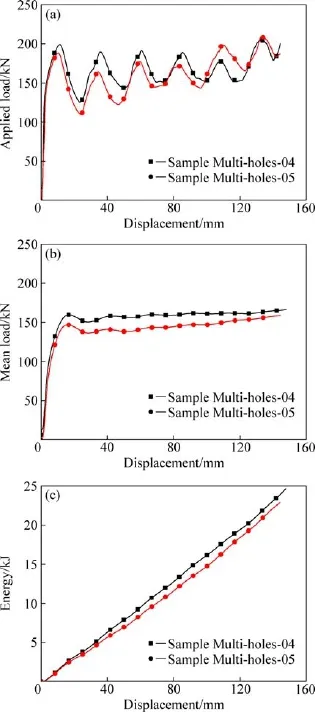
图12　多排诱导孔试样的加载载荷、平均载荷以及吸能性能的变化Fig.12　Curves of applied load，mean load and energy versuse displacement of samples with multi-row cut-outs：（a）Applied load；（b）Mean load；（c）Absorbed energy

图14所示为大尺寸诱导孔薄壁梁试样轴向压缩变形载荷-位移曲线，由图14可知，加载开始至A阶段载荷迅速增长，试样处于均匀的弹性屈曲阶段，当载荷增大到一定程度后，由于诱导孔直径较大，试样局部抗弯曲能力较低，第一、二排诱导孔同时发生变形，形成塑性铰；随后，载荷增加的速度减慢，弹性屈曲逐渐转化为塑性屈曲，并最终在B点处（192.81 kN）达到峰值。由于诱导孔的结构弱化作用明显，试样的棱边首先发生失稳，并向诱导孔的一侧倾转。随着压缩量的增加，诱导孔两侧45°位置发生扭转，塑性铰上下等距的金属开始弯曲变形，诱导孔左侧上方的金属凸起变形，左下侧内凹，形成一个褶皱，同时诱导孔右侧上方内凹，右下方凸起，形成一个与之对称的褶皱；当载荷越过峰值后，试样的承载能力迅速下降至C点（126.73 kN）。此时，在第二排孔沿45°方向与第一、三排孔之间形成了第一个完整的褶皱。之后的载荷-位移重复上述过程，呈现较为周期性的波峰与波谷。由于诱导孔直径不断减小，载荷峰值随变形量增加不断增大。至D点时，试样被完全压缩，D点以后为致密化过程。由于每两个孔之间的棱边在压缩过程中未发生明显变形，因此试样整体压溃距离较短。

图13　大尺寸诱导孔试样Multi-holes-06开孔位置Fig.13　Locationoflargesizecut-outson sampleMulti-holes-06

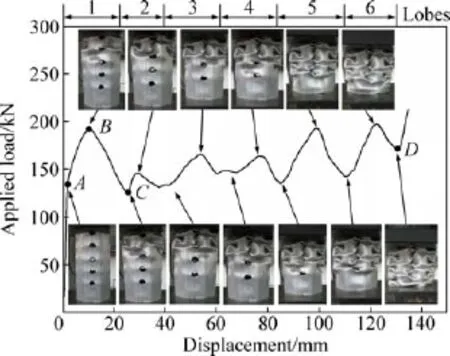
图14　大尺寸诱导孔试样Multi-holes-06的变形行为Fig.14　Compression behavior of sample Multi-holes-06 with large size cut-outs

根据实验结果可知，过大的诱导孔直径会使薄壁梁结构的变形模式发生明显转变。当诱导孔直径增大到一定程度，对结构的弱化效应明显，试样的截面由外延变形转变为切向的扭转变形。图14所示的变形模式在前人的研究工作中均未有过相关报道，是一种新的薄壁梁结构变形模式，暂称为New模式。与其他变形模式相比，该变形模式第一峰值载荷较低，平均载荷的波动更小，变形更稳定，但由于试样的有效压缩距离小于手风琴模式，因此吸能性能相对较低。

3　分析与讨论

3.1临界失稳载荷

为了探明诱导孔尺寸对铝合金薄壁梁结构临界失稳载荷的影响，选取一组典型诱导结构的载荷-位移曲线，截取第一峰值前的部分作为研究对象。由图15可知，在达到峰值前，载荷曲线可以分为3个阶段：呈线形增长的弹性变形阶段，失稳阶段，失稳后的塑性变形阶段。由于诱导孔尺寸、分布位置的差异，不同铝合金薄壁梁结构的载荷曲线存在明显的区别。随着诱导孔尺寸的增大，试样弹性加载阶段的斜率以及峰值载荷逐渐降低。其中无诱导孔Base试样弹性段 斜率最高，承载能力明显优于开设诱导孔试样，说明诱导孔对于结构的承载具有非常大的影响，通过合理设计诱导结构能够灵活调整薄壁梁的承载性能。试样发生失稳以后，载荷增速减慢但仍继续增大，此阶段中，不同尺寸诱导孔试样载荷的增加速度相近。当载荷增大至第一峰值后，开始出现下降。

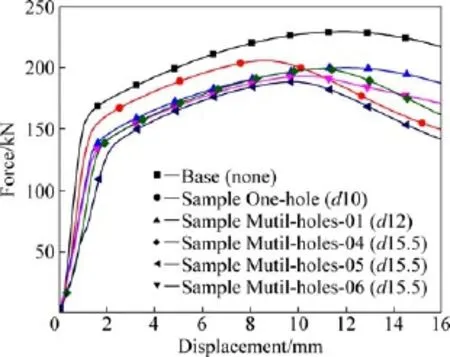
图15　第一峰值前试样的载荷-位移曲线Fig.15　Force-displacement curve of samples before 1st peak

为准确获得铝合金薄壁梁结构发生失稳时的临界载荷，对试样的载荷-位移曲线进行微分，并结合LangevinMod非线性拟合，获得载荷的变化率曲线，如图16所示。由图16可知，曲线由3个典型阶段组成，在压缩变形初期，无诱导孔试样斜率最大，在变形约为0.7 mm时，载荷曲线的斜率开始降低，当压缩变形至约1.5 mm时，斜率变化减慢并趋于稳定。通过对比可知，在弹性加载阶段，随着诱导孔尺寸的增加，载荷曲线的斜率逐渐降低，斜率下降点后延；在失稳阶段，有诱导孔试样斜率的变化率较无诱导孔试样明显降低；随着压缩变形量的增大，所有试样的载荷变化率在发生失稳后均趋于一致。其中试样Multi-holes-05弹性阶段的压缩变形量约为1.5 mm，是无诱导孔试样的2倍，随后试样的载荷变化率逐渐降低，但整体变化平缓，并在压缩变形量为3.0 mm时达到稳定。说明诱导孔不但会改变试样的压缩变形模式，同时也会对试样的加载过程产生影响。随着诱导孔尺寸的增加，弹性变形阶段与塑性变形阶段之间的过渡更加光滑，试样由于结构失稳产生的载荷波动越来越不明显。

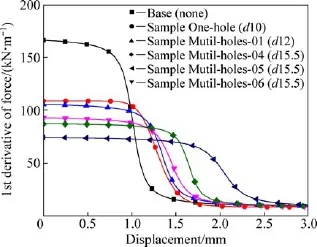
图16　试样的载荷-位移曲线的1阶导数Fig.16　1st derivative of force-displacement curve

对图16再次进行微分求导，能够获得试样载荷斜率的变化率曲线，如图17所示。曲线的最低点对应结构承载能力的突变，即为发生失稳的临界变形量Dcr。由图17可知，无诱导孔试样在压缩量为1.0 mm时最先发生失稳，而大尺寸诱导孔（d15.5 mm）试样发生失稳对应的压缩变形量较大。根据图17得到结构失稳时的临界变形量Dcr，结合图15能够准确获得铝合金薄壁梁结构的压缩失稳临界载荷Fcr。

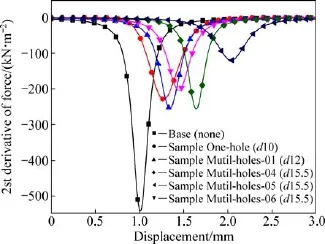
图17　试样的载荷-位移曲线的2阶导数Fig.17　2nd derivative of force-displacement curve

表2所列为不同诱导孔尺寸的试样在发生临界失稳状态下的实验数据，由表2可知，铝合金薄壁梁结构的截面惯性矩（I）与诱导孔的尺寸直接相关。随着试样截面惯性矩的减小，其压缩失稳的临界载荷Fcr不断降低，而临界压缩变形量Dcr有所增加。当诱导孔的直径一定（d15.5 mm），尽管试样变形模式存在差异，试样的惯性矩与临界失稳载荷仍将保持稳定。因此，可以通过建立惯性矩与临界载荷的定量关系来描述和预测结构的承载能力。

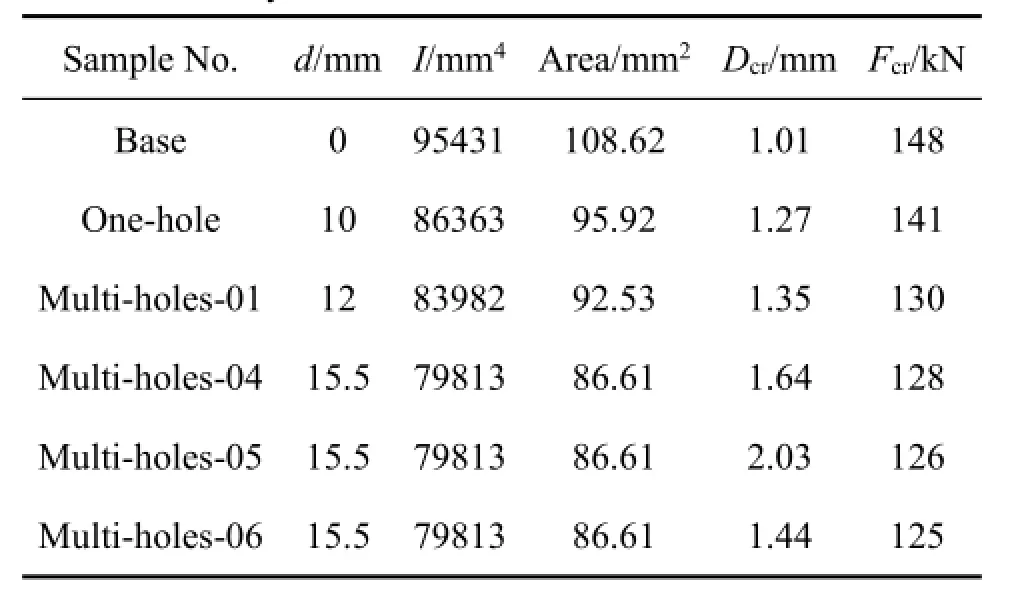
表2　铝合金薄壁梁临界失稳状态的实验数据Table 2　Experimental data of thin-walled aluminum profile at critical instability state

将表2中的数据进行整理，根据线性拟合可以获得惯性矩与临界载荷之间的关系，如图18所示。拟合结果得到相关性系数R2为0.90，说明该线形拟合关系具有良好的精度，能够用于同类数据的描述与分析。因此，铝合金薄壁梁结构压缩变形的临界载荷与截面惯性矩之间的关系可用公式表示为：

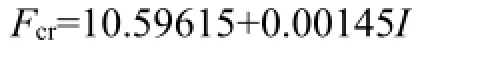
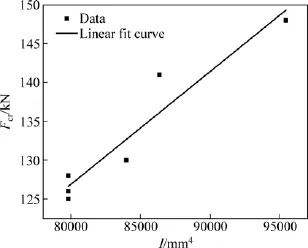
图18　惯性矩与临界载荷的线形拟合Fig.18　Linear fitting of inertia and critical force

3.2变形模式与载荷水平

针对铝合金薄壁梁结构完整的压缩变形过程，对比分析不同诱导孔影响下典型试样的变形模式及载荷水平，如表3所列。其中，γ为名义载荷与峰值载荷的比；E为总变形能；η为单位压溃距离的变形能。除样品Multi-holes-06外，试样在诱导孔的影响下，平均载荷Fm与无诱导孔Base试样的相比，均有不同程度的提高，最大增幅约为11.5%。

对比分析表3数据可知，引入诱导孔能够降低薄壁梁在压缩过程中的峰值载荷，试样Base在开诱导孔后其峰值载荷降低约10.5%。随着诱导孔的引入，试样的变形模式发生改变，其平均峰值载荷比γ与未开设诱导孔试样相比有明显提高，使试样能够更加充分的发挥自身的吸能性能。虽然未开设诱导孔时，薄壁梁试样吸能较低（19475.66 J），但是其可压缩距离较小（133.68 mm），因此平均吸能性能仅略小于开设诱导孔的试样。

从图19（a）可以看出，无诱导孔试样的变形模式为欧拉模式，变形首先发生在试样中部，第一峰值载荷较高，共出现2个峰值，曲线波动性较大；开设单排诱导孔后由于变形模式转变为混合模式，其载荷-位移曲线呈规律性波动，共出现5个峰值，各峰值间距相近，压缩变形前期峰值波动较大，后期载荷波动逐渐降低；通过改变一、二排诱导孔的直径可以顺序诱导试样变形，其变形模式为手风琴模式。由于第一、二排孔直径较大，因此峰值载荷略低于单排诱导孔试样，但压缩变形过程中试样变形稳定，载荷-位移曲线波动平稳；大尺寸诱导孔的试样以一种新的模式发生变形，峰值载荷最低，在压缩变形过程中，发生顺序压溃，共出现6个峰值，各峰值间距有小的波动，由于诱导孔尺寸的变化，第一峰值后载荷波动突然减小，随后波动性逐渐增大。

由图19（b）和（c）可知，4种变形模式中，欧拉模式的第一峰值最高，峰值持续时间较长，其名义载荷波动最大，其他3种变形模式的第一峰值相近，名义载荷变化平缓，变形过程更加稳定。在变形稳定阶段，混合模式的名义载荷水平较高，欧拉模式与New模式的名义载荷相近，手风琴模式名义载荷水平居中，该现象与诱导孔对薄壁梁结构承载能力的弱化作用有关。因此，欧拉模式在试样变形前期吸能性能最高，随后增速逐渐降低。混合模式吸能性能与手风琴模式的相近，随着变形量的增大，吸能性能迅速提高。New模式在变形过程中吸能性能变化稳定，呈线性增长趋势。

综上所述，开设诱导孔后铝合金薄壁梁结构的变形模式转变为混合模式或手风琴模式，使试样的压溃距离增加，与未开设诱导孔试样相比，薄壁梁在压缩过程中所吸收的能量E有所提高。试验结果表明，薄壁梁结构在压缩过程中以欧拉模式或金刚石模式变形时，合理引入诱导孔能有效提高薄壁梁结构的吸能性能与变形稳定性，但诱导孔过大时会使薄壁梁结构的变形转变为一种新的模式，该变形模式下试样压缩不充分，吸能性能降低。诱导孔尺寸对试样的临界载荷有直接影响，基于线形回归理论能够建立铝合金薄壁梁结构临界载荷与截面惯性矩之间的定量关系。

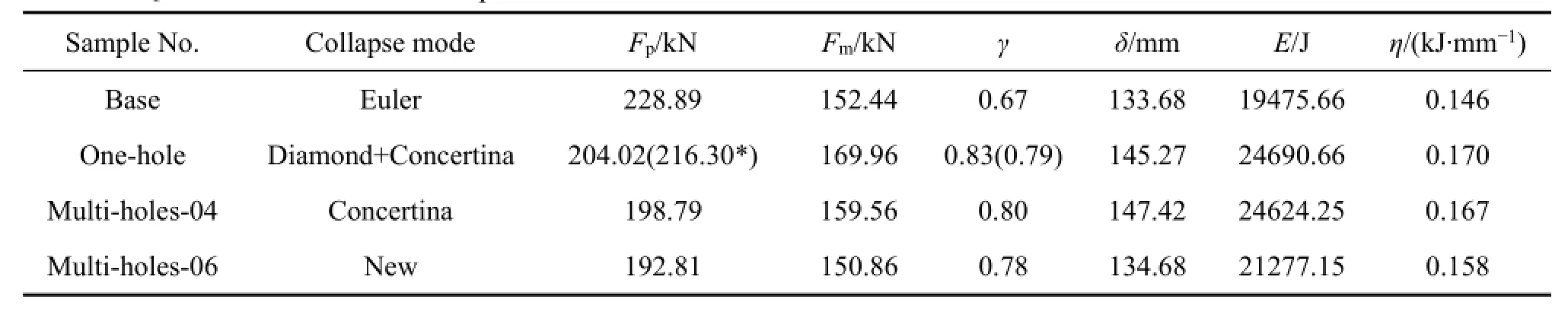
表3　铝合金薄壁梁开诱导孔前、后的压缩试验结果Table 3　Quasistatic test results of samples for various cut-outs

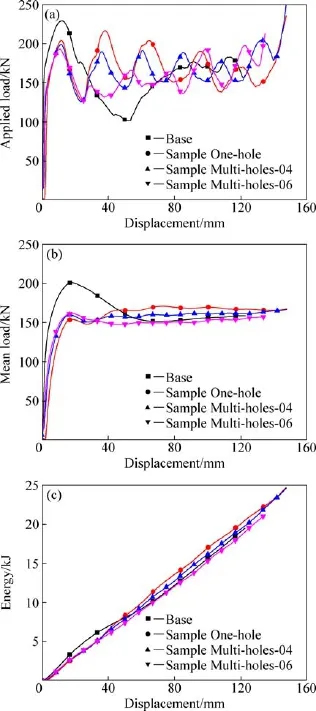
图19　试样在不同诱导条件下的加载载荷、平均载荷以及吸能性能的变化Fig.19　Curves of applied load，mean load and energy versus displacement of samples with different cut-outs：（a）Applied load；（b）Mean load；（c）Absorbed energy

4　结论

1）合理设计单排诱导孔能够使薄壁梁试样的压缩变形由欧拉模式转化为混合模式，提高试样压缩变形的稳定性，降低第一峰值载荷，增大变形载荷均值与吸能性能。

2）多排诱导孔的位置与尺寸对薄壁梁结构压缩变形模式有较大影响，诱导孔开设在试样中部，容易使试样中部首先发生失稳并以欧拉模式变形，梯度变化诱导孔直径能够使试样发生稳定的顺序变形，其压缩变形模式为手风琴模式。

3）诱导孔直径过大时，其45°对角线位置发生剪切变形，薄壁梁试样的压缩变形模式为一种全新的类型。在该变形模式下，试样载荷波动较小，但由于可压溃距离减少，薄壁梁结构的吸能性能降低。

4）铝合金薄壁梁结构压缩变形的临界载荷与截面惯性矩呈线性相关，随着诱导孔尺寸的增加，失稳阶段载荷的变化率逐渐减小。

REFERENCES

［1］ 张金换，杜汇良，马春生.汽车碰撞安全性设计［M］.北京：清华大学出版社，2010：190-204. ZHANG Jin-huan，DU Hui-liang，MA Chun-sheng.Automotive design for crash safety［M］.Beijing：Tsinghua University Press，2010：190-204.

［2］杜星文，宋宏伟.圆柱壳冲击动力学及耐撞性设计［M］.北京：科学出版社，2004：38-65. DUXing-wen，SONGHong-wei.Impactdynamicsand crashworthiness design of cylindrical shell［M］.Beijing：Science Press，2004：38-65.

［3］ 王鹏翔，徐立伟，张亮，高勇丽，吴沈荣.薄壁直梁件碰撞诱导变形模拟分析［J］.汽车工程，2008，30（11）：990-992. WANG Peng-xiang，XU Li-wei，ZHANG Liang，GAO Yong-li，WU Shen-rong.A simulation analysis on induced deformation in the impact of thin walled column［J］.Automotive Engineering，2008，30（11）：990-992.

［4］ 吴晓杰，胡宏勋，刘学军，崔振山.薄壁梁轴向压溃力的影响参数［J］.机械设计与研究，2012，28（1）：1006-2343. WU Xiao-jie，HU Hong-xun，LIU Xue-jun，CUI Zhen-shan. Study of design parameters influencing the axial folding force of thin-walled columns based on VCS models［J］.Machine Design and Research，2012，28（1）：1006-2343.

［5］ 武和全，胡宏伟，辛勇.薄壁梁诱导槽结构抗撞性优化设计及应用［J］.公路交通科技，2011，28（1）：120-126. WU He-quan，HU Hong-wei，XIN Yong.Optimal design of thin-walled rail with inducing groove for crashworthiness and its application［J］.Journal of Highway And Transportation Research and Development，2011，28（1）：120-126.

［6］ XIE S C，ZHOU H，ZHAO J J，ZHANG Y C.Energy-absorption forecast of thin-walled structure by GA-BP hybrid algorithm［J］. Journal of Central South University，2013，20（4）：1122-1128.

［7］ ZHANG X，CHENG G D，ZHANG H.Theoretical predictionand numerical simulation of multi-cell square thin-walled structures［J］.Thin-Walled Structures，2006，44（11）：1185-1191.

［8］ ZHANG X，CHENG G D.A comparative study of energy absorption characteristics of foam-filled and multi-cell square columns［J］.International Journal of Impact Engineering，2007，34（11）：1739-1752.

［9］ KORMI K，WEBB D C，MONTAGUE P.Crash behavior of circular tubes with large side openings［J］.Int J Mech Sci，1993，35（3/4）：193-208.

［10］SAHU S K，DATTA P K.Dynamic stability of curved panels with cutouts［J］.J Sound Vib，2002，251（4）：683-96.

［11］SAHU S K，DATTA P K.Dynamic stability of laminated composite curved panels with cutouts［J］.J Eng Mech ASCE，2003，1245-53.

［12］KREMER T，SCHURMANN H.Buckling of tension-loaded thin-walledcompositeplateswithcut-outs［J］.Composites Science and Technology，2008，68（1）：90-97.

［13］KRAUSS C A，LAANANEN D H.A parametric study of crush initiators for a thin-walled tube［J］.Int J Vehicle Des，1994，15（3/5）：385-401.

［14］LEE S，HAHN C，RHEE M，OH J.Effect of triggering on the energy absorption capacity of axially compressed aluminum tubes［J］.Mater Des，1999，20（1）：31-40.

［15］王祝堂，田荣璋.铝合金及其加工手册［M］.长沙：中南大学出版社，2005：251-262. WANG Zhu-tang，TIAN Rong-zhang.Aluminum alloy and processing manual［M］.Changsha：Central South University Press，2005：251-262.

［16］彭晓东，李玉兰，刘江.轻合金在汽车上的应用［J］.机械工程材料.1999，23（2）：1-5. PENG Xiao-dong，LI Yu-lan，LIU Jiang.The applications of light alloys to automotive industry［J］.Materials for Mechanical Engineering，1999，23（2）：1-5.

［17］LEE K S，SEO H K，YANG Y J，HWANG W C，IM K H，YANG I Y.Collapse behavior evaluation of hybrid thin-walled member by stacking condition［J］.Transactions of Nonferrous Metals Society of China，2011，21（11）：135-140.

［18］向东，傅定发，娄燕，王冠，李灿，李落星.Al-Mg-Si多胞截面型材准静态轴向压缩［J］.中国有色金属学报，2012，22（7）：1843-1854. XIANG Dong，FU Ding-fa，WANG Guan，LI Can，LI Luo-xing. Quasi-staticaxialcompressionof Al-Mg-Siprofileswith multi-cell section［J］.The Chinese Journal of Nonferrous Metals，2012，22（7）：1843-1854.

［19］ARNOLD B，ALTENHOF W.Experimental observations on the crush characteristics of AA6061 T4 and T6 structural square tubeswithandwithoutcirculardiscontinuities［J］.IntJ Crashworthiness，2004，9（1）：73-87.

［20］ARNOLD B，ALTENHOF W.Finite element modeling of the axial crushing of AA6061 T4 and T6 and AA6063 T5 structural square tubes with circular discontinuities［J］.SAE International，2005：11-26.

［21］GHAZIJAHANI T G，JIAO H，HOLLOWAY D.Structural behavior of shells with different cutouts under compression：An experimental study［J］.Journal of Constructional Steel Research，2015，105：129-137.

［22］QINGWU Cheng，WILLIAM ALTENHOF，LI Li.Experimental investigations on the crush behaviour of AA6061-T6 aluminum squaretubeswithdifferenttypesofthrough-hole discontinuities［J］.Thin-Walled Structures，2006，44：441-454.

［23］HAN Hai-peng，FARID T，NEIL P.Quasi-static and dynamic crushing behaviors of aluminum and steel tubes with a cutout［J］. Thin-Walled Structures，2007，45：283-300.

(编辑王超)

Effect of cut-outs on axial collapse behaviors of aluminum with thin-walled structure

WANG Guan1，2，LIU Zhi-wen2，XU Cong-chang2，LI Luo-xing2
（1.College of Mechanical and Vehicle Engineering，Ningxia University，Yinchuan 750021，China；2.State Key Laboratory ofAdvanced Design and Manufacture for Vehicle Body，Hunan University，Changsha 410082，China）

The effect of cut-outs on deformation behaviors and energy absorption of 6063 aluminum with thin-walled structures will be investigated by quasi-static axial compression using WAW-E600 microcomputer controlled universal testing machine.The results show that the deformation mode of the aluminum extrusions is changed from Euler mode to Mixed mode after setting single line cut-outs on the specimen，and the energy absorption increases 26.78%.The deformation behavior is more stable and the peak force is lower than that of the complete sample during compression. The size and position of cutouts have very significant effects on axial collapse behaviors of aluminum thin-walled structure.The aluminum samples buckle under Euler mode with poor performance of deformation stability，loading force and energy absorption，because cut-outs locate in the middle of extrusions.Gradually changing size of cut-outs could leads that the compression behaviors become concertina mode.The aluminum extrusions collapse from top to bottom sequentially with steady load curve and excellent energy absorbing performance.Large cut-outs will introduce local buckling with shear deformation.The compression behavior is a new mode，which has stable load and successive collapse process.Based on the experimental data，the influence of cut-outs size on the critical force was studied.The relationship between critical force and inertia of the thin-walled structure was established by using linear regression.

thin-walled structure；cut-out；quasi-static compression；collapse behavior；deformation mode

Project（51475156）supported by the National Natural Science Foundation of China；Project（ZR1403）supported by Natural Science Funds of Ningxia University，China；Project（BQD2014018）supported by Research Starting Funds for Imported Talents of Ningxia University；Project（31515007）supported by Opening Foundation of State Key Laboratory ofAdvanced Design and Manufacture for Vehicle Body.

date:2015-03-31；Accepted date:2015-10-22

LI Luo-xing；Tel：+86-731-8821445；E-mail：llxly2000@163.com

TG146.21

A

1004-0609（2016）-03-0494-13

国家自然科学基金面上资助项目（51475156）；宁夏大学自然科学研究基金资助项目（ZR1403）；宁夏大学人才引进科研启动基金资助项目（BQD2014018）；湖南大学汽车车身先进设计制造国家重点实验室开放基金资助项目（31515007）

2015-03-31；

2015-10-22

李落星，教授，博士；电话：0731-8821445；E-mail：llxly2000@163.com